Управление пространственным движением геостационарного спутника связи в режиме длительной консервации

Первые попытки создания низкоорбитальных спутниковых систем связи (Teledesic, Iridium, Globalstar) потерпели крах в начале 2000 гг. в основном из-за экономических факторов. В настоящее время эта идея настойчиво навязывается в связи с возросшими требованиями к глобальности, скорости и объемам информационного обмена. В различных странах уже приступили к реализации таких систем, состоящих из тысяч мини-спутников связи на низких орбитах высотой от 500 до 1600 км, именно систем OneWeb (Великобритания), LeoSal, Boeing NGSO, StarLink (США), Telesat LEO (Канада), LinkSure Swarm (Китай) и др.

Достойный ответ традиционной космической связи [1], рис. 1, на основе геостационарных платформ противостоит этим вызовам. Такие платформы собираются на геостационарной

Рис. 1. Российский ГСС Экспресс-АМ5/АМ6

орбите (ГСО) космическими роботами-манипуляторами (КРМ) [2] из сменных и пополняемых компонентов, а затем регулярно обслуживаются КРМ в течение нескольких десятилетий.

Современные геостационарные спутники связи (ГСС) обычно имеют гарантированный срок активного существования (САС) 15 лет.

При продлении срока службы такого спутника важнейшей является проблема дозаправки топливом его электрореактивных двигательных установок (ЭДУ), например, с помощью смены соответствующих топливных баков. Баки, заправленные топливом, в течение примерно 4 месяцев должны доставляться космическим роботом по комбинированной схеме его выведения в окрестность точки стояния ГСС на ГСО. Однако из-за технических и организационно-технических рисков такое выведение КРМ с топливными баками может задержаться на несколько месяцев, поэтому в проектах перспективных геостационарных информационных платформ предусмотрен режим консервации ГСС с допустимой длительностью не менее 1 года.

Сущность режима длительной консервации заключается в пассивном полёте ГСС с обеспе- чением положительного среднего баланса его системы электроснабжения и эпизодическим включением его системы управления движением (СУД) для удержания ГСС в окрестности заданной точки его стояния на ГСО.

В статье кратко представляются разработанная стратегия управления пространственным движением ГСС в режиме длительной консервации и некоторые результаты компьютерной имитации этого режима для ГСС с крупногабаритными панелями солнечных батарей (СБ).

ПРЕДСТАВЛЕНИЕ ЗАДАЧИ

Инерциальными системами координат (ИСК), используемыми для описания пространственного движения КА, являются геоцентрическая экваториальная система координат (СК) I _⊕ (O _⊕ X_e^I Y_e^IZ^I_e ) и солнечно-эклиптическая СК I s (O s X s ^IY s ^IZ s ^I) , рис. 2.

Начало ИСК I⊕ расположено в центре Земли O ⊕ , ось XIe направлена в точку весеннего равноденствия ϒ , а ось ZeI – на Северный полюс мира PN по оси суточного вращения Земли с угловой скоростью ωe = ω⊕ . ИСК I s имеет начало в центре Солнца Os, её ось XsI также направлена в точку ϒ , а оси YsI и ZsI получаются поворотом соответствующих осей YeI , Z eI на угол εe относительно оси XIe (XsI ) . Угол εe между плоскостями земного экватора XeI O⊕YeI и эклиптики XsI OsYsI равен 0.41015234 рад (23.44 град), см. рис. 2. В ИСК I⊕ орт es направления из центра Солнца к центру Земли имеет вид e{(t) = [-£е]1[-р s(t)]3 {1,0,0}, где ρs(t)=ρs0+ωs(t-t0), ρs0=ρs(t0), t0 – некоторый начальный момент времени, tos = 0.19965 -10 6 с–1– средняя угловая скорость обращения Земли вокруг Солнца в плоскости эклиптики за тропический год (365.2422 средних солнечных суток). Здесь и далее используются общепринятые обо-значе~ния {⋅} = col(⋅), [⋅] = line(⋅), 〈⋅ ,⋅〉 ,(⋅)t, [⋅× ] и °, ‘ для векторов, матриц и кватернионов, матрицы [α] i элементарного поворота вокруг i -ой оси на угол α , а также i = 1,2,3 ≡ 1÷3 = x, y, z; Cα ≡cosα, Sα ≡sinα .

Астрономическая долгота Солнца λ _s , которая определяется в ИСК I _⊕ как угол между направлением на точку весны ϒ и ортом s = - e _s направления от центра Земли к центру Солнца, вычисляется по формуле λ _s( t ) = π + ρ _s( t ) .

Плоскость орбиты КА в ИСК определяют долгота восходящего узла Ω_^ и наклонение i _^ , рис. 3. Положение центра масс КА на эллиптической орбите с эксцентриситетом e определяется вектором r ( t ) и истинной аномалией ν ( t ) , отсчитываемой от перигелия орбиты π , который находится на угловом расстоянии ω_π от её восходящего узла в направлении движении центра масс (ЦМ).

Орбитальная система координат (ОСК) O (Oxoyozo) с началом в центре масс КА O и ooo ортами r , τ , n имеет следующие направления осей и ортов: ось Oxo направлена по ра-диали – орту r o вектора r^(t) , ось Ozo – по орту нормали no к плоскости орбиты, а ось Oyo с ортом трансверсали τo дополняет ОСК до правой ортогональной – принадлежит плоскости орбиты, перпендикулярна оси Oxo и направлена в сторону орбитального движения ЦМ спутника, см. рис. 3. Вектор угловой скорости ωo орбитального движения ЦМ КА определяется как too = ©°( t )n° = V (t )no.

Используются связная с корпусом КА система координат (ССК) B (O xyz ) (body) с ортами b _i , i = 1,2,3 ≡ 1 ÷ 3 ≡ x , y , z , которые направлены по соответствующим осям ССК, и центральная связанная система координат (ЦССК) B ^c (O x ^c y ^c z ^c) с ортами b _i ^c , направленными по главным центральным осям тензора инерции J = || J || спутника. Ориентация ЦССК B c в ССК B определяется ортогональной матрицей V _b ^c ≡ V ^c = [ v _i ^c ] направляющих косинусов координатного перехода, составленной из норми-

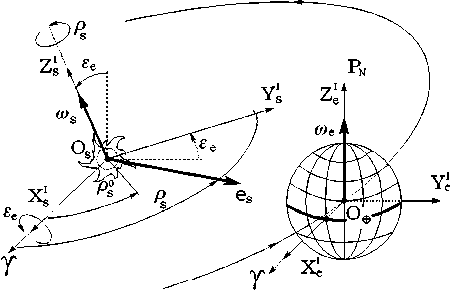
Рис. 2. Инерциальные СК и орбита Земли

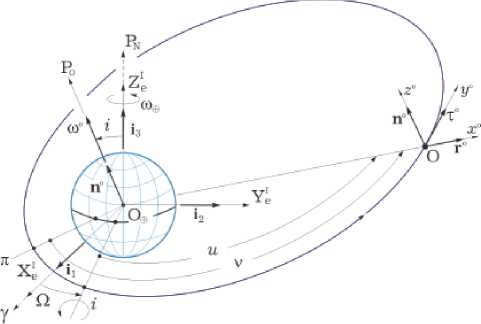
Рис. 3. Орбита КА и орбитальная СК

рованных собственных векторов v _i ^c матрицы инерции J , а также кватернионом Λ ^c _b ≡ Λ ^c . В центральной связанной системе координат тензор инерции спутника имеет диагональное представление J ^c = diag( J_i ^c ) и вычисляется по явному соотношению J ^c = ( V ^c ) ^t JV ^c . Ориентация ЦССК в ОСК определяется углами φ₁ ^c , φ ^c 2 и φ ^c ₃ в последовательности 132.

Ориентация ССК B в ИСК I _⊕ определяется кватернионом Л , = Л = ( Х₀,Х ) , где Х = { X i }, а в ОСК – углами рыскания φ ₁ = ψ , крена φ ₂ = ϕ и тангажа φ ₃ = θ в последовательности 132, а также матрицей направляющих косинусов C ^b _o ≡ C ^o = [ φ ₂]₂ [ φ ₃]₃ [ φ ₁]₁ координатного перехода от ОСК к ССК и кватернионом Λ ^b _o ≡ Λ ^o .

Связанная с панелями солнечных батарей (СБ) система координат (РСК) P (O ^p x ^p y ^p z ^p ) определяется так: ось O ^p z ^p и орт p 3 совпадают по направлению с осью O z и ортом b ₃ ССК, ось O^p x ^p и орт ^p 1 направлены по нормали n ^p к плоскости фотоэлементов СБ, а ось O ^p y ^p с ортом ^p 2 дополняют РСК до правой ортогональной. Угловое положение панелей СБ относительно ССК определяется углом γ их поворота вокруг оси O z ССК. В парковом положении СБ угол γ = 0 , когда направления осей РСК и ССК совпадают, см. рис. 4, где ССК O xyz спутника также совпадает с ОСК.

В СУД космического аппарата (КА) на ГСО применяются исполнительные органы в виде кластера двигателей-маховиков (ДМ) с цифровым управлением и ЭДУ на основе как плазменных, так и каталитических электрореактивных двигателей (ЭРД), а также электромеханический привод панелей СБ. В штатном режиме работы ГСС измерение кинематических параметров его движения выполняется бесплатформенной инерциальной навигационной системой (БИНС)

с коррекцией сигналами от навигационных спутников GPS/ ГЛОНАСС и звездных датчиков, ГСС стабилизируется в ОСК кластером ДМ, когда электрические оси его приёмно-передающих антенн, параллельные оси O x ССК, направлены в надир, а нормаль n ^p к плоскости фотоэлементов СБ регулярно наводится на Солнце с помощью электромеханического привода, см. рис. 4.

Диагональные элементы J_ii тензора инерции J = || J у || представляют моменты инерции КА относительно осей его ССК B (O xyz ) , именно J x = J _п, J y = J ₂₂ и J z = J ₃₃. Особенность стандартно применяемой компоновки конструкции ГСС заключается в соотношении J_y >  J_x >  J_z , что в штатном режиме приводит к проблемам гравитационной устойчивости углового положения ГСС в ОСК. Естественно эта особенность проявляется и для главных центральных моментов инерции J _i ^c спутника, именно в виде J ^c _y >  J_x ^c >  J_z ^c .

При пассивном полёте ГСС его угловое движение в ОСК в основном зависит от изменений вектора M ^s = { M_i ^s } моментов сил солнечного давления (ССД) и вектора M ^g = { M_i ^g } гравитационных моментов, обусловленных влиянием гравитационных полей Земли, Луны и Солнца. Задача состоит в разработке стратегии управления пространственным движением ГСС в режиме длительной консервации и апробации этой стратегии на основе методов компьютерной имитации.

СТРАТЕГИЯ КОНСЕРВАЦИИ

Разработанная стратегия основана на следующих последовательно выполняемых действиях.

• 1.    При штатной ориентации ГСС в ОСК приведение панелей СБ в парковое положение, когда угол γ = 0 , см. рис. 5;

• 2.    Разворот корпуса ГСС в ОСК в положение, когда ось O y ^c его ЦССК с ортом b ^c ₂ и макси-

  

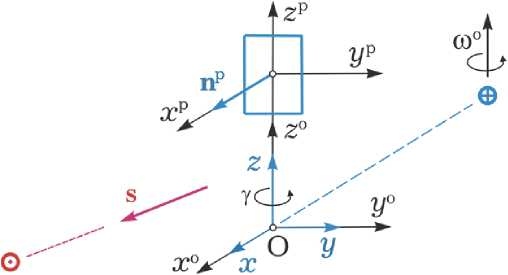
  Рис. 4. ОСК , ССК и РСК в штатном режиме

  
  
  

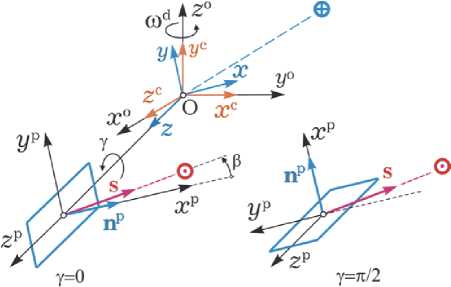
  Рис. 5. ОСК, ССК и РСК в режиме консервации

  
  

• 3.    Разгон вращения корпуса ГСС вокруг оси O y ^c , расположенной вблизи орта нормали n ^o к плоскости орбиты. Такой разгон до заданной скорости вращения ω ^d (см. рис. 5) с последующей стабилизацией выполняется кластером ДМ по сигналам эталонной модели наведения.

• 4.    Торможение роторов ДМ и стабилизация вращения корпуса ГСС с заданной скоростью с помощью ЭДУ на основе каталитических ЭРД при широтно-импульсной модуляции (ШИМ) их тяги.

• 5.    Выключение СУД и пассивный полёт ГСС, стабилизированного вращением [5], на временном интервале длительностью до 3 месяцев. Такие интервалы далее могут повторяться при кратковременном включении СУД для коррекции орбиты ГСС и возвращения его расположения в окрестность заданной точки стояния на ГСО.

мальным главным центральным моментом инерции J_y ^c направлена по оси O z ^o – по орту нормали n ^o к плоскости орбиты, а ось O z ^c ЦССК с ортом b ^c ₃ и минимальным главным центральным моментом инерции J_z ^c – по орту радиали r ^o , см. рис. 5. Пусть требуемое угловое положение ГСС задаётся кватернионом Λ ^d . Тогда погрешность ориентации ССК O xyz определяется кватернионом Е = ( e ₀ , е ) = Л ^d ° Л при векторе e = { e_i } , которому соответствуют матрица ошибки ориентации C ^e = I ₃ - 2[ e × ] Q _e ^t , где матрица Q _e = I ₃ e ₀ + [ e × ] , вектор модифицированных параметров Родрига (МПР)

С ^е = { о е } = е /(1 + e ₀ ) = е ^еtg( Ф ^е/4) с ортом e ^e оси Эйлера и углом Φ ^e собственного поворота, а также вектор угловой погрешности 5ф = {5ф i } = {4 о е } . Вектор ошибки δ ω ( t ) ≡ ω ^e ( t ) по угловой скорости вычисляется на основе соотношения ω ^e = ω - C ^e ω ^o ( t ) . Данный разворот выполняется с помощью кластера ДМ и эталонной модели наведения для вектора МПР [3, 4].

РЕЗУЛЬТАТЫ ИМИТАЦИИ

"15800 - 200 - 20" J =ЫУ\\= - 200 21000 0 _ - 20 0 6100 в стандартной размерности при значении угла γ = 0. При этом предполагалось, что ГСС имеет две крупногабаритные панели СБ площадью 40 м2 каждая, т.е. суммарная площадь панелей составляет 80 м2. В ЦССК указанный тензор инерции спутника имеет диагональное представление

J ^с = diag(16099,20808,5991) .

Компьютерная имитация моментов ССД выполнялась по известным аналитическим соотношениям с учетом различий в значениях коэффициентов отражения и поглощения светового потока для основной и тыльной сторон панелей СБ.

На рис. 6 приведены изменения углов рыскания φ ₁ , крена φ ₂ и тангажа φ ₃ в последовательности 132, а также угла Φ ^e при развороте ГСС на интервале времени t е [0,940] с в его гравитационно-устойчивое положение в орбитальной системе координат, а рис. 7 представляет управляющие моменты всех четырех ДМ при завершении такого разворота ГСС.

На рис. 8 и 9 приведены некоторые результаты имитации работы СУД в процессе подготовки ГСС к очередному пассивному полёту длительностью до 1 квартала (3 месяцев). Здесь в дополнении к рисункам 6 и 7 выполняются такие этапы:

• (i)    ∀ t ∈ [940,2944 ] c – угловая стабилизация ГСС в гравитационно-устойчивом положении, бортовая оценка возмущающих моментов ССД по доступным измерениям;

• (ii)    ∀ t ∈ [2944, 3944] c – разгон вращения ГСС по орту b ^c ₂ с помощью кластера ДМ до значения угловой скорости ω ^d = 24ω _e = 0.1 град/с (1 об/час) с последующей стабилизацией;

• (iii)    ∀ t ∈ [3944, 4944] c – сброс вектора кинетического момента кластера ДМ с помощью ЭДУ на основе восьми каталитических ЭРД с

  Исследовались динамические процессы при длительной консервации ГСС с массой 3500 кг и

  

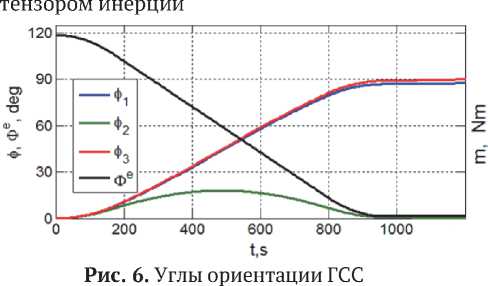
  при развороте в ОСК

  
  

  ШИМ их тяги;

  (iv) ∀ t ∈ [4944, 8444] c – стабилизация заданной угловой скорости ω ^d = 24ω _e с помощью

  
  
  

  800           900          1000

  t,s

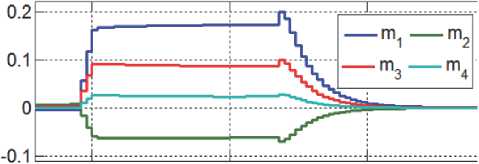
  Рис. 7. Моменты ДМ при завершении разворота ГСС

  
  
  

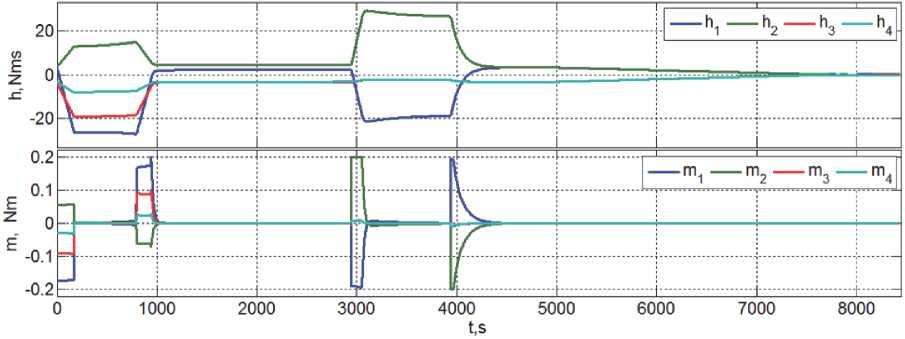
  Рис. 8. Кинетические и управляющие моменты ДМ при развороте ГСС и разгоне его вращения по орту b ^c ₂

  
  
  

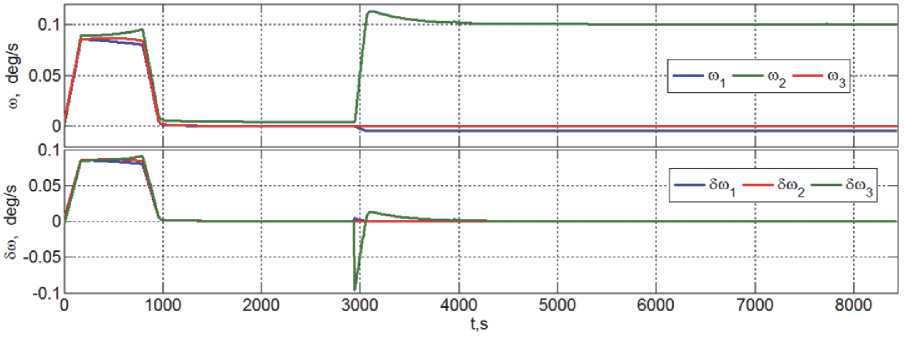
  Рис. 9. Векторы угловой скорости ^ω и ^{δ ω} при развороте ГСС в ОСК и разгоне его вращения по орту b ^c ₂

  
  

  ЭДУ на основе 8 каталитических ЭРД, остановка вращения всех 4 ДМ за счет естественных моментов сил сухого трения; выключение СУД при t = 8444 с.

Исследованы динамические процессы консервации ГСС на всех четырёх сезонных участках его пассивного полёта длительностью по 96 суток, именно по ± 48 суток относительно центров этих участков в особые даты 2021 года:

день весеннего равноденствия 20 марта, когда направление на Солнце переходит из южного полушария небесной сферы в северное;

день летнего солнцестояния 21 июня, когда достигается наибольшее отклонение направления на Солнце от небесного экватора в северном полушарии небесной сферы;

день осеннего равноденствия 23 сентября, когда направление на Солнце переходит из северного полушария небесной сферы в южное;

день зимнего солнцестояния 21 декабря, когда достигается наибольшее отклонение направления на Солнце от небесного экватора в южном полушарии небесной сферы.

На рис. 10 - 12 и 14 представлены некоторые результаты компьютерной имитации пассивного движения ГСС на участке «Весна» длительностью 96 суток начиная с 4 февраля 2021 г.

На рис. 10 приведены изменения компонентов вектора M ^s моментов ССД и вектора M ^g гравитационных моментов по поперечным осям O x и O z ССК вращающегося ГСС. Здесь необходимо отметить доминирующее влияние гравитационных моментов, что достигается тщательной балансировкой усредненных значений моментов ССД за счет реализации рациональных коэффициентов отражения и поглощения светового потока для тыльной стороны панелей СБ.

Рис. 11 представляет изменение углов ориентации орта b ^c ₂ в ОСК. Здесь ясно видно, что изменение этих углов относительно их номинальных значений не превышает 30 град.

Компоненты вектора δ φ углового отклонения ССК от заданного положения в ОСК по поперечным осям приведены на рис. 12. В другом масштабе изменения этих компонентов в течение 2 суток представлены на рис. 13, где име-

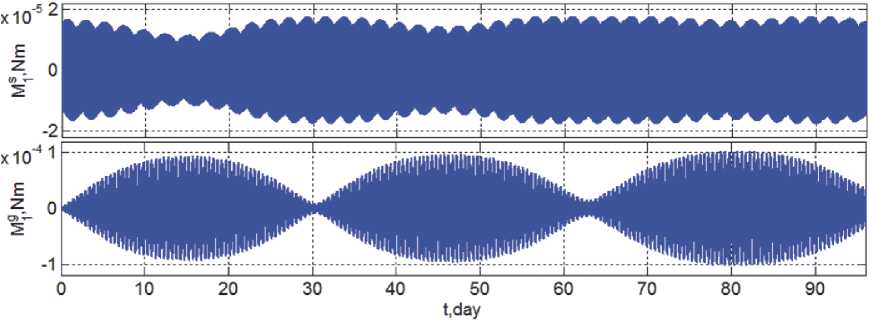
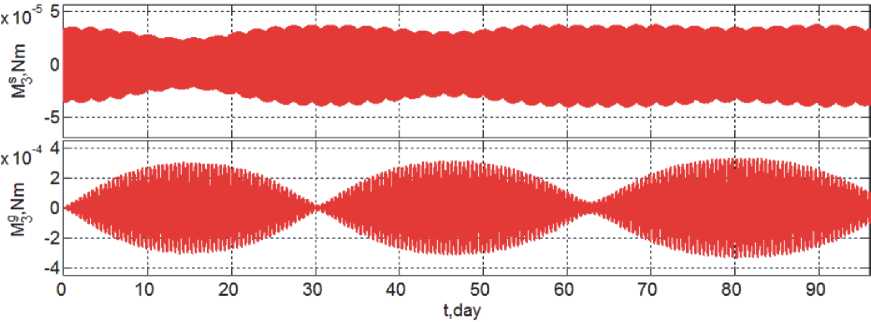
Рис. 10. Изменение возмущающих моментов по осям O x (синий цвет) и O z (красный цвет) ССК

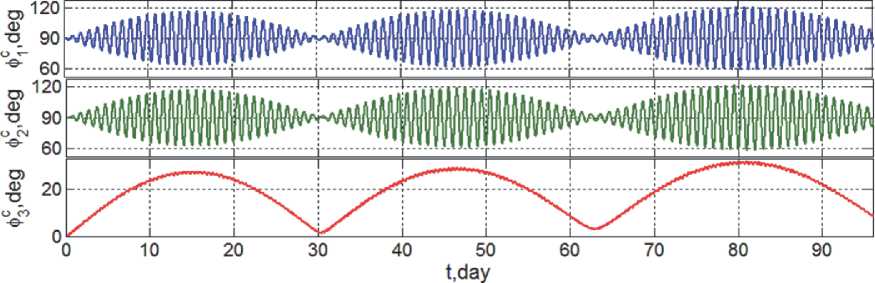
Рис. 11. Изменение углов ориентации орта b ^c ₂ относительно осей ОСК

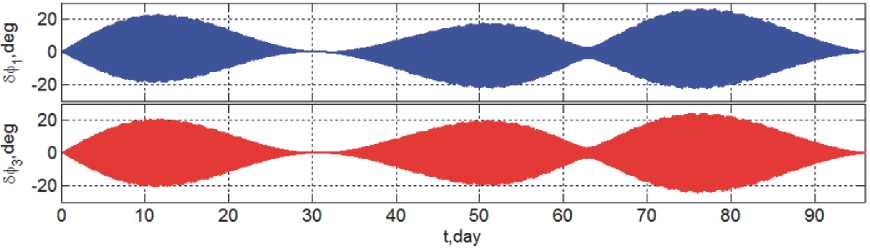
Рис. 12. Угловые отклонения ССК от заданного положения в ОСК по поперечным осям

ется также информация об изменении значений cos β , который определяет эффективность бортовой системы электроснабжения. Расчеты показали, что на участке « Весна » длительностью 96

суток среднее значение cos β равно 0.307.

На рис. 14 представлены изменения основных параметров орбиты ГСС на этом же участке « Весна » длительностью 96 суток. Здесь ясно видно,

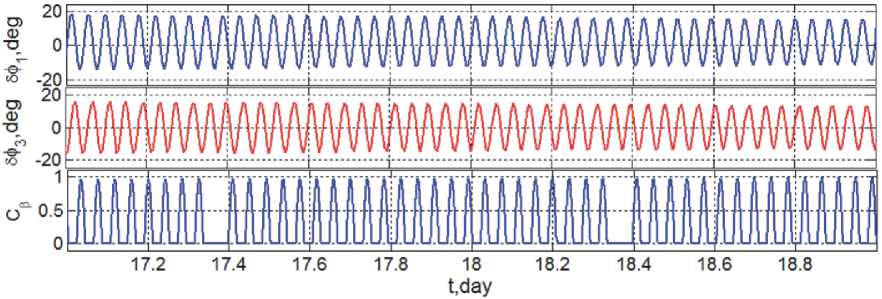
Рис. 13. Изменение ориентации ССК по поперечным осям и значений cos β в течение 2 суток

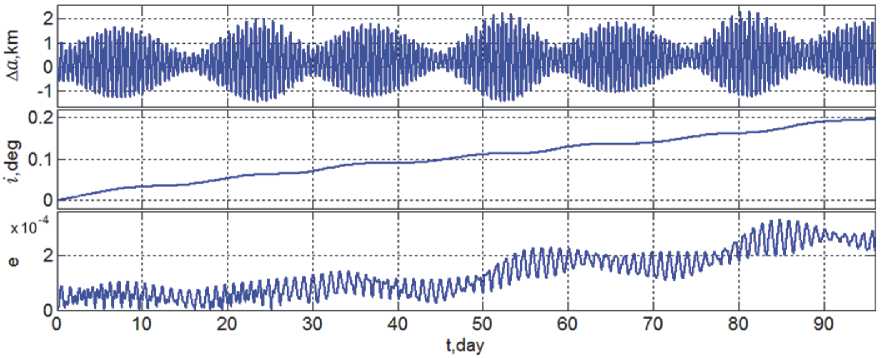
Рис. 14. Изменения большой полуоси, наклонения и эксцентриситета орбиты

что с возрастанием времени наклонение орбиты практически монотонно увеличивается. Именно это обстоятельство объясняет назначение четырёх сезонных участках пассивного полёта ГСС длительностью по 96 суток.

ЗАКЛЮЧЕНИЕ

Разработана стратегия управления пространственным движением геостационарного спутника связи в режиме длительной консервации, при необходимости с эпизодическим включением системы управления. Новизна этой стратегии заключается в разгоне и стабилизации вращения спутника вокруг главной центральной оси с наибольшим моментом инерции с помощью кластера четырёх реактивных двигателей-маховиков, а затем в пассивном гравитационно-устойчивом полёте вращающегося спутника длительностью до 1 квартала (3 месяцев). Представлены некоторые результаты компьютерной имитации такой консервации спутника связи с крупногабаритными панелями солнечных батарей.