Управление равновесием экологической среды региона в процессе развития экотуризма

В связи с ухудшением состояния окружающей среды во всех сферах мирового хозяйства идет поиск новых способов использования природных ресурсов. Главное, чем отличаются эти способы от предыдущих, - это уменьшение наносимого вреда природной среде в соответствии с концепцией устойчивого развития.

Туризм вошел в ХХІ столетие и стал глубоким социально-экономическим и политическим явлением, которое существенно влияет на мировое сообщество и экономику многих стран мира.

По оц енкам Всемирной туристической организации, экологический туризм входит в пять основных стратегических направлений развития туризма до 2020 года. Экологический туризм объединяет широкий спектр видов туризма, основанных на использовании природных ресурсов. Это пешеходный, горный, водный, спелеотуризм и др. Экологический туризм успешно развивается во многих странах мира и приносит им немалую прибыль, а учитывая то, что год от года наблюдается ухудшение экологической ситуации во многих традиционно рекреационных зонах мира из-за не контролированной чрезмерной концентрации туристов, усиливается заинтересованность экологическим туризмом.

Учитывая эти обстоятельства, можно считать экологический туризм целесообразным и необходимым элементом государственной концепции устойчивого развития туризма в перспективе.

Моделью сбалансированного использования природных ресурсов как важного принципа устойчивого развития экологического туризма является осуществление его на рекреационных территориях национальных природных парков, биосферных заповедников, региональных ландшафтных парков и заказников.

Основная цель данной работы – построить две модели экологического туризма, которые позволят определить зависимость изменения уровня загрязнения окружающей среды от количества экологических туров , проводимых на данной территории за единицу времени.

Задачи работы состоят в следующем:

• -    определить, применение какой из моделей наносит меньше вреда окружающей среде;

• -    определить, применение какой из моделей принесет большую прибыль;

• - провести графический анализ для каждой из моделей;

• -    по итогам проведенного исследования сделать общие выводы.

Прежде, чем переходить к построению модели необходимо сформулировать принципиальную идею её работы. Она заключается в следующем: будем строить циклическую модель системы, которая через определенные интервалы времени должна возвращаться в исходное состояние.

Введем неизвестные величины:

х=х(1) - уровень загрязнения окружающей среды на территории где проводится экологический туризм.

y=y(t) — количество экологических туров проведенных на данной территории к моменту времени t.

Так как идея состоит в том, что модель имеет циклический вид, то можно сделать следующее предположение: график функции, описывающей зависимость между х и у, имеет вид замкнутой кривой с центром в I четверти координатной плоскости. Центр находится в I четверти, так как значения принимаемые х и у должны быть больше 0. Рассмотрим точки A и B (рис.1). В этих точках у принимает свое наибольшее и наименьшее значение. Вспоминая о том, что у есть функция от времени, можно сказать, что в точках A и B первая производная по времени от у (далее у') , равна 0. Также отметим, что проходя через эти точки, производная меняет свой знак на противоположный.

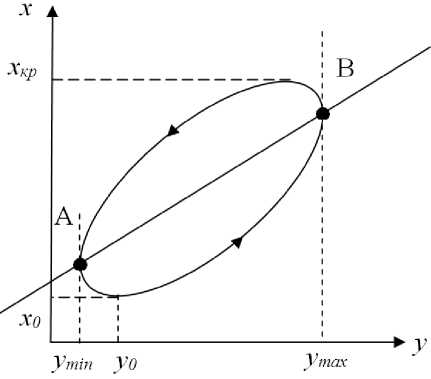
Рисунок1 . Предполагаемая зависимость уровня загрязнения окружающей среды от количества экологических туров

В начальный момент времени уровень загрязнения минимальный, обозначим его как х₀ . Он не может быть равен 0, так как прежде чем начать организовывать экологические туры, необходимо создать инфраструктуру на выбранной территории, что, в свою очередь, нанесет вред окружающей среде. Этот вред мы и будем считать начальным уровнем загрязнения или х₀ .

Учитывая все выше сказанное, можно сделать вывод о том, как будет вести себя система. В начальный момент времени имеем уровень загрязнения х0 и какое-то начальное значение у0, далее начинаем увеличивать количество туров за единицу времени. Это приводит к росту уровня загрязнения. После того, как у достигает максимального значения (точка B), количество туров за единицу времени начинает снижаться. Несмотря на это, уровень загрязнения ещё некоторое время продолжает расти, пока не достигнет хкр, после чего начнет уменьшаться. Затем в точке A у принимает минимальное значение и опять начинает увеличиваться. Уровень загрязнения падает до начального уровня и вновь начинает расти. Цикл повторяется.

Составим уравнение для у' . Проведем прямую через точки A и B . Данная прямая описывается уравнением х=ку+с, где к и c неизвестные коэффициенты. Из рис. 1. видно что, если уровень загрязнения х в определенный момент времени меньше, чем значение функции х=ку+с , то у возрастает с течением времени, то есть у' > 0, если же уровень загрязнения больше, то убывает: у' < 0.

Исходя из выше сказанного, можно составить уравнение для у':

у' = п ( ку + c - х ),               (1)

где п - некоторый коэффициент пропорциональности.

Теперь составим уравнение для х'. Скорость изменения уровня загрязнения есть разность между скоростью восстановления окружающей среды и скоростью её загрязнения. Скорость восстановления окружающей среды при возникающих отклонениях от равновесного состояния пропорциональна величине отклонения, то есть пропорциональна самому уровню загрязнения х. [2] Коэффициент пропорциональности (обозначим его через а) есть коэффициент релаксации, который зависит от уровня возмущения биоты (биота - совокупность видов живых организмов, объединенных общей областью распространения). Так как мы строим модель экологического туризма, то будем считать, что возмущение биоты минимально и не меняется с течением времени.

Следовательно, коэффициент пропорциональности (релаксации) также будем считать постоянным (однако, при более глубоком изучении данного вопроса можно принять данный коэффициент переменным). Скорость загрязнения окружающей среды можно записать произведением Ьу, где b - вред, наносимый од ним туром.

Таким образом, получаем систему диф ференциальных уравнений:

х' = -ах +

by

у' = пку + пс -пх

экотуризма

Найдем точку покоя для данной системы уравнений. Для это приравняем x` и y` ну-

лю, тогда получим
0 = -ax + by	(3)
{ 0 = nky + nc -nx ,

Л = 0 ± iq . Исходя из этого, получим следу-1,2

ющее соотношение: nk = a.

Сделав замену Л = ± bjbn — a² , при

1,2

откуда x = ky + c {0 = - any - ac + by, (4) или

bn — a ² >  0 , получим решение системы:

X ( t ) = Y 1 e ² t y ⁽ t ) = у 2 e ^{z t}

= ac

y b-ak= bc b-ak

.

Мы нашли точку покоя,

которая имеет

координаты P

ac

bc

a - i

При Л 1 = i V bn — a ² имеем систему:

^ — ( a + i-Jbn — a 2 ) 7 1 + b y 2 = 0 (Ц)

—ny1 + (a — i V bn — a2 )y 2 = 0

Если первое уравнение умножить на ^rV bn - a ² , а второе на b , то получим одина-

b-ak;b-ak,"

Теперь определим тип Введем замену:

точки

покоя.

ковые уравнения, следовательно, одно из них можно вычеркнуть, например, второе.

Таким

образом

Y 1 = 1,

/=x+ibOk ac , у = у+т—т I b-ak следовательно из (2) получим,

a 1

y = + 1—У bn 2 bb

^^^^^^B

a ²

.

x = - a

- bc

x+k---

к

y= nk y+

b-ak

ac

+ b y+

ac

откуда

или

\

к

b-ak

+ nc - n

b-ak

“ bc

I x +-- b-ak

к

,

Аналогично

Y i = 1, Y 2 = a — i ¹ !ьй bb

x ' = — ax + by +

—

■ abc + abc b-ak

y = nky — dn + ...

nkac + ncb — ncak — nbc

... ⁺          b-ak

, (8)

для Л 2 = — bjbn — a²

—

a ² Частное решение

представлено формулами:

(        1        ^.

x 1

y ₁

,

x 2

y ₂

= a . . 1 r— — + i—\bn к b b

^^^^^^B

a ²

cos( bn

—

a

b

a - —

b

e

—V bn — a ² | ( cos( 4bn b 7

a ² 1 ) + i sin( V bn — a²1 )

—

a ²

a

—

i bn b

—

a ²

cos( bn

—

e - i

i—^bn — a ² | ( cos( Jbn b 7

a ² 1 ) — i sin( V bn — a²1 )

—

a ²

< x = - ax + by y = nky - nx

Решим систему (9) методом

,

Характеристический

многочлен

- a - Л   b

- n   nk - Л

= (Л + a)(Л - nk) +...

Эйлера.

равен ( x к к y 7=C1

Общее решение системы можно записать в виде:

cos

—

a21)

... + bn = Л ² + ( a - nk) Л + ( bn - ank ) откуда

a

—cos

к b

।n — a ² sin

sin

—

^Л 12

nk — a ± ( a — nk )² — 4 bn + 4 ank

получим + _C

a21)

[4] .

a .

—sin к b

।n — a ² cos

Так как модель циклична, то корни ха-

,

рактеристического многочлена имеют вид окончательное решение

Сделаем обратную замену и запишем

x ( t ) = C1 cos(V bn - a ² t ) + C ₂ sin(7 bn - a ² t ) + -b—

¹                   2    _______ b - ak

< y ( t ) = C 1 I a cos(V bn - a²t ) — 7 bn - a ² sin( 7 bn - a²t ) 1 + (15)

V ^{b b}                     . J

+ C — sin( \bn - a ² t ) — bbn - a ² cos( \bn - a ² t ) +-----

I ² V b             ' b                       J b - ak

Теперь, для того чтобы полученное решение можно было применить на практике, необходимо выразить неизвестные коэффициенты через известные величины. Ещё раз вспомним, какие данные нам известны:

a – коэффициент релаксации на рассматриваемой территории; b – ущерб окружающей среде, наносимый одним туром; x0 – начальный уровень загрязнения; xкр – критический уровень загрязнения. Коэффициенты c, n, k нам неиз- t ) + ...

/    ,(16)

вестны.

Возьмем первую производную x по времени, тогда получим x'=-C1 -Jbn - a2 sin (Vbn - a2i

... + C ₂ ^bn - a ² cos(7 bn - a²t

Известно, что в начальный момент времени t= 0 , значение x минимально, т.е. x’= 0 , следовательно: 0 = C ₂ ^bn - a ² , а значит C₂ = 0 .

Теперь найдем значение C1. Для этого сначала определим моменты времени, в которые x’=0: 0 = -C1 ^bn - a2 sin(7bn - a2t), так как Vbn - a2 > 0, а C1 ^ 0, то

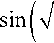
bn - a²t ) = 0, откуда

Vbn - a2 • t = n ■ l, где l eZ, следовательно, t = , П , где l eZ. V bn - a2

Исходя из предположения, что в нашей модели минимум и максимум x поочередно сменяют друг друга, заметим, что при l=0, x достигает своего минимума x0, следовательно при l=1, x достигнет своего максимума, т.е. xкр. Составим систему уравнений.

содержащие данные неизвестные:

ac _a bc _ a x о ⁺ x кр b - ak b" b - ak ~b 2   ^.

Теперь выразим Vbn - a2 . Для упроще ния восприятия расчетов введем ф = Vbn - a2 и запишем уравнение для y, учитывая введенные замены:

x0 хкр [ a                1

y ( t ) =          I cos( ф ■ t ) - ф sin( ф ■ t ) 1 + ...

• 2 V b          bJ

• ^{a (} x 0 ⁺ x кр )

... +

2 b

Так как всегда y ≥ 0, запишем и решим неравенство относительно φ

• —⁰---- кр- 1 ^a cos( ф ■ t ) - —ф sin( ф ■ t ) | + ...

• 2    V b          b J

a(x ₀ + x _KJ                        .

... + i °-----кр; >  0.

2 b

Перен есем второе слагаемое вправо и умножим обе части на          . Так как x 0 - Хкр x0 - xкр < 0, а b > 0, то все выражение меньше 0, следовательно, изменим знак неравенства на противоположный:

x _кп + x ₀

a cos( ф ■ t ) - ф sin( ф ■ t ) <  a —^р-----.      (20)

^x кр ^{- x} 0

Вынесем в левой части неравенства (20)

из скобки множитель ^a ² + ф ² :

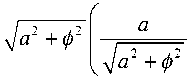
С08( ф ■ t ) -

ф

4 a ² + ф ²

sin( ф ■ t ) <

x кр

bc b - ak bc , н--------- b - ak

. ^x кр ^{+ x} 0

< a— ---.

^x кр ^{- x} 0

Так как

_ x 0 ^- x кр откуда C 1 = —-—- .

bc

Из этой же системы выразим        :

b - ak

a , ф

_V V a² + ф ² J V V a ² + ф ² ₇

то можно ска-

a зать, что          является косинусом некото-

7 a ² + ф ²

bC = ^x 0 ^{+ x} кр b - ak 2 .

Нет необходимости находить отдельно коэффициенты c, d, k, поэтому выразим через известные нам величины только выражения,

рого углa θ, a

ф a2 + ф2

синусом того же угла,

откуда:

7 a ² + ф ² (cos в cos( ф ■ t ) - sin 0 sin( ф ■ t )) < ....

экотуризма

x + x

... <  a -кр----0                           (22)

x кр ^{- x} 0

Выражение cos9cos(ф-1)-sin9sin(ф-1) является формулой косинуса суммы, сл едовательно, его можно свернуть в cos (9 + ф-1). Значения, которые принимает косинус, лежат в интервале от –1 до 1, поскольку выражение (22) верно при любых t, то в случае cos (9 + ф-1) = 1, можем записать:

гу— ^x кр ^{+ x} 0

^ a + ф < a—----, откуда xкр - x0

2 a  x _кр x ₀

ф < —---- xкр - x0

или

4bn - a²

< ² a 7 x ^ x 0

x _кр

x ₀

Принимая V bn - a² = — ^ ^{кр 0}

x кр - x 0

можно

записать окончательное решение с использованием только известных величин:

x ₀ x ( t ) =—

^^^^^^в

x кр cos

X Xn кр 0t

—

кр x 0

x 0 ⁺ x кр

y ( t ) = x ⁰

—

x кр

a cos b

x кр x 0 t

^: кр ^- x 0

2 a x _кр x ₀ sin

b ( x _кр

x 0 )

2 ax _кр x ₀ t x кр - x 0

a ^{( x} 0 ^{+ x} кр )

+-----—

L ^{2 b}. ,

Следующий шаг будет заключаться в том, чтобы найти уравнение фазовой кривой. Запишем ещё раз исходную систему уравнений.

-

2 nx ² ---+

ncx - C = 0 ,

а

значит

x` = -ax + by

{ y' = nky + nc - nx

x 1,2

—,

■ nc ±7 ( nc ) ² - 2 nC

.

Разделим первое уравнение на второе и сделаем замену nk = a , тогда получим ( ay + nc - nx ) dx + ( ax - by ) dy = 0     (25)

Пусть P = ay + nc –nx и Q = ax – by. Так как P` y = Q` x , то получим уравнение в полных дифференциалах. Решив его стандартным ме-

- n

Так как y должен быть больше или равен нулю , то дискриминант должен быть меньше или равен нулю, иначе мы получим два корня, и, следовательно, y сможет принимать отрицательные значения, что противоречит

тодом, получим nx2              by2

-    + ayx + ncx --= C .

Выразим неизвестные величины через

условиям задачи. Таким образом, запишем неравенство

2                             nc ²

( nc ) - 2 nC <  0, откуда C > —— .

2a xкрx0 известные. Т ак как bn- - a < —-----, то x кр - x0

nc ²

Пусть C = —— , тогда подставив n и c ,

< a ^{2   x} кр ^{+ x} 0

” ^b ( x кр ^{- x} 0 _v

получим C =

2 ax _кр x ₀

b ^{( x} кр ^{- x} 0 ⁾² '

bc     x 0 ⁺ x кр      ,

Вспоминая, что -----=------ и nk = b - ak 2

Теперь можно записать окончательное

уравнение фазовой кривой:

nbc    x о + xкр a, получим -----2 =------. Принимая bn - a2     2

bn - a ¹

4 a ² x _кр x ₀

^{( x} кр ^{- x} 0 ⁾²

и

a ² ( 5 р b I ^x кр

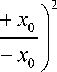
полу-

al ( 5p 2 b ( xкр by2

■0

x + ayx +

2 a ² x кр ² x 0 ²

^{2     b ( x} кр ^{- x} 0 ⁾²

² a ² x кр x 0 ⁽ x кр ⁺ x 0 ) ------------- 2---- x - .

^{b (} x кр - x 0 )

чим c = —кр—°- . Теперь найдем С , для этого в x кр ^{+ x} 0

формуле (26) приравняем y нулю, откуда

Полученное решение является уравнением кривой второго порядка. Несложно определить, какую именно кривую описывает данное уравнение. Для этого определим знаки ин-

вариантов A , D , I .

Если

nc ²

C =---, то

2,

A =

D =

n

—

a nc

2 n 2 c 2 b

n

—

a

a

b

—

nc

2 0

— C

2 a ² nc

a

2 b

—

^^^^^^в

bn ² c ² 8

+ ...

;

bn

I =

n

—

Z 1

^{п ( х} кр ^{— х} 0 )

a x _кр x ₀

f

2 a ² nc

a ²

^—т > ^0;

4 <  0;

2 b

a ^{( X} 0 ^{— X} кр ) ------— cos

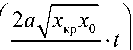
_V ^X кр ^{— X} 0

2 a  x _кр x ₀

+

+ a TyO

+ b V

sin

x 0 x _Кр      ² a^x кр ^X 0

+---- -cos —-----

² b V x кр ^{— X} 0

^X кр ^{— X} 0 ^{n (} x кр ^— x 0 )

a x _кр x ₀

+

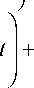
a ^{( X} 0 ^{+ X} кр )

2 b

Так как D >  0, а I A< 0, то наша кривая имеет вид эллипса [3] .

Исходя из полученных данных, можно определить количество туров проведенных за определенный интервал времени, и следовательно прибыль от них. Так как наша модель имеет циклический вид, то целесообразно в качестве интервала взять время, за которое система пройдет весь цикл и вернется с начальное

~     Пxкр состояние, то есть tц =---^

—

x ₀ )

.

a x _кр x ₀

Таким образом, количество туров, которое будет проведено за выбранный период, можно рассчитать по приближенной формуле:

dt =

, ^П ( x кр ^— x 0 ) a ^{( X} 0 ^{+ X} кр )

2 b

a x _кр x ₀

( X 0 — X кр ) 2 - ( ² a T^ -----, sin ------------

⁴ b V x кр x 0     V ^XKP ^{— X} 0

^{n (} x кр

—

• t

a ^{( X} 0 ^{+ X} кр ) ^П ( ^X KP ^{— X} 0 ) = ^{n ( X} кр ^{2 — X} 0 ²⁾

2 bax _кр x ₀       2 b x _кр x ₀

Теперь рассмотрим альтернативную модель той же системы. Предположим, что мы зафиксировали определенное количество туров проводимых за единицу времени. Другими словами y=const . Тогда поведение системы можно описать следующим образом. В начале мы будем иметь экспоненциальный рост уровня загрязнения, до тех пор пока он не достигнет критического уровня, после чего мы прекращаем туристическую деятельность и ждем, пока уровень загрязнения достигнет своего начального значения. Уменьшение также будет экспоненциальным. Так как значение y мы можем выбрать произвольно, то подберем его исходя из следующих соображений. У нас есть две модели, следовательно, необходимо произвести их сравнение по какому-либо признаку. В качестве признака возьмем прибыль, полученную за время, необходимое для прохождения первой системой полного цикла. Для этого определим количество туров, проведенных за этот период. Перейдем к построению второй модели.

Первый шаг будет заключаться в том, чтобы рассчитать время отсутствия туристической деятельности. То есть, то время, за кото- рое уровень загрязнения снизиться от критического до начального (минимального) уровня.

Имеем x '=- aX,                      (32)

откуда x = C • e—at                        (33)

Теперь найдем С при t=0, x = xкр. Очевидно, что С = xкр, тогда х = хкр • e—at. Теперь можно найти время отсутствия туризма . Если ln x0

• _{— t}                 X

x ₀ = x • e a , то t =--- . Обозначим его t _от с .

р a

Второй шаг заключается в нахождении такого значения y , которое будет удовлетворять нашим условиям построения альтернативной модели. Не забывая о том, что y=const , решим уравнение:

х '= — ax + by                 (34)

Представим x как произведение двух функций u и v, тогда

• u ' v + u ( v ' + av ) — by = 0        (35)

Подберем функцию v так, чтобы выражение v '+av было равно 0, откуда v = e ^{— at}.

Имеем дифференциальное уравнение с разделяющимися переменными:

u '• e^{— at} = by                       (36)

решение, которого будет иметь вид x = by + C • e-at               (37)

a

В начальный момент времени уровень загрязнения равен    x0,    следовательно, x0 = — + C , а значит, C = x0 - —. aa

Таким образом, x = x0 • e-at + by(1 - e-at)         (38)

a

экотуризма

Теперь мы можем определить, какое количество туров может быть проведено, используя данную модель: Z 2 = y • t _р , то есть

Z 2

кр

I^{- x} 0 )

-+ln - x L

a

x кр

—

^x 0 • ^e

кр

кр

-+ln ^0-

b

1 - e

кр

п(xкр - x0 ) +   xкр a xкрx0      a

Из уравнений первой модели мы знаем, что время, необходимое для прохождения си- _ - . . .      .         ,   ^П(^x кр ^{- x} 0 )

стемой полного цикла равно t _ц =---.      .

a x _кр x ₀

Время, которое требуется для того, чтобы уро-

вень загрязнения поднялся с начального уровня до критического обозначим t р .

Имеем

b

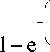
п

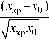
+ ln ^0- x кр

t — t — t_ _ р ц отс

ln ^{x 0}

п(xкр - x0 ) +   xкр a xкрx0       a

Теперь мы можем найти значение y и

записать окончательное решение, исходя из заданных условий.

Поскольку, xкр = x0 • e-atр + by (1 - e-atр )        (40)

то

_ a ( ^x кр ^{- x} 0 • e ^- at р )

y = b (1 - e-atр)    , а значит согласно формуле (38)

x = x 0

• e

x кр

—

x ₀

•

e

.^- at р

- at

1 - e ^р

( 1 - e ^- at )

После подстановке а и t p , получим

П x- - x

\ кр x ⁰ / + in ^x 0

x кр x 0       x кр

f                             11

П x  - x,. I _v

- 1 кр   ⁰¹ + ln A

V x p ^x 0

Xкр - x0 • e

1+(x0 -xкр )• e

при постоянном значении количества туров, проводимых за единицу времени, равном f                Г n ( xкр - x0 )+in x0 p

y »

b 1 - e

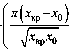
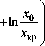
Сравним наши модели. Для этого сделаем следующие шаги:

• 1.    Построим график функции, показывающий зависимость y от x , для первой модели.

• 2.    Построим для обеих моделей графики функции, показывающих изменения уровня загрязнения от времени.

• 3.    Найдем количество туров, проведенных за одно и то же время. В качестве интервала возьмем время прохождения первой моделью полного цикла.

На первом шаге зададим значения необходимым нам параметрам:

x 0 = 1% , x кр = 14%, a= 0,1 ¹_месяц , b= 0,1%_туры.

Запишем параметрические уравнения первой модели:

x ( t ) = - 6,5cos ( 0,057 • t ) + 7,5

< _(A        cos ( 0,057 • t ) - ...     Y₇ ,,(46)

y ( t ) = - 6,5     ;     . Л a + 7,5

1 ... - 0,57sin ( 0,057 • t ) J графическое изображение, которой представлено на рис.2

Теперь перейдем ко второму шагу. Для первой модели:

x ( t ) = - 6,5cos ( 0,057 • t ) + 7,5, для второй модели x = 14 - 13 • e ^{- 0,1v} - при наличии туристической         деятельности         и

- 0,1 ^ t + 8,27

x = 14 • e           - при её отсутствии.

Из рис.3 видно, что в случае второй модели (сплошная линия) уровень загрязнения долгое время находится близко к критическому значению. Это явно более негативно влияет на окружающую среду, чем, если бы мы использовали первую модель (пунктирная линия).

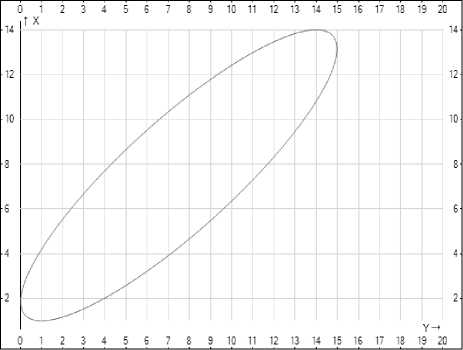
Рисунок 2. Зависимость количества экологических туров от уровня загрязнения окружающей среды

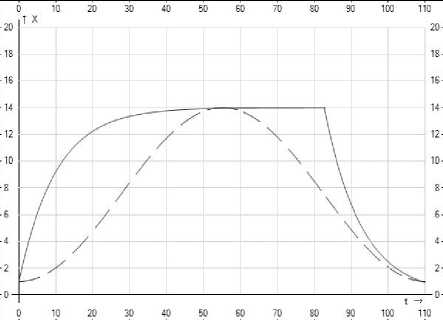
Рисунок 3. Зависимость уровня загрязнения окружающей среды от времени

Наконец, перейдем к третьему шагу. Время, за которое первая модель пройдет весь цикл равно t _ц = 109,2 месяца . Количество туров проведенных за это время, равно: Z 1 =819 туров для первой модели и Z 2 =1220 туров для второй модели (смотри формулы 31, 45).

Таким образом, можно сказать, что использование второй модели даст большую прибыль.

В данном исследовании мы составили две различные между собой модели экологического туризма. Цель их создания заключалась в том, чтобы показать, как изменяется уровень загрязнения окружающий среды в зависимости от выбранного нами способа организации туризма, а также, какую прибыль может принести применение каждой из них.

Использование первой из рассматриваемых моделей приносит меньшую прибыль, однако в этом случае наносится меньший вред окружающей среде. Применение второй модели позволит получить больше прибыли, но и вред от такого выбора будет больше. Такой вывод можно сделать на основании ранее построенного графика.

В жизни, как правило, выбор падает на модель, которая приносит большую прибыль. Однако, на наш взгляд, использование первой модели целесообразнее по нескольким причинам:

• -    во-первых, вред наносимый окружающей среде меньше;

• -    во-вторых, рост уровня загрязнения происходит более плавно, что позволяет сохранять способность окружающей среды к самовосстановлению даже через очень длительное время;

• -    в-третьих, так как окружающая среда находиться в более хорошем состоянии, то можно устанавливать более высокие цены на туры, что в свою очередь позволит приблизиться к показателям прибыли второй модели;

Если учесть все вышесказанное, то можно сделать вывод: при примерно одинаковых показателях доходности следует выбирать ту модель, которая наносит меньшей вред окружающей среде, то есть первую.