Управление системой нелинейно связанных перевернутых маятников

Теория колебаний нелинейных систем широко применяется при моделировании различных физических явлений: колебания молекул в жидкостях и твердых телах, электрических цепях, состоящих из нескольких взаимосвязанных контуров и т.д. [1] В таких системах реализуются разнообразные дисперсионные зависимости, на основе которых исследуется распространение волн в нелинейных средах. Подавляющее большинство моделей таких систем основывается на законах движения простейших связанных осцилляторов и их цепочек, динамика которых формализуется посредством как линейных, так и нелинейных уравнений. В большинстве подобных задач рассматриваются колебания маятников, у которых нулевое положение является устойчивым [2-4]. Подробный обзор последних результатов в этой области приведен, например, в [5].

В то же время в ряде практически важных задач (например, колебания атомов в телах с большой температурой, проблема стабилизации плазмы) нулевое положение неустойчиво. В связи с этим отметим классическую задачу стабилизации верхнего положения обратного маятника [6]. При решении этой задачи основное внимание уделяется проблеме стабилизации неустойчивого положения равновесия маятника путем движений нижней точки крепления. Этой проблеме посвящено огромное количество публикаций, достаточно подробный обзор которых содержится в [7]. Особенностью жесткого маятника с осциллирующим креплением является возможность динамической стабилизации его верхнего положения. Задача стабилизации ма-– 281 – ятника с помощью вертикальных осцилляций точки крепления хорошо изучена и сводится к уравнению Матье [8]. Теоретическое объяснение этого явления было сделано Стефенсоном в 1908 г. [9]. Физическое объяснение динамической стабилизации перевернутого маятника вертикальными осцилляциями точки крепления (с помощью управления по обратной связи) было предложено академиком П.Л. Капицей в 1951 г., выполнившим детальное экспериментальное исследование этого явления [10]. Также отметим работы, в которых стабилизация верхнего неустойчивого положения осуществлялась посредством гистерезисного управления [11-14].

Постановка задачи

В настоящей работе рассматривается система, состоящая из двух перевернутых маятников массами т 1 и m 2 , связанных между собой пружиной с жесткостью к . Основная задача работы заключается в формировании такого закона управления горизонтальным движением точки крепления, при котором фазовые координаты системы остаются в ограниченной области фазового пространства. Иными словами, речь идет об условиях, накладываемых на параметры системы и управление, обеспечивающих диссипативность системы. Рассмотрим решение данной задачи для различных вариантов управления рассматриваемой системой (управление может быть приложено как к одному маятнику системы, так и к системе в целом) и в случае линейной и нелинейной жесткости системы.

Случай управления одним маятником

Рассмотрим систему с линейной жесткостью и управлением, приложенным к одному из маятников. Ее физическая модель представлена на рис. 1.

Задачу стабилизации будем решать в предположении, что тележка не имеет массы и движется без трения, а управляющее воздействие сообщает ей ускорение и . В этом случае уравнения динамики системы имеют вид

J 1 ф , = m 1 gl 1 sin ф , + kh ² ( sin ф₂ - sin ф , ) - u <

J 2 ф₂ = m 2 gl ₂ sin ф₂ - kh ² ( sin ф₂ - sin ф , )

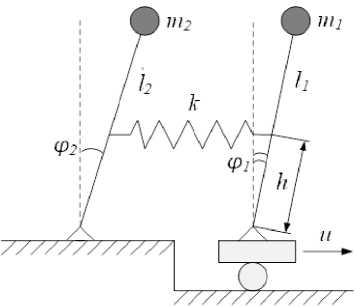
Рис. 1. Физическая модель связанных маятников

Fig. 1. Physical model of coupled pendulums

где ф 1 , ф ₂ - углы отклонения маятников от вертикального положения. Предполагая отклонения от нулевого положения малыми, линеаризуем уравнения динамики. Тогда уравнения (1) примут вид

<Р ] _	f mxglx kh 2)      k h 2       mxl 2 T1 T |ф ] + T Ф 2 V У JJ   J   J
1-	<               2 Л           2                ■                                                  (2) m2gl2 kh 2 |       khh
ф 2 _	J      J  |ф 2 ' J ф 1 i и 2        и 2 1         и 2

Для дальнейшего рассмотрения систему (2) удобно представить в форме четырех уравнений первого порядка. Введем переменные: z 1 = ф 1 , z 2 = ф 1 , z 3 = ф ₂, z 4 = ф ₂ и обозначим

kh² . mgl

J ^, J

- B . С учетом введенных обозначений динамика системы будет описываться

следующими уравнениями:

^Z1 = z 2

z ² = A 1 z 1 + B 1 z 3 + и

Z 3 = z 4

. z 4 = B 2 z + A 2 Z з

s

или, в матричной форме,

Z = Q z + bu ,

где Q =

A 1

I B 2

B 1 0

⁰ J

b =

Г 01

. 0 >

Сформируем алгоритм управления по принципу обратной

связи: u = -D • - • arctan (z x c), где D - параметр, характеризующий «интенсивность» управ- п ления. Отметим, что при отсутствии управления (D = 0) поведение системы будет определяться собственными числами матрицы системы. Эта матрица имеет четыре собственных числа:

\2

A 1 + A 2 + У( A 1 — A 2 ) 2 + 4 B i B 2  .

О                        ’    3,4

^А1 ⁺ A 2 —У ( A 1 - A 2 ) ^{+ 4 B}1^B B 2

. Два из них

Z X вещественные (одно положительно, второе отрицательно), а два других - чисто мнимые. Очевидно, что фазовое пространство делится на два подпространства. Колебания в одном из них (которое соответствует комплексным собственным числам) будут соответствовать особой точке центр, а во втором подпространстве особая точка – седло [8].

Таким образом, задача стабилизации нулевого положения, соответствующего вертикальному положению обоих маятников, заключается в подавлении эффекта положительного собственного числа [14]. Такая система детально описана в работе [15], в которой было показано, что при достаточно большом значении параметра D система (2) стабилизируема, - т.е. фазовые координаты остаются в ограниченной области фазового пространства. В настоящей рабо- те рассматривается пружина с нелинейной жесткостью, а именно предполагается изменение жесткости по закону k = к0 (1 + x2),

где x = h ( ф ! - ф₂ ) или, во введенных выше обозначениях, x = h ( z 1 - z 3 ) . Таким образом, жесткость пружины, зависящая от взаимных отклонений маятников, является частью ди^намического управления. Перепишем систему (2), подставив в нее (5):

Ч = ^- 2

•

z 4 =

k 0 ( 1 ^{+ (} h ^{( z} 1 z 3 ) ) ) h

k ^{0 ( 1+( h ( - 1} z ³

»‘)

h ²

/

J ₂

z ₁

+

m ₂ gl ₂

J ₂

₊ k 0 ( 1 + ( h ( -

⁺             J 1

_

k 0 ( 1+ ( h ( - 1

—

z 3 ^{) )2} ) h ²

z 3 + и

. (6)

—

z ₃

))1

h ²

J 2

z ₃

V

mgl      k 0 h ²

Сделаем замену переменных —— = a , --- = p. Тогда система (6) примет вид

JJ

2/.

• ^{- 2}^-р^¹- ^{- 3}Ы * и- ^- I + u

• ^- 3 = ^- 4                                    3

• - ^- 4 a 2 z ₃+P^{2 ( - 1 -} ₃ ^{) +} Р 2 h ^{2 ( - 1 -} ₃ )

Как известно, динамика любой системы связана с ее поведением в окрестности стационарных решений [16]. В рассматриваемом случае стационарные точки определяются как решения следующей системы алгебраических уравнений:

- ₂ = 0'

« 1 - 1 -Р 1 ( - 1 - - 3 ) -Р 1 h ² ( - 1 - - 3 ) ³ + и = 0

z = 0 '

«^ ₊Р 2 ( _{- 1} - _{- 3} ) ₊ Р 2 h 2 ( _{- 1} - _{- 3} ) 3 = ₀

Тогда в фазовом пространстве существует три точки равновесия, из которых веществен- ные координаты имеет только одна:

z l

6r 2 h ²

-6Г 2 h ²Р₂ и

2<8 а 2 Р 2 h 2 Г 1 ^Г 2 Г з

_ I--------

+ ^12Г з

P i : ^

z, = 0

«1^2^132 h2 ( 2^!8гЗ - 6 и г2Гз -«2Р5)-^12«1Р2Г2

z ³                          6a₂p 1 h ²Г³₂Г₃

Z 4 = 0

где

Г , = а 1 а ₂ -а ₁ в ₂ -а ₂ Р 1 , Г₂ = а₂ Ь 1 + а , b 2 ,

Г3 = ^9а2р3h4иГ52 + ^3«6р6h6Г92 (4Г3 + 27а2h2и2Г2) .

Исследуем устойчивость этого единственного стационарного решения. Для этого применим первый метод Ляпунова [17] по линейному приближению. Линеаризуем исходную систему в окрестности стационарного решения и найдем собственные числа матрицы линеаризованной системы:

det (0-Х E ) = 0,

дF где 0 =---, z = дz будет иметь вид

( z 1 ,z 2 ,z 3 , z 4 ) . В рассматриваемом случае матрица линеаризованной системы

0 =

0  10

^а -р ц + с х

c 2 Х

c»

где ц = 1 + 3 h ^{2 (} z

Р ₂ м       0 ^а 2 ^-р ₂ м

— z 3 Л Х = , "² d    _Х , z , и z 3

"(1 + ( z X c )2)

С 4 Х

определяются соотношением P 1 . Характери-

стическое уравнение (8) можно переписать в следующем виде:

X⁴ +ч 2 X²₊ Y , ^{X +} Y 4 = 0.

Подставим вычисленные ранее координаты точки P j и найдем собственные значения Х 1,2,з,4 . Во избежание громоздких выкладок дальнейшие вычисления приведем для случая, в котором: величина управления D = 10; начальная жесткость пружины к ₀ = 14.5; высота крепления пружины h = 0.1; длины ^{и массы} осцилляторов l ! = 0.1, l 2 = 0.15, m ! = 0.1, m 2 = 0.2. Получим ^{собствен}ные значения в точке P : λ = –1.0127 + i 0.7334, λ = –1.0127 – i 0.7334, λ = –0.6582, λ = –0.2453. Поскольку все показатели Λ < 0, то при данных параметрах система асимптотически устойчива [16].

Динамика системы при значениях параметров, описанных выше, и начальных условиях: z 1 [0] = -0.001, z ₂[0] = -0.001, z з [0] = 0.002, z ₄[0] = -0.002, изображена на рис. 2, 3.

Как видим, стационарное решение, определяемое координатами точки P , устойчиво по Ляпунову. Исследуем зависимость устойчивости стационарного решения от параметров к ₀ и D . Для этого зададим диапазоны изменения интенсивности управления D е ^[1;5^0] и параметра жесткости пружины к ₀ е [1;20], а значения остальных параметров зафиксируем. Как известно из [16], стационарное решение устойчиво, если старший показатель Ляпунова отрицателен. Т.е. область устойчивости в пространстве параметров к 0 , D определяется как решение неравенства Л = Л тах ( к 0 , D ) < 0. Результаты представлены на рис. 4.

На графике рис. 4 отмечены области устойчивости системы в пространстве параметров. В областях, помеченных синим цветом, показатель Ляпунова Λ > 0 – это значит, что система неустойчива. В белых же областях, наоборот, система асимптотически устойчива.

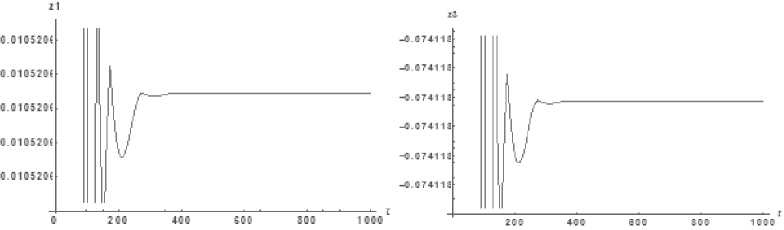
Рис. 2. Графики координат: z ₁ (слева) и z ₃ (справа)

Fig. 2. Velocity curves: z ₁ (left) and z ₃ (right)

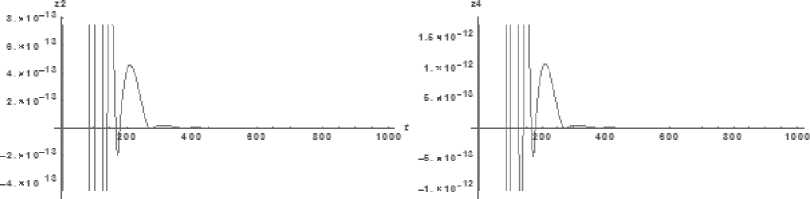
Рис. 3. Графики скоростей: z 2 (слева) и z 4 (справа)

Fig. 3. Speed graphs: z 2 (left) and z 4 (right)

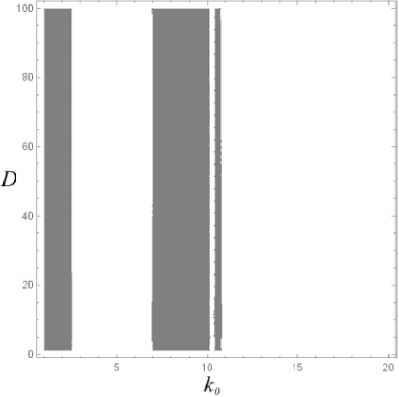
Рис. 4. Распределение значений Re[max(λ)] в зависимости от значений k ₀ и D

Fig. 4. Values distribution of Re[max(λ)] in terms of values of k ₀ and D

Случай управления обоими маятниками

Рассмотрим систему с нелинейной жесткостью и управлением, приложенным к обоим маятникам. Ее физическая модель представлена на рис. 5.

В данном случае в четвертом уравнении системы (4) добавится переменная управления и . Как и в предыдущем случае, имеется только одна стационарная точка:

1   ( бШа2Р1 h 2г1г2

+Vi2r3

18Г2h2^      Г z 2 = 0

а₁а₂р₁р₂ h ² ( 3^18Г 3 - 6 и Г 2 Г₃ ) -3^/18а , Г₃ z ³ =                18а₂ h 2 Г³₂Г₃

z 4 = 0

Матрица линеаризованной системы имеет вид

0 =

0	1		0
а 1 — Р 1 Ц + С 1 Х	С 2 %	Р ц + с 3 Х	С 4 Х
0	0	0	1
Р 2 ц + С 1 Х	С 2 Х	а 2 — Р 2 Ц + с з Х	С 4 Х

,

—2 d

где Ц = 1 + 3h (z — z3 ) , х =

, z и z определяются соотношением

„ ( 1 + („ с ? )

P 1 . Характери-

стическое уравнение эквивалентно полученному ранее

(X4 +Y1X3 + Y 2X2 +Y3X + Y4 0).

Найдем собственные значения Ху^. Во избежание громоздких выкладок, дальнейшие вычисления приведем для случая, в котором начальная жесткость пружины к ₀ = 100, остальные параметры такие же, как и в предыдущем случае. Получим собственные значения: Х 1 = -0.8794 + i 10.9709, Х₂ = -0.8794 - i 10.9709, Х₃ = -0.5705, Х₄ = -0.3231. Тогда показатели

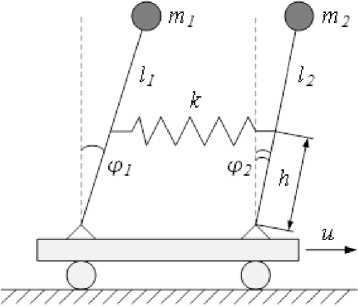
Рис. 5. Физическая модель связанных маятников

Fig. 5. Coupled pendulums physical model

Ляпунова: Λ1 = Λ2 = Reλ2 = –0.8794, Λ3 = λ3 = –0.5705, Λ4 = λ4 = –0.3231. Поскольку все показатели Λ < 0, то при данных выбранных параметрах система устойчива [16]. Результаты моделирования описанной системы представлены на рис. 6, 7.

Как видно из графиков (рис. 6-7), при моделировании с заданными начальными условиями система диссипативна. Исследуем зависимость устойчивости стационарного решения от параметров k 0 и D . Для этого зададим диапазоны изменения интенсивности управления D ∈ [1;50] и параметра жесткости пружины k ₀ ∈ [1;20], а значения остальных параметров зафиксируем. Результаты даны на рис. 8.

На графике рис. 8 отмечены области устойчивости системы в пространстве параметров. В областях, помеченных синим цветом, показатель Ляпунова Λ > 0 – это значит, что система неустойчива. В белых же областях, наоборот, система устойчива.

Заключение

В результате проведенного исследования было показано, что сложная неустойчивая система, состоящая из осцилляторов с нелинейной связью, может быть описана достаточно простой системой уравнений, а ее стабилизация при соблюдении определенных условий возможна с помощью достаточно простого управления периодической функцией по обратной связи.

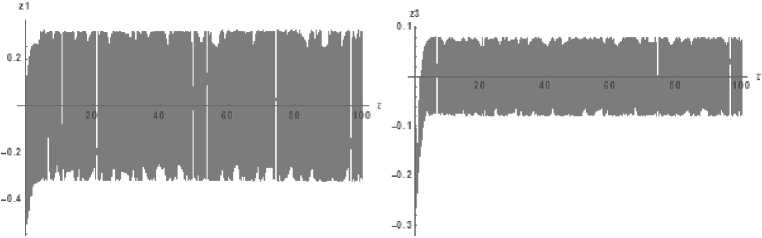
Рис. 6. Графики координат: z ₁ (слева) и z ₃ (справа)

Fig. 6. Coordinate graphs: z ₁ (left) and z ₃ (right)

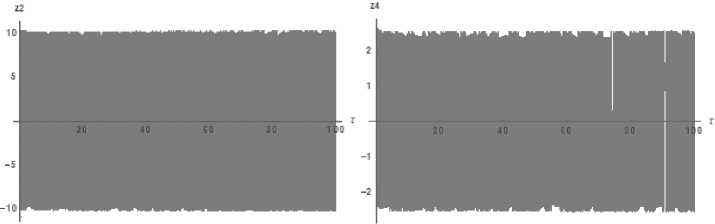
Рис. 7. Графики скоростей: z ₂ (слева) и z ₄ (справа)

Fig. 7. Velocity curves: z ₂ (left) and z ₄ (right)

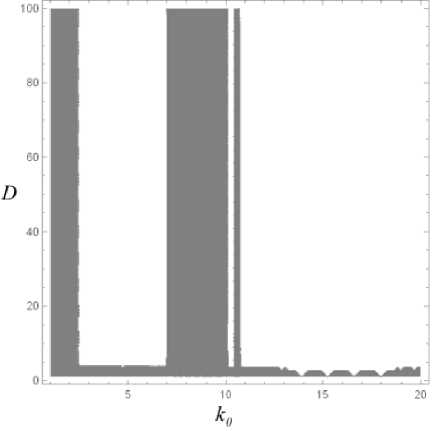
Рис. 8. Распределение значений Re[max(λ)] в зависимости от значений k ₀ и D

Fig. 8. Values distribution of Re[max(λ)] in terms of values of k ₀ and D

Работа выполнена при поддержке РФФИ, гранты № 17-01-00251, 16-08-00312.