Управление скоростью вращения частицы, захваченной сфокусированным лазерным пучком, с помощью жидкокристаллического модулятора

Оптический момент вращения эллиптически поляризованного света впервые был подсчитан Садовским в 1900 году [1]. Он считался слишком малым для экспериментального обнаружения, пока Бет в 1936 году в своём знаменитом сложном эксперименте не измерил его [2]. Он наблюдал отклонение кварцевой волновой пластинки, подвешенной на тонком кварцевом волокне, при прохождении через неё циркулярно-поляризованного света. В настоящее время при помощи такого инструмента как оптическая ловушка можно наблюдать передачу оптического момента вращения на микроскопическом уровне. Оптический момент вращения, рассчитанный в работах [3-5], указывает на то, что передача его поглощающей частице приведёт к её вращению со скоростью в несколько Герц. Свет передаёт угловой момент от поляризованной гауссовой моды поглощающей микроскопической частице. Угловой момент, несомый светом, может характеризоваться «спиновым» угловым моментом, связанным с круговой поляризацией. Изменяя степень поляризации лазерного излучения, можно менять скорость вращения микроскопических частиц. Авторы статьи [6] теоретически и экспериментально показали возможность двумерного захвата и манипуляций над поглощающей частицей остро сфокусированным гауссовым лазерным пучком. Более того, они показали, что использование гауссовой моды даёт новые возможности для изучения передачи оптического вращательного момента, обусловленного эллиптической поляризацией света поглощающим частицам. В работах [7-9] использовалась мода Лагерра-Гаус-са для демонстрации передачи орбитального и спинового угловых моментов от лазерной моды к захваченной частице.

Целью данной работы является разработка метода управления скоростью вращения микроскопической частицы, захваченной в фокус лазера, с помощью оптоэлектронного модулятора без механических перемещений в реальном времени. В настоящее время доступными манипуляциями над микрочастицами являются перемещение и вращение. Перемещение частиц осуществляется как путём сканирования сфокусированного лазерного пучка по плоскости изображения [7], так и перемещением предметного столика [9]. В последнем случае частица удерживается сфокусированным пучком, а перемещается окружающая её среда. Вращение частиц возможно за счёт использования циркулярной поляризации лазерного пучка [6] или использования лазерных мод со спиральными волновыми фронтами [7-9]. Управление скоростью вращения в реальном времени во всех работах [6-9] осуществлялось путём изменения степени эллиптичности поляризации лазерного пучка с помощью вращения пластинки 1/4. В данной статье реализовано управление в реальном времени скоростью вращения ча- стицы, захваченной сфокусированным лазерным пучком, при помощи жидкокристаллического модулятора (ЖКМ), способного изменять степень эллиптичности поляризации лазерного излучения без механических перемещений.

Теория

Найдём момент импульса вращения, приходящийся на единицу энергии светового поля. Электрическое поле эллиптически поляризованного пучка имеет вид:

ех=Е(х,у,1)со80е1к1-1®‘ e^iE^^^si^e^4® e1=g(x,y,1)elk1-imt,(1)

где

c

Тогда из уравнения Максвелла div E =0 находим связь между продольным и поперечным компонентами электрического вектора:

Ex cos0 + iEv sin0 + igk + — = 0 ^ x y g = -e-ik Jeikl (EX cos0 + iEy sin 0)dl =

= —(Ex cos0 + iE' sin0) = 6, kx             yl

, (2)

^d f где f x =d x,

f - df

fy = dy. Из уравнения Максвелла где значком « » отмечены сопряжённые величины. Подставляя в это выражение (1) и (3) для объёмной плотности углового момента получим:

M 1 = Re[-x(e e х B ₁ - B x e e 1 ) -

• - y(e e у By -e e 1 B y )] =

• 1    ^e x ^(EE) x ^+e y ^(EE)y .

=--- - sin 20 +

8nc2k

₊ 1 ( ^xe(E E y ^-E E y ) - ye(EE x -EEy) '

8nck0         2i2i

V7

Здесь первый член, зависящий от 0 , -поляризационная составляющая углового момента.

Объёмная плотность энергии светового

e поля W определяется как W = — НН . Тогда для удельного на единицу энергии поля поляризационного момента получим esin20 гrrx(EE)X + У(ее)У , , „ dxdydl т _    8nc            2k0

L ° =            e ггг -                 (6)

8 - JJJ EEdxdydl

Интегралы в (6) сведутся к двумерным, если взять толщину слоя А 1 такой, что I(x,y,1) = I(x,y) при 1 е (1₀ ±А 1). Тогда

B = — rot E ik 0

находим соответствующие ком

поненты магнитного поля:

B x

B у

k

= - i — Esin 0

k о

k

= —Ecos 0

k о

B = — (E sin 0 + IE cos 0 ) k о

Усреднённая по времени угловая плотность момента определяется следующим выражением:

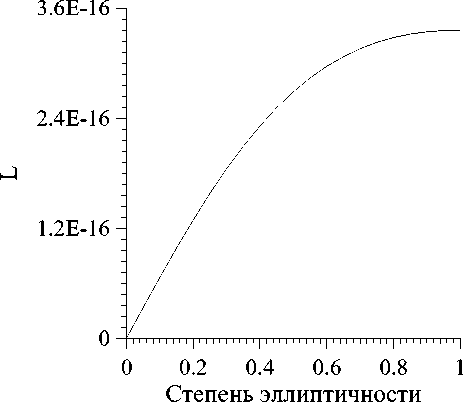
Рис. 1. Зависимость поляризационного момента L для различных степеней эллиптичности поляризации

M i = ^Re[ r x [ e E x B ]] i , 8 n c

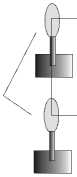
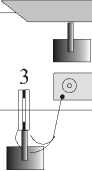
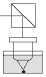
Рис. 2. Экспериментальная установка

1 - лазер He-Ne ЛГН-215; 2 - зеркала; 3 - ЖКМ;

• 4 - низкочастотный генератор; 5 - собирающая линза; 6 - светоделительный кубик;

7 - микрообъектив; 8 - кювета с частицами

L __ sin2 0 JJ^{( xI}X ⁺ YI y ) dxdy ° “    2 to       JJ Idxdy      ’

где to - угловая частота света.

С учётом того, что

JJ ( xI x + yI y ) dxdy _ — JJ 2Idxdy , окончательно получим:

L °

sin 2 0

to

Вид поляризационного момента (8) для различных степеней эллиптичности поляризации в = tg 0 и для to = 3 . 10¹⁵ с^-1 представлен на рис.1. Степень эллиптичности поляризации определялась нами как отношение составляющей вектора поляризации вдоль малой полуоси эллипса поляризации к составляющей вдоль большой.

Таким образом, вращательный момент M со стороны эллиптически-поляризованно-го света, действующий на частицу радиуса r и поглощающей способностью а , захваченную лазерным пучком радиуса w(z) и мощностью P, описывается формулой

M _

Ра 2в (.     J-2r2 1)

--1 _ expl—5 Г to 1 + в2 ^       [w2(z)

Эксперимент

Экспериментальная установка по вращению частиц в реальном времени представлена на рис.2. В нашем эксперименте мы использовали Hе-Nе лазер (ЛГН-215) (1) с максимальной выходной мощностью = 70 мВт. Для формирования оптической ловушки лазерный пучок при помощи светоделительного кубика (6) направлялся в поляризацион ный микроскоп МИН-8 с иммерсионным микрообъективом (7) (90x, NA = 1,25). Для совмещения плоскости изображения и фокальной плоскости микрообъектива перед микрообъективом располагалась собирающая линза (5) с фокусным расстоянием 0,1 м. Данная система позволяла формировать лазерный пучок с перетяжкой диаметром около 1,5 мкм. Максимальная мощность сфокусированного излучения, падающего на частицу, была 10 мВт. В качестве поглощающих частиц мы использовали частицы фторопласта-4 (диаметром 0,5 мкм), взвешенные в спирте. Эти частицы образуют при слипании более крупные частицы различных размеров и форм. Взвесь из таких частиц помещалась в кювету (8). Частота вращения фторопластовых частиц, захваченных в фокус гауссового лазерного пучка, измерялась для различных степеней эллиптичности поляризации падающего пучка после установления стационарного режима. Для изменения степени эллиптичности поляризации в реальном времени был собран ЖКМ (3), работающий на S-эффекте [10]. В нём использовался нематический жидкий кристалл 1348 с двойным лучепреломлением (Ан = 0,227 для X = 0,6328 мкм). Этот модулятор помещался на оптическую ось перед линзой (5) и управлялся низкочастотным генератором сигналов Г3-112/1 (4). Начальное направление директора слоя ЖК составляло 450 по отношению к поляризации падающего излучения.

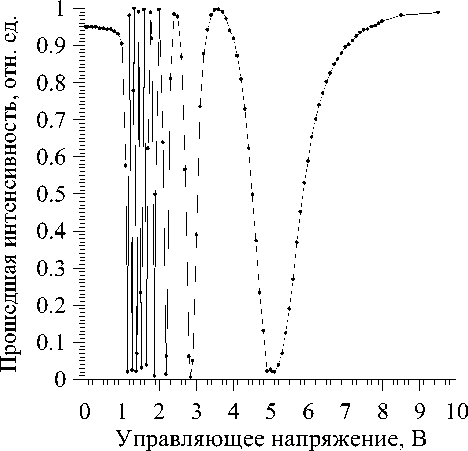
Рис. 3. Характеристика ЖКМ, снятая в скрещенных поляризаторах

4.1 4.2 4.3 4.4 4.5 4.6 4.7 4.8 4.9 5

Управляющее напряжение, В

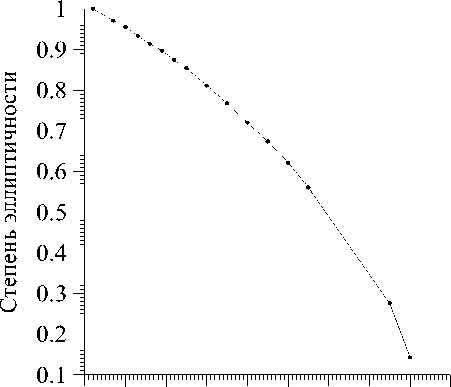
Рис. 4. Зависимость степени эллиптичности поляризации света, прошедшего через ЖКМ, от управляющего напряжения

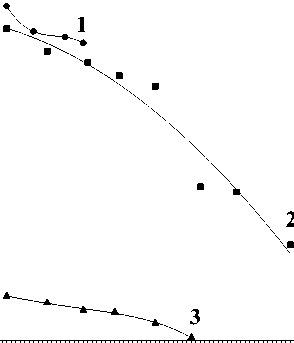
Степень эллиптичности

Рис. 6. Зависимость частоты вращения фторопластовой частицы от степени

эллиптичности поляризации лазерного излучения

На рис.3 представлена зависимость пропускания ЖКМ, находящегося между скрещенными поляризаторами, от приложенного управляющего напряжения частотой 10 кГц. Из этой зависимости видно, что наиболее удобно в экспериментах использовать участок зависимости от 4 В и выше из-за меньшей чувствительности к изменению управляющего напряжения. Из этой характеристики и подобной ей, но снятой при параллельной ориентации осей поляризаторов, было определено состояние поляризации

У tR К

и

в

о

0.12

0.11

0.1

0.09

0.08

0.07

0.06

0.05

0.04

0.03

0.02

0.01

• 4.1    4.2 4.3 4.4 4.5 4.6 4.7 4.8 4.9

Управляющее напряжение, В

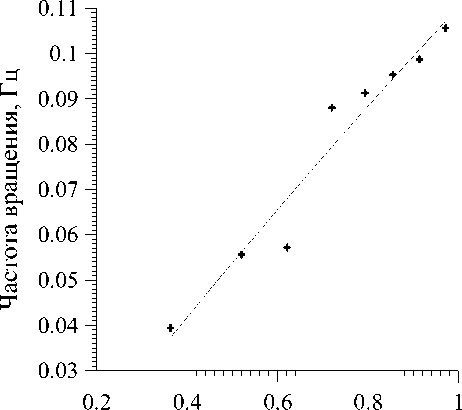
Рис. 5. Зависимость частоты вращения от управляющего напряжения для трёх разных частиц света после модулятора. Циркулярно-поляризованный свет получается при управляющем напряжении равном 4,12 В, а линейно поляризованный при 5 В. Управляющим напряжением на ЖКМ менялась поляризация прошедшего излучения от круговой до линейной и, соответственно, частота вращения захваченной частицы. Зависимость степени эллиптичности поляризации света, прошедшего ЖКМ, от управляющего напряжения для выбранного участка представлена на рис.4.

На рис.5 показана зависимость частоты вращения от управляющего напряжения на ЖКМ для трёх разных частиц, отличающихся по массе, форме и размеру. Чем легче частица, тем больше её частота вращения и, соответственно, выше график. Вращение наблюдалось до полной остановки частиц. Частица останавливались, когда вращательный момент становился недостаточным или к ней прилипала другая частица. Пользуясь данными, представленными на рис.4 и 5, можно получить экспериментальную зависимость частоты вращения фторопластовой частицы от степени эллиптичности поляризации лазерного излучения. Для частицы № 2 она показана на рис.6.

Работа выполнена при поддержке ФЦП «Интеграция» (проект 2.1 - 235) и РФФИ (грант № 99-02-16513).

ÑÏÈÑÎÊ ËÈÒÅÐÀÒÓÐÛ

• 1.    Sadowsky A. Acta Comment. Imp. // Universit. Jurievensis 7, 1, 1899; 8, 1. 1900.

• 2.    Beth R.A. Phys. Rev. 50,115. 1936.

• 3.    Marston P.L., Crichton J. H. // Phys. Rev A 30, 2508. 1984.

• 4.    Chang S.,Lee S.S. // J. Opt. Soc. Am. B 2, 1853. 1985.

• 5.    Barton J.P., Alexander D.R., Schaub S.A. // J. Appl. Phys. 66, 4592. 1989.

• 6.    Friese M.E.J., Nieminen T.A., Heckenberg N.R., Rubinsztein-Dunlop H.. Optical torque controlled by elliptical polarization // Optics

  Letters. 1998. Vol.23. ¹ 1.

• 7.    Simpson N.B., Dholakia K., Allen L., Padgett M.J. . Mechanical equivalence of spin and orbital angular momentum of light: an optical spanner // Optics Letters. 1997. Vol.22. ¹ 1.

• 8.    Friese M.E.J., J. Enger, H. Rubinsztein-Dunlop, N.R. Heckenberg. Optical angular-momentum transfer to trapped absorbing particles // Phys. Rev A. 1996. Vol.54. ¹ 2.

• 9.    Padgett M.J., L. Allen. Optical tweezers and spanners // Phys. World, 1997.

• 10.    Блинов Л.М. Эёектро и магаитооптика æèäêèõ êðèñòàëëîâ. Ì.: Íàóêà, 1978.

REAL TIME CONTROL OF THE ROTATION RATE OF A PARTICLE TRAPPED IN A FOCUSED LASER BEAM WITH THE HELP OF THE LIQUID CRYSTAL MODULATOR

Samara Branch of Physics Institute named for P.N. Lebedev of Russian Academy of Sciences

The real time control of the rotation rate of a microscopic particle trapped in a focused laser beam by change of the ellipticity of polarization of laser radiation has been studied. The change of the ellipticity of polarization was carried out with the help of the modulator using orientational S-effect in nematic liquid crystals. The dependence of the particle rotation speed on the state of polarization ellipticity was determined.

The calculation of an angular momentum of rotation per a unit of energy of the light field is shown.