Управление сложными экономическими системами методом нечетких классификаторов

Методика комплексной оценки эффективности хозяйственной деятельности занимает место в управленческом анализе [1]. Её применение позволяет получить:

• 1.    Объективную оценку прошлой деятельности, найти резервы повышения эффективности хозяйствования;

• 2.    Технико-экономическое обоснование перехода на новые формы собственности и хозяйствования;

• 3.    Сравнительную оценку товаропроизводителей в конкурентной борьбе и выбор партнеров.

В основе эффективности хозяйственной деятельности лежит интенсификация производства.

В настоящее время детально разработаны общие принципы методик оценки интенсификации производства. Стандартный алгоритм методики оценки включает в себя следующие этапы [2]: 1) определение качественных показателей использования ресурсов; 1) установление соотношение прироста ресурса в расчете на 1% прироста объема продукции; 3) расчет доли влияния интенсивности на прирост объема производства продукции; 4) определение относительной экономии ресурсов; 5) расчет комплексных оценок экстенсификации и интенсификации производства. Однако его реализация на практике зачастую затруднительна в силу препятствий как методологического, так и организационного характера.

Суть проблемы состоит в следующем [2], [3]. Практическое комплексной оценки основывается на анализе ряда показателей, отражающих экс-тенсификацию и интенсификацию производства. Показателями экстенсивности развития являются количественные показатели использования ресурсов: численность работающих, величина израсходованных предметов труда, величина амортизации, объем основных производственных фондов и авансированных оборотных средств. Показатели интенсивности развития — качественные показатели использования ресурсов, т. е. производительность труда (или трудоемкость), материалоот-дача (или материалоемкость), фондоотдача (или фондоемкость), количество оборотив оборотных средств (или коэффициент закрепления оборотных средств). Для формирования частных оценок для каждого из показателей, как правило, используются показатели темпов роста, представляющие собой отношение величины показателя в исследуемом периоде к его же величине в предыдущем периоде в процентах (Е=P2/P1). Полученные темпы подставляются затем в стандартные формулы, характеризующие степень преобладания интенсивного типа хозяйствования над экстенсивным. В случае, если данная комплексная оценка строится для небольшого (либо относительно однородного) предприятия за небольшое количество периодов существующие алгоритмы оценки позволяют получить удовлетворительный результат. Однако, если оцениваемое предприятие (либо даже отрасль производства) включает в себя множество подразделений (цехов, подотраслей и т.п.) сложность поставленной задачи возрастает на порядок и выходит за рамки стандартного экономического анализа. Возникает задача интегрирования полученных частных оценок по подразделениям и рассматриваемым периодам.

Вопросы исследования интегральных характеристик сложных объектов исследовались нами ра- нее на примере формирования их параметров при создании сложных структур ацентричных сегнетоэлектрических систем [4].

Математические методы в данной области еще недостаточно разработаны и выделяют две группы методов: детерминированной комплексной оценки и стохастической комплексной оценки [5], причем, стахостические методы широко применяются при высокоточных анализах параметров динамических систем [6].

Среди группы детерминированной комплексной оценки наиболее распространенным является метод сумм, при котором оценка рассчитывается простым суммированием фактических значений. Необходимым условием правильной оценки при использовании интегральных показателей, полученных по приведенной выше формуле, является однонаправленность исследуемых показателей, т.е. увеличение (уменьшение) значения любого частного показателя расценивается как улучшение результатов хозяйственной деятельности, а соответственно уменьшение (увеличение) значения частного показателя — как ухудшение результатов деятельности производственного объекта. Однонаправленность частных показателей позволяет ранжировать производственные объекты по возрастанию (убыванию) значений интегрального показателя.

Оценка результатов хозяйственной деятельности по методу сумм может строиться по различным частным показателям и не только в сравнении с планом, но и предыдущими периодами (оценка динамики) и с эталонными значениями показателей по группе производственных объектов.

Недостатком метода сумм является возможность высокой оценки результатов по интегральному показателю при значительном отставании по какому-либо частному показателю, которое покрывается за счет высоких достижений по другим частным показателям. В определенной степени этот недостаток может быть ликвидирован, если наряду с единым интегральным показателем рассчитывать два дополнительных показателя, отражающих отдельно сумму положительных и сумму отрицательных отклонений значений частных показателей от базы сравнения, однако существуют случаи, когда данный прием не гарантирует верный результат.

Метод геометрической средней предполагает расчет коэффициентов для оцениваемых показателей, заключенных на интервале от 0 до 1. За единицу принимается значение, соответствующее наиболее высокому уровню данного показателя. Этот метод целесообразно применять лишь в частном случае: при относительно малом числе оцениваемых показателей и в случае, если большинство их значений близко к единице. Следует отметить, что применение методов сумм, суммы мест, геометрической средней возможно только в случае однонаправленности влияния всех оцениваемых параметров на эффективность производства. В противном случае при расчете показателя комплексной оценки в качестве критериев берутся обратные к исходным величинам показатели.

Основой метода расстояний является учет близости объектов по сравниваемым показателям к объекту-эталону. Основной проблемой в этом случае является выбор эталона. За эталон может быть принят условный объект с максимальными элементами по всем показателям. В некоторых случаях типичным объектом считается такой, значения показателей которого равны средним арифметическим уровням показателей в изучаемой совокупности. Иногда предлагается использовать дополнительно в качестве эталона 100%-ное выполнение плана по всем показателям, указывая при этом на нежелательность как недовыполнения, так и перевыполнения плана. Однако в совокупности экономических объектов, где преобладают асимметрические распределения, среднее арифметическое в качестве характеристики типичного, эталонного объекта утрачивает свое значение.

Методы стохастической комплексной оценки включают в себя разнообразные экспертно-статистические методы, а также методы компонентного анализа, достаточно громоздкие и сложные в практическом применении.

В настоящей работе представлен метод построения комплексной оценки темпов роста интенсивности производства, а также ее динамики на основе анализа произвольной совокупности показателей за любое количество исследуемы периодов. Метод основан на применении систем нечетко-логического вывода, основанных на модификации 5-точечных классификаторов. применявшихся ранее в финансовом анализе для оценки риска банкротства фирмы [7], [8].

Предполагается, что необходимо рассчитать комплексную оценку интенсификации производства, а также ее динамики для некоторого подразделения (отрасли, цеха и т.д.) на основе статистических значений N экономических показателей за M периодов. Заданную статистическую информацию можно представить в виде таблицы 1.

Введем в рассмотрение лингвистические переменные:

• у - «комплексная оценка интенсификации производства»;

Р - «комплексная оценка темпов интенсификации производства».

Универсальным множеством для каждой лингвистической переменной является числовой отрезок [0,1], а множеством значений обеих переменных у, Р - терм-множество из пяти термов G = { G„ G ₂, G з , G ₄, G ₅} ,

• G₁ – «устойчивая тенденция к уменьшению роста»;

• G₂ – «тенденция к уменьшению роста»;

• G₃ – «тенденция к стагнации»;

• G₄ – «тенденция к росту»;

• G₅ – «устойчивая тенденция к росту».

Сразу же оговоримся, что количество термов «пять» выбрано из соображений лаконизма изложения и лингвистическую оценку интенсификации и ее темпов можно осуществлять, например, на основе множества из десяти термов.

Следующий этап задания лингвистической переменной состоит в задании функций принадлежности для каждого из термов. Функции принадлежности стандартного пятиуровнего нечеткого [0,1]-классификатора имеют упрощенную трапециевидную форму. Однако такое задание имеет ряд дефектов, таких как: 1) нарушение гладкости (и дифференцируемости) в вершинах, что может привести в дальнейшем при реализации численных алгоритмов решения; 2) конкретное и малообоснованное

Таблица 1

Числовые значения показателей

Обозначение показателя Значение показателя 1-й период 2-й период 3-й период М-й период Показатель № 1 X11 X21 X31 XM1 Показатель № 2 X12 X22 X32 XM2 Показатель № N X1N X2N X3N N XM задание интервалов кусочного задания функции; 3) специфический выбор узлов классификатора, приводящий к теоретической невозможности получения точного значения оценки «единица». Для увеличения математической строгости изложения введем в рассмотрение следующие функции при-

надлежности:

Мк = exp

2 n

-f, - k  11 / а=n

V

,

k = 1,2,3,4,5.                  (1)

Здесь n ∈ N , натуральное число, характеризующее крутизну графика функции принадлежности. Узлы классификатора, соответственно, располага-

ются в точках:

— k — 1

gk = T" k = 1,2,3,4,5

,

.

Графики функций принадлежности представлены на Рисунке 1.

Параметр о подбирается из расчета полноты построенной системы функций. Действительно, потребуем, чтобы в точках пересечения двух соседних графиков выполнялось соотношение:

< к -1 1)       < к -1 1)   1ц I+I = Ц I+I = k I 4      8 I ^k+iI 4      8 I 2

Тогда из формул (1) получим:

cr" =  —

82,1 In 2

Следовательно, окончательный вид функций принадлежности имеет вид:

A = exp

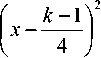
82"ln2

k = 1,2,3,4,5

Преимущество выбранных таким образом функций (3) состоит в том, значение каждой из них пренебрежимо мало (в контексте исследуемой задачи) в вершине соседней функции. Действительно, для уже n = 2

А (^а)=/^/ «1,53-IO"⁵

Было установлено [9], что на интервале между двумя вершинами с точностью до бесконечно ма-

лой величины выполняется равенство:

Цк (x )+ Mk+i (x ) = 1

k - 1 k ≤ x ≤

,

а в окрестности точки пересечения графики

аппроксимируются касательными к ним. Таким образом, система функций (3) удовлетворяет условию

полноты и может быть использована для построения пятиуровневого классификатора.

Очевидно, что формулы могут быть обобщены

на K-уровневый классификатор формулами:

Цк = exP

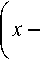
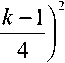
22"(^-l)2" In 2

— = k-1 gk = k _ 1

,

k = 1,2,..., K

На основании данных Таблицы 1 рассчитаем

вычислим числовые значения темпов роста исследуемых показателей (Таблица 2) и числовые значения скорости темпов роста (Таблица 2). Поскольку

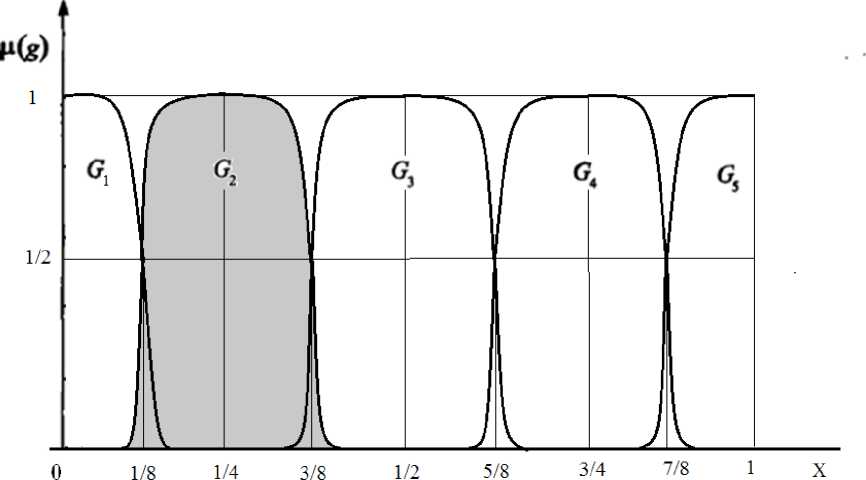
Рисунок 1. Система трапециевидных функций принадлежности на [0,1]-носителе

показатели из Таблицы 1, в силу экономического смысла, принимают только положительные значения, то величины из Таблиц 2, 3, теоретически, могут изменяться от нуля до бесконечности:

х^т^и^,^.

j

Полученные числовые значения T i , i - i , i = 2,3,..., M ,и S ii — 2 , i = 3,4,..., M , i = 1,2,..., N преобразуем к значениям нечетких числовых переменных путем применения одной из функций вида:

у^/(.х):[0,+Ю)^[0,1]

Например,

• V , = 1 -         , или          У 2 = expl — I,

• У1       x2 +1I

или          y3 = 0,5l 1 +—arctg(In x) I.(4)

I n)

Введем в рассмотрение лингвистические переменные:

• tⁱ – «темп роста i -го показателя», i = 2,3,...,M;

sⁱ – «скорость темпа роста i -го показателя», i = 3,4,...,M .

Множеством значений переменных ti, si явля- ются терм-множества из пяти термов

в1 = { b; , в 2, в 3, в;, в 5} , i  iiiii

C    {C 1 , C 2, C 3, C 4, C 5}

B 1 ⁱ , C 1 ⁱ – «очень низкий уровень показателя»; ii

B 2 , C 2 – «низкий уровень показателя»;

^B 3 ⁱ , ^C 3 ⁱ – «средний уровень показателя»;

ii

B 4 , C 4 – «высокий уровень показателя»;

^B 5 ⁱ , ^C 5 ⁱ – «очень высокий уровень показателя».

Значения соответствующих нечетких числовых переменных xⁱ , yⁱ , принадлежащих отрезку [0,1], получим, применив одну из функций (4) к числовым значениям Таблиц 2, 3. Результаты представим в виде Таблиц 4 ,5.

Функции принадлежности терм-множеств лингвистических переменных зададим формулой (3), как это сделано в предыдущем подпункте.

Таким образом, каждому значению показателей из Таблиц 4,5 будет сопоставлено значение функций принадлежности, относящих его к соответствующему терму лингвистической переменной. Таким образом, уже на данном этапе можно судить об уровне интенсивности производства по каждому показателю за конкретный интервал времени.

Таблица 2

Числовые значения темпов роста показателей

Обозначение показателя	Темп роста показателя на интервале
	1-й – 2-й периоды	2-й – 3-й периоды	…	(M-1)-й – M-й периоды
Показатель № 1	T 11 = X 2 / X 1	t22 = x 1 x 2		T 1      = Y 1 1 Y1 M, M - 1    M M 7 M M - 1
Показатель № 2	Th = X 2 / X 12	T2 — V2 / V2 T 3,2 X 3 / X 2		T 2     = Y 2 / r2 TM , M - 1    XM / X M - 1
Показатель № N	T 2 N 1 = X N / X 1 N	N  NN T 3,2 X 3 / X 2		N   NN T M , M - 1    X M / X M - 1

Таблица 3

Числовые значения скорости темпов роста показателей

Обозначение показателя	Скорость темпа роста показателя на интервале
	1-й – 3-й периоды	…	(M-2)-й – M-й периоды
Показатель № 1	V1 =T1 IT1 °3,1     1 3,2 7 1 2,1		Q1         rl      /T1 ° M,M - 2   1 M,M - 1 7 2 M - 1, M - 2
Показатель № 2	V2 = T 2 /Т2 ^ 3,1 T 3,2 / T 2,1		2           2      ,T2 SM , M - 2    T M , M - 1 7 T M - 1, M - 2
Показатель № N	N  NN ^ 3,1 T 3,2 / T 2,1		N  NN S M,M - 2 T M,M - 1 7 T M - 1, M - 2

Таблица 4

Значения нечетких числовых переменных темпов роста показателей

Обозначение показателя	Темп роста показателя на интервале
	1-й – 2-й периоды	2-й – 3-й периоды		(M-1)-й – M-й периоды
Показатель № 1, x 1	x 11	x 2		1 x M - 1
2 Показатель № 2, x	x 12	x 2 2		2 x M - 1
Показатель № N, xN	N x 1	N x 2		N x M - 1

Таблица 5

Значения нечетких числовых переменных скорости темпов роста показателей

Обозначение показателя	Скорость темпа роста показателя на интервале
	1-й – 3-й периоды		(M-2)-й – M-й периоды
1 Показатель № 1, y	y 11		y M - 2
2 Показатель № 2, y	2 y 1		2 y M - 2
N Показатель № N, y	N y 1 N		N y M - 2

Показатели уровня интенсификации производства, как правило, имеют различную значимость, поэтому требуется ввести весовые коэффи циенты для каждого показателя, kt , i = 1,..., N

N

(обязательное условие ^ k i = 1 ). Возможны следующие варианты:        ¹ = 1

– показатели равнозначны, следовательно, имеют одинаковые веса: k i = 1/ N ;

– показатели ранжированы в порядке убывания их значимости, веса определены по правилу Фишберна:

k = 2 (n - i + 1) .i     (n +1) n

– веса определяются на основе долевого вклада направления: например, если интенсификация определяется по трем группам, то вес каждой группы есть 1/3; если при этом внутри группы рассматриваются два направления, то вес каждого из них будет 1/3* ½ = 1/6, и т.д.

– веса определяются на основе оценок экспертов-экономистов (на основе парного сравнения альтернатив и т.д.)

Вначале рассмотрим простейший случай: формирование комплексной оценки интенсификации производства по данным Таблицы 1 за два последовательных периода. Соответствующие значения нечетких числовых переменных темпов роста показателей содержатся в первом столбце Таблицы 4.

В соответствии с правилами формирования оценок на основе 5-уровневого нечеткого классификатора, переход к весам термов лингвистической переменной Yi 2 = «комплексная оценка интенсификации производства (за к -тый - (к + 1) -й периоды)» имеет вид:

N

Pi =Z k A ⁽ x_k ) , l = 1,2,3,4,5 .   (5)

i = 1

(то есть вычисления проводятся для k -го столбца Таблицы 4: для них вычисляются функции принадлежности термов, записываются в виде матрицы 5 x 5, после чего ее столбцы скалярно умножаются на вектор весов показателей). Тогда значе ние самой оценки yk k+1 имеет вид:

Yk,к+1 = 2 pgi,            (6)

= 1

где g _l , узлы классификатора, определены формулой (2).

Заключительный этап - вычисление ц ( у _{кк + 1}) и ее лингвистическое распознавание в соответствии с заданным терм-множеством

G = G , G 2 , G 3 , G 4 , G ₅} .

Схема работы по описанному алгоритму представлена на Рисунке 2.

Как следует из определения термов, значение оценки y k k _{+ 1} <  0,5 указывает, в целом, на уменьшение интенсификации производства и необходимость анализа ситуации в целом. В случае,

Yk k+1 > 0,5 , но лингвистическое распознавание указывает на «тенденцию к стагнации», требуется провести анализ отдельных показателей и выбрать i из них те, для которых числовые оценки x минимальны. Очевидно, что именно эти показатели приводят к снижению значения комплексной оценки, и, следовательно, именно в данных направлениях должна вестись работа по улучшению ситуации.

Проведем расчет интегрированной оценки интенсификации производства для одного показателя за M исследуемых периодов. Формула для вычис-

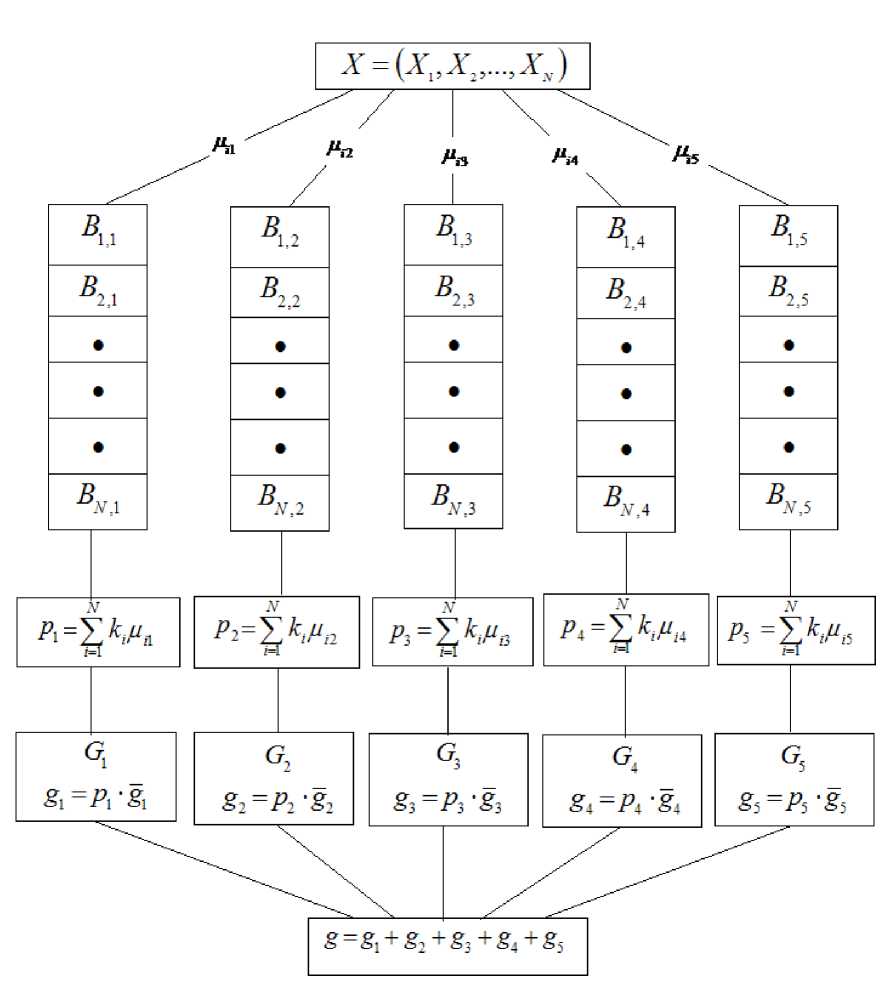
Рисунок 2. Общая схема вычисления комплексной числовой оценки g на основе числовых значений X = ( X _t, X_г ,..., X_N ) комплекса из N показателей;

здесь: k_t , i = 1,..., N , – веса показателей; g _l – узлы классификатора (фиксированы).

ления весов термов лингвистической переменной имеет вид:

м - 1

p = g Р^, (^;),        1 = 1,2,3,4,5, (5)

где р к - веса каждого из рассматриваемых пе-

M - 1

риодов, ^ p k = 1 ; в общем случае р k = 1/(M - 1); = 1

однако в ряде случаев «весомее» могут оказаться несколько последних периодов. Здесь вычисления проводятся для i -й строки Таблицы 4: для них вычисляются функции принадлежности термов, записываются в виде матрицы 5 x 5, после чего ее столбцы скалярно умножаются на вектор весов периодов).

Значение интегрированной оценки γ ⁱ вычисляется по формуле:

где g_l , узлы классификатора, определены формулой (2).

Как и в предыдущем случае, значение оценки Y ^ 0,5 указывает на уменьшение интенсификации производства в целом по i -му показателю (стабильный отрицательный прирост) и необходимость исправления ситуации в целом. В случае, y k k _{+ 1} >  0,5 , но лингвистическое распознавание указывает на «средний уровень показателя» (то есть отсутствие прироста), требуется провести анализ периодов и выбрать из них те, для которых числовые оценки x ⁱ минимальны. Именно в эти периоды имел отрицательный прирост, и необходимо попытаться выяснить, чем это было вызвано.

Таким образом, результатами расчетов по формулам данного пункта является комплекс интегрированных оценок по N показателям:

γ ¹ γ ²    γ ^N

,    ,…,    .

При расчете комплексной оценки интенсификации производства за M исследуемых периодов исходным материалом для вычислений являются результаты предыдущего пункта – рассчитанный комплекс интегрированных оценок по N показателям.

Переход к весам термов лингвистической переменной у - «комплексная оценка интенсификации производства»

осуществляется по следующей формуле:

p = 1 kiPi (Y ),           1 = 1,2,3,4,5. (7)

γ ¹ γ ²     γ ^N

(то есть для вектора (   ,    , … ,    ) вычис ляются функции принадлежности термов, записываются в виде матрицы 5 x 5, после чего ее столбцы скалярно умножаются на вектор весов показателей). Тогда значение самой оценки у имеет вид:

Y = Т Pg i

¹= 1            ,                       (8)

где g _l , узлы классификатора, определены формулой (2).

Заключительный этап - вычисление ^(Y ) и ее лингвистическое распознавание в соответствии с заданным терм-множеством

G = {G, G 2, G3, G4, G 5}

,

анализ полученных результатов по схеме, описанной в п.4.1 и 4.2.

Расчет/ 3 = «комплексной оценки темпов интенсификации производства» осуществляется по тому же алгоритму, однако в качестве исходных данных здесь выступают числовые значения из Таблицы 3.

Предложенный метод построения комплексной оценки интенсификации производства и ее темпов позволяет оценить состояние предприятия, отрасли и т.п. на основе совокупности рядов показателей интенсификации за произвольное число временных периодов.

Метод прост в применении, легко формализуем в виде программных комплексов.

Результатом применения метода является своеобразная «балансовая таблица оценок», в которую сведены унифицированные данные по показателям и периодам. Лингвистическое распознавание итоговой комплексной оценки позволяет судить о динамике процесса интенсификации в целом, а числовое значение соответствующей нечеткой переменной – дать ему количественную оценку («насколько плохо» или «насколько хорошо»).

Полученный результат легко анализируется на основе «балансовой таблицы оценок» и позволяет выделить показатели, понижающие итоговую оценку. В свою очередь, анализ оценок показателей с отрицательной динамикой помогает проследить развитие процесса и выделить периоды, в которых динамика была наихудшей. Полученная информация может служить основой для целевого детального анализа исследуемого производства и принятия соответствующих управленческих решений.