Управление температурным режимом нижних зон методических печей

Двусторонний нагрев металла в методических печах без теплоизоляции подовых труб или в случае ее неудовлетворительного состояния является существенно несимметричным [1]. Для методических печей стана 2500 ПАО «ММК», например, коэффициент несимметричности нагрева [2] может составлять 0,58…0,62, тепловой поток на металл в нижних зонах достигает лишь 62…72 % от потока в верхних нагревательных зонах печей [3]. Вместе с тем должная тепловая изоляция подовых труб и установка рейтеров позволяют в 10–20 раз уменьшить теплопотери с охлаждением труб, что приводит практически к вы- равниванию тепловых потоков на металл снизу и сверху, значительно улучшаются равномерность и качество его нагрева [4–6].

Несимметрию нагрева (несимметричность температурного поля сляба) иногда пы- таются компенсировать за счет повышения температуры рабочего пространства нижних нагревательных зон, при этом уставки (задания) локальных регуляторов температуры определяются по соотношению [7, 8]

⁽ нз     ^к( вз ,

где (нз, (вз - уставки локальных регуляторов температуры нижней и верхней зон печи соответственно; к - некоторый постоянный коэффициент. Понятно, что в данном случае к > 1,0; к сожалению, его численное значение выбирается, как правило, опытным путем, широко известной и обоснованной процедуры выбора коэффициента к не существует. Вместе с тем разработка такой теории позволит формализовать процесс определения числового значения коэффициента к, что повышает долю автоматически реализуемых функций автоматизированных систем управления технологическим процессом (АСУ ТП). Кроме того, если выяснится, что выбором численного значения коэффициента к можно удовлетворительно компенсировать несимметрию нагрева, то это создаст теоретическую основу допустимости рассмотрения процесса в симметричной форме, что во многих случаях приводит к существенному упрощению решения задач. В частности, при оптимизации управления печами [9] это позволяет в два раза уменьшить размерность искомого вектора управления, т. е. будет достаточно найти оптимальный набор температур рабочего пространства только верхних зон печей, задания регуляторам температуры нижних зон автоматически определятся по соотношению (1).

Модель несимметричного нагрева

Математическое описание динамики температурных полей верхней и нижней половин слябов в зоне нагрева представим следующим образом.

Общая часть описания в данном случае такова:

at(x,T)     а / at(x,-o\ „ .     . , , .

cP^^ = TxVA^^),00; (2)

t(x,0) = t0(x),0 < х < L;(3)

^^>0.(4)

Дополнительно для верхней и нижней половин сляба будем иметь соответственно:

Я ^ = Увз/[tвз(т), t(L, т)], т > 0;(5)

Я^ = Y нз f[кt вз (т), t(L,т)],т > 0. (6) Здесь с, р и Я - соответственно теплоемкость единицы массы, плотность и коэффициент теплопроводности, зависящие в общем случае от температуры t(x, т); х - пространственная координата; т - время; L - расчетное сечение, равное половине толщины сляба; t⁰(x) - заданная функция, описывающая начальное температурное поле металла; f - функция, описывающая внешний теплообмен металла: f = t_вз(т) — t(L, т) -при описании теплообмена в конвективной

Управление температурным режимом нижних зон методических печей форме, f=^<=V (Ю) * - _Пр_И описании теплообмена в лучистой форме; у_вз, У нз - параметры моделей внешнего теплообмена, причем при несимметричном нагреве, причем у_вз > у_нз [10]; t_вз - температура рабочего пространства в верхней нагревательной зоне печи.

В данном случае сляб мысленно разрезается по толщине на две равные части, при этом считается, что на линии разреза поддерживается нулевой градиент температуры и при переходе от одной половины сляба к другой изменяется на противоположное положительное направление отсчета пространственной координаты х. При этом нагрев верхней и нижней половин сляба представляется условно независимым. Нагрев верхней половины описывается уравнениями (2)–(5), а нижней половины соответственно уравнениями (2)–(4) и (6). Подчеркнем также, что использование условия (4) в математическом описании нагрева обусловлено самой постановкой задачи: обеспечить симметричное температурное поле в слябе. Суммарное охлаждающее действие элементов конструкции пода, согласно рекомендациям работ [10, 11], учтено меньшим значением коэффициента внешнего теплообмена, т. е. считается, что увз > унз; реальные численные значения коэффициентов увз, унз определяются при решении задачи параметрической идентификации модели нагрева металла [12–16].

Следует заметить, что модель собственно несимметричного нагрева сляба получается «склейкой» уравнений моделей для верхней и нижней половин с поглощением уравнения (4).

Постановка задачи

Анализ задачи показал, что невозможно обеспечить абсолютную идентичность профилей температурного поля верхней и нижней половин в процессе всего нагрева в зоне, следует ограничиться получением достаточно близких динамических траекторий для среднемассовой температуры. Поэтому на траекториях динамических систем (2)–(6) определим следующий функционал

.'<     _; - В ■ ■- Ут         (7)

где tВ(т) и tj[ (т) - среднемассовая температура верхней и нижней половин соответственно; Т - время нагрева в зоне печи.

Поставим следующую задачу оптимизации [17]: min_fc 1(к) - требуется определить такое численное значение коэффициента к, при котором критерий (7) принимает минимальное значение.

Решение задачи для линейного случая

Рассмотрим решение поставленной задачи при описании процесса полностью линеаризованным уравнением теплопроводности с конвективной формой внешнего теплообмена, при этом удается получить некоторые аналитические результаты. При этом будем считать, что t0(%) = 0, т. е. задача приводится к нулевым начальным условиям, что, как известно, не нарушает общности получаемых результатов [18].

Используя приведенное в [2] решение поставленной линейной задачи, нетрудно получить формулы для среднемассовой температуры верхней и нижней половин сляба. Подставляя эти формулы в критерий (7) и решая задачу его минимизации по к, найдем его оптимальное значение. Для случая, когда температура в зоне является постоянной величиной, оптимальное значение коэффициента к вычисляется по соотношению

к =

Jor[1-2”=1

2sin2^i exp (—^p?)

^i(^i + sin^icos^i)

■]-[1-2".1

2sin2niexp ^—^j^

ni(ni + sin^cos^i)

Jor{i-S“i[1-S“

2sin2niexp ^—^L?^

■ ]dx

,

- ¹ n i (n i + sinn i cosn i )

■ ] }2 dx

где ^ i и n i — корни уравнений ^Л/(у_взL) = ctgy и п^/(у_шL) = ctgn соответственно; а - коэффициент температуропроводности.

Как видно из формулы (8), оптимальное значение коэффициента к в практически значимом случае нагрева с постоянной температурой рабочего пространства в зоне не зависит от численного значения этой температуры, а определяется только теплофизическими свойствами стали, параметрами теплообмена, толщиной и временем нагрева сляба в зоне. Примечательно, как это следует из формулы (8), если у_вз = у_нз, то ^ i = n i для 1 = 1, « и будет к = 1, что и следовало ожидать, так как нагрев в этом случае реально является абсолютно симметричным. Отклонение численного значения коэффициента к от 1 определяется только тем, насколько у_вз отличается от у_нз.

Численный анализ полученного решения

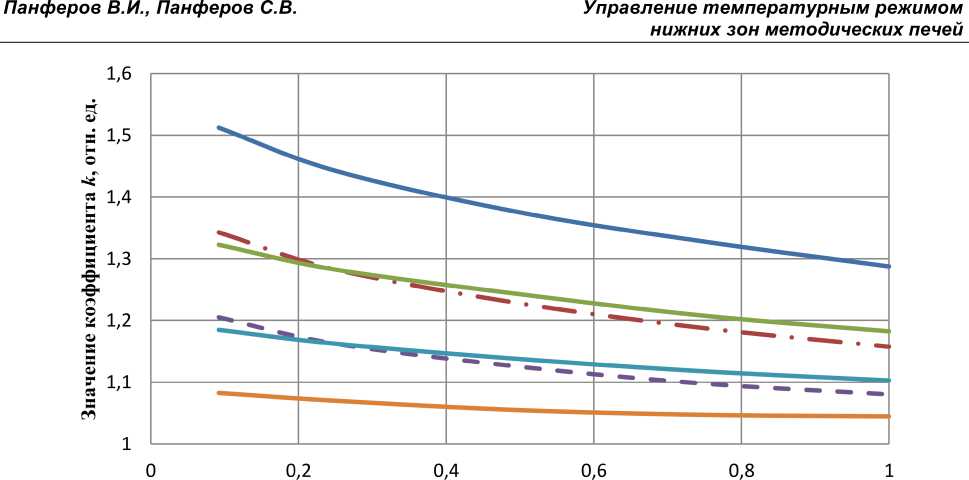
На рис. 1 для различных пар чисел Био, отвечающих нижней и верхней поверхностям сляба, приведено семейство кривых, изображающих зависимость оптимального значения коэффициента к от времени нагрева в зоне. При этом рассматривался нагрев углеродистых слябов с L = 0,1 м. Семейство сплошных кривых соответствует, считая сверху вниз, следующим значениям числа Био для нижней поверхности: 0,6; 0,7; 0,8; 0,9, число Био для верхней поверхности сляба во всех этих случаях равно 1,0. Кривая, отмеченная точками, соответствует числам Био 1,5 и 2, а кривая, изображенная штрих-пунктирной линией, числам Био 1,0 и 1,5 соответственно для нижней и верхней поверхностей сляба.

Как следует из рис. 1, оптимальное значение коэффициента к является монотонно убывающей функцией времени, следовательно, с увеличением времени нагрева в зоне для компенсации несимметрии требуется более низкий уровень температуры рабочего пространства в нижней нагревательной зоне печей, чем при меньшем времени нагрева. Другими словами, степень требуемого превышения температуры нижней зоны над температурой верхней зоны уменьшается.

При увеличении степени несимметрии (в данном случае степени различия коэффициентов внешнего теплообмена у_вз и у_нз) оптимальное численное значение коэффициента к возрастает, поэтому в этом случае при прочих равных условиях для компенсации несимметрии потребуется более высокий уровень температуры рабочего пространства в нижних нагревательных зонах печей.

Максимальный модуль относительной разности среднемассовых температур верхней и нижней половин сляба

Maximum modulus of the relative difference between the average mass temperatures of the upper and lower halves of the slab

№ п/п	Число Био для половины сляба, отн. ед.		Значение коэффициента к, отн. ед.	Максимальный модуль относительной разности среднемассовых температур, отн. ед.
	верхней	нижней
1	1,0	0,6	1,432 1,382 1,290	0,0084 0,0168 0,0403
2	1,0	0,7	1,277 1,245 1,185	0,0061 0,0122 0,0289
3	1,0	0,8	1,162 1,142 1,107	0,0039 0,0078 0,0184
4	1,0	0,9	1,071 1,063 1,047	0,0019 0,0038 0,0088
5	1,5	1,0	1,272 1,231 1,161	0,0104 0,0192 0,0394
6	2,0	1,5	1,156 1,128 1,084	0,0092 0,0161 0,0289

Время, ч

Рис. 1. Зависимость оптимального значения коэффициента k от времени нагрева для различных пар чисел Био для нижней и верхней поверхностей сляба Fig. 1. Dependence of the optimal value of the coefficient k on the heating time for different pairs of Biot numbers for the lower and upper surfaces of the slab

В работе провели численное исследование получаемой разности среднемассовых температур верхней и нижней половин сляба, при использовании оптимального значения коэффициента к для задания температуры ра-

бочего пространства нижней нагревательной зоны. В таблице приведены получаемые при этом максимальные модули относительной разности среднемассовых температур верхней и нижней половин сляба. Исходные дан-

ные для расчета соответствуют данным рис. 1. Причем в таблице значения коэффициента к и максимального модуля относительной разности среднемассовых температур верхней и нижней половин сляба приведены для следующих трех значений времени нагрева в зоне: 0,3; 0,5 и 1,0 ч, считая для каждой пары чисел Био сверху вниз соответственно.

Как следует из таблицы, при уменьшении времени нагрева в зоне во всех случаях максимальный модуль уменьшается, следовательно, в этом случае получаются более близкие динамические траектории для среднемассовых температур. Это достаточно понятно и вполне объяснимо, поскольку очевидно, что чем меньше длительность отрезка времени, тем точнее можно компенсировать несиммет-рию нагрева – точнее сблизить траектории нагрева верхней и нижней половин сляба. Также отметим, что из данных таблицы следует, что, как правило, за счет выбора численного значения коэффициента к удается получить практически удовлетворительное совпадение динамических траекторий для среднемассовых температур верхней и нижней половин сляба.

Нелинейный случай

В случаях учета зависимости теплофизических свойств стали от температуры и в описании теплообмена в лучистой форме для решения поставленной одномерной задачи оп- тимизации minkI(k) применяли метод золотого сечения. При этом уравнение теплопроводности аппроксимировалось неявной разностной схемой, для ее решения использовался метод прогонки [19, 20]. Интегралы вычислялись методом Симпсона. Зависимости теплофизических свойств стали от температуры брали из [21].

Исследование показало, что задача устойчиво и практически с любой наперед заданной точностью решается и в этом случае. Зависимость оптимального значения коэффициента к также является монотонно убывающей функцией времени, так же, как и в предыдущем случае, с увеличением степени несим-метрии оптимальное значение к возрастает. На рис. 2 для различных пар коэффициентов излучения приведены типичные кривые изменения оптимального значения коэффициента к в зависимости от времени нагрева в зоне. При этом коэффициент излучения для нижней поверхности сляба составлял 2,5; 2,6; 2,7; 2,8; 2,9 Вт/(м²·К⁴), считая по кривым сверху вниз, для верхней поверхности во всех случаях он равен 3,0 Вт/(м²·К⁴), рассматривался нагрев углеродистой стали с нулевой начальной температурой и t_вз = 1200 °С.

При использовании оптимального значения коэффициента к максимальный модуль разности среднемассовых температур верхней и нижней половин сляба не превосходил 10 град., что вполне приемлемо для практики.

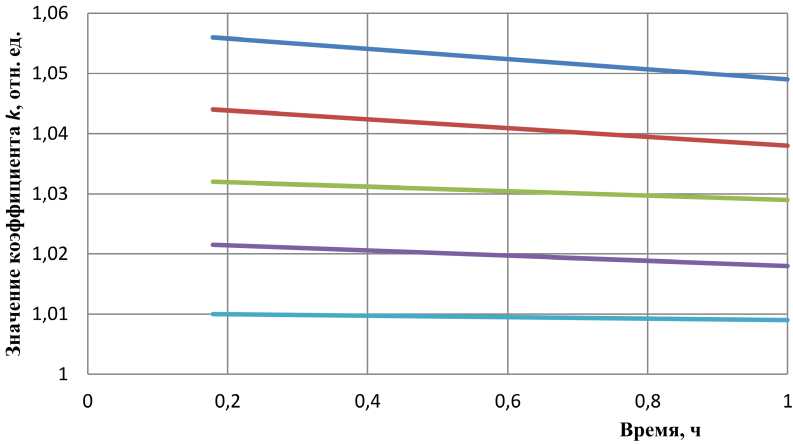
Рис. 2. Кривые изменения оптимального значения коэффициента k в зависимости от времени нагрева в зоне для различных пар коэффициентов излучения

Fig. 2. Curves of changes in the optimal value of the coefficient k depending on the time of heating in the zone for different pairs of emissivity

Упрощенный вариант алгоритма

При с, р, Л = const, следуя работе [22], проинтегрируем уравнение (2) по координате х в пределах от 0 до L и разделим обе его части на L, тогда получим dt = a rdt(L,r) dt(O,T)' dr L L dx dx .

где t(T) = ^- { ' t(x,T)dx - среднее значение температуры заготовки (среднемассовая температура).

Подставим теперь в (9) соотношение (4) и граничное условие для х = L, записанное предварительно в конвективной форме, тогда получим, что df=aL[tp„(r)-t(L,r)].

Здесь а - коэффициент теплоотдачи, при этом вполне понятно, что при вычислении среднемассовой температуры верхней половины сляба а = а_вз, а при определении среднемассовой температуры нижней половины сляба а = а_нз.

Если предположить, что температура поверхности t(L,t) равна среднемассовой температуре 1(т) = —/О' t(x, T)dx, как это имеет место для термически тонких тел, то уравнение (10) перепишется в виде dt

dr

= ^[Мт)- t], ^вр

где Т _вр = AL/(aa) - постоянная времени нагрева. Для верхней половины сляба Т _вр = Т _вз = = ЛL/(aа _вз ), а для нижней - Т_вр = Т_нз = ЛL/(aа_нз). Заметим, что предположение t(L, т) = t(T) является в значительной мере оправданным в рассматриваемом случае, так как L - это всего лишь половина толщины сляба.

Если динамику среднемассовой температуры верхней и нижней половин сляба описать упрощенной моделью (11), то для оптимального значения коэффициента к получается следующее соотношение к =

T - T вз

-

T нз

TT

I вз нз

T + T вз нз

^{| Т} вз ' =^ХР |^-_Г

V вз

^{+ Т} нз ■ ^еХР

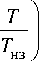
TT вз нз

T + T вз нз

■ exp

V

TT + T ))

У вз нз /

T T вз нз

T

T - 2 T + -нз + 2 T нз            нз

-

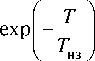
T (

-нз ■ exp - 2 ^|

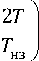
Здесь Т_вз = ЛL/(aa_вз) = ^L2/(_a^[ ), Т_нз = ЛL/(aа _нз ) = ^L2/(_a^[ ) - постоянные времени соответственно для верхней и нижней половин сляба. Как видно из формулы (9) при Т_вз = Т_нз ^ к = 1, что так и должно быть при такой конкретной постановке задачи. Кроме того, вполне очевидно, что данная формула заметно привлекательна как с точки зрения своей заметной «прозрачности» влияния исходных данных на вычисляемый результат - коэффициент к, так и с точки зрения объема требуемых вычислений.

Проведенное исследование показало, что различие числовых значений коэффициентов к, вычисленных по формулам (8) и (12), практически не существенно. Так, например, при числах Био 1,0 и 0,6 соответственно для верхней и нижней половин сляба, времени нагрева Т = 0,3 ч и прочих указанных выше равных условиях вычисленное по формуле (12) значение коэффициента к составляет 1,508. Отличие этого значения от его значения, приведенного в первой строке таблицы, составляет 2,58 %, что вполне приемлемо.

Выводы

Разработан алгоритм расчета оптимального соотношения уставок регуляторов температуры верхних и нижних нагревательных зон методических печей, обеспечивающий удовлетворительное совпадение траекторий среднемассовой температуры верхней и нижней половин сляба. Варианты алгоритма предусматривают возможность описания внешнего и внутреннего теплообмена как в линеаризованной, так и в исходной нелинейной формах. Предложен также и упрощенный вариант решения рассматриваемой задачи, когда динамика среднемассовых температур верхней и нижней половин сляба изначально описывается не уравнением теплопроводности, а обыкновенным дифференциальным уравнением первого порядка. Использование оптимального соотношения уставок позволяет, например, при решении задач оптимизации процесса в два раза уменьшить размерность искомого вектора управления, что весьма существенно. Результаты работы могут быть использованы в составе алгоритмического обеспечения АСУ ТП.