Управление тепловым режимом здания при комбинированной системе отопления

На практике зачастую приходится иметь дело с системами отопления, содержащими комбинацию нескольких различных приборов отопления, например, воздушного и радиаторного с жидкостным теплоносителем. Также встречаются приборы отопления, состоящие из радиатора, создающего радиационную составляющую, и воздушного вентилятора, при включении которого обеспечивается повышение конвективной составляющей прибора [1].

Из-за различных технических характеристик приборов воздушного и радиаторного отопления, эффективность их использования при заданном тепловом режиме зависит от различных параметров объекта управления, таких как? например инфильтрационные и трансмиссионные тепловые потери, от использования общеобменной вентиляции, а также от стоимости тепловой и электрической энергии [2]. Задача эффективного управления тепловым режимом здания усложняется при наличии дневного и ночного тарифов на электрическую и тепловую энергию, и заданного графика изменения температуры во времени.

В России комбинированное отопление наиболее часто применяется в выставочных залах, торговых центрах и других объектах с заданным графиком изменения температуры во времени.

В работе [3] была сформулирована задача оптимального управления тепловым режимом здания при комбинированной системе отопления в следующем виде.

Математическая модель объекта управления, которым является отапливаемое помещение, в переменных состояния имеет вид:

dTa,int dt      av1Ta ,int

ТВ       ТР

- ^a 1,2 T surf + ^a 1,5 Q   + ^a 1,6 Q conv + ^a1,11 T a , ven ;

dT surf

= ^a 2,1 T a ,int

^a 2,2 T surf + ^a 2,3 T w + ^a 2,7 Q rad ;

dTw dt " a3,2Tsurf

^a 3,3^Tw + ^a 3,4 T surf , ext ;

dT . , surf , ext dt

= ^a 4,3 T w   ^a 4,4 T surf , ex

+ ^a 4,10 T a , ex _t ;

Q          ТВВ dt - a 5,5 Q   + a 5,8u ;

ТР

Qrad          ТРР

---;-- = - ^a 6 7 ^Q rad + ^a 6 9 u ;

dt ,,

ТР conv            ТРР dt       a7,6Qconv + a7,9u ;

уравнение выхода

TSU (t) = z1Ta ,int + z2Tsurf + z5 Qconv + z6 Qrad , при ограничениях:

0 <  Q ^ТВ( t ) <  Q mBx ;

0 <  Q Td ( t ) + Q conv ( t ) <  Q mPx ;

0 < u P( t) < u mmax;

⁰ <  u ^{В (} t ) <  u m _a x ;

T SSU ,min ⁽ t ) <  T SU ⁽ t ) <  T SU ,max ⁽ t )•

При регулировании тепловой мощности воздушного отопления за счет изменения расхода воздуха через теплообменник (плавное управление вентилятором) и температуры жидкостного теплоносителя используется дополнительное ограничение вида

Q ⁽ t ) = ^a ₈ ,20 u •                                                                                  ⁽⁴⁾

При регулировании тепловой мощности воздушного отопления только за счет изменения температуры жидкостного теплоносителя, подающегося в теплообменник (релейное управление вентилятором), используется дополнительное ограничение вида:

x ЭВ = 1, при u ^B >  0;                                                                       (5)

x ЭВ = 0, при u ^B = 0.

В выражениях (1)–(5):

a i,j – постоянный коэффициент, соответствующий номеру строки i и столбца j матрицы коэффициентов правой части системы уравнений (1);

z j – постоянный коэффициент, с номером j , определяемый в процессе идентификации математической модели объекта управления;

переменные состояния:

T_{a ,int} – температура внутреннего воздуха;

T_surf – температура внутренней поверхности ограждения;

T_w – температура слоя внутри ограждения;

T_{surf , ext} – температура наружной поверхности ограждения;

T_SU – результирующая температура [4];

T_S^S_U – заданное значение результирующей температуры;

Q ^ТВ – конвективные теплопоступления от воздушного отопления;

Q_r ^Т _a ^Р _d – радиационные теплопоступления от радиаторного отопления;

Q_c ^Т _o ^Р _nv – конвективные теплопоступления от радиаторного отопления;

Q ^ЭВ – электрическая мощность, потребляемая вентилятором воздушного отопления;

x ЭВ - переменная состояния вентилятора воздушного отопления (при x ЭВ = 1 - вентилятор включен, при x ЭВ = 0 - отключен);

управляющие воздействия:

u ^Р – сигнал управления приборами радиаторного отопления;

u ^В – сигнал управления приборами воздушного отопления;

возмущающие воздействия:

T_{a , ext} – температура наружного воздуха;

T_{a , ven} – температура воздуха, поступающего в помещение от приточной вентиляции;

Q _m^ТВ_ax , Q _m^ТР_ax – верхняя граница тепловой мощности для приборов воздушного и радиаторного отопления соответственно;

umВax , umРax – верхняя граница сигнала управления для приборов воздушного и радиаторного отопления соответственно;

T_S^S_{U ,min}( t ), T_S^S_{U ,max}( t ) – нижняя и верхняя границы для результирующей температуры.

Критерий оптимальности управления имеет вид

Jc(U,X) = J ^c?E? + ^jE? + EТВ) о L *=1              j=i dt ^ min,

где ciЭ , cТj – стоимостные коэффициенты для соответствующего тарифа электрической и тепло- вой энергии соответственно; EiЭВ – количество электрической энергии, потребленное по i-му тарифу воздушным отоплением; EТj Р , EТj В – количество тепловой энергии, потребленное по j-му тарифу радиаторным и воздушным отоплением соответственно; l1, l2 – количество различных тарифов, действующих в течении цикла работы системы отопления по заданному графику (за 24 часа) для электрической и тепловой энергии соответственно.

Постановка задачи упреждающего управления

Решение задачи оптимального управления в виде (1)–(6) вызывает значительные трудности из-за большой размерности и наличия ограничений [5–9]. Кроме того, решением задачи (1)–(6) являются функции изменения управляющих воздействий на всем временном интервале (за 24 часа), что приводит к значительным ошибкам при возникновении неучтенных возмущающих воздействий. В связи с этим практическое применение алгоритмов оптимального управления, полученных в результате непосредственного решения приведенной задачи, весьма затруднительно и может оказаться неэффективным.

Для решения задач такого вида на практике используются алгоритмы упреждающего управления [10–16]. Целью упреждающего управления является поиск оптимальных управляющих воздействий на заданном скользящем горизонте прогнозирования. Пусть X ( t ) – вектор переменных состояния, а U ( t ) – вектор управляющих воздействий, входящих в систему уравнений (1). Задачу упреждающего управления можно записать в следующем виде.

Требуется найти векторы управляющих воздействий для настоящего и последующих моментов времени с заданным шагом ( d = t ^ _{+ 1} - t_k ) и для заданного количества шагов N :

U ( t k ), U ( t k + 1 ),..., U ( t k + N ),                                                                                     (7)

которые обеспечивают минимум для целевой функции:

C(U,X) = f ЛТX(tk+J) + £ Л\U(tk+J-1) ^ min,(8)

j=1

где Λ 1 , Λ 2 – матрицы коэффициентов; N – горизонт прогнозирования.

Пусть для управляющих воздействий и переменных состояния заданы ограничения вида:

/ о <  U i ( t k + J - 1 ) <  u m ^ax;

>< Xi (tk+j ) < хГ,

J = 1... N, где xi, ui – элементы векторов X и U соответственно.

Система уравнений в дискретном виде, описывающая объект управления:

' X ( t k _{+ 1}) = A ^T X ( t k ) + B ^T U ( t k );

‘ X ( t k ₊ j ) = A ^T X ( t k ₊ j - 1 ) + B ^T U ( t k ₊ j - 1 );

X( tk+N ) = A T X( tk+N-1) + B T U( tk+N-1), где A, B – матрицы коэффициентов.

Поиск минимума целевой функции (8) осуществляется для временного интервала, который задается скользящим горизонтом прогнозирования N . При поиске минимума учитываются ограничения, наложенные на переменные состояния и управляющие воздействия. Результатом решения являются векторы управляющих воздействий U ( t k ), U ( t k _{+ 1}),..., U ( t k _{+ N} | ). Прогнозируемые значения переменных состояния X ( t k _{+ 1}), X ( t k _{+ 2}),..., X ( t k _{+ N} ) определяются исходя из рассчитанных значений управляющих воздействий. Вектор начальных значений переменных состояния X ( t_k ) является известным и может включать в себя реальные значения переменных в текущий момент времени [10, 17].

Одним из наиболее эффективных методов поиска решения при упреждающем управлении является метод линейного программирования [10, 11, 13, 14, 17].

В общем виде задачу линейного программирования можно представить следующим образом.

F ( U , X ) = X ₀ + Л X + A T U ^ min;                                              (11)

'c ^t X <  C o ;

D ^T U <  D o ;

A ^т X + B ^T U = E ₀, (13) где Λ 1 , Λ 2 , C , D , A , B – матрицы коэффициентов; C 0 , D 0 , E 0 – матрицы свободных членов; X ₀ - свободный член.

x i j >  0, u i j >  0 - обязательные условия для использования метода линейного программирования.

При решении задачи линейного программирования осуществляется переход от одной вершины допустимой области к другой, причем к такой, при которой значение целевой функции меньше (при задаче на минимум) [18, 17]. Оптимальная точка будет находиться на границе области допустимых значений заданной ограничениями (12) и удовлетворять выражению (13).

Для использования метода линейного программирования при решении поставленной задачи, необходимо привести выражения (11)–(13) к каноническому виду. Для этого нужно преобразовать ограничения, заданные в виде неравенств (12), в равенства. Это достигается путем добавления дополнительной переменной по следующему правилу. Если переменная добавляется в ту часть неравенства, которая расположена с меньшей стороны знака неравенства, то переменная записывается со знаком плюс. В результате система (12) примет вид

'T X + X ' = C o ;

DTU + U' = D0, где X', U' – векторы дополнительных переменных.

Приведем задачу (8)–(10) к виду, в котором ее можно решить с помощью метода линейного программирования.

Выражение (8) является целевой функцией в задаче упреждающего управления и имеет линейный вид. Уравнения, описывающие объект управления в задаче упреждающего управления (10), имеют вид аналогичный уравнению (13) задачи линейного программирования. Условие положительности из неравенства (9) обеспечивается из условия о положительности переменных при использовании метода линейного программирования. Верхние ограничения неравенств (9) приведем к каноническому виду путем добавления к левой части неравенств дополнительных переменных X ' , U ' . В результате, задача упреждающего управления примет вид:

NN

C (U,X) = £ ЛТ X( tk+J) + £ Л^( tk+J-1) ^ min;(15)

j=1

'^{0 —} u i , j ⁽ t k + J - 1 ) ⁺ u’ J = u max ;

0 — xi, j (tk+J ) + xi, j = xmax,

J = 1... N .

' X ( t k + 1 ) = A ^T X ( t k ) + B ^T U ( t k );

‘ X ( t k ₊ j ) = A ^T X ( t k ₊ j - 1 ) + B ^T U ( t k ₊ j - 1 ); (17)

;

X ( t k + N ) = A ^T X ( t k + N - 1 ) + B ^T U ( t k + N - 1 ).

Запись задачи (15)–(17) схожа с задачей линейного программирования (11), (14), (13). Отличие заключается в размерности. Поскольку задача (15)–(17) является динамической, то соответствующие ограничения записываются для каждого временного шага в пределах горизонта прогнозирования. А в целевую функцию входят переменные не только для текущего момента времени, но и для прогнозируемых шагов.

Таким образом, физический смысл решения задачи упреждающего управления методом линейного программирования заключается в переборе вершин области допустимых ограничений до тех пор, пока целевая функция не примет минимальное значение. Найденной вершине будут соответствовать оптимальные значения управляющих воздействий U ( t k ), U ( t k _{+ 1}),..., U ( t k ₊ N - 1 ), в пределах заданного горизонта прогнозирования N и соответствующие им прогнозируемые переменные состояния X ( t k _{+ 1}), X ( t k _{+ 2}),..., X ( t k ₊ N ). При этом для управления используется только ближайшее значение управляющего воздействия U ( t_k ) . При переходе на следующий шаг задача упреждающего управления формулируется и решается заново, учитывая новые начальные значения переменных состояния, и новые ограничения для шага k + N [11, 17].

Величина шага d = t k _{+ 1} - t k и горизонт прогнозирования N выбираются, как правило, опытным путем исходя из следующих соображений. Чем меньше значение шага d , тем меньше ошибка дискретизации модели объекта управления. Однако, чем больше количество шагов, для которых осуществляется прогноз, или другими словами, чем больше значение горизонта прогнозирования N , тем выше объем вычислений для поиска оптимального решения. С другой стороны, чрезмерное уменьшение горизонта прогнозирования сокращает временной интервал, в пределах которого осуществляется поиск оптимума, и может привести к запоздалой реакции системы управления на новые ограничения для шага t k ₊ N . Из вышесказанного следует, что выбор значений шага d и горизонта N зависит от таких параметров объекта, как быстродействие наименее инерционного звена объекта управления и располагаемой тепловой мощности приборов отопления.

Для использования метода линейного программирования при решении задачи упреждающего управления тепловым режимом здания необходимо преобразовать дифференциальные уравнения системы (1) в разностные и привести ограничения в виде неравенств (3) к каноническому виду. После преобразований получим выражения в следующем виде.

Математическая модель в дискретном виде:

T a M ( k + n ) = в 1 - [ M M ( k + n - 1) - a‘ 2 T surf ( k + n - 1) -

• ^{- a} 1,5 ^Q ТВ ^{( k + n} - 1) - ^a 1,6 Q COmv ^{( k + n} - 1) ^{+ a}'1,18^Ta , ven ^{( k + n} - ^1)];

T surf ( k + n) = в 2 - [ - a 2, T M ( k + n — 1) + a 2,2 T surf ( k + n - 1) -

• - ^a23 T W ^{( k + n -} 1) ^{- a} 2,7 Qrad ^{( k + n - 1)];}

T w ( k + n ) = в з - [ - a 3,2 T surf ( k + n - 1) + o^T , ( k + n - 1) -

<" a 3,4 T surf , ext ( k + n - 1)];                                                                                 (18)

T surf , ext ( k + n ) = в 4 - [ - a^ ( k + n - 1) + a 4,4 T surf , ex ( k + n - 1) -

• - a 4,17 T a , ext ( k + n - 1)];

Q ТВ ( k + n ) = в 5 - [ a 5,5 Q ТВ ( k + n - 1) - a 5,20 u ^B( k + n - 1)];

^{q T p ( k + n} ) = ^вб ^{- [ a} 6,6 Q rad ^{( k + n -} 1) ^{- a} 6,19 ^u Р ^{( k + n -} 1)];

QCOnv (k + n) = в7 - [a7,7QOiv (k + n - 1) - a7,19uР (k + n - 1)], где k - номер шага; n = 1^N, N - горизонт прогнозирования; в1 = в2 = вi = в7 = 0 - свободные члены соответствующих уравнений системы; ai j - постоянные коэффициенты, полученные в результате численного решения исходной системы дифференциальных уравнений. Для определения коэффициентов a’ j можно воспользоваться итеративным методом приближенного вычисления Рунге –Кутты четвертого порядка, обеспечивающим достаточно высокую точность и не требующим сложных вычислений [19]; i, j – номер строки и столбца матрицы коэффициентов правой части системы уравнений.

Уравнение выхода в дискретном виде:

T su ( k + n ) = zT a ,int ( k + n ) + z 2 T surf ( k + n ) + z 5 Q^ nv ( k + n ) + z 6 Q ^ d ( k + n ).                   (19)

Ограничения в каноническом виде:

x 1 ( k + n ) = в₉ - a ₉ , ₅ Q ^ТВ( k + n );

x з⁽ k + n ) = ^e_n^{- [ a} 11,6 Q^ d ⁽ k + n ) + ^a 11,7 Q COnv ⁽ k + n )];

x 5 ( k + n ) = в 12 - [ a 12,1 T a _M ( k + n ) + a 12,2 T surf ( k + n ) + a ₁₂ , ₆ Q^ ( k + n ) +

/a 12,7 Q COPnv ( k + n )];

x 4 ( k + n ) = - в 1з + [ a 13,1 T a _M ( k + n ) + a 13,2 T surf ( k + n ) + a 13,6 Q ^ d ( k + n ) +

^{+ a} 13,7 Q Conv ^{( k + n )];}

x 6 ( k + n ) = в₁₄ - a ₁₄ , ₁₉ u ^p( k + n );

x ₇( k + n ) = в₁₅ - a _{15 20} u ^B( k + n ). ^,

При плавном управлении вентилятором:

Q ^ЭВ( k + 1) = a ₈ ,20 u ^B( k + 1).

При релейном управлении вентилятором: x ЭВ ⁽ k + n ) = P 16 ^{- [ - a} 16,20 u ^{B (} k + n ) ^{- x} 8 ] ^;

xЭВ e{0,1} , где в9 = ОВ; Ри = Qmpx; Р12 = tSukmm; P13 = tSukmm, n = 1-n;

^в14 = u rnax ^{; в}15 = u rnax ^; a 9,5 = ^a 11,6 = ^a 11,7 = ^a 14,19 = ^a 15,20 = ^1;

^a 12,1 = ^a 13,1 = ^z1 ^{; a} 12,2 = ^a 13,2 = z 2 ^{; a} 12,5 = ^a 13,5 = z 5 ^{; a} 12,6 = ^a 13,6 = z 6 •

Критерий оптимальности управления (6) может быть также записан в дискретном виде. При достаточно малой величине шага дискретизации можно принять, что величина потребляемой энергии является константой в пределах шага. Тогда, энергию E в пределах шага d можно выразить через мощность Q следующим образом: E = Q • d . Запишем критерий (6) в дискретном виде:

NN

J c ( U ( t_k ) ,X ( t_k )) = £ [£ n Q ^ЭВ( k + n ) d ] + E£ n ( Q T d ( k + n ) + n = 1                               n = 1

⁺ ocL ^{( k +} n ) ) d ^{+ Q ТВ ( k +} n ) d ^ min,

где d = t k _{+ 1} - t k - величина шага дискретизации; с Э _{+ n} , с Т _{+ n} - стоимостные коэффициенты для электрической и тепловой энергии на соответствующем шаге.

Поскольку величина d в выражении критерия оптимальности входит в каждое слагаемое и является константой, то ее значение не влияет на результат решения задачи. Перепишем выражение критерия оптимальности без учета d для случаев с плавным и релейным управлением венти- лятором воздушного отопления.

При плавном управлении вентилятором воздушного отопления:

N

C E ^{( k} ) = Y o ⁺ Е Y^Э + n^{Q ( k + n} ) ⁺ Y k + n ( Q ^Td ^{( k + n} ) ⁺ Qconv ^{( k +} n ) ^{+ Q ( k +} n ) ) ]^ ^min ,     ⁽²⁴⁾

n = 1

где y₀ = 0 - свободный член; у Э _{+ n} = c ^Э( k + n ); у Т _{+ n} = c ^T( k + n ).

При релейном управлении вентилятором воздушного отопления:

N Э Э          Т ТР           ТР ce (k) = Yo + E YЭ+ nxЭ(k + n)+ YТ+n (Qrld (k + n)+ QCOnv (k + n)+ n =1

+

^ min,

где Y_o = 0 - свободный член; y Э _{+ n} = c ^Э( k + n ) Q ^ЭВ; y Т _{+ n} = c ^T( k + n ).

Таким образом, (18)–(20), (21), (24) представляют собой задачу линейного программирования, которая решается с помощью широко известного симплекс-метода.

Выражения (18)–(20), (22), (25) представляют собой частично целочисленную задачу линейного программирования, которая может быть решена с помощью симплекс-метода и метода отсечения (Гомори).

Алгоритмы решения задач линейного программирования без условий частичной целочисленности подробно рассмотрены в [18], а для частично целочисленных задач – в [20].

Моделирование работы системы упреждающего управления

Моделирование работы системы упреждающего управления проводилось в среде моделирования Simulink v7.5 программы MatLab v7.10.0. В качестве исходной модели объекта использовалась система дифференциальных уравнений (1).

В таблице приведены основные характеристики объекта управления, используемые в качестве исходных данных для моделирования.

Температура наружного воздуха T a,ext в процессе моделирования меняется по синусоидальному закону с периодом 24 часа, начальным значением (в момент времени t =0 часов) +5 °С и пределами изменения от +5 до –15 °С.

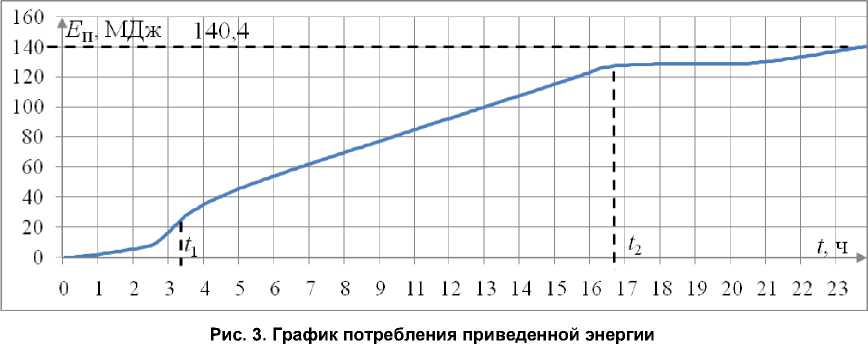
Для расчета приведенной энергии будем использовать следующую зависимость:

E n ( t ) = E ^ТВ ( t ) + 4( t^ E ^ЭВ ( t ) + E ^ТР ( t ).                                                    (26)

с ^Т( t k )

Исходные данные для моделирования

№	Наименование	Значение	Ед. изм.
1	Площадь ограждающих поверхностей	120	м 2
2	Объем помещения	300	м 3
3	Постоянная времени для радиатора отопления	0,85	ч
4	Постоянная времени для прибора воздушного отопления	0,2	ч
5	Тепловая мощность радиаторного отопления	4000	Вт
6	Тепловая мощность воздушного отопления	4000	Вт
7	Электрическая мощность вентилятора воздушного отопления	80	Вт
8	Величина шага дискретизации	800	с
9	Горизонт прогнозирования	5	шаг

Проведем моделирование работы системы управления при заданном графике изменения результирующей температуры и плавном управлении вентилятором воздушного отопления. Пусть стоимость электрической энергии превышает стоимость тепловой энергии в 2 раза в дежурном режиме и в 4 раза в рабочем режиме. Момент времени начала и окончания рабочего режима обозначим как t ₁ и t ₂ соответственно (рис. 1–3).

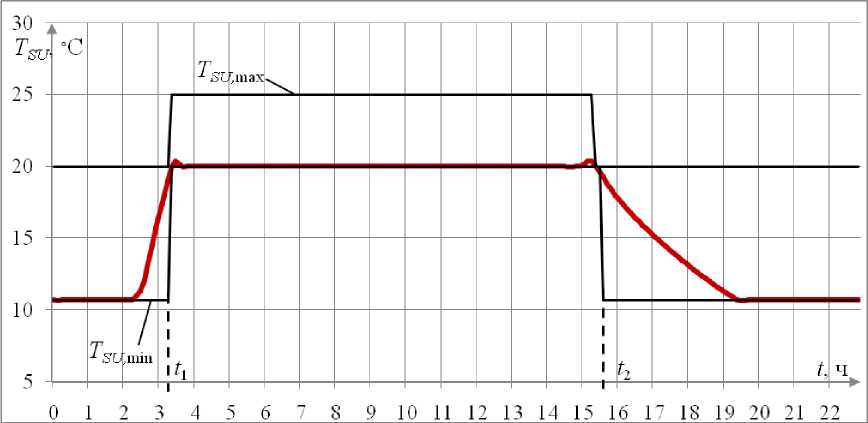
Рис. 1. График изменения результирующей температуры: T SU ,max , T SU ,min – верхнее и нижнее ограничение результирующей температуры соответственно

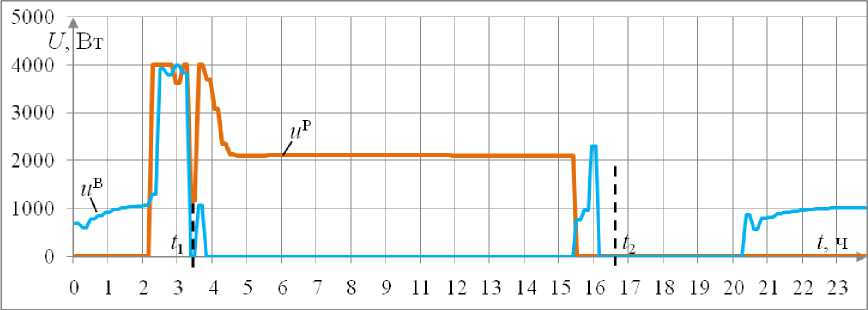
Рис. 2. График изменения управляющих воздействий: u ^Р, u ^В – управляющие воздействия для радиаторного и воздушного приборов отопления соответственно

Из рис. 2 видно, что в дежурном режиме для поддержания результирующей температуры используется воздушное отопление, поскольку радиаторное отопление требует большего количества приведенной энергии. Это связано с более высокой температурой внутренней поверхности стены помещения, чем при воздушном отоплении вследствие лучистой составляющей. Поскольку при радиаторном отоплении температура внутренних поверхностей ограждающих конструкций повышается, то в результате увеличения перепада температур между наружной и внутренней поверхностями стены возрастают и трансмиссионные теплопотери. Данный эффект наблюдается более выражено при сравнении воздушного и лучистого отопления [2]. При этом количество и стоимость электроэнергии, потребляемой вентилятором воздушного отопления, незначительны по отношению к стоимости и величине трансмиссионных теплопотерь при радиаторном отоплении. В процессе перехода из дежурного режима в рабочий используются одновременно радиаторное и воздушное отопление, что обеспечивает минимальное потребление приведенной энергии за счет интенсивного прогрева. В рабочем режиме стоимость электрической энергии относительно высока и поэтому в этом режиме используется радиаторное отопление.

Заключение

Задача упреждающего управления тепловым режимом здания при использовании комбинированного отопления была решена для двух типов систем воздушного отопления: при регулировании тепловой мощности за счет изменения расхода воздуха и температуры жидкостного теплоносителя воздушного отопления, и при регулировании тепловой мощности только за счет изменения температуры жидкостного теплоносителя, подаваемого в теплообменник системы воздушного отопления.

Приведены результаты моделирования работы системы управления. Полученные графики изменения результирующей температуры, управляющих воздействий и приведенной энергии поддаются аналитическому обоснованию, что показывает работоспособность разработанного алгоритма.