Управление токовой нагрузкой линий в кабельном канале с учетом сложного теплообмена

Уравнение неразрывности:

ϑ ∂ρ =ρ∂ϑi ∂x∂

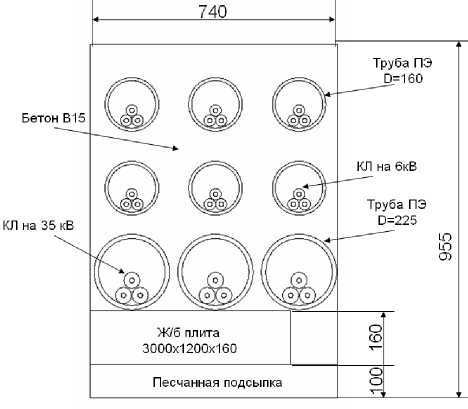
Рис. 1. Геометрические размеры кабельного канала

Уравнение движения:

∂ϑ   ∂p  ∂∂

ρϑ _j    ⁱ = -   + µ ⁱ + f_i

∂х     ∂x  ∂x∂

, f =Oy = ge(T-7°) у =0 xyz

^ρ

Уравнение энергии для воздуха:

dt dd

ρcϑi   = λ+ dxt   dXjd

,

Уравнение теплопроводности для:

- кабельных линий

5     dt d     dt

7— (Лк t-) +   (Л T-) + qv = 0

а х    a x    a y    a y ,

- массива земли

a      at     a      at

_?^(Лз —) +— ^(Лз —) - ⁰

а х ,      a x i     a y _t      a y ,

где ρ – плотность материала, xi – декартовые координаты, ^x, Sy -усредненные значения векто- ра скорости воздуха в канале, μ – вязкость среды; fi– сила конвективного переноса; с – теплоемкость среды, t – температура; λ – теплопроводность воздуха, qv – мощность внутренних источников тепла, λк – теплопроводность кабеля, λз –теплопроводность земли, t0 – температура 200С; β – температурный коэффициент плотности воздуха; g – ускорение свободного падения; v – кинематическая вязкость воздуха.

Система дифференциальных уравнений (1)-(5) замыкалась следующими граничными условиями:

• -    на твердых непроницаемых границах канала и на поверхности кабелей для компонент скоростей задается условие прилипания;

• -    на поверхности земли задано граничное условие третьего рода по температуре, коэффициент теплоотдачи α с поверхности земли равен 10 Вт/(м 2 ° С), а температура окружающей среды Т о - 20 ° С;

• -    на двух других границах в массиве земли заданы адиабатические условия теплообмена;

• -    на границах контакта разнородных сред задавались граничные условия четвертого рода и условия сопряжения температур.

  Жила

  

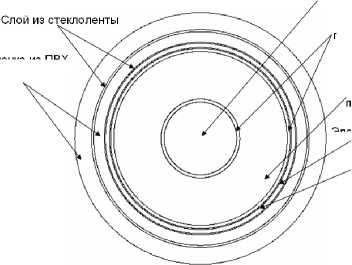
  Экран из меди

  Изоляция из полиэтилена

  Экран из полиэтилена

  Рис. 2. Конструкция кабеля АПвВнг-LS

  
  

Оболочка из ПВХ пластиката

Поставленная задача (1)-(5) решалась численно методом конечных элементов в среде инженерных расчетов Fluent. На первом этапе решения поставленной рассматривается процесс сложного теплообмена одной кабельной линии на 35 кВ с алюминиевой жилой и изоляцией из сшитого полиэтилена марки АПвВнг-LS с медным экраном сечением 35 мм2, конструкция которого представлена на рис. 2. Кабель расположен в бетонном коробе, проложенном в земле. Внутри канала воздух.

Решение задачи приводилось на различных сетках, число элементов которое изменялось в диапазоне от 50000 до 230000 узлов. По результатам расчета сходимость решения оценивается по значению выхода на прямую температуры на поверхности жилы. Сходимость решения задачи приведена на рис. 2 для кабеля со сложной конструкцией, где представлено изменение температуры на поверхности жилы кабеля. Очевидно, что для получения достоверных результатов (максимальная невязка по температуре не превышает 0,1%) для кабеля со сложной конструкцией можно ограничиться 190000 узлов. На рис. 4 представлено температурное поле в кабельном канале. Из рисунка видно, что максимальная температура жилы составляет 330С. Бо-

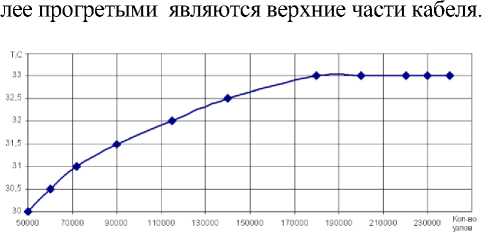
Рис. 3. Зависимость температуры на поверхности кабеля с многослойной конструкцией от количества разбиения на конечные узлы

Электропроводящий

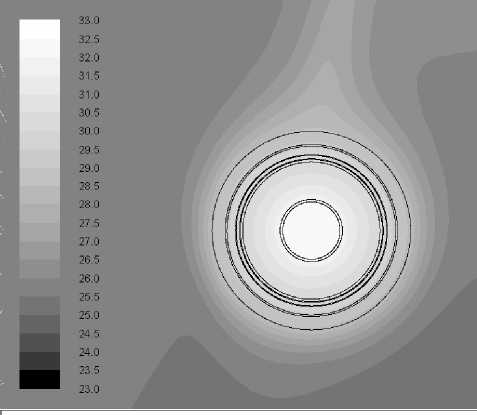
Рис. 4. Температурное поле внутри кабельного канала и кабеля со сложной конструкцией.

Для рационализации счета температурных полей 18 кабельных линий, расположенных в кабельном канале, многослойная конструкция кабеля заменена однородным полиэтиленовым монолитом с эквивалентной теплопроводностью. Эквивалентная теплопроводность рассчитывается как многослойный цилиндр по следующему выражению[4]:

λ экв

ln( d n ) ) d 1

i ln() у    di - 1

i       X i

где d i – диаметр i слоя кабеля, λ i – теплопроводность i слоя кабеля.

В табл. 1 приведены теплофизические свойства материалов. Сходимость решения задачи с упрощенной моделью приведена на рис. 5.

Таблица 1. Теплофизические свойства материалов

плотность воздуха, кг/м 3	1,000
теплоемкость воздуха, дж/кг.к	1,005
теплопроводность воздуха, вт/м.к	0,0242
теплопроводность бетона и грунта, вт/м.к	0,8
теплопроводность эквивалентного слоя, вт/м.к	0,258

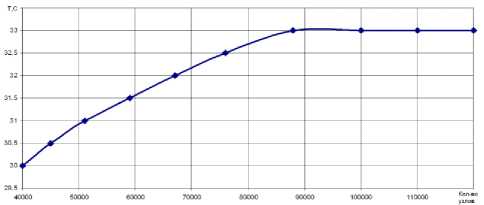
Рис. 5. Зависимость температуры на поверхности кабеля с эквивалентным слоем от разбиения на конечные узлы

Исходя из графика, температура на поверхности изоляции стабилизируется при количестве разбиения 90000 узлов, что в два раза меньше чем при рассмотрении сложной конструкции кабеля. Это является важным для решения задачи с 18 кабельными линиями. На рис. 6 представлено распределение температуры по поверхности кабеля с эквивалентным слоем.

Из рис. 4 и 6 видно, что температурное поле в кабельном канале и в том и в другом случае идентично. Температура на поверхности кабеля для обоих случаев составила 330С. Характер распределения температурного поля в кабеле со сложной конструкцией совпадает с распределением температуры в кабеле с эквивалентным слоем. Верхние части кабеля более прогреты, чем снизу. Это связано с движением воздуха в кабельном канале. В дальнейших расчетах используется кабель с эквивалентным слоем для оптимизации счета температурных полей.

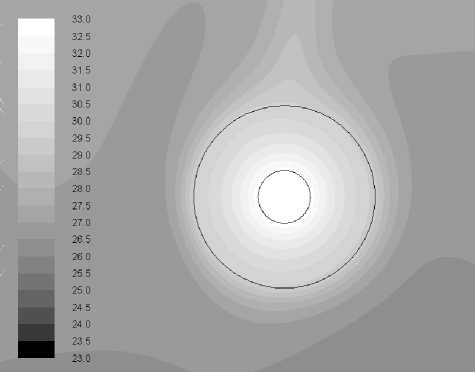
Рис. 6. Температурное поле внутри кабельного канала и кабеля с эквивалентным слоем

На втором этапе решена задача определения рациональной величины передаваемой мощности при различных режимах работы кабельных линий. Критерием ограничения по передаваемой мощности является значение максимальной температуры на жиле кабеля, которая не должна превышать допустимой температуры сшитого полиэтилена равного 900С. На рис. 7 представлено температурное поле в кабельном канале при максимально допустимой нагрузке кабельных линий.

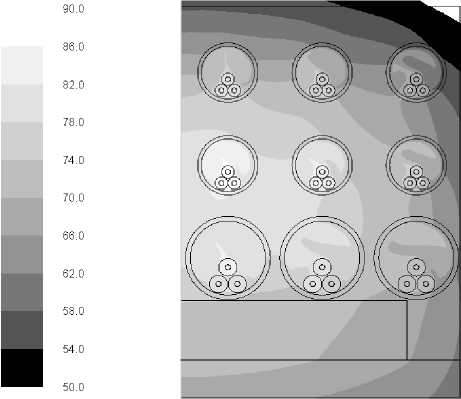
Рис. 7. Температурное поле внутри кабельного канала

По полученным температурным полям можно определить кабели, которые находятся в более жестких температурных условиях. Из рисунка видно, что кабели, расположенные ближе к центральной области канала, более нагреты, чем кабели, расположенные на периферии. Это необходимо учитывать при распределении нагрузки. В табл. 2 приведены результаты расчетов, полученные для различных режимов нагрузки кабельных линий.

Таблица 2. Эксплуатационные характеристики кабельных линий

Эксплуатационные характеристики	Количество нагруженных линий
	6	12	18
cуммарная мощность тепловыделения, Вт/м	27,9	35,04	37,8
рабочий ток, А	134	106,6	90,3
передаваемая мощность по одной линии, МВА	8,1	6,46	5,47
суммарная передаваемая мощность в канале, МВА	48,76	81,12	98,46

Исходя из результатов, представленных в таблице, появляется возможность оптимизировать передаваемую мощность в зависимости от реальных потребностей. В случае, когда надо передавать максимальную мощность по кабельным линиям на 35 кВ, то отключаем остальные кабельные линии и по кабельным линиям передается рабочий ток 134 А. С другой стороны, если нет особых условий для ограничения работающих линий, то суммарная передаваемая мощность составит 98,46 МВА, а рабочий ток составит 90,3 А.