Управление товарными запасами для многоассортиментных групп товаров

В логистике имеется разделение групп товаров по эффективности результатов реализации и по степени увеличения сырья (ABC и XYZ- алгоритмы [1]). Результаты применения методов ABC и XYZ позволяют ранжировать товары, поступающие на склад торгового предприятия по степени финансовой эффективности при их реализации или при увеличении спроса на тот или иной товар. В то же время классиче- к

ская модель управления товарными запасами (модель Уилсона [2]) разработана для планиро-

—    ¹⁼¹

^ k=iN_t

.

вания оптимального размера поставок для одно- номенклатурных запасов с идеальным и посто-

янным интервалом по времени их пополнения.

В данной работе производится модификация модели Уилсона с учетом разделения то-

Покажем, что оптимальный размер по ставки SonTi, определенный по формуле (2) обес-

варных запасов и использованием алгоритмов ABC и XYZ этого разделения. Основу модифи-

кации составляет предположение о том, что отношение затрат на завоз 1-ой партии товаров к затратам на хранение этой партии по всем товарным группам одинаково, хотя финансовая эффективность (выручка) от продаж этих групп то-

печивает минимальную сумму издержек на транспортировку и хранение i- ой партии для каждой группы товаров. Общие издержки на хранение С х и транспортировку С В выражается формулой (по каждой группе):

C i (S i ) — C_{B i} ^Qi + C x₁ ^S^-   (7)

S i            2

Найдем производную этой функ-

ции по S i и приравняем ее к нулю, то

варов различна.

На основании этого предположения

CX i T   C_B1Q t

-

можно модель оптимального числа поставок за интервал Т записат ь в виде:

Cx^iT

^j-^^i—1-k ' ⁽¹⁾

где   Cx1 - затраты на хранение одной партии

2        sf

Тогда:

— 0.

есть:

поставок;

Cb₁ - затраты на транспортировку одной

партии;

Q i - объем поставок для i -ой партии.

Обозначим величину:

! 2CB1

= Н = coast.

Cx 1 T

Тогда получим модель расчета оптимальных параметров товароснабжения для каждой товарной группы:

• 1.    Размер оптимальной поставки i-ой

• 2.    Средний запас текущего хранения для этой группы:

• 3.    Оптимальное число поставок:

группы товаров:

S0HTi = H^Qi;(2)

топт — ^_>;(3)

VQ

^О'  ^

Интервал между поставками:

T

• ti   — ^опт.(5)

Так как величина Н одинакова по всем

товарным группам, то ее можно также найти по формуле:

sr — j^ — HVoi-

То есть, получили формулу (2).

Вторая производная от функции C i (S i )

имеет вид:

2C5.Q;

CV(Si) — -^>0, si то есть функция (7) имеет минимум при SonTi — Si.

Из формул (7) и (9) получим минимальную сумму затрат для i-той партии в виде:

C r¹ — V2Q i C B_i C x_i T .       (10)

Если срок хранения каждой группы товаров одинаковый, то общая минимальная сумма издержек при поставке и хранении всех групп товаров:

C „i„ —E k _=iC i^ ⁱ ”            (11)

Если сроки хранения каждой группы товаров различны, то T=T i , то есть:

C^ — ^2Q i C B_t C xi Ti.      (12)

Расчеты по алгоритмам ABC и XYZ производим по стандартным методикам. Подробное изложение этих методик имеется в работах [1], [3]. По этим методикам находим матрицу при-

надлежностей товаров к той или иной группе

(элементу матрицы):

AX AY AZ

(ВХ BY BZ).            (13)

CX CY CZ

Каждую группу товаров из этой матрицы

рассматриваем как общую разновидность

В.И. Абрамова, М.С. Тихомирова, А.А. Юрова ассортимента с объемом Qi. При составлении каждой группы необходимо учитывать следующие соображения:

• 1.    Для товаров, входящих в группы AX, AY, AZ следует выработать индивидуальные технологии управления запасами. В частности, для товаров, входящих в группу AX, следует рассчитывать оптимальный размер поставки по формулам (1 – 10).

• 2.    Оптимальные параметры управления запасами в группе AY, BY, CY следует определять с учетом сезонности спроса. Для этого нужно рассчитывать оптимальные параметры отдельно по сезонным кварталам.

• 3.    В связи с большими колебаниями спроса для товаров, входящих в группу AZ, BZ, CZ необходимо определить существенный страховой запас по формуле:

Z = a_tt_b             (1⁴⁾

где    O; - среднее квадратичное спроса на i-ый товар определяется по формуле:

O ; = V ; X ; ,               (15)

где    V ; - коэффициент вариации i -го товара;

X; - средний спрос за период Т этого то- вара.

Заметим, что величина V; определена при XYZ - анализе на каждый из товаров этой группы.

Величина t i определяется как аргумент интегральной функции Лапласа (по таблицам нормального распределения) [4]:

F(ti) = 1 - 2а;, где с ■ х;

а ; =---- —;

^сдеф; ^{+ с}х;

с_х ; - расходы на хранение i -го товара;

с деф; - потери от дефицита при неудовлетворительном спросе на i -ый товар, вызванный случайным временем выполнения заказа т₃;

на этот товар.

^сдеф; = ^а;^Л;^(tз; ^{— Т}з; ^{— t};onm⁾ ,         ⁽¹⁷⁾

где     а ; - цена 1 ед. i-го товара.

Л ; = ^i .           (18)

tonm;

Величина α i рассчитывается для каждого из товаров группы AZ, BZ, CX.

Из этих величин выбирается наибольшее.

Величины 5_опт ; и t_onm ; определены по формулам (2) и (5) (см. рис.1).

S(t)

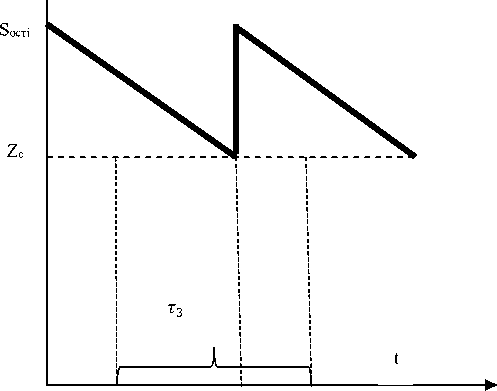
t 31                   t_t0 n      t 3 + Т з,

Рисунок 1. Зависимость оптимального размера поставки от времени