Управление величиной ошибки в нейронных сетях

одновременной настройки структуры весов и межнейронных связей. Одной из предпосылок, вызвавшей появление такого алгоритма, выступает сложность объективной оценки топологии сети[5, c.35-36]. Суть его заключается в следующем: кодируется как признак в генотипе ИНС число нейронов, а также величины связей, после чего вводятся операторы скрещивания, мутации и отбора. Популяции ИНС скрещиваются и отбираются с использованием усечения и элитарного отбора. Между тем, делается оговорка, что «не существует для некоторого алгоритма универсального оптимального набора параметров, позволяющего максимально эффективно решать любые поставленные задачи.»[5, c.103].

В этой же работе справедливо отмечается, что часто использование традиционных приемов обучения сетей не позволяет правильно определить компоненты выходной величины на примерах из обучающего множества, а также при необходимости работать с последовательностью выходов сети. Именно такой случай наблюдается при работе сети с адаптивной проводимостью сигнала для построения расписаний. Такая сеть не может использовать (для ряда сигналов) информацию о значениях ошибки ни в одном слое, кроме последнего. Это также повышает актуальность поиска иного научного инструментария для управления работой такой сети. Кроме того, вне зависимости от полученной конфигурации сети, задача ее эффективного функционирования сводится к задаче ее обучения, которое должно происходить наиболее эффективным образом.

К схожей задаче можно отнести попытку построения расписания с помощью уравнения Беллмана [10]. При этом применяется последовательное конструирование расписания с использованием принципа оптимальности любой части расписания, когда оно оптимально в целом. При формулировке задачи исходят из следующего:

Пусть T _i – длительность обслуживания i -й заявки,

Wi – время ожидания в очереди до начала обслуживания, ai - штраф за единицу времени ожидания результатов после поступления i-ой заявки,

Тогда длительность ожидания до получения результата:

V=T+W.

ii i

Штраф за ожидание можно записать следующим образом:

.

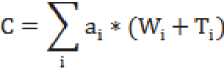
Обозначим через Di директивный срок решения каждой заявки. Если нам необходимо учитывать своевременное выполнение работы, то штраф будем определять по наибольшему или среднему нарушению директив сдачи i-й задачи. Критерий качества при этом определим как

С = max, а,{тах[О,(^ - DJ]}, где тах[О,(У8-П8)]– величина превышения директивного срока.

Несоблюдение директивного срока может наблюдаться не только для конкретных задач, но и для выполнения значительной части заявок. В этом случае используется критерий, учитывающий общий штраф за нарушение директивных сроков:

.

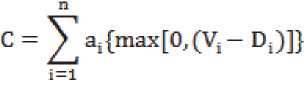
Тогда для суммы штрафов при оптимальной очередности обслуживания первых i заявок с вышеприведённой длительностью обслуживания i-й заявки Ti уравнение Беллмана будет иметь вид:

C_n(T) = mm_i[C_n_₁(T-T_i) + a_iT] . (1)

Это выражение имеет тот смысл, что при оптимальной последовательности решения всех n задач за общее время Т, последовательность решения n-1 задач за время Т-Ti также должна быть оптимальной. Тогда общий минимум штрафов достигается в той последовательности, когда перестановка обслуживания любых двух заявок не влечёт за собой уменьшение суммы штрафов.

Из (1) можно получить

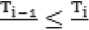
at-i at

Таким образом, оптимальное расписание следует составлять, руководствуясь правилом (2), т.е. в порядке неубывания отношения длительности штрафа к штрафу за единицу времени ожидания. В случае равенства штрафов за ожидание расписание составляется по неубыванию значений Ti. Также можно доказать, что при соблюдении такого правила будет минимальным среднее число заявок в системе и средняя длительность ожидания до начала реализации заявок[11].

Недостатком данного подхода является экспоненциальный рост числа возможных перестановок при увеличении числа заявок. Кроме того, рассмотренная задача слишком идеализирована и малоприменима для реальных задач, в особенности на железнодорожном транспорте, при составлении расписаний работы которого приходится учитывать как явные, так и неформальные ограничения. Это требует создания такого инструментария, который позволяет построить график полностью, которым и являются рассматриваемые ИНС.

Среди второй группы работ можно выделить наиболее значительные, в которых произведена попытка синтеза нейросетевого подхода и теории автоматического управления. В работе [3] идет речь о построении оптимальных временных последовательностей весов для динамической нейронной сети. В этой работе решается двухточечная краевая нелинейная задача управления, ведущая к правилам обучения сети. Оптимальная матрица функционирования сети выглядит как сумма (по всем индексам во всех выборках) внешних (векторных) произведений между вектором желаемых выходов размерности n и соответствующим выходом из определенной подсистемы, которые выделяются из системы N. Матрица весов на каждом шаге работы сети в итоге задается как оптимальная последовательность весов во времени. Авторы отмечают, что в идеальном случае весовая матрица в конечный момент времени соотносится с симметричной матрицей, эмпирически предложенной Дж. Хоп-филдом для ассоциативной памяти [1].

В векторном виде уравнение эволюции нейрона записывается как:

^ = -x(t) + ^(t)y(^(t)) , (3) где W(t) – блочно-диагональная матрица весов, каждый блок которой задается как матрица W1(t), g(x) – выход нейрона.

Начальные условия задаются как составленный из нескольких выборок вектор входа.

Минимизируемый функционал качества направлен на минимизацию величины, противоположной корреляции между выходом нейрона и желаемым выходным вектором в конечный момент времени управления. В процессе движения от момента начала управления до момента окончания управления функционал штрафует некоррелированность между желаемым выходом и функцией активации нейрона.

Оптимальное управление в данном случае отыскивается как задача Лагранжа для синтеза программного управления.

Авторы отмечают, что полученные результаты относятся к частному случаю нейронной сети, которая рассмотрена в [3].

Кроме того, существуют определенные сомнения в правильности оценки скорости изменения вектора фазовых переменных состояния нейронной сети как разности между желаемым выходом и расчетным выходом сети.

Предлагаемый подход также не позволяет работать с такими нейронными сетями, которые являются не полностью управляемыми, а управляемыми только по выходу. В то время как часть сетей характеризуется только параметрами, которые отражают выход, а не внутренние переменные сети.

Работа [4] посвящена разработке интеллектуального оптимального управления с динамическими нейронными сетями. Динамическая нейронная сеть описывается стандартными уравнениями эволюции нейрона, но на структурной схеме, описывающей состояния сети, присутствуют элементы, имеющие динамические звенья, такие, как: интегрирующее звено, усилительное звено, обратные связи (отрицательные), Такие системы при определенных параметрах матриц, описывающих поведение сети, могут приводить к возникновению предельных циклов, хаотических и существенно нелинейных движений. В качестве критериев качества обучения используются квадратичные функционалы, а также абсолютные отклонения. Авторы [4]также модифицируют алгоритм оптимизации BFGS.

Направление, рассматривающее нейронные сети как самоорганизующиеся системы, представлено в работе [4]. Согласно этому подходу, рост числа нейронов в сети задается как функция от активности сети, описываемой уравнением, однородным по своему классу с (3), а также распространением сигнала во внешней среде согласно уравнению теплопроводности. Условием роста структуры нейронов является достижение аксоном заданного нейрона некоторой точки, находящейся в зоне иного нейрона, причем величина зоны определяется пользователем. «Аксон при этом растет в направлении наибольшей концентрации вещества, участвующего в его создании»[6], а внешний сигнал, поступающий извне в сеть, определяет вектор изменения активностей нейронов.

Однако данная работа не сосредоточена на процессе функционирования нейронной сети.

Достаточно близко к теме исследования подошли авторы работы [7], которые ставили задачу управления нейронной сетью как системой с запаздыванием. При этом автором налагались ограничения на веса; математическая же модель нейронной сети работы [7] родственна модели, изложенной в [3]. Как и работа [3], такая модель не полностью соответствует рассматриваемой новой топологии нейронной сети с переменной проводимостью сигнала.

Таким образом, анализ работ, посвященных синтезу управления нейронных сетей, показывает, что данная сфера является изученной и проработанной в небольшой степени.

В частности, интерес представляет задача оценки состояния многослойной искусственной нейронной сети с переменной проводимостью сигнала[2], которая может быть использована для решения задач составления расписаний различных процессов, по наблюдаемому выходу сети или по значениям сигнала ошибки.

В этом случае мы сталкиваемся с проблемой способа формального задания эволюционных уравнений, причем возможны варианты задания их в матричном виде или в виде системы с одним входом и одним выходом.

В настоящей работе будет сделана попытка синтезировать оптимальное управление искусственной нейронной сетью с переменной проводимостью сигнала сначала как разомкнутой системой, а затем - как замкнутой.

При этом отметим, что в работе будет поставлена и решена задача Больца с квадратичным функционалом качества управления. Неприменимость линейных функционалов качества управления, а также задач на максимальное быстродействие к управлению нейронными сетями показана в [9] и в настоящей статье рассматриваться не будет.

Рассмотрим многослойную нейронную сеть с переменной проводимостью сигнала[2], состояние которой в каждый момент времени характеризуется дифференциальным уравнением: ~7 = Г=/ -/^v''.7 ~ 7.-::7 v'.7' ~ 7 - 7 ■ (4) где m – число гармоник, из которых состоит сигнал ошибки, в расчётах m = 7

ai , bi – косинус-коэффициенты и синус-коэф-фициенты, wi – частоты гармоник, определяемые спектральным анализом,

u(E, t) – некоторое искомое управление.

То есть, сигнал ошибки сети во времени может быть аппроксимирован в виде совокупности гармоник.

Предположим, что существует некоторое управление u , которое мы применяем к нашей нейронной сети в уравнении (4), чтобы перевести сеть из некоторого состояния в момент времени t₀ в целевое состояние в момент t₁.

Момент начала управления t0 определяется моментом пересечения траекторией Е(t) некоторой поверхности с заданным значением уровня ошибки ∆.

Момент окончания управления t1 является открытым и определяется в ходе решения задачи синтеза оптимального управления сетью. В содержательном смысле условие окончания управления записывается как Е(t)< ∆.

Синтез программного управления

Для сети, развивающейся в соответствии с (4) определим функционал качества как

. (5)

f0

Для задачи (5)-(6) запишем выражение гамильтониана:

H(E,t,u,4^f) = ^(t) * (Q}^₁(a_icos(w_jt) +

+ b_isin(w_it)')") + u(t)) ~ u²(t) — Е^) , (6) где ^(t) – вспомогательная функция.

Примем, что ограничений на управление не задано.

В соответствии с принципом максимума Л.С. Понтрягина найдем структуру оптимального управления:

^H^E, t,u, V) = V^t) - 2u(t) . (7)

Покажем, что действительно достигается максимум гамильтониана по управлению:

a²H(E,t,u,Y) -----U ^.

OU

Из равенства (8) нулю найдем структуру оптимального управления:

^UoptW - — ^.

Запишем систему канонических уравнений принципа максимума Л.С. Понтрягина с учетом гамильтониана (6):

Г - = - = u(t) + (^(OiCo^t) + ^яп(»^))) = ^ + Q^facostWit) + ^sihfw^))).

^(^)) “ ^07

ат эя л

— = — = at ан

Второе уравнение в (10) – начальные условия для уравнения (4).

Произведем проверку условий трансверсальности, чтобы получить недостающее для решения (10) условие. В общем виде условия трансверсальности с учетом (6) запишем как:

бЕ^") - Я(с_т) * 5t_T + ^(tj * 5E = 0 (11)

или

5ВД- V^t)* l^(aicos(ivjt) + bisin(wlt))Uu(t)

+Wi(ti) «6Е = 0

-^yj-E^ «5^ +

Так как ограничений на значение ошибки сети в момент окончания управления не наложено, то вариации 6E произвольные; выберем из них нулевые. Следовательно, -faCO * (Q^L^aiCos^Wtt) + ^sin^t))) +

+ u(t)) — u² (t) — F(t_t)] * St_T = 0 . (13)

Учитывая, что правый конец траектории по времени не зафиксирован, можно считать, что 5t₁ Ф 0. Произведем сокращение на эту величину.

Заменив в (13) управление на его выражение (9), получим:

-^(t) *Z™i(a, cos(w^t) + biSin^w^t)') +

+ 2^ + ^=f(tl).  (14)

Решая третье уравнение из (10), получим:

^(t) = -t + C.

где для различных моментов времени окончания управления с помощью (15) вычисляется значение константы С .

rp. -t+c

Тогда ^optW =    , подставляя которое в первое уравнение системы (10), имеем: ^ = ^+ (S^iCajCosCWit) + biSinCw.t))).(16)

Интегрируя (16), получим:

E (t) = — у H-----Ь — sin(Wjt) — — cosfiVj t) + C_± .(17)

где С₁ вычисляется из второго условия системы (10) при известной С .

Характер уравнения (17) говорит о том, что при некотором значении t E(t) будет равняться нулю, а далее стремиться к — CO, что противоречит физическому смыслу ошибки сети E. Поэтому управление (15) должно остановиться при E меньше, чем наперёд заданное E(t₁). В силу этих заключений будем пытаться решить поставленную задачу при замкнутом управлении.

Синтез управления с обратной связью

Рассмотрим квадратичный функционал качества управления сетью, который запишем как (5), минимизирующий любое управление, прилагаемое к нейронной сети:

I = j и² ^Е, W, t)dt + Е (W, t_v и) -^ min.(18)

Решением любой из задач управления сетью выступает оптимальное управлениеu*(^W/,t) с обратной связью, момент окончания управления ^i , а также оптимальная траектория EXt.W.u *) снижения ошибки под воздействием управления.

Кривые u*(E,W,t) и E\t,W,u *) приводят нас к способу управления, который должен быть реализован алгоритмически через элементы структуры и поведения рассматриваемой нейронной сети с переменным распространением сигнала.

Вид граничного условия (19) определяется исходя из того, что в различные моменты времени окончания управления будет существовать различный фиксированный уровень остаточной ошибки:

Ф(брЕ) = Е ^,

где Ф(ЧЛ) – функция граничного условия.

Запишем уравнение Беллмана Ф для задачи (4) с функционалом качества (5) и граничным условием (19):

фБ = ^ + ^ * ((S^iCaiCosCw.t) +

+ b,sin(w,-t))) + u(E, t)) — u²(E, t)

, (20)

Найдем производную функции Беллмана по управлению и приравняем к нулю для поиска структуры оптимального управления:

^^Б =^-2u(E,t) = 0.   (21)

Эи ЭЕ '    ?

Отсюда структура оптимального управления выражается как:

.

^v ‘ ^J 2 SE

Подставив (22) в (20), получим

a* a*

St + SE

+ b^in

* (a^i(aiCos(Wit) +

.

С учетом соображений (19) будем искать ре-

шение уравнения (23) в виде

.

Запишем, что

8Ф _ dK(t)

St

St

,

.

SE        -

Подставив (25) и (26) в (23), получим общий вид уравнения, решив которое, можно получить функцию остаточной ошибки от времени, из которой с учетом (24), (22) можно будет получить функцию управления с обратной связью:

E^t^ Ган! £(t) [dtJ

EU^

Eto

(££1(alcos(wit') +

.

При начальных условиях, т.е. E(t0)=E0=0,8777255 от максимальной амплитуды ряда ошибки и при выбранных основных гармониках с круговыми частотами 0,07; 1,05;1,48; 1,7; 2,25; 2,60; 3,25; (по дан-

ным программного продукта «SCAN» и мощности амплитуды: 0,223607; 0,3; 0,3; 0,4472; 0,4472; 0,547; 0,387 от максимальной амплитуды ряда ошибки, применение метода Рунге-Кутты 4-го порядка для уравнения (27) дало следующий вид функции управления примененной нейронной сетью.

По оси абсцисс данного графика показаны отсчёты времени.

Сделанные расчёты позволяют установить следующее:

• 1.    С ростом времени необходимая интенсивность управления сетью должна меняться также квазипериодически, согласно рис. 1.

• 2.    Увеличение учёта числа гармоник, включаемых в уравнение эволюции ошибки сети (4), приведёт к росту точности решения.

• 3.    В общем случае искусственная нейронная сеть не является полностью управляемой системой, однако приведенное решение позволяет считать нейронные сети с переменной проводимостью сигнала системами, управляемыми по выходу.

• 4.    Несмотря на найденный характер управления, возникает новая проблема трансформации найденного решения в конкретные алгоритмы, изменяющие веса связей между нейронами, скорости изменения данных весов, скорость обучения сети теми средствами, которые предусмотрены в конструкции нейронной сети [2]. Для реализации полученной кривой управления необходимо провести серию численных экспери-

График функции управления ИНС при указанных начальных условиях (численное решение)

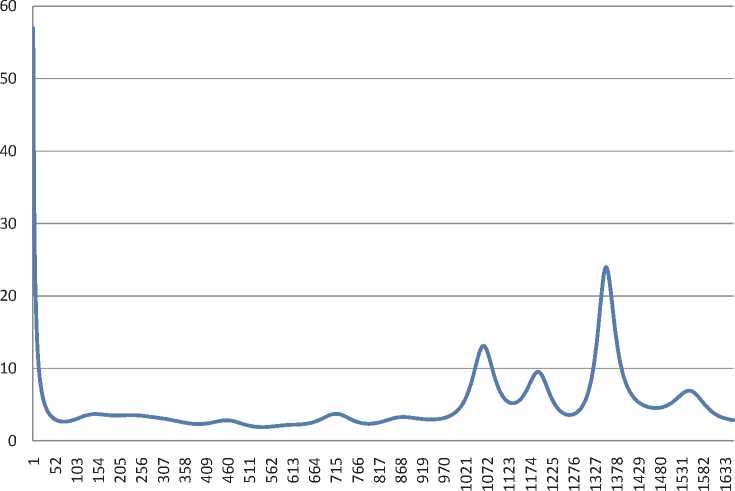
Рис. 1. Полученное решение в виде функции K(t) (согласно (22))

ментов, устанавливающих влияние поведения различных групп весов сети на спектральный состав наблюдаемых кривых ошибки ИНС с переменной проводимостью сигнала, что является направлением развития выполняемого исследования.