Управление временем в динамической имитационной модели

Богданова Е.А., Димов Э.М., Маслов О.Н., Трошин Ю.В.

В статье дано описание принципа управления временем в динамической имитационной модели, принципы построения моделирующих алгоритмов на основе выбора метода реализации механизма управления модельным временем.

Понятие модельного времени

Оценка эффективности моделируемой системы связана с временными характеристиками ее функционирования. Характерной особенностью большинства практических задач является то, что скорость протекания рассматриваемых процессов значительно ниже скорости реализации модельного эксперимента. Например, если моделируется работа вычислительного центра в течение недели, то вряд ли он будет воспроизводиться в модели в таком же масштабе времени. С другой стороны, даже те имитационные эксперименты, в которых временные параметры работы системы не учитываются, требуют для своей реализации определенных затрат времени работы компьютера.

Из сказанного выше можно отметить, что при разработке практически любой имитационной модели и планировании проведения модельных экспериментов необходимо соотносить между собой три представления времени:

• -    реальное время, в котором происходит функционирование имитируемой системы или процесса;

• -    модельное время, в масштабе которого организуется работа модели;

• -    машинное время, отражающее затраты времени ЭВМ на проведение имитации.

Модельное время – это виртуальное время, в котором автоматически упорядочиваются все моделируемые события, причем не обязательно пропорционально реальному времени, в котором развивается моделируемый процесс.

Выбор метода реализации механизма управления модельным временем зависит от назначения модели, ее сложности, характера исследуемых процессов, требуемой точности результатов и т.д. При разработке имитационной модели задаются следующие параметры модельного времени: период моделирования и шаг моделирования.

Период моделирования – это интервал времени, определяющий длительность имитируемого процесса.

Существует два метода реализации механизма управления модельным временем – с постоянным шагом и по особым состояниям (см. рис. 1).

При использовании метода постоянного шага отсчет модельного времени ведется через фиксированные, выбранные исследователем интервалы времени. События в модели считают наступившими в момент окончания этого интервала. Погрешность в измерении временных характеристик системы в этом случае зависит от величины шага моделирования Δ t .

Метод постоянного шага предпочтительнее, если:

• -    события появляются регулярно, их распределение во времени достаточно равномерно;

• -    число событий велико и моменты их появления близки;

• -    невозможно заранее определить моменты появления событий.

В данном случае механизм управления модельным временем достаточно просто реализовать, если условия появления событий всех типов в модели можно представить как функцию времени.

Выбор величины шага моделирования является нелегким и очень важным делом. Универсальной методики решения этой проблемы не существует, но во многих случаях можно использовать один из следующих подходов:

• -    принимать величину шага равной средней интенсивности возникновения событий различных типов;

• -    выбирать величину Δ t равной среднему интервалу между наиболее частыми (или наиболее важными) событиями.

При моделировании по особым состояниям модельное время каждый раз изменяется на величину, строго соответствующую интервалу времени до момента наступления очередного события.

В этом случае события обрабатываются в порядке их наступления, а одновременно наступившими считаются только те, которые являются одновременными в действительности.

Метод моделирования по особым состояниям сложнее в реализации, так как для него требуется разработка специальной процедуры планирования моментов наступления событий.

Моделирование по особым состояниям целесообразно использовать, если:

• -    события распределяются во времени неравномерно или интервалы между ними велики;

• -    предъявляются повышенные требования к точности определения моментов наступления событий во времени;

• -    необходимо реализовать квазипараллель-ную обработку одновременных событий (последовательный характер обработки событий в имитационной модели, которые в реальной системе возникают одновременно).

На рис. 1 представлен механизм управления модельным временем по принципу постоянного шага и по особым состояниям в зависимости от возникновения событий в реальном процессе. При реализации механизма постоянного шага весь период моделирования делится на равные промежутки времени Δ t - шаг моделирования. Если в реальном процессе за время Δ t было совершено событие, то на шаге Δ t проводится расчет всех параметров процесса с учетом возникновения события. В случае, когда за период Δ t совершается два события ( С ₂ , С ₃ ), то на шаге 2Δt проводится расчет параметров процесса с учетом возникновения этих двух событий. Одновременное возникновения двух событий ( С ₄ , С ₅ ) влечет за собой квазипараллельную обработку событий на шаге 3Δt . Если за шаг Δ t не произошло ни одного события, то этот промежуток времени (3 Δ t – 4 Δ t ) является пустым тактом. В этом случае по истечению времени шага моделирования (4 Δ t ) проводится перерасчет параметров процесса – пустой прогон модели.

При реализации механизма по особым состояниям расчет параметров моделируемого процесса проводится строго во время возникновения очередного события: возникновение события С ₁ – расчет параметров процесса на шаге δ t ₁ и т.д.

В итоге можно сделать два вывода.

• 1.    Выбор механизма управления модельным временем определяет и технологию реализации имитационной модели.

• 2.    Определяющим фактором, влияющим на выбор метода моделирования, является тип моделируемой системы или процесса: для дискрет-

  

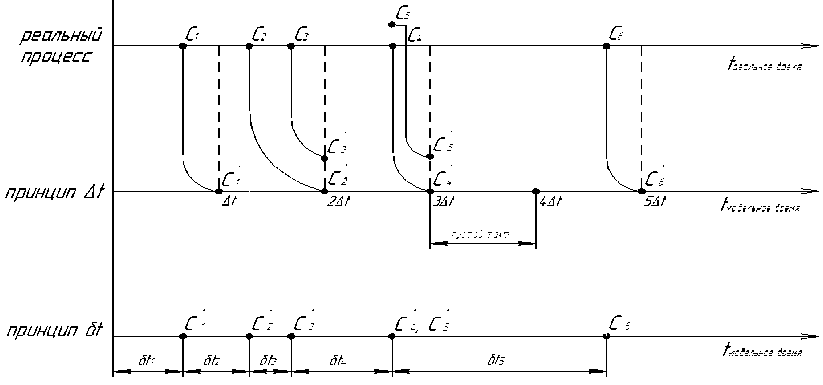
  Рис. 1. Реализация механизма продвижения модельного времени

  
  

ных систем, события в которых распределены во времени неравномерно, более удобным является изменение модельного времени по особым состояниям.

Если в модели должны быть представлены компоненты реальной системы, работа которых измеряется в разных единицах времени, то они должны быть предварительно приведены к единому масштабу.

Моделирующий алгоритм

Моделирующий алгоритм должен отражать процесс функционирования системы во всей сложности и разнообразии и, в то же время, не создавать чрезмерных трудностей при его машинной реализации и использовании [1-3]. Из этого вытекают следующие требования к моделирующему алгоритму:

• -    моделирование одновременной и независимой работы любого числа элементов системы. Естественно, что в системе в некоторый произвольный момент модельного времени t может одновременно производиться обслуживание в любом числе аппаратов, в том числе и во всех. Моделирующий алгоритм должен обеспечивать моделирование всех этих событий в один и тот же момент модельного времени;

  

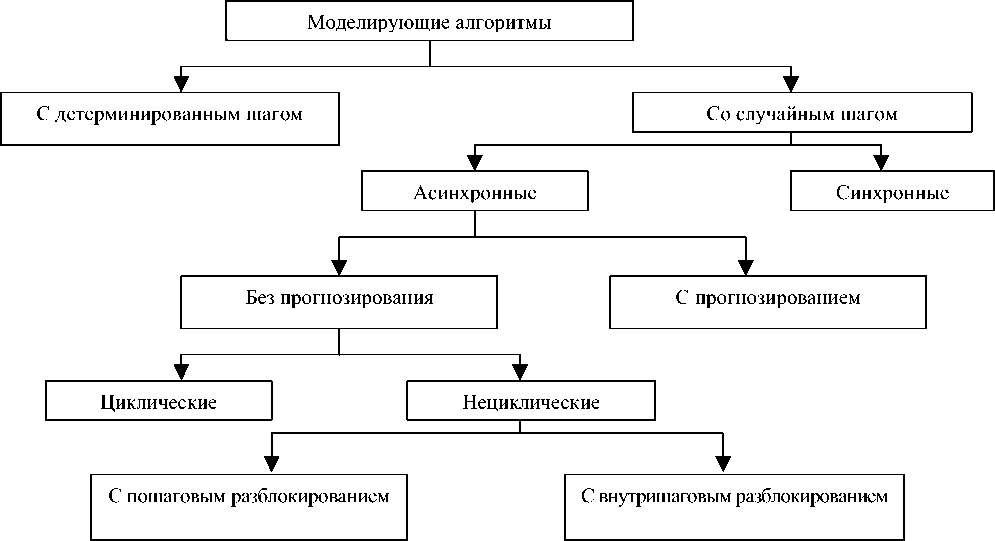
  Рис. 2. Классификация моделирующих алгоритмов СМО

  
  

• -    универсальность относительно структуры системы или процесса.Структура системы может быть любой степени сложности;

• -    незначительные затраты памяти и машинного времени на моделирование;

• -    простота логики алгоритма,возможность разбиения его на автономные блоки,позволяющие независимое программирование и отладку,простота внесения изменений в алгоритм, максимальная стандартизация алгоритма.

Большое разнообразие СМО потребовало разработки моделирующих алгоритмов различных типов. Классификация их носит в известной мере условный характер (см.рис. 2),так как при моделировании работы сложной системы возможно сочетание элементов различных алгоритмов.Моделирующие алгоритмы СМО делятся на алгоритмы с детерминированным и случайным шагом, которые соответственно реализуют способы моделирования «с постоянным шагом Δ t » или «по особым состояниям».

Описание моделирующих алгоритмов

Процесс функционирования системы массового обслуживания в течение некоторого интервала времени T можно представить как случайную последоват ельн ость дискретных моментов времени t n ( n = 0, N ) . В каждый из этих моментов происходят изменения состояния одного или нескольких элементов системы, а в промежутке между этими моментами никаких изменений состояния системы не происходит [4].

В моделирующем алгоритме должно выполняться следующее рекуррентное правило: событие, происходящее в момент t _n только после того, как промоделированы все события, происшедшие в момент t _v В противном случае результат моделирования может оказаться неверным.

В моделирующем алгоритме с детерминированным шагом принят следующий способ выполнения этого правила: определяется минимальная длительность обслуживания по всем аппаратам и минимальный интервал между моментами поступления требований по всем входящим потокам.Наименьшая из этих двух величин ( A t ) принимается за шаг моделирования (детерминированная величина).

Способ моделирования с детерминированным шагом состоит в следующем.

• 1.    На n -м шаге в момент t _n просматриваются состояния всех элементов системы и определяется,ка-кие элементы могут изменить свое состояние в этот момент.

• 2.    Моделируются все изменения состояния,кото-рые могут произойти в момент t _n .

• 3.    Определяется t_{n + 1} = t_n + A t , где A t - детерминированная величина: шаг моделирования,и производится переход к (n + 1) -му шагу

Как следует из определения шага моделирования, при этом гарантировано, что в промежутке между t _n+1 и t _n не произойдет никаких изменений состояния системы.

Основным недостатком алгоритма с детерминированным шагом является большое число лишних вычислений, несвязанных с изменениями состояния системы.Однако этот недостаток часто является не-существенным,так как в системах с большим числом элементов затраты на вычисления,связанные с моделированием работы системы в периоды ее неизменного состояния, относительно малы.

В моделирующих алгоритмах со случайным шагом элементы системы просматриваются только в моменты изменения состояния системы.Поэтому длительность шага Δ t представляет собой случайную величину.Моделирующие алгоритмы со случайным шагом могут быть синхронными и асинхронными.

При построении синхронного моделирующего алгоритма выбирается один из элементов системы или один из входящих потоков в качестве ведущего. Шаги моделирования будут соответствовать моментам измерения состояния ведущего элемента или моментам поступления требований ведущего входящего потока. Процесс моделирования при этом как бы «синхронизируется» этими моментами.

Использование синхронного алгоритма для моделирования системы с циклом вызывает серьезные трудности. Преодоление этих трудностей в принципе возможно,однако оно ведет к заметному усложнению алгоритма. В асинхронных моделирующих алгоритмах ведущий (синхронизирующий) элемент отсутствует,и очередному шагу моделирования может соответствовать поступление требования любого входящего потока или наступление какого-либо события. Асинхронные моделирующие алгоритмы подразделяются на алгоритмы с прогнозированием и без прогнозирования.В моделирующем алгоритме с прогнозированием очередному шагу моделирования может соответствовать только освобождение любого аппарата,то есть переход требований из него в элемент следующей фазы или появление требования любого входящего потока.В моделирующем алгоритме без прогнозирования очередному шагу моделирования соответствует момент окончания обслуживания в любом аппарате или поступление требования любого входящего потока.В этом случае нет необходимости в прогнозировании момента освобождения аппарата,так как вопрос о том, останется ли требование в аппарате после окончания

НАЧАЛО

Ввод параметра потока продолжительности остановок ATIME

Ввод параметра потока кол-ва остановок ACOUNT

Малая вероятность наступления события PCOUNT = ACOUNT / 1000

> 1000

A[I] < PCOUNT

В J-ой ячейке 1-г столбца таблицы записан 0

K меньше числа, записанного в J-ой ячейке

1-го столбца таблицы

Построение диаграммы числа остановок

__

Построение гистограммы времени остановок

31б

31в

Сохранение в формате документа

MS Word

Сохранение в формате текста *.txt

Сохранение в формате таблицы MS

Excel

POISSON = POISSON + 1

Случайное число из распределения Пуассона POISSON = 0

В J-ую ячейку 2-го столбца таблицы записать 0

Расчет общих затрат за месяц

A [ I ] = RANDOM

Запись в J-ую ячейку 1-го столбца таблицы значения POISSON

Запись в J-ую ячейку 3-го столбца таблицы значения SUM

Расчет общих затрат за год

Сохранение результатов расчетов в файл

< 100

TSTOP(K) = TSTOP / 100

TSTOP = TSTOP- LN(RANDOM) / λ

Запись в J-ую ячейку 2-го столбца таблицы значения TSTOP

( КОНЕЦ

SUM = SUM + TSTOP(K)

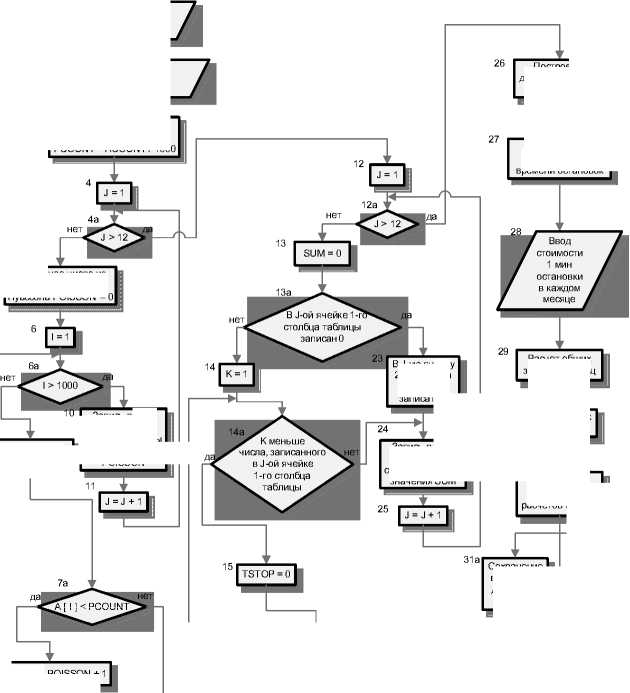
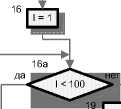
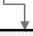
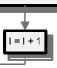
• Рис. 3. Блок-схема моделирующего алгоритма «Эксплуатировать оборудование»

обслуживания,может быть решен на последующем шаге. В нециклическим моделирующем алгоритме с пошаговым разблокированием момент выполнения очередного шага определяется как минимум из минимального времени окончания обслуживания во всех аппаратах и минимального времени поступления очередных требований во всех входящих потоках. В нециклическом моделирующем алгоритме с внутришаговым разблокированием все изменения состояния элементов системы,вызванные окончанием обслуживания в любом из аппаратов,модели-руются за один шаг. Алгоритм состоит из моделирующих блоков,каждый из которых соответствует одному элементу системы.

Формы представления моделирующих алгоритмов

Обобщенная (укрупненная) схема моделирующего алгоритма задает общий порядок действий при моделировании системы без каких-либо уточняющих деталей.Обобщенная схема показывает,что необходимо выполнить на очередном шаге модели-рования,например,обратиться к датчику случайных чисел.

Детальная схема моделирующего алгоритма содержит уточнения,отсутствующие в обобщенной схеме. Детальная схема показывает не только, что следует выполнить на очередном шаге моделирования системы,но и как это выполнить.

Логическая схема моделирующего алгоритма представляет собой логическую структуру модели процесса функционирования системы. Логическая схема указывает упорядоченную во времени последовательность логических операций, связанных с решением задачи моделирования.

Схема программы отображает порядок программной реализации моделирующего алгоритма с использованием конкретного математического обеспечения. Схема программы представляет собой интерпретацию логической схемы моделирующего алгоритма разработчиком программы на базе конкретного алгоритмического языка. Различие между этими схемами заключается в том, что логическая схема отражает логическую структуру модели процесса функционирования системы, в схеме программы – логику машинной реализации модели с использованием конкретных программно-технических средств моделирования.

Логическая схема алгоритма и схема программы могут быть выполнены как в укрупненной, так и в детальной форме [4; 6].

Пример реализации моделирующего алгоритма

На рис. 3 приведен пример детальной схемы моделирующего алгоритма имитационной модели «Эксплуатировать оборудование», разработанный применительнокпроцессуфункционированияобо-рудования регионального телерадиопередающего центра [5-6]. Данный алгоритм предназначен для прогнозирования времени остановок оборудования по различным причинам с целью определения затрат (или недополучения прибыли) предприятия по причине технических остановок оборудования.

В основе построения моделирующего алгоритма лежит метод реализации механизма уп- равления модельным временем с постоянным шагом, так как события (остановок оборудования) достаточно редки и невозможно заранее определить моменты появления событий. В соответствии с этим моделирующий алгоритм представляет собой моделирующий алгоритм с детерминированным шагом. Период моделирования составляет 1 год, шагом моделирования является 1 месяц, то есть моделируется число технических остановок в месяц для 12 месяцев в течение года.