Управление всплесками орбитального углового момента в астигматических структурированных пучках в рамках ABCD матричных преобразований

Наглядность и относительная математическая простота унитарных АВСD матричных преобразований, открытых еще в начале 70-х годов прошлого века [1, 2], оказывается сейчас наиболее удобным инструментом для инженерного моделирования сложных оптических устройств и систем на основе структурированных когерентных и частично когерентных пучков [3 – 8]. Основным элементом в этом подходе является унитарная ABCD-матрица вида

M =

f A B 1 I C D J ,

где det M = AD – BC = 1 для отдельного элемента системы, так что вся оптическая система описывается последовательным произведением этих матриц. Как правило, такие матричные преобразования используются для вычисления комплексного параметра q ( z ) фундаментального Гауссова пучка, включающего в себя радиус кривизны волнового фронта R ( z ) и радиус поперечного сечения пучка w ( z ) как 1 / q ( z ) = 1 / R ( z ) – i 2/ kw ²( z ), где k – волновое число. Однако, когда приходится работать с пучками Эрмита–Гаусса (ЭГ-), Лагерра–Гаусса (ЛГ-) или другими типами пучков высших порядков, обращаются к интегралу Коллинза [9], записанному для когерентных параксиальных пучков как

^{T (} r , z ) = Т^Гл L^ ⁽ P )exp^{{ -} i ^[ A ⁽ z ) ¹ P | 2 - m 2 n iB ( z )•”* 2 B ( z ) (1)

-2(pr) + D (z )|r|2]} d 2p, где ^(p) — комплексная амплитуда пучка на входе оптической системы, p = (^, n), r = (x, y), A(z), B(z), C(z), D(z) – элементы ABCD-матрицы.

Используя этот интеграл, Сейгман [2], а затем Бе-ленджер [10] наметили общий подход для описания единичных ЭГ- и ЛГ-пучков в простейших оптических системах, содержащих сферические линзы. Аналогичный расчет для единичного ЛГ-пучка был выполнен Таше [11]. Алиева и Бастианс [12, 13], рассматривающие пучки ЭГ- и Эрмита–Лагерра–Гаусса (ЭЛГ-) в оптических системах первого рода с каскадом линз, усилителем и ортосимплектической системой (система, которая является одновременно упрощенной и ортогональной), используют подход на основе 4×4 симплектических матриц. Преобразование ЭГ-пучков в более сложных системах – конверторах оптических вихрей, содержащих астигматические элементы, авторы статей [14, 15] применили скорее искусственный, чем стандартный ABCD-подход, в то время как Хонина и соавторы [16] рассмотрели различные типы астигматических модовых конвертеров, используя для моделирования стандартные дифракционные методы. Дело в том, что, если в оптической системе присутствуют астигматические элементы

(например, цилиндрические линзы), ее анализ значительно усложняется. Теперь любой цилиндрический пучок должен быть представлен в базисе собственных ЭГ-мод, горизонтальные и вертикальные оси которых направлены по осям цилиндрической линзы с соответствующим масштабированием координат [17 – 21], а в сложной астигматической системе они могут перепутываться.

Ситуация значительно усложняется при использовании методов ABCD-матриц для структурированных пучков, которые в настоящее время широко используются в различных областях науки и техники, требующих удобных математических подходов для проектирования оптических систем [22]. Прежде всего, это связано с тем, что в простейшем случае требуется представить ЛГ-моду в терминах ЭГ-мод в собственной системе координат цилиндрической линзы. Это выглядит так [17, 18]:

LGn ,± i (r) = n 2 n+1

= '       . z ( ± 2i) ^-p ⁿ • ^{i -} j,ⁿ - j ■«» HG 2 n- j , j ( r ).

2 n ! _{j =0}

где Pjn+l-j,n-j) (.) - многочлен Якоби. n и I - радиальное и азимутальное числа. Если оси ЭГ- мод повернуты на угол п /4 относительно оси астигматизма линзы, то следует использовать разложение в виде x + У x - Ух

^HGn , n + 1 ⁽ Г- . I— )

n 2 n + 1

= is)^ Z ² - Pj" + ^l -" - " (0) ^HG 2 n . 1 - j , j ( r ).

2 n ! _{j =0}

а ABCD-преобразование осуществляется для каждого направления x и y осей астигматического элемента.

В более сложном случае произвольной ориентации осей пучка относительно осей линз необходимо использовать громоздкие базисные преобразования, полученные Алиевой и Бастиансом [23]. Разработка оптической системы с единичным астигматическим преобразованием структурированных пучков требует применения этих базисных преобразований к каждой моде пучка, и в то же время необходимо внимательно следить за амплитудами и фазами мод, возникающих в результате преобразований. Когда речь идет об оптической системе, содержащей последовательность астигматических элементов с различной ориентацией осей, для каждого элемента следует использовать базисные преобразования. В результате основной подход к астигматическим преобразованиям структурированных пучков был сосредоточен на анализе траекторий на 2D-сфере с использованием унитарности астигматических преобразований [17, 24, 25]. Но здесь исследователь сталкивается с длинной последовательностью громоздких нестандартных вычислений, что не оптимально для инженерного моделирования. Таким образом, для инструментальной реализации устройств, преобразующих неустойчивый астигматический структурированный пучок в структурно устойчивый без потери его уникальных свойств, требуется разработка базисных методов ABCD-матриц.

В данной статье мы теоретически и экспериментально обсудим ABCD-преобразования в одной астигматической системе, которая наиболее важна для практической инженерии. Система содержит цилиндрическую линзу, формирующую всплески орбитального углового момента (ОУМ) и корректирующую сферическую линзу, позволяющую разделять астигматическую и вихревую компоненту ОУМ, а также преобразующую структурно неустойчивый астигматический структурированный пучок в устойчивый без потери его уникальных свойств.

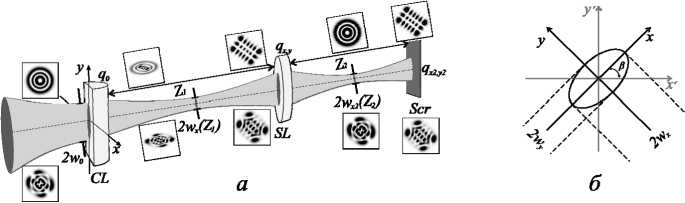
Рис. 1. (а) Эскиз астигматической системы с цилиндрической (CL) и сферической (SL) линзой; (б) взаимная ориентация поперечного сечения астигматического пучка в координатах цилиндрической линзы (x, y) и лабораторных координат (x', y')

через цилиндрическую линзу и разделении вихревого и астигматического ОУМ после корректирующей сферической линзы. Схема оптической системы показана на рис. 1а. Мы предполагаем, что структурированный sLGn,ℓ-пучок [24] с радиальным числом n, азимутальным числом ℓ и комплексным параметром q(z) = z – iz0 (где z0=kw02 /2 – длина Рэлея) падает на цилиндрическую линзу с фокусным расстоянием fx, расположенную в плоскости z = 0, так что начальный комплексный параметр равен q0=- izо и с радиусом перетяжки w0 Гауссова пучка. Сферическая линза выполняет преобразование Фурье и позволяет не только разделить вихревую и астигматическую составляющие ОУМ, но и преобразовать структурно неустойчивый пучок в структурно устойчивый без потери всплеска ОУМ при изменении параметров оптической системы. В целом, сложную оптическую систему удобно представлять в виде произведения матриц каждого оптического элемента [2]. Однако, поскольку преобразование структурированных сЛГ-пучков астигматическим элементом ранее не рассматривалось, мы сначала подробно рассмотрим преобразование сЛГ-луча на цилиндрической линзе, определив его комплексные параметры qx (z) и qy (z), а затем используем их для анализа распространения пучка через остальные оптические элементы.

2. Структура сЛГ-пучка после единственной цилиндрической линзы

В направлении x действует матрица цилиндрической линзы и смещение на длину z , которое записывается в виде

M x

/ 1

z 1 '

Откуда q x параметр получаем в виде

q x ( z ) = z 0

^{[ Z} 1 ^{( K} 2 ⁺ 1) ^-K x ] ^- i

k X + 1 x

,

где

Z 1 = —, к

z 0

. f x

Полученные результаты позволяют найти радиусы пучков для x и у направлений следующим образом

Подчеркнем, что цилиндрическая линза вводит различный масштаб по собственным координатам (x, у) (см. рис. 1 б). Предположим, что оси цилиндрической линзы и лабораторные координаты совпадают, что соответствует случаю так называемого простого астигматизма [17, 18, 19]. Поскольку ЭГ-пучки являются собственными модами астигматического элемента, представим структурированный сЛГ-пучок в терминах стандартных ЭГ-мод в выражении (2), но с различным масштабом по координатам (x, у) (см. также формулу (3.8) из монографии [19])

K (---) = —-— ^

2 q x ( z 1 )       w x ( z 1 )

w2( Z1) = wX[(1 - Z1Kx )2 + Z12],2(11)

wX( Z1) = wX(1 + Z12),2(12)

в то время как фазы Гуи мод равны [2]

г x ( Z 1 ) = arg q ^x = ¹arg(1 -k x Z 1 + iZ 1 ), (13) \ A ■ q x + B 1

Г у (Z 1)=1arg(1 + iZ1).(14)

sLG n , + _t ( r , Z 1 )

С-D n _x 2 2 n + 3 1 /2 n !

Таким образом, после подстановки (9)-(14) в выражение (4) и последующих преобразований получаем комплексную амплитуду астигматического сЛГ-(асЛГ-) пучка после цилиндрической линзы в виде

₍^Xxx_{w (} У ^x H 2 n + t - j ⁽ — ) H j ⁽ — W x ( z j w x ( z 1 )

■ ^)exp^[ ik ( '’ + "     Ц,

2 q x ( Z 1 )    q z ( Z 1 )

xx

У у

где H_n (VX x ) - многочлен Эрмита, Q_n - амплитуда ЭГ-моды, которая в рамках ABCD-правила равна [2]

О = / -------q .х;-------.n

Q x • ^У                               ) .

\ A x , у ■ q о, x , у ⁺ B x , у

Очевидно, что в общем случае нам придется использовать две группы матриц ABCD для направлений x и у , которые задают комплексные параметры

asLG n , _t ( x , у , Z 1 | e , 9 ) =

I     = x xj wx ( Z1) WУ ( Z1)

x exp{ - i [(2 n + / + 1/ 2) Г x ( Z 1 ) + Г у ( Z 1 )]} x

( - 1) n

2 2 n + 3 ^ /2 n !

^{x H} 2 n + t - j ⁽

2 n + L

^ (2 i ) ^j P (^{n + l - j}’^{n - < )}(0)(1 + e e j ⁹ ) x         (15)

j =0 ixx

W x ( Z 1 )

) H j (^7 7 ;) x ^W У ^{( Z} 1 )

x ²         у ²

x exp( ij Г xy (Z1)) exp(i[_      + - ]), qx (Z1)   qy (Z1)

A x q о ( z 1 =0) + B x = A y q о ( z 1 =0) + В у C x q 0 ( z 1 = 0) + D_x ’^qy C y q 0 ( z 1 = 0) + D y '

где Г xy ( Z 1 ) = Г v ( Z 1 )-Г x ( Z 1 ), w 0 = Xz 0 z 0 / k , x ^ x / w 0 , у ^ у / w 0 ,

Однако цилиндрическая линза не изменяет масштаб в направлении у , то есть в области (0, z 1 ), и мы можем написать

q y ( z 1 ) = z 1 - iz 0 .

q x ( z 1 ) =

^{[ Z} 1^{( k X +} 1) ^-K x ] ^- i K x + 1

Заметим, что комплексная амплитуда (15) совпадает с амплитудой, полученной Бекшаевым и др. в работе [26] для простейшего случая с нулевым радиальным

числом n =0. Компьютерное моделирование и экспериментальные результаты эволюции картин интенсивности ( а – в ) стандартной ЛГ-моды и ( г – е ) сЛГ-пучка вдоль направления распространения Z 1 показаны на рис. 2. Как и ожидалось, ЛГ-пучок (рис. 2 а ) преобразуется в ЭГ-пучок на длине z 1 =2 f x ( Z 1 = 1), а количество нулей интенсивности вдоль осей x и y позволяет определить топологический заряд ЛГ-пучка [27, 28]. Эволюция картины интенсивности структурированного пучка иллюстрирует по крайней мере один интересный эффект (рис. 2 г ). Вблизи Z 1 = 1 картина интенсивности асЛГ-пучка превращается в почти типичную картину

ЭГ-моды. Однако, как мы покажем ниже, OУM пучка испытывает резкий всплеск. Следует также отметить, что полученные результаты хорошо согласуются с картинами интенсивности, полученными методом интегральных преобразований в статье [24]. Однако метод интегральных преобразований позволяет получать достоверные результаты только в дальней зоне дифракции или в плоскости двойного фокуса цилиндрической линзы. В то же время представленные результаты, основанные на матричном ABCD-подходе, значительно упрощают вычисления, приводящие к оптимальной форме комплексной амплитуды.

лг

Рис. 2. Распределение интенсивности: (а,г) теория и (в,е) эксперимент, (б, д) фазы, эволюции ЛГ- (а-в) n = 2, ℓ = 3 и астигматического сЛГ- (г-е) n = 10, ℓ = 1, ε = 1, θ = 0,99 π пучка, с z 0 = 1 м, f x = 0,5 м

3.    Преобразования ОУМ сЛГ-пучка после цилиндрической линзы

Орбитальный угловой момент структурированного пучка в базисе ЭГ-мод удобно представить как

L z = sJ^ C r )( x d y - y d x Ж r ) dxdy .          (17)

Очевидно, что основной вклад в OУM вносят амплитуды мод, которые мы находим из выражения (15) в виде cj(z1)=

= (2 i ) j P jn ^{+ l} - j, n ^{- < )} (0)(1 + e e i ⁶ ) exp(ij Г xy ( z )).

Чтобы найти удельный OУM, вычислим поток энергии в направлении распространения пучка по формуле

Sz = j T, r Ж( r) dxdy,(19)

так что удельный OУM равен

Iz = Lz / Sz.(20)

Используя выражения (17–20), получаем

2 n + < - 1

Lz =22n+ln ^ (j +1)!(2n + /- j)!3(Cj+1 c*),(21)

j =0

2 n + e

Sz =22 n+f-1 n^ j !(2 n + / - j)! CjC *j.(22)

j =0

Мы обнаружили, что полученные выражения могут быть сведены к выражениям (8), полученным Котляром и др. в [27], несмотря на то, что в их расчетах масштабирование комплексной амплитуды одинаково по осям x и y. Полученные результаты для ОУМ представлены на рис. 3 в виде быстрых осцилляций OУM при изменении управляющего параметра θ в различных поперечных сечениях Z1 пучка. Мы видим возникновение и подавление быстрых осцилляций OУM по мере смещения Z1 вдоль пучка, в то время как вблизи θ = 0,98π зарождается и растет всплеск OУM. Второй всплеск OУM с противоположным знаком возникает вблизи θ = 1,02π. Важно, что OУM при Z1 = 1 хорошо согласуется с результатами нашей работы [24], использующей метод интегральных преобразований, но ABCD матричный метод позволяет проследить эволюцию быстрых осцилляций и всплесков OУM по всей длине Z1 пучка. Мы также видим, что всплески OУM незначительно изменяются в дальнейшей зоне дифракции. Такое сохранение максимума всплеска OУM наглядно проиллюстрировано на рис. 4а. ОУМ достигает своего максимального значения при Z1 = 1, не- смотря на то, что картина интенсивности пучка значительно деформирована (см. рис. 4б – д), в то время как ОУМ стремится к половине радиального числа ℓz → n /2 в дальней зоне дифракции.

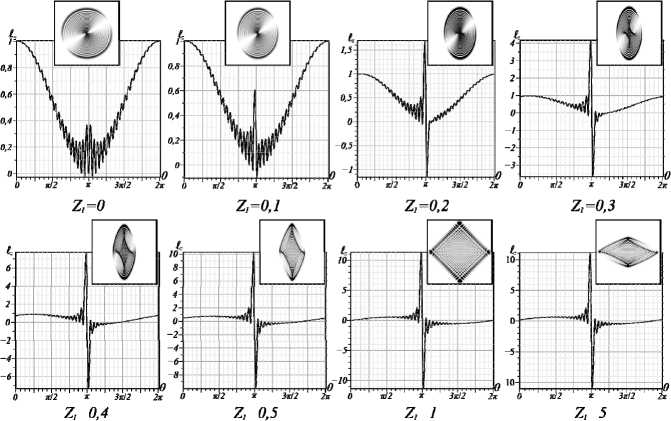
Рис. 3. Осцилляции ОУМ ℓ z ( θ ) при вариации θ -управляющего параметра асЛГ-пучка с n = 20, ℓ = 1, ε = 1 на различных длинах пучка Z 1 . Выноски: картины интенсивности для первого всплеска ОУМ

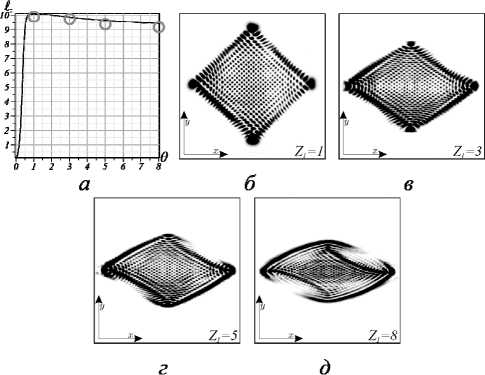
Рис. 4. (а) ОУМ ℓ z (Z 1 ) вдоль асЛГ-пучка с n = 20, ℓ = 1, z 0 = 1 м, ε = 1, θ = 0,098 π ; (б)-(д) картины интенсивности в различных сечениях пучка

сто проанализируем условия разделения вихревой и астигматической составляющих на основе ABCD матричного подхода.

Стоит отметить, что согласование радиусов пучков w x = w y происходит и в плоскости двойного фокуса цилиндрической линзы, однако здесь не происходит разделения ОУМ на вихревую и астигматическую составляющие. Для этого необходимо также согласование Г x и Г y фаз. Эту операцию делает сферическая линза при условии, что она выполняет Фурье-преобразование. Это значит, что плоскость наблюдения преобразованного пучка после цилиндрической линзы должна располагаться в плоскости заднего фокуса сферической линзы, как показано на рис. 1. Для расчета мы используем матрицу (8), в которой выполняется замена f x → f sh , z → z 2 . Тогда q x – комплексный параметр пучка определяется по рекуррентной формуле

4.    Цилиндрическая и корректирующая сферическая линза

Еще в начале 90-х годов Ананьев и Бекшаев предсказали в [29], что ОУМ сингулярного пучка имеет астигматическую и вихревую составляющие, которые можно разделеить с помощью обычной сферической линзы в плоскости, где радиусы wx и wy сфокусированного пучка вдоль направлений x и y становятся одинаковыми. Их анализ был основан на методе моментов интенсивности второго порядка. В дальнейшем этот подход был реализован для анализа как простых [21], так и структурированных сингулярных пучков [30]. В этом параграфе мы не будем углубляться в математику моментов интенсивности, а про- z0 qx qx2=                  + z0Z2=z0qx2,

- ( z 0 f sh ) q_x + 1

где

1 + i [ Z 1 + κ x ( - 1 + Z 1 κ x )] q_x =, ^x            1 +κ ² x

(24) q + Z 2 [ -κ sh q + 1]

q x 2                                ,

• 1    -κ sh q_x

и κ sh = z 0 / f sh , Z 2 = z 2 / z 0 . Теперь находим x -радиус асЛГ-пучка следующим образом

¹= -ℜ ( ^ik )= - ¹ ℜ ( ⁱ ).                 (25)

w x ² 2 2 q x 2 w 0 ² q x 2

а x -фазу Гуи определяем как [2]

Γ x 2 =arg     .

q_{x 2}

условием является требование к положению сферической линзы

Из правила ABCD находим q v комплексный параметр

q y 2

(1 - Z 2 κ sh )( Z 1 - i ) + Z 2

1 + i κ sh ( iZ 1 + 1)

= z 0 q_{y 2} ,

радиус w y и фазу Гуи

¹= -ℜ ( ^ik ) w y ² 2         2 q y 2

-

¹ ℜ ( ⁱ ), w ₀2     q_{y 2}

Γ y 2 = arg(

1 _). q y 2

Теперь комплексная амплитуда пучка записывает-

ся в виде

asLG n , _t ( x , y , z | e , 0 ) =

× wx2(z)wy2(z)

n

X exp{ - i [(2 n + / + 1/ 2) Г x ( z ) / 2 + Г ( z ) / 2]} ^ n ^ x

2 n + _t                                               n (30)

X £ (2i) j Pn+t-j,n-j) (0)(1 + eei0) exp(ijГ k 2 (z)) x j=0

xH2 n+t—j (2L__) h, (2UL) exp(i[     ; J_ ]), wx2(z)     wy2(z)        qx2(z) qy2(z)

где Г k 2 = Г x 2 – Г y 2 .

Кривые на рис. 5 определяют условия, при которых происходит разделение вихревой и астигматической составляющих OУM, а также преобразование неустойчивого асЛГ-пучка в устойчивый пучок. Кривые ( а , г ) задают условия w x ( Z 1 , Z 2 )= w y ( Z 1 , Z 2 ), при которых астигматическая составляющая ОУМ исчезает и только вихревая составляющая вносит основной вклад в OУM [21]. Можно показать, что эти условия выполняются при любом соотношении фокусных расстояний цилиндрических и сферических линз. Однако это не означает, что асЛГ-пучок становится структурно устойчивым после сферической линзы. Все же необходимо выполнить два дополнительных условия. Первое из них требует, чтобы разница между радиусами в направлениях x и y w x ( Z 1 , Z 2 )– w y ( Z 1 , Z 2 )= const оставалась неизменной, как показано на рис. 5 б , д . Это требование накладывает ограничение на неизменность астигматического компонента при прохождении через сферическую линзу (см. рис. 5 в , е ). Например, условия структурной устойчивости выполняются для всех пучков с параметрами, указанными на рис. 5 г – е , однако структурно устойчивые пучки с параметрами, указанными на рис. 5 в , е Z 2 >> 1, не допускают супервсплесков ОУМ (см. также рис. 6 и рис. 7). Вторым дополнительным

Z 1 =2 f x + f sh ,

что выполняется для кривых на рис. 5 е . Теперь посмотрим, как преобразуются всплески OУM после корректирующей линзы.

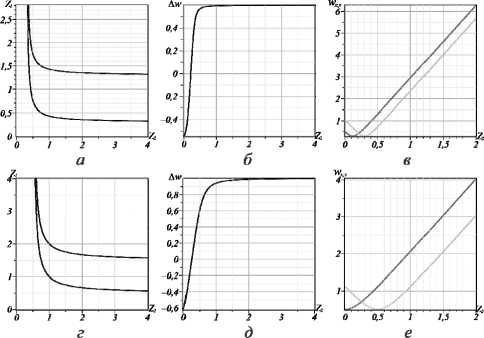
Рис. 5. Теоретические зависимости (а, г)

w x (Z 1 , Z 2 ) = w y (Z 1 , Z 2 ); (б, д) Δ w = w x – w y ; (в – е) w x (Z 2 ) (темная кривая), w y (Z 2 ) (светлая кривая), для различных фокусных расстояний: (а – в) – f x = 0,5 и f sh = 0,3; (г – е) – f x = 0,5 и f sh = 0,3; (б, в) – Z 1 = 0,3, (д, е) – Z 1 = 0,5; (а – е) – z 0 = 1 м

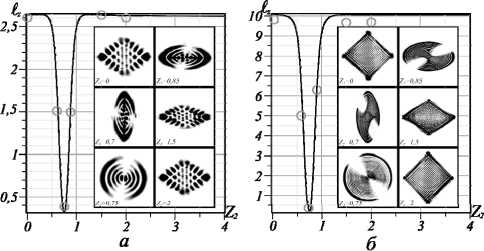
Рис. 6. Зависимость ОУМ ℓ z ( θ ) от управляющего параметра θ асЛГ-пучка с (а) n = 4, ℓ = 1, (б) n = 20, ℓ = 1 на длине Z 1 = 2f x + f sh м, f x = 0,5 м, z 0 = 1 м

5. ОУМ сЛГ-пучка после корректирующей линзы

Для того чтобы рассчитать OУM, мы используем описанный выше подход. Для этого достаточно записать амплитуды ЭГ-мод из уравнения (30) в виде

C j ( z i , z 2 ) = (2 i ) ^j P j^{n + < - j},^{n - j )}(0) x × (1 +ε e ^{ij θ} )exp( ij Γ k 2 ( z 1 , z 2 )).

После подстановки уравнения (30) в уравнения (21) и (22) получаем OУM на фотон в виде многопараметрической функции ℓ z = ℓ z ( Z 1 , Z 2 , f x , f sh , ε , θ , n , ℓ ). Мы сосредоточимся на оптической системе, в которой сферическая линза расположена в соответствии с условием (31). Рассмотрим особые точки в зависимости OУM ℓ z ( Z 2 ) от смещения вдоль асЛГ-пучка в состоянии с малым n =4 и большим n =20 радиальными

числами и минимальным азимутальным числом ℓ = 1, в то время как фазовый параметр θ соответствует всплеску ОУМ в двойном фокусе Z 1 =2 f x асЛГ-пучка. Кривая OУM на рис. 6, окруженная картинами интенсивности, имеет резкий провал в точках w x = w y : ( a ) Z 2 =0,74, n =4, ℓ = 1 и ( б ) Z 2 =0,74, n =20, ℓ = 1, соответствующих условию коррекции астигматического пучка. Сферическая линза, выполняющая преобразование Фурье пучка со всплеском OУM превращает асЛГ-пучок в неастигматический пучок сЛГ-, соответствующий пучку на входе цилиндрической линзы. Как известно [24], максимум ОУМ в структурированном сЛГ-пучке не может превышать азимутальное число ℓ = 1, в то время как максимальный OУM астигматического асЛГ-пучка превышает половину радиального числа ℓ >  n /2. Ширина провала OУM зависит от фокусного расстояния f sh и быстро уменьшается с уменьшением фокусного расстояния. Затем

OУM резко возрастает до своего первоначального значения, и его величина не меняется при смещении плоскости наблюдения вдоль пучка, его структура интенсивности также не меняется. Пучок становится структурно устойчивым вплоть до масштабирования и вращения. Структурная стабильность распространяется как на быстрые колебания, так и на всплески ОУМ. На рис. 7 показаны изменения формы осцилляций OУM вдоль пучка после сферической линзы. Если непосредственно за сферической линзой форма осцилляций ОУМ точно соответствует колебаниям в плоскости двойного фокуса цилиндрической линзы, то в плоскости согласования x и y радиусов пучков характер осцилляций резко меняется и принимает форму осцилляций ОУМ перед астигматическими преобразованиями [24]. Небольшое смещение от этой плоскости вдоль пучка возвращает форму осцилляций к исходной форме, содержащей всплески ОУМ.

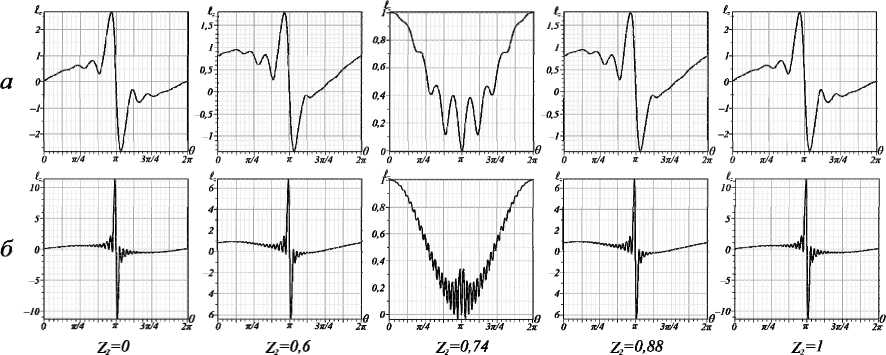
Рис. 7. Эволюция всплесков ОУМ асЛГ-пучка с (а) n = 4, ℓ = 1, θ c = 0,98 π и (б) n = 20, ℓ = 1, θ c = 0,99 π после корректирующей сферической линзы (f sh = 0,5 м, z 0 = 1 м, Z 1 = 2f x + f sh ). Выноски: картины интенсивности, соответствующие характерным областям (указанных на рисунке) всплесков ОУМ

Выводы

Использование ABCD матричного подхода, рассмотренного в статье, значительно упростило и расширило математическое описание астигматических преобразований структурированных пучков по сравнению с интегральными преобразованиями [24]. Мы продемонстрировали эффективность использования матриц ABCD для преобразования ЭГ-мод высокого порядка в структурированных сЛГ-пучках. Было показано, что астигматическое преобразование приводит к возникновению всплесков OУM, амплитуда которых превышает половину радиального числа асЛГ-пучка с минимальным азимутальным числом. Более того, в отличие от метода интегральных преобразований, мы продемонстрировали эволюцию тонкой структуры интенсивности и OУM по всей длине пучка. Было показано, что OУM незначительно изменяется в дальней области дифракции цилиндрической линзы, несмотря на то, что сЛГ-пучок теряет свою структурную устойчивость.

Исследуя трансформацию асЛГ-пучка в системе цилиндрических и сферических линз, мы не только подтвердили предсказание Ананьева и Бекшаева о разделении вихревой и астигматической составляющих OУM после сферической линзы [21], но и показали, что сферическая линза способна превратить структурно неустойчивый асЛГ-пучок в структурно устойчивый в дальней области дифракции сферической линзы при условии, что сферическая линза выполняет преобразование Фурье асЛГ-пучка в двойном фокусе цилиндрической линзы. Мы обнаружили, что в асЛГ-пучке наблюдается резкий провал OУM, где радиусы пучков wx(Z2) = wy(Z2) совпадают, что соответствует подавлению астигматической составляющей OУM, так что основной вклад в OУM вносят оптические вихри пучка. Корректируемый пучок преобразуется в свою первоначальную форму сЛГ-пучка перед астигматическим преобразованием. Небольшое смещение плоскости наблюдения из этой области приводит к резкому увеличению ОУМ. Астигматический пучок становится структурно устойчивым вплоть до масштабирования и вращения, сохраняя при этом форму осцилляций и всплесков OУM. Экспериментальные исследования хорошо согласуются с нашим компьютерным моделированием.

Авторы благодарят Е.Г. Абрамочкина за полезную дискуссию.