Упрощение уравнений движения для несжимаемой жидкости методом асимптотических разложений

Рассматриваются уравнение неразрывности и уравнения движения для несжимаемой жидкости, обтекающей вогнутую поверхность:

д u    d v

----+ ----+ -----= 0 ; d x    d y

,du   du   du    du. „ dP    .d2u  d2u p (—+u—+v—+w—) = F--+p(—- +—-+—-);

dt   dx   dy   dz dx    dx2  dy dv   dv   dv   dv. „ SP   S2 v дг v d2 v.

p (--+ u--+ v--+ w ) = F---+ p( 7 +--?+?);

d t    e x    d y    d z     ’ d y    d x ² d y ² d z ²

,dw  d w   d w   d w.  _ d P   .d ² w d ² w d ² w.

p (— + u —+ v —+ w —) = F z --+ u ( —- +—-+—-).

d t    d x    d y    d z d z     d x ²   B y    d zz

При асимптотическом анализе будем использовать ставшие уже традиционными при построении асимптотических теорий обозначения для различных областей возмущенного течения (рис. 1):

Область I – возмущенная часть внешнего невязкого течения, ее характерная толщина

А у 1 >  5 ~ О(е).

Область II – основная часть пограничного слоя с характерной толщиной

А у 2 ~ 5.

Вязкая пристеночная область III с характерной толщиной

∆ y 3 < δ.

При построении асимптотической теории вихрей Гертлера [1] в пограничном слое жидкости будем предполагать, что потеря устойчивости основного плоского течения вблизи вогнутой поверхности вызывает нелинейные возмущения функций течения в области их локализации, например

А и ~ и .

Следовательно, возмущения от вихрей уже в первом приближении влияют на характеристики основного плоского течения вблизи вогнутой поверхности. В поле центробежных сил тогда возникают возмущения давления

АP ~ ku 2 Ау, которые индуцируют поперечные составляющие скорости:

w ~ А w ~ А P ^1/1 ~ к ^1/1 и А у ^.

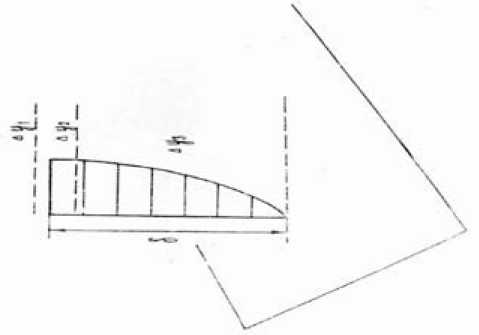
Рис. 1. Асимптотические области разложения

Так как оценки для P и w получаются из сопоставления порядков величин конвективных членов уравнений (1), то очевидно, что механизмы конвекции являются основными в процессе порождения вторичного вихревого течения.

Пусть возмущения зарождаются в области с характерной толщиной в виде

Ay ~ О (a) < 5 ~ О (е), т. е. толщиной меньшей, чем толщина пограничного слоя, расположенного непосредственно около вогнутой поверхности, где завихренность основного плоского течения вблизи вогнутой поверхности наибольшая, а функции течения изменяются пропорционально расстоянию от поверхности, например u ~ ∆y ∕ ε.

Тогда справедливы следующие оценки для функций течения:

u ~ O(a /г), \P O ( N а г ) , w ~ O ( N ^1/2 a ^3/2 /е) . (2)

Принимая, что в общем случае толщина возмущенной области «а» соизмерима с ее шириной – ∆z ~ O(c) ~ O(a), и приравнивая порядки величин членов уравнения неразрывности, можно получить, что a~c~O (Nb2),

где «а», «b» и «с» - характерные толщина, протяженность и ширина пространственной возмущенной вихревой области течения, и е 2< a < c < b < 1.

Соотношения (2) и (3) позволяют оценить порядки величин конвективных и основных диссипативных членов уравнений движения:

u ⋅ ∂ u ~ O(ℵ2b3⁄ε),ε 2 ⋅ ∂ 2u   ~ O(ε⁄ℵb2).

д x ' ^z             d y ²

Из этих оценок видно, что в наименее вырожденном случае, когда механизмы конвекции и диссипации равнозначны и u

∂u∂x

~ ε

_∂ 2 _u

∂ y ²

протяженность возмущенной области «b» по порядку величины равна b ~ O (ey5N3/5) < 1.

Оценки (2), (3) и (4) позволяют для возмущенной вихревой области течения III с характерными размерами:

Ax ~ O(b )~ О(е/ N ) ³/⁵ ,

Ay ~ Az ~ O(a) ~ O(c) ~ 0(е6/5/ N1/5), расположенной непосредственно около вогнутой поверхности, ввести следующие переменные и асимптотические разложения функций течения:

x=(     к,-,) X■ y (8  'к   ) Y3 , z - (8-5/ к 1/5 ) Z, , к »)u+^,                                                 5 V - к 1/5 8 4/5 У3+ 3        , W - к 1/5 8 4/5 W3 + ..., др = к 2/5 88/5 Рз +__ где возмущение давления Р отсчитывается от значения на вогнутой поверхности в точке зарождения неустойчивости основного плоского течения вблизи вогнутой поверхности.

Теперь подставим разложения (5) в систему уравнений (1) и совершим предельный переход

при ε → 0, ε : К < 1. Тогда получим, что в первом приближении для области III справедли- вы параболизированные в продольном направлении уравнения Навье–Стокса без продольного градиента давления:

∂ U 3 +∂ ϑ 3 + ∂ w 3 =Ο д X 3   д Y  d z 3     , ∂ U    ∂ U     ∂ U ∂ 2 U  ∂ 2 U U 3 ∂ X 3 3 + ϑ 3 ∂ Y 3 3 + w 3 ∂ Ζ 33 = ∂ Y 233 +∂ Ζ 233,                                     (6) U ∂ ϑ 3 + ϑ ∂ ϑ 3 + w ∂ ϑ 3 +Κ U 23 + ∂ ρ 3 = ∂ 2 ϑ 3 + ∂ 2 ϑ 3, д X 3     д Y 3     dZ 3          д Y  д Y 3   dz 2 ∂ w    ∂ w    ∂ w  ∂ ρ ∂ w  ∂ w U 3 + ϑ 3 + w 3 +    3 =     3 +     3 . 3 д X 3    3 д Y 3    3 д 2 з    д 2 з    д Y 23    d Z 23

На вогнутой поверхности должны выполняться обычные условия прилипания и непро-текания:

U ; = 9 3 = w 3 = O,      Y 3 - O.

Внешние и начальные краевые условия получаются из сращивания с решением для пристеночной части основного плоского течения вблизи вогнутой поверхности (с нижней сдвиговой частью пограничного слоя около вогнутой поверхности):

U , — AY 3 ,   Р з — - KA ² Y 3 ,

9з, w 3 —— O, Xз, Y3 ——^, где «А» - напряжение трения в продольном направлении на вогнутой поверхности в точке зарождения неустойчивости основного плоского течения вблизи вогнутой поверхности.

Предполагается исследовать периодические по поперечной координате «Z» – решения, поэтому

f ( X 3 , Y 3 , Z 3 ) = f ( X 3 , Y 3 , Z 3 + Z);                                                         (9)

f = U3,83, w 3,P3, где λ – длина волны вытянутых в продольном направлении стационарных вихрей Гертлера.

Краевая задача (6)–(9) описывает эволюционное нелинейное развитие вихрей Гертлера с длиной волны, меньшей толщины пограничного слоя около вогнутой поверхности. Из характеристик основного плоского течения вблизи вогнутой поверхности в краевую задачу (6)–(9) входит только величина «А». Так как протяженность исследуемой области течения мала (как видно из формулы 4), то здесь несущественно продольное изменение функций течения в основном плоском течении вблизи вогнутой поверхности, которое происходит на характерной длине Х = 0(1). Фактически же развитие коротковолновых возмущений происходит в плоскопараллельном потоке.

Таким образом, разработаны асимптотические методы решения уравнений Навье–Стокса для вязкой несжимаемой жидкости. Перспективные решения могут найти также теоретическое и практическое применение в таких областях, как исследование динамики селевых и оползневых течений, в межлопаточных каналах и гидравлических процессах.