Упрощенная методика проверки нормальности распределения статистической совокупности на основании показателей асимметрии и эксцесса в среде Microsoft Word

На практике нередко характеристики эмпирических статистических рядов рассчитывают в предположении, что ряды распределены по нормальному закону без должного обоснования этой гипотезы, так как этот закон распределения наиболее распространен и детально разработан. Вместе с тем такое обоснование должно является необходимым этапом при рассмотрении эмпирических совокупностей, что позволит избежать весьма серьезных ошибок.

Наиболее просто проверить исходную статистическую совокупность на нормальность можно на основании показателей асимметрии и эксцесса, по значениям которых судят о близости распределения статистической совокупности к нормальному закону, что бывает существенно важно при оценке результатов корреляционного и регрессионного анализа и вероятностной оценки прогнозов.

Если распределение можно считать нормальным, то характеристики, рассчитанные на основании этой статистической совокупности, будут достоверными. Если же фактическое распределение не удовлетворяет требованиям к асимметрии и эксцессу нормального распределения, то необходимо применить более мощные критерии.

При нормальном распределении показатели асимме- трии и эксцесса равны нулю, поэтому задача сводится к определению показателей (коэффициентов) асимметрии и эксцесса я оценки фактического ряда распределения.

Эмпирические коэффициенты асимметрии и эксцесса определяются по формулам: m3

m4 ств

ек =

“s — 3 "в

где m3 и m4 — центральные эмпирические моменты тре- тьего и четвертого порядков; <7g — эмпирическое среднее квадратное отклонение случайной величины от ее среднего значения.

Ограничиваясь в дальнейшем рассмотрением равноотстоящих вариационных рядов с постоянным шагом h (шаг равен разности между любыми двумя соседними вариантами ряда) удобно вычислять эти моменты методом сумм по формулам:

_ м;-зм;м;+2(м;)3 тз -

М;-4М;Мз+6(М1*)2М2-3(М1*)4

где м —        — условные моменты k -го порядка;

II ■ = ——-

' h условная варианта: xi — первоначальная варианта; С — ложный ноль — варианта, имеющая наибольшую частоту либо любая варианта, расположенная примерно в середине вариационного ряда.

При совместном использовании метода сумм и метода условного нуля условные моменты вычисляют по формулам:

d

Ml

M^

п

8г + 252

П

м; =

п d^+6d2 + 6d3

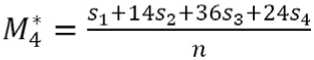
где di=ai–bi, si=ai+bi где ai, bi — накопленные частоты первой и второй половины вариантов эмпирического ряда.

Дальнейшее рассмотрение методики вычисления параметров фактического ряда рассмотрим на конкретном при- мере расчета асимметрии и эксцесса для эмпирического ряда объемом n=100 заданного в таблице-закладке 1, в первой строке которой указаны варианты ряда, а во второй — частоты вариант.

Таблица 1

Вариант, хi	48	52	56	60	64	68	72	76	80	84
Частота, ni	2	4	6	8	12	30	18	8	7	5

Исходные данные в таблицу 1 вводятся вручную непо- средственно с клавиатуры, а затем ее превращают в закладку.

Вычисления асимптоты и эксцесса начинают с определения накопленных частот , которые вычисляют в таблице закладке 2, исходные данные в которую вводятся автоматически при пуске программы на вычисления. При вычислении в таблице 2 необходимо иметь в виду, что в качестве условного нуля переменой величины принимается варианта фактического ряда, которая стоит на шестом месте .Это же место будет занимать условный ноль и при выполнении любого другого расчета с другими исходными данными.

Для запуска программы на вычисление производят щелчком по маркеру ее (по маленькому квадрату, расположенном в верхнем левом углу таблицы), а затем нажимают клавишу «F9». Далее в автоматическом режиме выполняется вычислительная программа, записанной в ячейках ее в символах вычислительного процессора MicrosoftWord. После выполнения вычислений, предусмотренных в таблице-программе 2, таблица принимает нижеприведенный вид.

В ячейках второй строки последней строки «Итого» будут указаны накопленные частоты: в верней строке — величины b_i , а в строке «Итого» — величины a_i , которые используются в виде исходных данных для дальнейшего расчета.

Далее вычисляют искомые параметры асимметрии и эксцесса по программе, записанной в таблице 3, в которой одновременно с характеристиками эмпирического ряда вычисляют выборочную среднюю величину –xВ, среднее квадратическое отклонение σВ и величины ошибок оценки асимметрии σА и эксцесса σЕ по формулам:

Хв = М, /1 + С

<7_В = м = >ж-ю²№

О" д ^  ^^^^^^^^^^~

А (п+1)(п+3)

I 24п(п-2)(п-3)

dir ^  ^^^^^”^^"————^— “ ь (п+1)2(п+3)(п+5)

Таблица 2.

Вычисление накопленных частот ai , bi
x i	n i	b1=72,00	b2=70,00	b3=42,00	b4=14,00
48,00	2,00	2,00	2,00	2,00	2,00
52,00	4,00	6,00	8,00	10,00	12,00
56,00	6,00	12,00	20,00	30,00	0,00
60,00	8,00	20,00	40,00	0,00	0,00
64,00	12,00	32,00	0,00	0,00	0,00
68,00	30,00	0,00	0,00	0,00	0,00
72,00	18,00	38,00	0,00	0,00	0,00
76,00	8,00	20,00	37,00	0,00	0,00
80,00	7,00	12,00	17,00	22,00	0,00
84,00	5,00	5,00	5,00	5,00	5,00
Итого	n =100,00	a1=75,00	a2=59,00	a3=27,00	a4=5,00

Таблица 3

Вычисление параметров асимметрии и эксцесса
Объем выборки, n	100	Шаг между вариантами, h		4,00
Величины d i		d1=3,00	d1=-11,00	d1=-15,00
Величины s i	s1=147,00	s2=129,00	s3=69,00	s4=19,00
Условные моменты, М‘к	M1*=0,03	M2*=4,05	M3*=-1,53	M4*=48,93
Эмпирические моменты 3 4 порядков, mi			m3=-121,24	m4=12578,68
Выборочная средняя,				68,12
Среднее эмпирическое квадратическое отклонение, (7g				8,05
Асимметрия, as				-0,23
Эксцесс, ek				0,00
Средняя квадратическая ошибка асимметрии, Од				0,24
Средняя квадратическая ошибка эксцесса, ^Е				0,45

В заключении расчета проводят оценку гипотезы о том, что эмпирическая совокупность имеет нормальное распределение. Проверка проводится в два этапа.

На первом этапе проверяют выполнение следующих неравенств:

ksl < l,5aA

ek ^--< 1>5сте

К    71 + 11          Ь

Если выполняются оба эти неравенства, то гипотеза о нормальном распределении фактического ряда не отвергается.

На втором этапе проверяют выполнение других неравенств:

|as| > 2ак ек Н--> 2аЕ I к п+1       £

Если выполняется хотя бы одно из этих неравенств, то гипотезу о нормальном распределении фактического ряда неравенств отвергают.

В других случаях нужна дополнительная проверка с помощью боле мощных критериев, например, методом Пирсона, методом спрямления диаграмм и т.д.

Поверка первой пары соотношений имеет вид:

|a_s| <  1,5ст_а |-0,23| < 1,5 * 0,24=0.36

Так как оба соотношения выполняются, то гипотеза о нормальном распределении не отвергается (принимается).

На этом проверка нормальности распределения фактического ряда завершается. Заключительную часть оценки гипотезы о нормальном распределении заданной статистической совокупности при необходимости тоже можно запрограммировать, но в дидактических целях это не сделано, так как пользователь компьютера не должен забывать, что за достоверность этой проверки отвечает он, а не компьютер.

Разработанная программа проверки нормальности распределения статистических совокупностей с использованием вычислительного процессора пакета прикладных программ MicrosoftWord и таблиц-закладок существенно расширяет область применения указанного пакета. Использование таблиц-закладок существенно снижает трудоемкость ввода исходных данных и результатов промежуточных результатов расчета, практически устраняя вероятность ошибок ввода исходных данных, так как их записывают только в таблицу исходных данных, а далее от таблицы к таблице данные и результаты промежуточных расчетов передаются автоматически. Более того исходные данные могут передаваться в электронном виде отдельным файлом в виде таблиц-закладок, подготовленным заказчиком в составе задания на расчет или при задании студенту варианта расчета в электронном виде. В этом случае локализуется источник (причина) породившая ошибку ввода исходных данных и при необходимости могут быть разработаны мероприятия исключающие вероятность ввода недостоверных данных.