Упрощенная модель генерации непрерывного кислородно-иодного лазера

Кислородно-иодный лазер (КИЛ) относится к типу лазеров с передачей энергии. Его особенностью является высокая скорость возбуждения атома йода в реакции накачки:

O 2 ( 1 А ) + 1 ( ²Р_И ) ^ O 2 ( 3 2 ) + l ( 2 P/ = ) • (1) где O 2 (- д ) . O 2 ( ³ z ) – молекула кислорода в синглетном и основном состояниях; l ( ² P^₂ ) . l ( ² P , ₂ )

– атомы йода в возбужденном и основном состояниях. Доля синглетного кислорода в потоке оп- ределяется отношением Y = O ( А )l/[O2 k

Здесь [ o 2 ( 1 А ) l - концентрация молекул кислорода в синглетном состоянии и [ O₂ 1 0 - полная

–

концентрация молекул кислорода. Для создания инверсной населенности атомов йода она долж- на превышать пороговое значение:

Y tH = ( 2K eq + 1У 1 . (2) где K _eq = k f/ k r = 0,75 х exp ( 401,4/T ) - константа равновесия процесса (1); T – температура газа. K; k f = 5,12 х 10^-12T^0,5 см³/с [1] - константа скорости прямой реакции; k r – константа скорости обратной реакции.

Эффективность КИЛ в значительной степени определяется характеристиками генератора синглетного кислорода. В химическом кислород-

но-иодном лазере (ХКИЛ) синглетный кислород нарабатывается при хлорировании щелочного раствора перекиси водорода. В большинстве используемых генераторов синглетного кислорода достигается высокая степень утилизации хлора U = G o 2 /^G_{a 2} >  ⁹⁰ %. где G O 2 и G ci 2 ^- расход кислорода на выходе из генератора и расход хлора на входе в генератор. В настоящее время генерация также продемонстрирована для элек-троразрядного кислородно-иодного лазера (ЭКИЛ), в котором синглетный кислород вырабатывается в плазмохимических процессах.

Энергетическая эффективность η непрерывного КИЛ определяется как отношение выходной мощности W out к максимально возможной извлекаемой мощности W p :

Wout Wout n W, hv Ga . (3) p Cl 2

где hν – энергия фотона, излученного на переходе i ( ²P i ₂,F = 3 ) ^ i ( ²P₃/₂,F' = 4 ) с длиной волны X = 1,315 мкм.

Большое число работ посвящено экспериментальному изучению выходных характеристик непрерывных КИЛ с химическим и электрораз-рядным генераторами синглетного кислорода [2]–[8]. В этих исследованиях использовались широкоапертурные устойчивые резонаторы, поскольку они обеспечивают наилучшие условия для эффективного извлечения энергии: однородное насыщение контура усиления, низкие дифракционные потери и т. д.

В [9]–[12] развиты простые аналитические модели, позволяющие определять выходные характеристики КИЛ с резонатором Фабри-Перо и широкоапертурными устойчивыми резонаторами. Основу этих работ составляет так называемая одночастотная двухуровневая (ОЧДУ) модель [9], [10], согласно которой кинетика заселения уровней определяется исключительно энергообменным процессом (1) и процессом индуцированного излучения на длине волны к = 1,315 мкм. Такой подход позволяет получить простые зависимости энергетических характеристик КИЛ от нескольких безразмерных критериев подобия. Но в силу существенных упрощений полученные зависимости применимы для оценок только в случаях, когда потери энергии в процессах смешения и релаксации невелики.

В настоящей работе рассматривается упрощенная аналитическая ОЧДУ модель генерации для непрерывного КИЛ с устойчивым резонатором, в которую введены безразмерные критерии подобия, имеющие ясный физический смысл. На основе сравнительного анализа расчетных и экспериментальных данных находятся области значений критериев подобия, для которых модель удовлетворительно предсказывает выходные характеристики КИЛ. Определяются значения критериев подобия, соответствующие режимам генерации с высокой энергетической эффективностью.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

Одним из важных параметров КИЛ, во многом определяющим его энергетическую эффективность, является доля 0 2 ( 1 Л ) на выходе генератора синглетного кислорода Y 0 . Соотношение (3) можно преобразовать так, чтобы значение Y 0 входило в определение энергетической эффективности. Тогда для химического КИЛ получаем выражение [12]:

П = U(Y0 - ЛYloss - Yd Kxt, = UnextmПей, , (4) где ЛYloss = ЛYdiss + ЛYrelax — Доля потеРь СИНГ— летного кислорода в резонаторе в процессах диссоциации молекул йода ΔYdiss и релаксации ΔYrelax ; Yd – доля синглетного кислорода на выхоДе резонатора; nextm = Yo - ЛYloss - Yd -эффективность извлечения энергии из активной среды; nextr = t, /(t, + а) - доля лучистой энергии, выводимая из резонатора; tr – суммарный коэффициент пропускания зеркал резонатора; α – коэффициент нерезонансных потерь (дифракционных, рассеивания и поглощения на зеркалах и т. д.). Энергетическая эффективность ЭКИЛ также может быть определена выражением (4), если множитель U принимается равным единице. Следует учитывать, что в (4) входят как изме- ряемые в экспериментах параметры U , Y0 и ηextr , так и величины ΔYloss и Yd , получаемые расчетным путем. При этом для нахождения последних достаточно рассматривать только процессы, происходящие в зоне генерации.

С целью получения некоторых общих закономерностей для описания генерации КИЛ в данной работе, как и в [9]–[12], предполагается, что кинетика активной среды полностью определяется энергообменным процессом (1). Из этого допущения следует, что ЛY , _elax = 0 . Кроме того, считаем внутрирезонаторную интенсивность постоянной во всем объеме, занятом излучением, а насыщение контура усиления – однородным, что справедливо для лазеров с широкоапертурным устойчивым резонатором [9].

Первичный газовый поток из генератора 0 2 ( 1 Л ) с долей синглетного кислорода Y 0 смешивается с вторичным потоком, состоящим из паров молекулярного йода и несущего буферного газа, перед входом в резонатор в сопловом блоке. Будем полагать, что процессы смешения и диссоциации молекулярного йода завершаются на выходе соплового блока (мгновенное смешение). Поскольку молекулы йода не диссоциируют полностью, степень диссоциации в резонаторе обычно составляет F. = 6. /(26 . ) ~ 60 - 80 %, где G _t и G _t обо- I ₂               I ₀                 I ₂                                                        I 0               2

значают расход атомарного йода на входе в резонатор и полный расход молекулярного йода соответственно. Считаем, что концентрация непродис-социировавших молекул йода в области генерации остается постоянной. Параметры потока в резонаторе (температура, статическое давление P res и скорость) предполагаются постоянными.

С этими допущениями кинетика возбуждения и процесс генерации описываются уравнениями для коэффициента усиления g , скоростей изменения концентраций 0 2 ( 1 Л ) и l ( 2 P 1/₂ ) и выражениями для полных концентраций молекул кислорода и атомов йода:

g = a([i*]-[i]/ 2),(5)

d I OdM ^] = - k f [ Ijo , ( ‘ л )] + k , [ I* ] [ O 2 ( 3 S ) ] , (6)

4* = k f [ i j o , ( ‘ Л ) ] - k , [ I* ] [ O , ( 3 S ) ] - ^h| . (7)

[0,1, =[O, (‘ Л )]+[o, (3 S )]= const,(8)

[i]o =[i*]+[i] = const,(9)

где σ – сечение вынужденного поглощения/из-лучения для доплеровски уширенного перехода i(2P^2, F = 3)^ i(2P3/2, F' = 4), определяемое выражением о = 1,3 X10 16 /Т0,5 см2; [l*], [l] — концентрации атомов йода в 2 P1 2 и 2 P3 2 состояниях соответственно; [о2 (3 х)] — концентрация молекул кислорода в основном состоянии; t = x/u - время пребывания газовой смеси в резонаторе; x – координата по потоку, отсчитываемая от начала области, занятой излучением; u – скорость потока; I – внутрирезонаторная интенсивность излучения, циркулирующего в обоих направлениях.

Выражение (5) с учетом (9) можно преобразовать так, чтобы коэффициент усиления был функцией только одной переменной – относительной концентрации возбужденных атомов йода n_It = [ l * ]/[ l ] 0 . В результате имеем

g = о[1]о (3ni* -1)/2. (10)

Так как характерное время энергообмена между синглетным кислородом и атомарным йодом намного меньше времени пребывания газовой смеси в резонаторе и [ О ₂ ] ₀ >>  [ l ] ₀ , концентрация возбужденных атомов йода может быть найдена с хорошей точностью из условия квазистационарности ( d [ l*Pdt = 0 ). Тогда из (7), учитывая (8) и (9), получаем формулу для расчета η I* как функции нормированн ~ ой внутрирезо-наторной интенсивности С = о I/(hvk f [ O₂ ] ₀ ) и доли синглетного кислорода Y :

.        (1 - Yth )(Y + C2)(1 - 3Yth )Y + 2Yth + 3C(1 - Yth ),'2

Здесь С можно охарактеризовать как параметр, определяющий отношение интенсивности установившегося поля к интенсивности накачки на верхний лазерный уровень.

Исходя из аналогичных допущений, комбинация (6) и (7) с учетом (10) и (11) позволяет получить уравнение, описывающее скорость изменения доли синглетного кислорода вдоль потока в ходе взаимодействия индуцированного излучения с активной средой:

dY = -      3C(1- Yth XY - Yth )dY    2[(1-3Yth )Y + 2Yth + 3C(1-Yth )/'2]'

где Y = 2kf [I]0t/[3(1 - Yth )] – отношение текущего времени пребывания активной среды в ре- зонаторе к характерному времени извлечения энергии синглетного кислорода (kf [l]0) 1 при бесконечно большой интенсивности внутрирезо-наторного излучения.

Нормированная внутрирезонаторная интенсивность С может быть найдена из условия стационарности генерации, которое для резонатора с однородным полем имеет вид [11]

jg(x)dx 't +|"‘d , где d – размер области, занятой излучением на зеркале, в направлении потока; L – длина усиления. Полагая скорость газа в резонаторе постоянной, в данном уравнении можно перейти к интегрированию по переменной γ и, учитывая (10), получить соотношение [12]:

Y d

3 ( 1 - Y th ) CY d

= Y i        2П      ■

где Y i = Y₀ - AY diss - начальная доля синглетного кислорода на входе в область генерации; П = 2o [l] ₀L/ ( t r + a ) - критерий подобия, выражающий отношение усиления к потерям; Y_d = 2k f [l] ₀t_d /[ 3 ( 1 - Y TH ) ] — критерий подобия, выражающий отношение времени пребывания газа в зоне генерации t_d = d/u к характерному времени извлечения энергии синглетного кислорода ( k f [l] 0 ) ¹ при бесконечно большой внутри-резонаторной интенсивности.

В ХКИЛ на диссоциацию одной молекулы йода затрачиваются три молекулы синглетного кислорода, поэтому доля потерь на диссоциацию I 2 может быть определена выражением ^AYdiss = ³ⁿi₂ F i₂ ^[12L где ⁿi₂ = G I 2/ G O 2 ^{- отно}сительная начальная концентрация I 2 в газовом потоке. Для ЭКИЛ AY diss = 0 , поскольку в диссоциации I 2 участвуют атомы кислорода.

Принимая во внимание выражения для С , γ d и П , можно установить, что второй член в правой части (13) равен эффективности извлечения энергии из активной среды

3(1 - Yth )CYd = IHd(tr + a)

2Π        2hνGO2

^ηextm ^,

где H – высота резонатора на оптической оси. Таким образом, эффективность извлечения энергии из активной среды может быть представлена ^в виде n extm = ^Yi - ^Yd .

Решение дифференциального уравнения (12) с начальным условием ^Y|_Y = ₀ = ^Yi совместно с условием стационарности генерации (13) позволяет определить долю синглетного кислорода Y d . Безразмерная интенсивность C находится с помощью итерационной процедуры. Вид этих уравнений позволяет заключить, что значение Y d и эффективность извлечения энергии из активной среды определяются значениями критериев подобия γ d и П . Энергетическая эффективность η может быть вычислена с помощью (4) при известных U и η extr .

Интегрируя (12) совместно с уравнением (13) и учитывая (14), можно получить неявную зависимость η extm как функции критериев подобия

γd и П :

(П -1 + 3Yth )п„т + [3Y„ (1 - Yth )++ -Пе„т ln| 1 - , '■ y | = 0.       (15)

Yd J V   Yi - YTH )

Из (15) непосредственно следуют уравнения для случаев протяженного резонатора ( Y d —— ^ ) и сильного поля ( П — ^ ) соответственно:

(П - 1 + 3Yth >U. +

+ [3Yth (1 - Yth )>nf 1

V

n ^

------lextrn-----

Y i - Y th )

= 0,

-

«U. = (Y-Yth

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

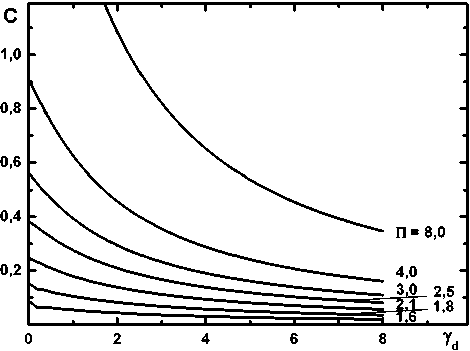
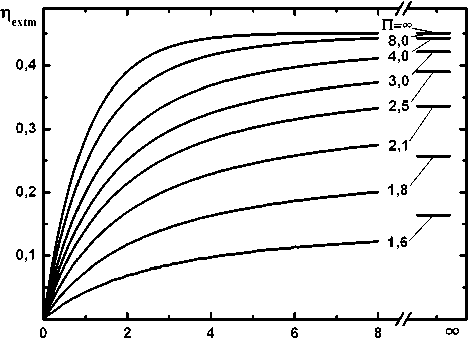
На рис. 1 показаны расчетные кривые нормированной внутрирезонаторной интенсивности (а) и эффективности извлечения энергии из активной среды (б) в зависимости от параметра Yd при Yi = 0,6 и T = 300 K для различных значений критерия, выражающего отношение усиления к потерям. Видно, что с ростом П как C , так и ηextm возрастают. В приближении резонатора бесконечной длины внутрирезонаторная интенсивность асимптотически стремится к нулю, а эффективность извлечения энергии из активной среды достигает своего максимума, определяемого уравнением (16). Решения ηextm для случая Yd —— ^ показаны горизонтальными отрезками в правой части рис. 1б. В приближении сильного поля имеем C — ^ и |extm, определяемую формулой (17), – верхняя кривая на рис. 1б. Максимальная эффективность извлечения энергии из активной среды достигается при Yd —— ^ иП —— ^ и составляет lextm = Yi - Yth . Отметим также, что YTH представляет собой долю син- глетного кислорода, соответствующую энергии недоступной для извлечения из-за наличия обратной реакции (1), а П —— ^ соответствует случаю «закрытого» резонатора (tr — 0 ).

Результаты расчетов показывают, что энергетическая эффективность может быть выше 30 % при Y d — 4 и П >  3 . Кривая эффективности извлечения энергии из активной среды для П >  8 близка к кривой, полученной для П —— ^ . Поскольку уменьшение коэффициента пропускания в выражении для П приводит также к снижению эффективности резонатора η extr , разумно ограничить значение отношения усиления к потерям П< 8 .

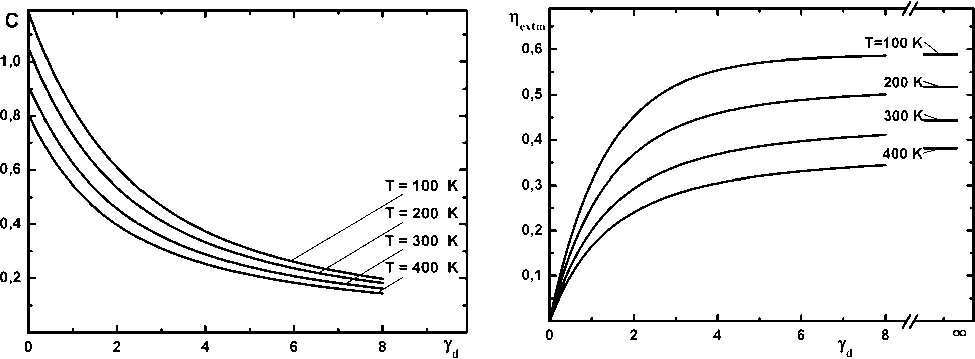
На рис. 2 приведены зависимости нормированной внутрирезонаторной интенсивности (а) и эффективности извлечения энергии из активной среды (б) для непрерывного КИЛ как функции критерия γ d для нескольких значений температуры газа T . Начальная доля синглетного кислорода и отношение усиления к потерям были приняты Y i = 0,6 и П = 4,0 соответственно. Положение горизонтальных асимптот кривых на рис. 2б в этом случае также определяется уравнением (16). Согласно упрощенной ОЧДУ модели меньшая внутрирезонаторная интенсивность и менее эффективное извлечение энергии из активной среды при более высоких температурах полностью определяются смещением влево равновесия реакции (1) с ростом T . Зависимости, представленные на рис. 2, дают возможность убедиться в преимуществах перехода в сверхзвуковой режим течения и использования предварительного охлаждения буферного газа с точки зрения получения высоких выходных характеристик.

Расчеты показывают, что эффективность извлечения энергии из активной среды максимальна в случае протяженного резонатора

Yd

а

б

Рис. 1. Изменение нормированной внутрирезонаторной интенсивности C (а) и эффективности извлечения энергии из активной среды ηextm (б) в зависимости от параметра γd при различных значениях П. Yi = 0,6 и T = 300 K

а                                               б

Рис. 2. Изменение нормированной внутрирезонаторной интенсивности C (а) и эффективности извлечения энергии из активной среды η extm (б)

значениях T . Y i = 0,6 и П = 4,0

Л , = Y— Y.” , где Y7 - доля синглетного кис-ηextm i d , d лорода при Yd —— ^. В действительности эффективность извлечения энергии из активной среды с ростом γd сначала достигает своего максимума, а затем снижается вследствие роста потерь в релаксационных процессах. Учет последних неизбежно приводит к усложнению модели, и энергетическую эффективность уже не удается представить в виде функции двух критериев подобия γd и Π . Результаты работы [2] доказывают, что существуют режимы, в которых потери энергии в релаксационных процессах незначительны, а также свидетельствуют о применимости упрощенной ОЧДУ модели для расчетов выходных характеристик непрерывного КИЛ в подобных случаях.

ОЧДУ модель, не учитывающая релаксационные потери, предсказывает, что энергетическая эффективность непрерывного КИЛ > 30 % может в зависимости от параметра γd при различных быть достигнута при уd > 4 и П = 3 — 8 . Интервалы оптимальных значений этих критериев могут быть определены более точно на основе сравнительного анализа результатов, полученных расчетным путем, и экспериментальных данных. Параметры, характеризующие режимы работы непрерывных КИЛ с высокой энергетической эффективностью [2]–[8], приведены в табл. 1. Последние две строки табл. 1 представляют параметры ЭКИЛ [8], в котором использовались два резонатора, размещенные последовательно. Предпоследняя строка содержит параметры для первого резонатора, а последняя – для второго. В этом случае доля синглетного кислорода на выходе первого резонатора является начальной для второго. В табл. 1 Gбуф – расход буферного газа. В экспериментах в качестве буферного газа использовался азот, либо его смесь с гелием.

Таблица 1. Параметры, характеризующие режим работы КИЛ в экспериментах, в которых достигнута высокая химическая эффективность

G Cl 2 (ммоль/c)	G I 2 (ммоль/c)	G буф (ммоль/c)	[I] 0 (см-3)	T (K)	P res (Торр)	u (см/c)	L (см)	d (см)	H (см)	W out
										(Вт)	Работа
17.4	0.44	28.0	7.5×1014	2801)	2.31)	4,3×104	5.0	3.61)	1.61)	627	[2]
20.0	0.25	63.8	4.1×1014	268	3.02)	3,1×104	7.5	5.02)	2.02)	599	[3]
470.0	11.0	1410.0	7.0×1014	220	1.8	6,5×104	37.0	6.0	6.0	13500	[4]
23.1	0.09	0.0	0.4×1014	3503)	0.25	0,7×104	100.03)	7.0	3.0	630	[5]
22.0	0.35	10.0	6.1×1014	360	1.3	3,2×104	10.0	4.5	1.4	581	[6]
33.0	0.9	210.0	13.8×1014	2204)	7.1	4,7×104	5.0	4.5	2.0	770	[7]
135.0	1.3	1530.9	2.7×1014	124	3.0	7,5×104	22.9	4.25)	2.55)	392.6	[8]
135.0	1.3	1530.9	2.7×1014	124	3.0	6,3×104	22.9	4.25)	3.05)	88.4

¹⁾ Б.Д. Бармашенко (частное сообщение), ²⁾ M. Эндо (частное сообщение), ³⁾ Н.Н. Юрышев (частное сообщение), ⁴⁾ М.В. Загидуллин (частное сообщение), ⁵⁾ Д.Л. Кэрролл (частное сообщение)

Важной характеристикой, фигурирующей в выбранной модели и оказывающей большое влияние на результаты экспериментов и расчетов, является концентрация атомов йода. Если известен коэффициент усиления, ее можно с высокой точностью определить по формуле

[ I i o = g • σ

( 1 - 3Y th ) Y . + 2Y th

Y - Y 0 TH

Таким образом определялась концентрация атомарного йода в условиях работ [2]–[4] и [8]. Для [5]—[7] значение [ l i . рассчитывалось в предположении известной степени диссоциации с учетом приведенных данных о соотношении расходов молекулярного йода и кислорода.

На основе параметров, приведенных в табл. 1, определены критерии подобия γd и Π , а также расчетные значения энергетической эффективности ηcal (табл. 2). Наблюдается хорошее согласие между расчетными и измеренными значениями энергетической эффективности, разница An = ncal — nexp — 3 %, за исключением [7]. Мож- но сделать вывод, что рекордная химическая эффективность в [2] достигнута в основном за счет высокого отношения усиления к потерям П = 7,7. Однако даже при П > 10 энергетическая эффективность ЭКИЛ [8] далека от предельно достижимой, поскольку Yd < 1. Анализ данных, представленных в таб. 2, показывает, что для работ, в которых сообщается об энергетической эффективности nexp ^ 30 %, безразмерные критерии подобия находятся в интервалах Yd = 3 — 6 и П = 3 — 8. Обобщая расчетные и экспериментальные результаты, можно заключить, что эффективное извлечение энергии из активной среды непрерывного КИЛ достигается при Yd = 4 — 6 и П = 3 — 8. В качестве правой границы интервала для первого критерия выбрано значение, близкое к тому, которое реализовано в [6], где ηexp ~30 %.

Кинетические потери [2]–[7] определяются потерями на диссоциацию и составляют 1–6 % в случае ХКИЛ и равны нулю для ЭКИЛ [8] (табл. 3). Кроме того, некоторая доля молекул

	Таблица 2. Параметры, определяющие энергетическую эффективность КИЛ
U	η cal       η exp        Δη γ d           П          C       η extm       t r          α        η extr                                  Работа (%)     (%)     (%)
0.94	4.1          7.7         0.7       0.47    0.007 1)     0.0006 1) 0.92 40.6 39.6 1.0       [2]
0.90	4.2         2.7         0.2       0.42 0.016 0.0018 0.90 33.7 32.9 0.8       [3]
0.95	3.6          4.1          0.3       0.38 0.1        0.01       0.91 32.6 31.5 1.1        [4]
0.99 2)	3.3          5.2         0.4       0.33 0.01      0.001 2)       0.91 30.1 30.0 0.1        [5]
0.92	6.7         5.8         0.2       0.35 0.013 0.0013 0.91 29.1 29.0 0.1       [6]
0.93	7.4          3.0         0.1       0.40 0.037 0.0037 3) 0.91 33.5 25.6 7.9       [7]
1.00	0.6         11.8        0.6       0.04 0.01205  0.00002 4)     1.00 4.1 3.2 0.9
1.00	0.7         13.9         0.4       0.03 0.01025   0.00002 4)     1.00 2.8 0.7 2.1         [8]

¹⁾ Б.Д. Бармашенко (частное сообщение), ²⁾ Н.Н. Юрышев (частное сообщение), ³⁾ М.В. Загидуллин (частное сообщение), ⁴⁾ Д.Л. Кэрролл (частное сообщение).

Таблица 3. Параметры, характеризующие преобразования энергии, запасенной в синглетном кислороде

Y 0	η I 2	F I 2	ΔY diss	Y i	Y d	Y TH	ΔY out	-у ~ Y d	ΔY loss	χ	Работа
0.68	0.027	0.50	0.04	0.64	0.17	0.14	0.03	0.14	0.04	0.86	[2]
0.70	0.014	0.63	0.03	0.67	0.26	0.13	0.13	0.15	0.03	0.73	[3]
0.60	0.025	0.76	0.05	0.55	0.17	0.10	0.07	0.10	0.06	0.75	[4]
0.60 1)	0.004	0.80	0.01	0.59	0.26	0.18	0.08	0.18	0.01	0.79	[5]
0.60	0.017	0.80	0.04	0.56	0.21	0.18	0.03	0.18	0.04	0.83	[6]
0.60 2)	0.029	0.60	0.05	0.55	0.15	0.10	0.05	0.10	0.05	0.79	[7]
0.13 3)	0.010	0.73	0.00	0.13	0.09	0.03	0.06	0.03	0.00	0.39	[8]
0.09	0.010	0.73	0.00	0.09	0.06	0.03	0.03	0.03	0.00	0.44

¹⁾ Н.Н. Юрышев (частное сообщение), ²⁾ М.В. Загидуллин (частное сообщение), ³⁾ Д.Л. Кэрролл (частное сообщение).

синглетного кислорода AY out = Y d — Y TH выносится из резонатора. Эти потери «на вынос» могут быть высокими при Y d <  4 и П <  3 . Так, в [3] отношение усиления к потерям низкое П = 2,7 , и AY out = 0,13 . Эти потери также высоки (7–8 %) в [4] и [5], где критерий подобия у d <  4 не достигает оптимального значения. Однако, природа указанных потерь в [3] и [4], [5] различна. В первом случае активная среда характеризуется низким коэффициентом усиления, а во втором – малая длина резонатора вдоль потока не позволяет обеспечить эффективное извлечение энергии из активной среды. Из таб. 3 можно видеть, что значения ΔY out минимальны для [2] и [6], где Y d >  4 и Π >  3 . В [7] энергетическая эффективность значительно отличается от расчетной ( An = 7,9 %), что при Y d = 7,4 и П = 3,0 можно объяснить потерями на релаксацию, не учитываемыми в выбранной модели.

Энергетическая эффективность η является неподходящим параметром для сравнения выходных характеристик ХКИЛ и ЭКИЛ, поскольку имеется значительное различие между долями О₂ ( 1 A ) на выходе химического и электроразряд-ного генераторов синглетного кислорода. Для этой цели наиболее удобным параметром является отношение доступной энергии к максимальной доступной энергии [9], определяемое как

X =

Y 0

—

ΔY loss

—

Y d

Y 0

—

Y

TH

ηextm

Y - Y

0 TH

Как видно из таб. 3, этот параметр для ХКИЛ найден равным X = ^{0,73 — 0,86} . В настоящее время для ЭКИЛ χ ~ 0,4 , что сравнительно далеко от оптимального значения. В последнем случае извлечение мощности ограничено скоростью передачи энергии от кислорода к йоду, и около половины наработанных молекул синглетного кислорода выносится из резонатора.

ВЫВОДЫ

Упрощенная ОЧДУ модель, предложенная для описания генерации непрерывного КИЛ [9]– [12], позволяет ввести два безразмерных критерия подобия, γ d и Π , имеющих ясный физический смысл, в которые входят измеряемые в экспериментах параметры. Критерий γ d выражает соотношение времени пребывания газового потока в зоне генерации и времени извлечения энергии синглетного кислорода, а критерий П определяет, во сколько раз усиление излучения в активной среде превышает порог оптических потерь резонатора.

ОЧДУ модель может быть использована для оценок выходных параметров непрерывного

КИЛ с устойчивым резонатором, если потери энергии в релаксационных процессах незначительны, для Y d — 6 . Анализ расчетных и экспериментальных результатов показывает, что эффективное извлечение энергии из активной среды непрерывного КИЛ достигается при Y_d = 4 — 6 и П = 3 — 8 . При меньших Y d и П значительная часть энергии выносится из резонатора с газовым потоком, а при больших значениях этих параметров существенными становятся релаксационные потери в активной среде и оптические потери.

Работа выполнена при поддержке госконтрак-та № 16.740.11.0494 в рамках федеральной целевой программы “Научные и научно-педагогические кадры инновационной России”.