Упрощенное моделирование теплового режима металлооксидного варистора в области токов утечки

Ограничители перенапряжения (ОПН) на основе МОВ широко используются в электрических сетях 35–220 кВ для предотвращения негативного воздействия импульсных явлений на изоляцию электротехничего оборудования [1–3]. ОПН должны эффективно ограничивать импульсные перенапряжения, при этом гарантированно не достигая режима тепловой неустойчивости. Опасность теплового пробоя может возникать как при воздействии мощного импульса перенапряжения, так и в установившемся режиме работы сети [4, 5] из-за отрицательного температурного коэффициента МОВ [6]. Большинство существующих моделей процессов в МОВ направлены на получение оптимальных условий работы без избыточных затрат на материалы.

Построение математической модели МОВ существенно различается в зависимости от режима работы МОВ. Во время действия короткого импульса перенапряжения в МОВ может происходить разделение (шнурование) проводящих каналов, что учитывается в мультифизических моделях [6–9]. Также существует много моделей, учитывающих локальную неоднородность структуры МОВ. Данные модели позволяют оптимизировать размеры зерна оксида цинка и как результат – технологию производства МОВ.

Целью моделирования МОВ и ОПН при токах утечки является определение условий достижения тепловой неустойчивости. Прямое построение таких моделей сталкивается как с большим объемом расчетов из-за существенного различия времени установления теплового режима и периода приложенного напряжения, так и плохой сходимостью моделей из-за большой нелинейности токов проводимости. Указанные сложности увеличиваются, когда рассматривается полная конструкция ОПН [10, 11]. В [12] был предложен расчет теплового режима путем разделения образца на слои и установления взаимосвязей между слоями. Недостатком такого способа является сложность программной реализации и дискретность модели. В [13, 14] предложен и реализован вариант усреднения теплового воздействия по периоду приложенного напряжения, но при моделировании не была учтена зависимость проводимости от температуры. Последнее может приводить к значительным ошибкам в расчетах, поскольку в [4] сообщается, что проводимость может существенно изменяться в пределах рабочего диапазона температур.

Целью настоящего исследования является оптимизация тепловой модели ОПН в диапазоне токов утечки, а также экспериментальная верификация методики построения моделей с учетом температурной зависимости проводимости МОВ.

Математическая модель

Электрическая модель МОВ основывается на системе уравнений Максвелла в квазистационар-ном приближении [4], дополненной материальными уравнениями. Относительная диэлектрическая проницаемость принимается равной ε = 800 согласно [4], а проводимость материала является функцией двух параметров: Е – мгновенное значение напряженности электрического поля; Т – мгновенное значение температуры в точке. Таким образом, мгновенную проводимость можно записать в виде a = a(E,T). (1)

В [4] показано, что оптимальный вариант аппроксимации для функции (1) имеет вид

• / v \ A ⁺ B ( T - T >) I I

o ( E , T ) = O 0 +| — I , (2) I ^E о )

где σ 0 , E 0 , T 0 – базовые значения проводимости, напряженности поля и температуры; А , В – параметры, учитывающие температурную зависимость.

Тепловая модель ОПН основывается на стандартном уравнении теплопередачи [15, 16], дополненной распределенным источником тепла:

Q = Q ( e , t ) , (3) выделяющегося при протекании тока в МОВ в данный момент времени.

В результате получается связанная мультифи-зическая задача, в которой напряженность поля вычисляется по электрической модели [17], а температура – из уравнения теплопередачи [16]. При этом проводимость (1) в электрической модели является функцией температуры, а источник тепла (3) зависит от напряженности электрического поля. Сильная нелинейность задачи при зависимостях (2) приводит к большим затратам вычислительных ресурсов, а в некоторых случаях – к проблемам со сходимостью модели. Также следует отметить, что характерное время изменения приложенного к МОВ напряжения намного меньше, чем время достижения установившегося теплового режима МОВ.

Для оптимизации модели предлагается провести усреднение по периоду приложенного синусоидального напряжения. Для электрической части модели можно считать, что температура в течение периода внешнего напряжения не изменяется, и получить эквивалентные зависимости проводимости материала от действующих значений напряженности поля Е _д при различных температурах Т:

^ = ^' ( E д , T ) .                                  (4)

Критерием эквивалентности будет выделившаяся за период тепловая энергия:

Q = c' ( E д , T ) E 2 V .                         (5)

В (5) учтено, что электрическое и тепловое поле внутри МОВ фактически однородно, а температура Т выступает в качестве параметра, поскольку изменение температуры в течение периода несущественно.

В тепловой части модели источники тепла также будут зависеть от действующих значений напряженности поля Е _д:

Q = Q ( E д , T ) ,                              (6)

что позволит существенно сократить время моделирования.

Соотношение между проводимостью для мгновенных значений (1) и проводимостью для действующих значений (3) можно определить при помощи поправочного температурного коэффициента:

2 j sin ( w t ) A ⁺ B ^{( T 20 )} sin ( w t ) ² dt

F ( T ) = -0------------------------

где τ = 0,01 с – половина периода приложенного напряжения.

Имитационное моделирования

Для получения значения проводимости (4) и выделившейся теплоты (6) при температуре Т = 20 °C было проведено численное моделирование протекания тока через МОВ высотой h _МОВ = 22 мм и радиусом r _МОВ = 21 мм, подробно исследованный в работе [18].

На рис. 1 показано синусоидальное напряжение с действующим значением U = 3,5 кВ, приложенное к МОВ, и зависимости токов через МОВ при разных действующих значениях напряжения. Граничные условия при моделировании исключали энергообмен с окружающим пространством, вещество считалось однородным и изотропным. Зависимости на рис. 1 качественно согласуются с приводимыми в литературе экспериментальными кривыми [4, 19, 20].

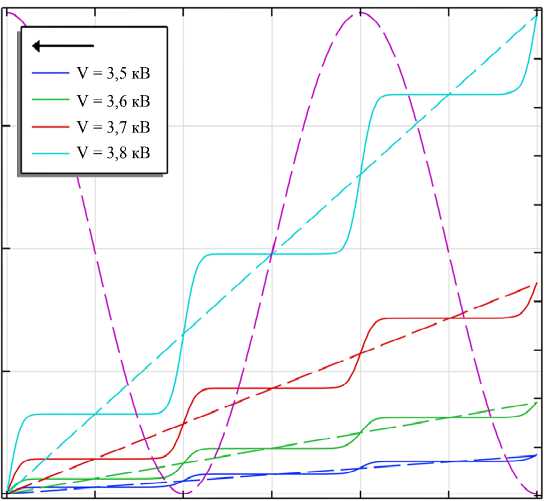
Моделирование теплового режима в течение 30 мс было проведено в мультифизической модели. Результаты изменения температуры приведены на рис. 2 сплошными линиями для нескольких действующих значений приложенного напряжения. Согласно (5) был получен эквивалентный режим и для него также показаны изменения температуры (пунктирные линии). Для удобства анализа графиков на рис. 2 также показаны зависимости приложенного напряжения.

Данные на рис. 2 подтверждают эквивалентность теплового режима, установленного при помощи (5) и, следовательно, возможность применения соотношений (4) и (6) для дельнейшего моделирования.

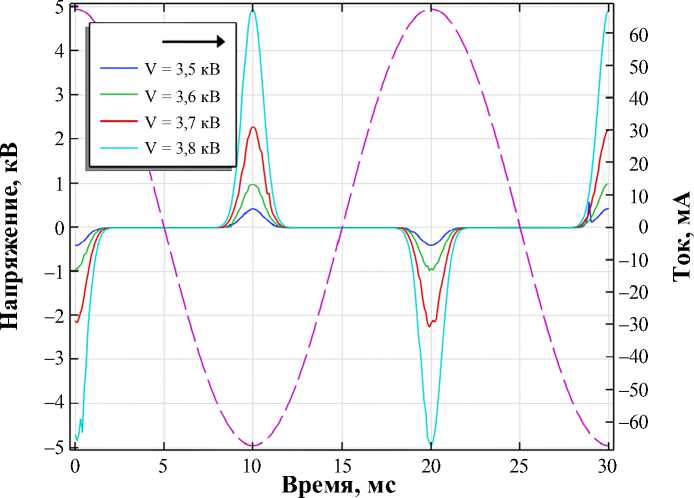
Рис. 1. Токи утечки МОВ при различных напряжениях МОВ Fig. 1. MOV of leakage currents at different voltages

293,18

я

>> 293,17

я а

=

S щ Н

293,16

293,15

V = 3,5 кВ

V = 3,6 кВ

V = 3,7 кВ

V = 3,8 кВ

0         5        10        15        20        25        30

–1

–2

–3

–4

–5

аГ

Время, мс

Рис. 2. Согласование моделей по эквивалентной выделенной энергии Fig. 2. Matching models by equivalent radiated energy

Верификация модели

Характеристики типа (2) можно найти в литературе [4], однако зависимости сильно различаются для разных образцов даже при одинаковой температуре [18]. Поэтому для верификации модели были получены оригинальные экспериментальные данные.

В эксперименте МОВ нагревался до температуры Т = 130 °C, к нему прикладывалось напряжение, которое образец может выдержать в длительном режиме, и нагреватель выключался. При остывании образца проводились измерения напряжения, тока и температуры образца. Измерительная схема была стандартная [19], реализованная в составе установки LH-2/6. Напряжение измерялось трансформатором напряжения HJ12-15 (15 кВ/150 В)

и вольтметром Tektronix DMM 4020 5-1/2, измерение тока осуществлялось при помощи шунта сопротивлением 1 кОм, температура измерялась термосопротивлением Pt100.

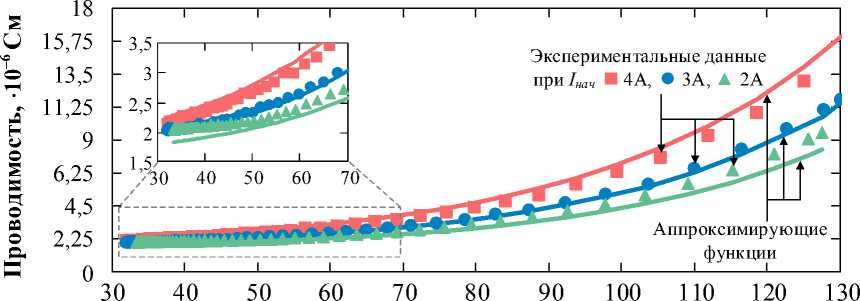
Графики экспериментальных зависимостей проводимости от температуры и аппроксимирующие функции при различных начальных значениях тока показаны на рис. 3. Аппроксимация экспериментальных данных была выполнена по формуле (2) для всех опытов одновременно. В результате методом наименьших квадратов были получены параметры: σ₀ = 1,50·10^–6 См/м, Е ₀ = 3,78·10⁵ В/м, А = 20,67, В = –0,0445 1/К.

Анализ рис. 3 показывает, что была получена достаточно хорошая сходимость результатов. Не-

Температура, °C

Рис. 3. Зависимости проводимости от температуры Fig. 3. Dependences of MOV conductivity on temperature

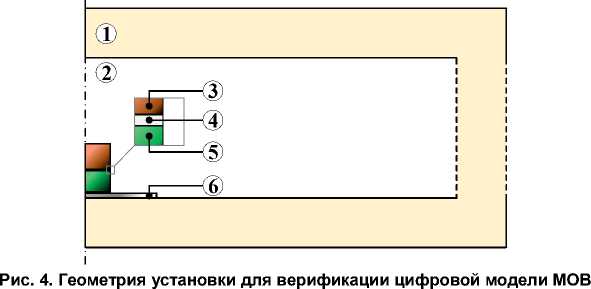
Fig. 4. Geometry of the setup for verification of the digital MOV model

которое отличие расчетных и экспериментальных данных могло возникнуть из-за погрешностей, вносимых металлизированными гранями МОВ [21], а также из-за того, что при обработке данных эксперимента не учитывались внутренние сопротивления приборов.

Используя параметры в (2), полученные при аппроксимации экспериментальных данных, были восстановлены эквивалентные зависимости (4) и (6). Зависимость (6) была использована как характеристика материала МОВ в тепловой модели.

Экспериментальное исследование и моделирование было выполнено для геометрии экспериментальной установки, показанной на рис. 4 без учета масштаба. Установка обладает осевой симметрией. Использованные обозначения и размеры: 1 – теплоизоляция стенок печи из экструдированного пенополистирола толщиной d сп = 40 мм.; 2 – воздух в печи; 3 – медный цилиндр ( r м = 20 мм, h м = 25 мм); 4 – металлизированная грань МОВ ( r _а = 21 мм, h _а = 0,25 мм); 5 – МОВ; 6 – стальная подложка ( r _с = 67 мм, h _с = 4 мм).

К МОВ было приложено напряжение 3,5 кВ, благодаря чему образец стал нагреваться из-за токов утечки. Температура в точке между МОВ и стальной подложкой контролировалась при помощи датчика температуры.

При моделировании процесса в контактных областях 3–4–5–6–1 основным механизмом передачи тепла принята теплопроводность и процесс описывался при помощи стандартных уравнений [15]. Тепловые свойства материалов приняты согласно [9], зависимости для МОВ были получены ранее в (4) и (6). Основным механизмом передачи тепла в воздухе считался конвективный теплообмен, тем самым данная область описывалась уравнениями Навье – Стокса [16]. Параметры воздуха приняты согласно библиотеке материалов COMSOL Multiphysics.

Температурные зависимости, полученные при экспериментальном исследовании и имитационном моделировании, показаны на рис. 5. Наличие экстремума температуры после 12 часов эксперимента можно объяснить тем, что стенки печи про-

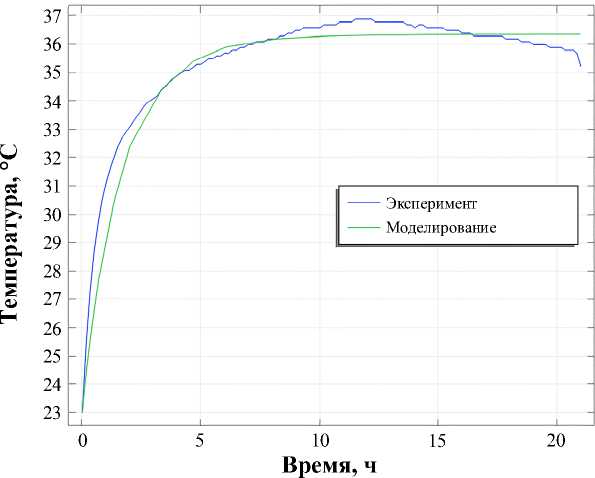
Рис. 5. Сравнение результатов моделирования с экспериментальными данными Fig. 5. Comparison of simulation results with experimental data

грелись и начался отток тепла от внешних поверхностей стенок. Сравнение результатов имитационного моделирования и эксперимента показывает хорошую сходимость, и это позволяет утверждать, что описанная методика расчетов верифицирована.

Обсуждение

Использование в тепловой модели характеристик для действующих значений позволяет существенно сократить время моделирования тепловых режимов во всех элементах конструкции ОПН на основе МОВ во всем диапазоне токов утечки. Указанная экономия достигается за счет того, что временной решатель подбирает шаг по времени, исходя из скорости установления тепловых режимов в материалах, а не из скорости изменения приложенного напряжения. Также неоспоримым преимуществом перехода к тепловой модели для действующих значений является существенное уменьшение степени нелинейности тепловой модели по сравнению с мультифизической моделью процесса. Численные опыты показывают, что экономия времени наблюдается в 20–100 раз.

Исходя из построения и верификации модели, можно сделать вывод, что рассмотренная методика ограничивается только областью токов утечки. Во-первых, полученная аппроксимация для материальных уравнений справедлива только в области токов утечки и может существенно измениться в области больших и средних токов. Во-вторых, в области больших и средних токов время тепловых процессов сравнимо со временем импульса и в усреднении по внешнему воздействию нет необходимости.

Применять описанную методику можно как для оценки теплового режима ОПН при устано- вившемся режиме сети, так и для анализа переходного теплового процесса после мощных импульсных воздействий. Поскольку при моделировании используются материальные уравнения вещества в МОВ, то каких-либо ограничений на геометрию ОПН не наблюдается. Таким образом, описанная методика может применяться для расчета ОПН любого класса напряжения.

Примененная методика усреднения по периоду внешнего электрического поля может быть применена и для других материалов с существенно нелинейными свойствами зависимости проводимости от электрического поля и температуры. Для установления зависимостей типа (4) и (6) нужно проводить аналогичные эксперименты и расчеты. Рассмотренный алгоритм позволяет сформулировать границы применимости данного метода усреднения – в течение периода приложенного напряжения изменение температуры образца должно быть намного меньше его температуры.

Заключение

Предложена математическая модель теплового режима МОВ с эквивалентными характеристиками для действующих значений. В модели учтена температурная зависимость проводимости МОВ.

Модель верифицирована путем сравнения экспериментально наблюдаемого теплового режима МОВ с результатами упрощенного теплового расчета.

Рассмотренная модель позволит существенно упростить анализ теплового режима ОПН на основе МОВ в области токов утечки, а также других электротехнических устройств с нелинейными материалами в квазистационарных по изменению температуры режимах.