Упрощенный метод Дункерли для оценки первой частоты колебаний регулярной фермы

1 Введение / Introduction

На практике для расчета собственных частот колебаний стержневых конструкций применяют метод конечных элементов [1]. Численно-аналитический метод расчета колебаний регулярных структур применен в [2]. В [3] разработана новая эквивалентная динамическая модель для анализа связанных вибраций фермы космической антенны. Эксперименты на вибрацию большой развертываемой в космосе антенны с кольцевой ферменной конструкцией с предварительным анализом уменьшенной ее копией выполнены в [4]. Найдены собственные частоты и соответствующие формы колебаний. Для изучения механизма разрушения стальных арочных ферм, в условиях сильных землетрясений, в [5] была проведена серия испытаний на вибростенде. С помощью метода конечных элементов в работе оценено влияние форм крепления на разрушение конструкции и воздействие повреждений на напряженно-деформированное состояние системы. Результаты сравниваются с экспериментом.

В некоторых случаях при упрощении модели конструкции возможны и аналитические решения в виде оценки первой частоты снизу по методу парциальных частот Донкерлея или сверху по энергетическому методу Рэлея [6]. В статье Воробьева О.В. [7] в аналитической форме найдены обе эти оценки для плоской фермы. В [8] обсуждается использование метода Донкерлея для оценки собственных частот башенных конструкций, включая и асимметричную геометрию фермы. В качестве практического примера рассмотрен анализ колебаний асимметричной высоковольтной опоры ЛЭП. В [9] для расчета собственных частот используется метод Донкерлея в итеративной постановке. В работе [10] показано, что формула Донкерлея дает нижнюю границу основной частоты колебаний упругой системы, которую можно разделить на ряд отдельных компонентов с различной гибкостью. Использование полученной формулы иллюстрируется рассмотрением однородной консоли и трехслойной балки. Новое выражение для нижней границы основной собственной частоты конструкции приводится в [11] и исследуется его связь с формулой Донкерлея. Получена улучшенная оценка основной частоты, которая применяется для приближенного выражения основной частоты системы грунт -конструкция, включающей структуру с одной степенью свободы, плоское жесткое основание и упругий грунт. Полученное приближение сравнивается с известными решениями.

Наибольший практический интерес представляют решения для регулярных ферм, содержащие порядок фермы (число периодических структур) в качестве параметра. Регулярными статически определимыми фермами занимались Hutchinson R.G. и Fleck N.A. [12], [13]. Большой вклад в теорию регулярных ферм и их классификацию внес Kaveh A. [14]. Объектом исследования [15] является пространственно-консольная статически определимая ферма, состоящая из трех плоских ферм с поперечной решетчатой системой, соединенных по длинным сторонам. В аналитическом виде методом Донкерлея находится зависимость первой собственной частоты колебаний фермы от количества панелей, размеров, веса, конструкции и свойств материала. В [16] исследуется статически определимая ферма с двумя пролетами и ромбовидной решеткой. Зависимость первой собственной частоты колебаний фермы от ее размеров, массы, а также количества панелей находится в аналитическом виде. Жесткость конструкции с массами, сосредоточенными в ее узлах, определяется по формуле Максвелла-Мора. Нижняя аналитическая оценка первой частоты вычисляется по формуле Донкерлея. Обобщение ряда частных решений для ферм с последовательно увеличивающимся числом панелей выполнено методом индукции.

Другой аналитический подход к анализу строительных конструкций — метод начальных функций. Формула зависимости первой частоты плоской фермы Финка от числа панелей выведена в [17]. В [18] представлены два подхода к построению приближенных аналитических решений изгиба прямоугольной тонкой пластины: метод суперпозиции, основанный на методе начальных функций, и метод, построенный с использованием функции Грина, в виде ортогонального ряда. Этот же метод с использованием системы компьютерной математики Maple применен и в [19]. Расчет ферм в нелинейной постановке выполнен в [20], [21]. Сравнительный анализ некоторых точных решений задачи о прогибе плоских регулярных ферм, полученных в системе Maple, выполнен в [22]. В [23] приведено аналитическое решение для первой частоты собственных колебаний пространственной конструкции по методу Донкерлея.

• 2    Материалы и методы / Materials and Methods

2.1    Конструкция фермы

Предлагаемый метод применяется к плоской регулярной ферме балочного типа с нисходящими раскосами (рис. 1). Ферма симметричная, число панелей равно 2 n .

Рис. 1 – Схема фермы, n =4

Fig. 1 – The truss scheme, n =4

Высота фермы h, длина пролета 2 na . Вся конструкция состоит из N = 8 n + 4 стержней, включая три стержня, моделирующие опоры. Число шарниров, наделенных массами m, равно K = 4 n + 2. Таким образом, число степеней свободы этой системы равно K . Для расчета усилий в стержнях, которые потребуются для формулы Максвелла – Мора при расчете жесткости конструкции, необходимо пронумеровать узлы и стержни (рис. 1), и ввести в программу [24] координаты узлов. Начало координат выбрано в левой подвижной опоре:

X = x + 2 n + 1 = a ^{( i} - !)» y i = ⁰, y + 2 n + 1 = ^h,¹ = U^{2 n +} !.

Порядок соединения стержней задается специальными списками концов стержней. Нижний пояс, например, кодируется следующими списками: Ф _i = [ i , i' + 1], i = 1,..,2 n.

2.2    Численный расчет частот колебаний фермы

В узлах фермы располагаются одинаковые массы m, совершающие вертикальные колебательные движения. Динамические уравнения системы записываются в матричной форме:

mI K Y + D K Y = 0.                                  (1)

Здесь Y — вектор вертикальных смещений масс в узлах фермы, Y — вектор ускорений, I_K — единичная матрица, D_K — матрица жесткости. Матрица податливости B_K является матрицей, обратной к матрице жесткости D_K , и вычисляется по формуле Максвелла – Мора:

N

Ь^= Ё S? Sl а /( EF ).                               (2)

а= 1

Введены стандартные обозначения: b ij — перемещение узла i от действия единичной вертикальной безразмерной силы, приложенной к узлу j, 8*01 ' ) — усилия в стержне а от действия единичной вертикальной силы, приложенной к узлу i , где расположена масса m , l _а -длина стержня с номером а , EF — продольная жесткость одинаковая для всех стержней.

Для гармонических колебаний с частотой ю очевидна связь Y = —ю ² Y . Умножением уравнения (1) слева на матрицу B_K , задача сводится к проблеме собственных значений матрицы B_K : B K Y = X Y , где Х = 1/( ю ² m ) — собственное число матрицы B K , ю — собственная частота колебаний. Собственная частота колебаний выражается через собственные числа матрицы B K : ю 1 / ( m X ) .

Аналитическое решение для фермы с произвольным числом панелей в общем случае получить невозможно. Методом Донкерлея можно оценить первую частоту снизу, методом Рэлея — сверху.

2.3    Оценка первой частоты по Донкерлею

Нижняя приближенная оценка для первой частоты по методу Донкерлея имеет вид [8]:

K

• —2

юD = Ё юp ,

Р = 1

где ю _p — парциальные частоты. Для нахождения парциальных частот составляются уравнения движения отдельных масс:

тур + Dpyp = 0, p = 1,2,..., K.

Коэффициент жесткости D_p, обратный к коэффициенту податливости, вычисляется по формуле Максвелла – Мора в предположении, что жесткости всех стержней одинаковы:

.,2

8p = 1/Dp = Ё(8(p') lj/(EF) = Up/(hEF)■ j=1

Из (3) и (4) при Y p = A p sin( to t + ф ) следует выражение для парциальной частоты to p = D p / т . Отсюда:

KK toD = т Ё 5p = т Ё up /(h2EF) = mUn /(h2EF).                   (6)

p = 1         p = 1

K

Здесь введено обозначение: U n = £ u p . Расчет серии ферм с разным числом панелей

p = 1

дает следующую последовательность сумм в (6):

U 1 = a ³ + c ³ + 9 h ³, U 2 = (26 a ³ + 10 c ³ + 33 h ³)/2,

U3 = (553a3 +105c3 + 241 h3)/9, U4 = 3(252a3 + 28c3 + 53h3)/4, где c = a а2 + h2. В общем случае

U = Ca ³ ₊ Cc ³ ₊ Ch 3 . n 1   23

Для определения трех коэффициентов в (8) последовательность (7) требуется продлить по крайней мере до 10 элементов, и получить общие члены последовательностей как решение рекуррентных уравнений в системе Maple:

C 1 = (4 n ² - 1)(8 n ² + 7) / 45, C ₂ = (4 n ² - 1) / 3, C ₃ = (4 n ³ + 11 n ² + 11 n + 1) / (3 n ). (9)

Оператор rgf_findrecur системы Maple, возвращающий рекуррентное уравнение для членов последовательности, требует последовательность четной длины. Выражения (9) получаются как решения этих уравнений с помощью оператора rsolve. Таким образом, оценка по Донкерлею первой частоты колебаний рассматриваемой фермы имеет вид:

ш

D

= h

EF m (C1a3 + C2c3 + C3h3)'

2.4 Упрощенный вариант расчета первой частоты

Формула (10) с коэффициентами (9) сравнительно компактна, однако она получена для простейшей фермы. Для более сложных регулярных конструкций коэффициентов в ней может быть больше, а сами выражения для них значительно сложнее. Связано это с тем, что K вычисление коэффициентов содержит суммирование Un = ^ up , что в аналитической форме p=1

бывает или сложно, или даже невозможно. Упростить преобразования можно, вычислив сумму по среднему значению ее слагаемого. На рисунке 2 показана зависимость u_p от номера узла, в котором расположена масса при a =2м , h =3м . Сумма U_n ординат в значениях p =1,2,.., K на рисунке 2 пропорциональна площади, ограниченной кривой графика.

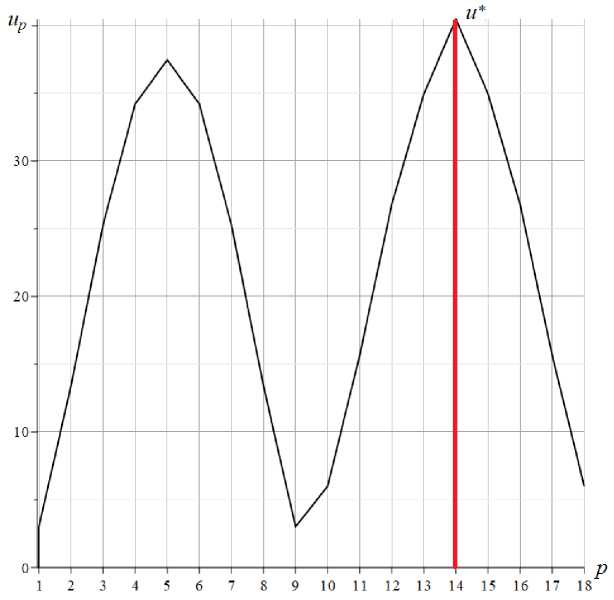
Рис. 2 – Зависимость коэффициента u_p от номера узла фермы при n =4

Fig. 2 – The dependence of the coefficient u_p on the number of the truss node for n =4

Если перестроить этот график, расположив коэффициенты u_p , соответствующие парциальным частотам, по возрастанию (рис. 3), то площадь фигуры, ограниченной кривой (та же сумма ординат) не изменится. При этом сумму U_n можно вычислить как площадь трапеции:

K

U n = Z u p = K ( u 1 + u *)/2, p = 1

где u 1 , u * — минимальное и максимальное значения коэффициента u p (рис. 3).

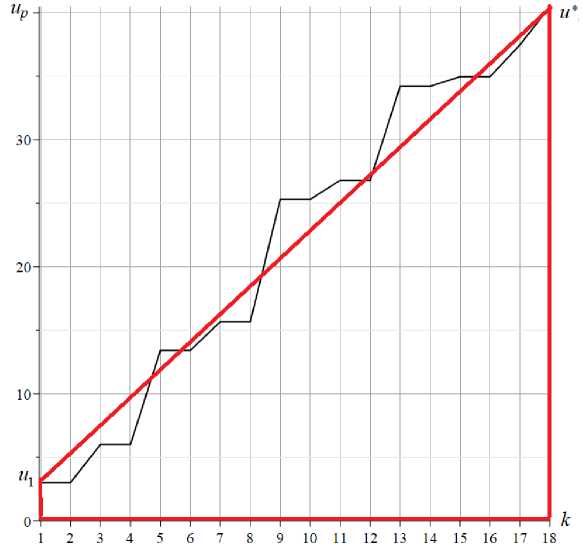
Рис. 3 – Коэффициенты u_p в порядке возрастания при n =4

Fig. 3 – Coefficients u_p in ascending order at n =4

Трапеция представляет собой вписано-описанную фигуру по отношению к реальной фигуре, площадь которой вычисляется. Поэтому есть уверенность, что предлагаемая оценка будет близка к оценке Донкерлея.

Вычисление (10) при n =1,2,... дает следующую последовательность более простую для анализа, чем (7):

U 1 = ( a ³ + c ³ + 9 h ³)/2, U ₂ = (6 a ³ + 2 c ³ + 7 h ³)/2,

U 3 = (19 a ³ + 3 c ³ + 8 h ³)/2, U 4 = (44 a ³ + 4 c ³ + 9 h ³)/2,...

Коэффициенты в (8) находятся обобщением этой последовательности и имеют вид:

C 1 = n (2 n ² + 1)/6, C ₂ = n /2, C 3 = ( n + 5)/2.                         (11)

Последовательности коэффициентов при таком подходе получаются сравнительно простыми и не требуют применение системы Maple. В более сложных задачах для обобщения последовательностей можно применять операторы rsolve и rgf_findrecur или аналогичные операторы системы Mathematica [6], [25].

Таким образом, предлагаемое упрощенное решение по Донкерлею имеет вид:

ш

D '

= h

6EF m (n (2n2 + 1)a3 + 3nc3 + 3(n + 5)h3)

• 3    Результаты и их обсуждение / Results and Discussion

Для сравнения методов аналитических оценок можно использовать решение, полученное численно для всего спектра частот собственных колебаний фермы. Принята длина панели фермы: a = 2м, высота h = 4м. Площадь поперечных сечений стержней решетки и опорных стержней принимается одинаковой: F = 9 см² . Массы в узлах m = 600кг , модуль упругости материала стержней E = 2,1 - 10⁵ MПa (сталь). На рисунке 4 представлены зависимость от числа панелей частоты ю D по стандартной формуле Донкерлея (10) с коэффициентами (9), частоты ш _в , по упрощенной формуле Донкерлея (12) и найденная численно значение первой частоты ю 1 спектра системы с K степенями свободы.

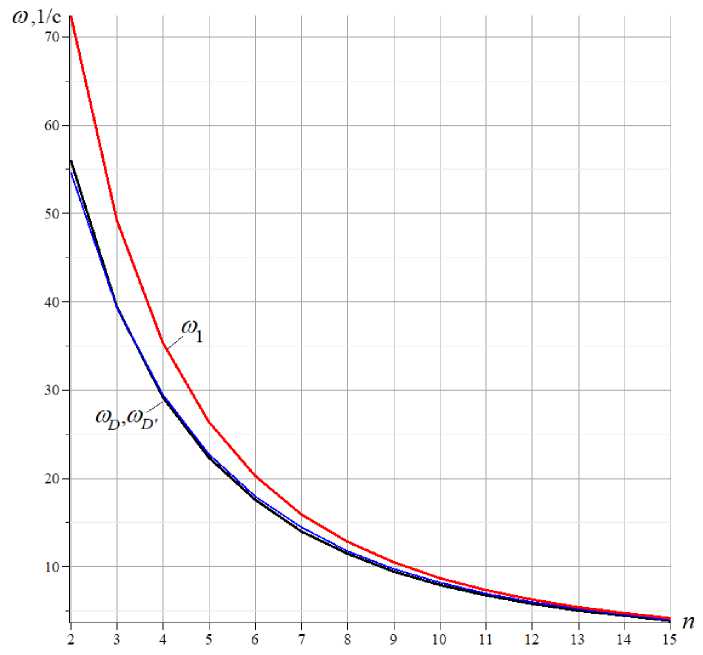
Рис. 4 – Зависимость от числа панелей первой частоты колебаний по трем методам

Fig. 4 – Dependence on the number of panels of the first oscillation frequency by three methods

Метод Донкерлея и его упрощенный вариант дают почти одинаковые значения (кривые практически сливаются). При этом на всем диапазоне значений числа панелей, как и ожидалось, оценки Донкерлея меньше первой частоты спектра, полученного численно с учетом всех степеней свободы. Как меняется погрешность приближенных решений при изменении числа панелей видно из рисунка 5. Вводятся величины относительных погрешностей: s D = | го D -Ю 1 |/ го 1 и s D , = | го D , -го 1 |/ го 1 . С увеличением порядка фермы погрешность предлагаемого упрощенного метода падает быстрее, чем погрешность метода Донкерлея, и достигает приемлемой величины в несколько процентов при n >12 .

Если при n =2 погрешность метода Донкерлея несколько меньше погрешности предлагаемого метода, то при n = 15 ситуация обратная. Точность упрощенного метода Донкерлея в несколько раз выше. Метод лучше всего подходит для оценки в аналитической форме первой частоты колебаний ферм с большим количеством панелей.

Предлагаемый метод предназначен для вывода аналитического решения для регулярных систем произвольного порядка. При фиксированном порядке рассчитываемой конструкции трудностей суммирования коэффициентов U_n не возникает, и для приближенного расчета первой частоты в символьной форме можно напрямую использовать метод Донкерлея или даже метод Рэлея, который дает значительно более высокую точность. Нет смысла также использовать упрощенный метод Донкерлея и в случае численного расчета первой частоты с применением специализированных пакетов. Современные численные пакеты легко справляются с задачей расчета спектра частот систем с многими степенями свободы.

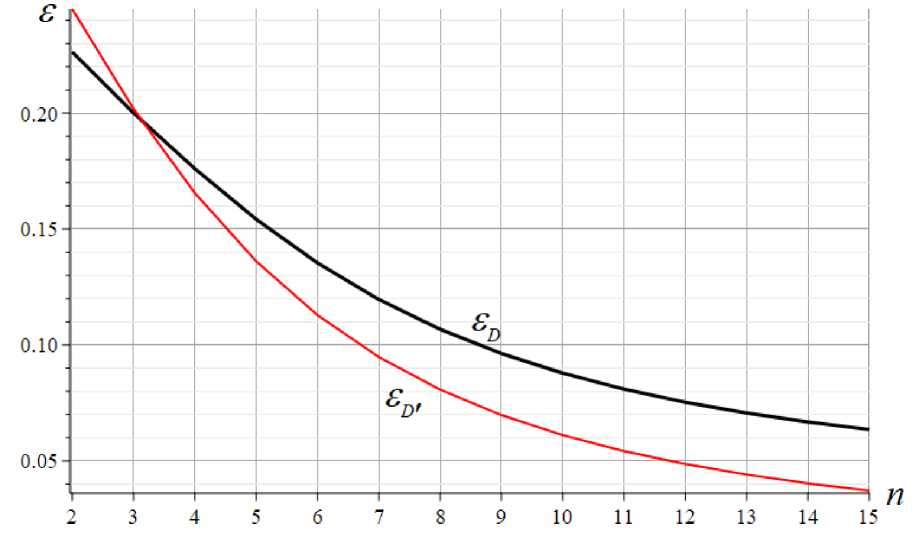
Рис. 5 – Сравнительная погрешность методов

Fig. 5 – Comparative error of methods

Предлагаемый метод может быть использован для вывода формулы нижней границы первой частоты в зависимости от порядка регулярности, например, применительно к оценке численного решения, полученного для конструкции (не обязательно фермы) с весьма большим числом степеней свободы. Именно в этом случае численные методы начинают давать ошибки, обусловленные как неизбежным накоплением погрешностей округления ("проклятие размерности"), так и просто за счет ошибок моделирования сложной конструкции. Погрешность же предлагаемого метода с увеличением порядка регулярности только уменьшается.

• 4    Выводы/ Conclusions

Основные результаты работы:

• 1.    Предложен метод нахождения первой частоты колебаний регулярной механической системы с многими степенями свободы. Метод позволяет в компактной аналитической форме оценить эту частоту снизу.

• 2.    На примере решения задачи о колебании простой балочной фермы показано, что погрешность предлагаемого метода меньше, чем погрешность метода Донкерлея и уменьшается с увеличением числа панелей.

• 5    Fundings

  Работа выполнена при финансовой поддержке РНФ 22-21-00473.