Упрощенный расчет момента инерции поперечного сечения консоли под нагрузкой
Автор: Дерюгин Е.Е.
Журнал: Advanced Engineering Research (Rostov-on-Don) @vestnik-donstu
Рубрика: Механика
Статья в выпуске: 2 т.24, 2024 года.
Бесплатный доступ
Введение. Опубликованные исследования жесткости консолей под нагрузкой фокусируются на вопросах их деформации и разрушения. Описаны расчеты момента инерции - принципиально важной характеристики прочности стержня. Однако не решена проблема значительных затрат времени для таких вычислений. Представленное исследование восполняет данный пробел. Цель работы - описание нового быстрого метода аналитического расчета распределения напряжения сдвига в сечении консоли, соответствующего действию внешней приложенной силы. Впервые в таком контексте рассматриваются касательные напряжения и приводятся примеры расчета момента инерции для двух нестандартных сечений консоли.Материалы и методы. Для создания нового метода консоль представили как пачку пластинок, ориентированных параллельно вектору внешней силы. Исходные расчеты строили по схеме консольной балки с выделенной пластинкой. Деформацию стержневых элементов моделировали с учетом действия однородного поля напряжения сдвига в сечении пластинки. Для обоснования упрощенного расчета момента инерции сечений задействовали схемы квадрата, эллипса, треугольника, шестиугольника, шестиконечной звезды и фигурного креста. Использовали аналитические и математические методы исследования, в частности теорему Гюйгенса-Штейнера.Результаты исследования. Создан быстрый универсальный метод вычислений момента инерции поперечного сечения консоли под нагрузкой. Его отличие - отказ от расчетов для каждого сечения с учетом формы и других особенностей. При любой форме сечения балка представляется как пачка бесконечно тонких пластинок, моменты их инерции интегрируются, и используется известное решение для прогиба тонкой пластинки. Метод позволяет однозначно показать распределение касательных напряжений на торце консоли, обеспечивающих заданный прогиб, причем впервые для таких решений используются касательные напряжения. Получены их профили в зависимости от направления внешней приложенной силы. Впервые выведены формулы для моментов инерции сложных сечений - шестиконечной звезды и фигурного креста. Каждое сечение соотнесено с кривой распределения напряжения и его максимальным значением. Эти данные визуализированы в виде диаграмм. Установлено, что момент инерции и жесткость консоли не меняются при повороте внешней приложенной силы на 30° для сечения в виде звезды и на 45° - для квадрата и фигурного креста. В общем случае поле касательных зависит от геометрической формы и от ориентации сечения относительно внешней приложенной силы.Обсуждение и заключение. Предложенный упрощенный подход к расчету момента инерции поперечных сечений консолей дает возможность однозначно определить поле касательных напряжений на торце, обеспечивающее при заданном прогибе соответствующее значение внешней приложенной силы. Инженеры и механики могут использовать результаты представленной работы при расчетах и моделировании деформации стержневых элементов конструкций.
Деформация стержня, момент инерции плоской фигуры, момент инерции сложных сечений, упругий прогиб консоли, распределение касательных напряжений
Короткий адрес: https://sciup.org/142241587
IDR: 142241587 | УДК: 624, | DOI: 10.23947/2687-1653-2024-24-2-159-169
Текст научной статьи Упрощенный расчет момента инерции поперечного сечения консоли под нагрузкой
Финансирование. Работа выполнена в рамках государственного задания Министерства науки и высшего образования Российской Федерации (тема № FWRW–2021–0009. № ЕГИСУ НИОКТР 121031100276–2).
Original Theoretical Research
Simplified Calculation of the Inertia Moment of the Cross Section of the Console under Loading
Evgeny E. Deryugin
Institute of Strength Physics and Materials Science, Siberian Branch of Russian Academy of Sciences, Tomsk, Russian Federation
Introduction. Published studies on the rigidity of consoles under load focus on the issues of their deformation and destruction. Calculations of the inertia moment, fundamentally important characteristic of the strength of the rod, are described. However, the problem of significant time consumption for such calculations has not been solved. The presented study meets the lack. The objective of the work is to describe a new rapid method for analytical calculation of the shear stress distribution in the section of the console corresponding to the action of an external applied force. For the first time, tangential stresses are considered, and examples of calculating the inertia moment for two non-standard sections of the console are given in this context.
Materials and Methods. To develop a new method, the console was presented as a pack of plates oriented parallel to the vector of external force. The source calculations were based on the scheme of a console beam with a dedicated plate. The deformation of the rod elements was modeled taking into account the effect of a uniform shear stress field in the plate section. To validate the simplified calculation of the inertia moment of the sections, schemes of a square, ellipse, triangle, hexagon, six-pointed star, and a figured cross were used. Analytical and mathematical research methods were applied, specifically, the Huygens–Steiner theorem.
Results. A rapid valid method for calculating the inertia moment of the cross section of the console under loading has been developed. Its difference is the rejection of calculations for each section, taking into account the shape and other features. For any shape of the section, the beam is represented as a bundle of infinitely thin plates, their inertia moments are integrated, and a well-known solution for deflection of a thin plate is used. The method allows us to unambiguously show the distribution of tangential stresses at the end of the console, providing a given deflection, and tangential stresses are used for such solutions for the first time. Their profiles are obtained depending on the direction of the external applied force. Formulas for the inertia moments of complex sections — a six-pointed star and a figured cross — are derived for the first time. Each section is correlated with the stress distribution curve and its maximum value. This data is visualized in the form of diagrams. It is found that the inertia moment and the rigidity of the console do not change when the external applied force is rotated by 30° for a star-shaped section and by 45° for a square and a figured cross. In general, the tangent field depends on the geometry and on the orientation of the section relative to the external applied force.
Discussion and Conclusion. The proposed simplified approach to calculating the inertia moment of the cross sections of the consoles makes it possible to uniquely determine the field of tangential stresses at the end, which provides the appropriate value of the external applied force for the given deflection. Engineers and mechanics can use the results of the presented work in the calculations and modeling of deformation of rod structural elements.
Acknowledgements. The author would like to thank the Editorial team of the Journal and anonymous reviewers for their competent expertise and valuable recommendations for improving the quality of the article.
Funding Information. The research is done within the frame of the government task of the Ministry of Science and Higher Education of the Russian Federation (topic no. FWRW–2021–0009. USISU R&D No. 121031100276–2).
Введение. Многие строительные конструкции содержат элементы в виде стержней, которые в процессе изготовления или эксплуатации испытывают упругие деформации [1] . Прочность стержня или балки на изгиб определяет несущую способность конструкции [2] . Способность балки к упругой деформации характеризуется жесткостью, определяемой как отношение нагрузки P к упругому прогибу балки λ e : m x = P / λ e [3] . Как правило, в лабораторных условиях жесткость проверяют на консольной балке. Один ее конец заделывают в жесткое основание, а на другой действует внешняя сила, направленная перпендикулярно оси балки [4] . Моделирование и расчеты характеристик деформации и разрушения стержней, как правило, связаны с решением задачи о прогибе консольной балки, или консоли, под действием внешней приложенной силы [5] . При этом нет публикаций о простых и универсальных методах определения моментов инерции сложных сечений относительно действия внешней приложенной силы. Решение этой задачи описано в представленной статье.
Цель данной работы — создание универсального, быстрого метода расчета моментов инерции сложных сечений консоли под действием внешней приложенной силы. Новый подход позволяет аналитически узнавать распределение напряжения сдвига в сечении, соответствующее действию внешней приложенной силы. Отметим, что ранее в таких вычислениях не принимались во внимание касательные напряжения. Кроме того, впервые приводятся примеры расчета момента инерции для сложных фигурных сечений.
Материалы и методы. Во многих работах по сопротивлению материалов, например в [6] , приводится универсальная формула для расчета упругого прогиба консоли, λ e . Согласно этой формуле, жесткость консоли равна:
Pl X e = 3 EIx/L\ (1)
где E — модуль Юнга; L — длина консоли; I x — момент инерции поперечного сечения балки относительно оси x , проходящей через центр тяжести сечения перпендикулярно приложенной силе P .
Из уравнения (1) следует, что принципиально важной характеристикой консоли является момент инерции сечения I x , величина которого зависит от геометрической формы поперечного сечения балки и направления оси x [7] . Следует подчеркнуть, что в уравнении (1) момент инерции I x относится к оси x , которая перпендикулярна направлению внешней приложенной силы P . В частности, момент инерции прямоугольного сечения a × b относительно оси симметрии x равен [8] :
Ix — ab 3/12. (2)
Здесь a — толщина консоли; b — ее ширина. Сила P направлена параллельно стороне b прямоугольника.
Подставляя (2) в (1), получим известное уравнение для прогиба консоли прямоугольной формы [9] :
i _ 4 P { L \
X .
Ea I b )
Поперечные сечения консольных балок, или консолей, бывают разными. На рис. 1 приведен простой пример консоли квадратного сечения под действием внешней силы P , направленной вдоль диагонали квадрата.
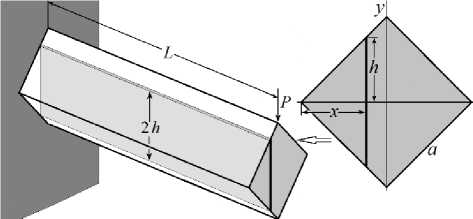
Рис. 1. Схема консольной балки с выделенной пластинкой
Моментом инерции сечения относительно оси x называется сумма, или интеграл, произведений элементарных площадок ds = dxdy на квадраты расстояний y площадок до оси x : Ix — JJ y 2 dxdy . [10] . Подынтегральная функция, в сущности, является моментом инерции элементарной площадки dxdy относительно оси x .
Консоль можно представить в виде пачки предельно тонких пластинок толщиной dx и длиной L , ориентированных параллельно вектору силы P . Под действием P все пластинки прогибаются на одну и ту же величину λ e . При заданной ориентации сечения консоли отдельная пластинка не испытывает влияния деформации остального объема. Тогда момент инерции сечения консоли в целом будет определяться интегральной суммой моментов инерции сечений всех пластинок в пачке.
Проекция пластинки на плоскость поперечного сечения консоли представляет собой прямоугольную полоску толщиной dx и полудлиной h (рис. 1). Момент инерции сечения отдельной пластинки можно рассматривать как
Механика
момент инерции консоли прямоугольного сечения 2 h × dx . По определению, к каждой пластинке в пачке применимо уравнение типа (2), где a = dx и b = 2 h . Согласно этому выражению, момент инерции полоски равен dI x = 2 h 3( x ) dx / 3. Таким образом, момент инерции сечения консоли можно определить интегрированием моментов инерции не элементарных площадок, а элементарных полосок:
I c = 3 J B h (x )3 dx , (3)
где x изменяется в пределах от A до B .
Условие ориентации плоскости пластин параллельно вектору внешней приложенной силы важно, поскольку позволяет однозначно связать упругий прогиб консоли λ e с распределением касательных напряжений в поперечном сечении консоли. Все пластинки в пачке прогибаются на одну и ту же величину λ e . Согласно (1), dI x = 2 h 3( x ) dx / 3. Значит, для пластинки толщиной dx потребуется элементарная сила dP = 3 l e EdI x / L 3 = 2 l e Eh 3( x ) dx / L 3. Такая сила соответствует действию однородного поля напряжения сдвига в сечении пластинки ds ( x ) = 2 h ( x ) dx :
T = dP / ds = X e Eh 2 ( x )/ L 3 (4)
Из (4) видно, что значение напряжения τ в системе координат xy не зависит от координаты y .
Уравнение (4) удобно использовать при моделировании деформации стержневых элементов конструкции.
Интеграл (3) определяет момент инерции сечения I c относительно оси x , проходящей через центр тяжести сечения. В случае несимметричных и сложных сечений удобно сначала найти момент инерции сечения или части сечения относительно оси, которая не проходит через центр тяжести сечения. Затем нужно перейти к моменту инерции сечения I c относительно оси, которая проходит через центр тяжести сечения. Известно, что момент инерции сечения повторяет свойства момента инерции твердого тела и подчиняется теореме Гюйгенса–Штейнера [11] . Момент инерции сечения I x относительно произвольной оси x равен сумме момента инерции этого сечения I с относительно оси, проходящей через центр тяжести сечения параллельно оси x , и произведения площади сечения S на квадрат расстояния a между осями: I x = I с + a 2 S . Поэтому в общем случае можно записать:
Ix = 2 J B h ( x )3 dx + a 2 s = I c + a 2 s . (5)
Если ось x проходит через центр тяжести сечения, то расстояние a = 0 и уравнение (5) переходит в (3).
Результаты исследования. Для создания простого, быстрого и универсального метода вычислений откажемся от расчетов для каждого сечения с учетом его формы и других особенностей. Именно такой подход впервые реализован в рамках данной научной работы. Каким бы сложным ни было сечение, достаточно использовать известное решение для прогиба тонкой пластинки, представить балку в виде пачки бесконечно тонких пластинок и проинтегрировать их моменты инерции. Кроме того, метод позволяет однозначно показать распределение касательных напряжений на торце консоли, обеспечивающих заданный прогиб. Подчеркнем, что касательные напряжения в таком контексте рассматриваются впервые.
Упрощенный расчет момента инерции простых сечений. Для обоснования предлагаемого метода рассмотрим известные сечения простой геометрической формы. Далее вместо выражения «момент инерции поперечного сечения консоли» используем термин «момент инерции». Будем считать, что внешняя приложенная сила всегда направлена перпендикулярно оси x , относительно которой определяется момент инерции сечения.
Квадрат. Уравнение (2) получено при условии, что вектор силы, приложенной к торцу консоли, перпендикулярен стороне a прямоугольника. При b = a получим момент инерции квадратного сечения I c = a 4/12.
Найдем предлагаемым методом момент инерции квадрата относительно оси x , которая параллельна не стороне, а диагонали квадрата (рис. 2 a ).
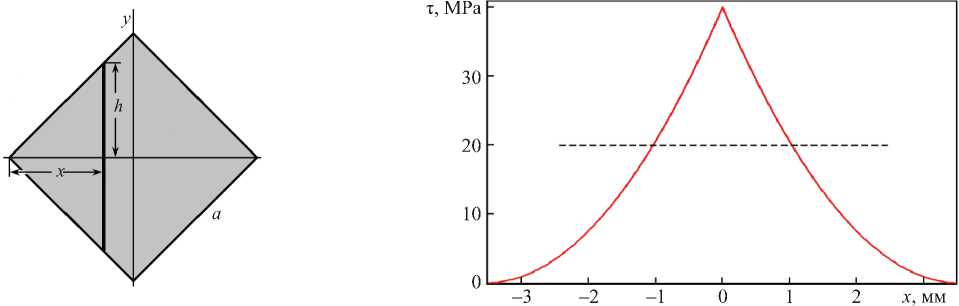
а) б)
Рис. 2. Схема сечения в виде квадрата: а — сечение, б — распределение напряжения τ вдоль оси x
Полудлина полоски на рис. 1 равна h = x . Из уравнения (3) находим:
2 a/ 3
3 J - a/ V3
I c
a 4
x3 dx = — .
Видно, что поворот оси x на 45° не меняет момент инерции квадратного сечения. Следовательно, при повороте внешней приложенной силы на 45° не меняется и жесткость консоли (1).
Подставляя x в вместо h (4), получим распределение напряжения сдвига в сечении консоли квадратного сечения, соответствующее прогибу λ e :
t ( x ) = X ex 2 E / L 3.
На рис. 2 б представлено распределение т ( x ) вдоль диагонали квадрата при К = 2 мм и a = 5 мм. Согласно (1), действие напряжения сдвига т ( x ) на торце консоли из стали ( E = 200 MPa) длиной L = 50 мм соответствует действию внешней приложенной силы P = 0,25 E λ e a 4/ L 3 = 500 N . Максимальное напряжение τ max = 40 MPa наблюдается на вертикальной диагонали квадрата. При отклонении от диагонали резко до нуля уменьшается напряжение τ. В результате в системе т ( x ) образуется острый пик.
Напряжение τ зависит только от переменной x , поэтому по графику на рис. 2 б можно определить значение τ в любой точке квадрата.
Очевидно, что при ориентации силы перпендикулярно сторонам квадрата τ = P / a 2 = 20 MPa (рис. 2 б , пунктирная линия). Как видно, распределение напряжения т ( x ) в сечении, соответствующее внешней силе P , существенно зависит от ее направления.
Эллипс. На рис. 3 a приведена схема эллипса с полуосями a и b . Начало координат — в центре эллипса.
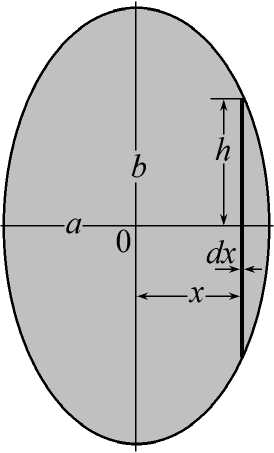
а)
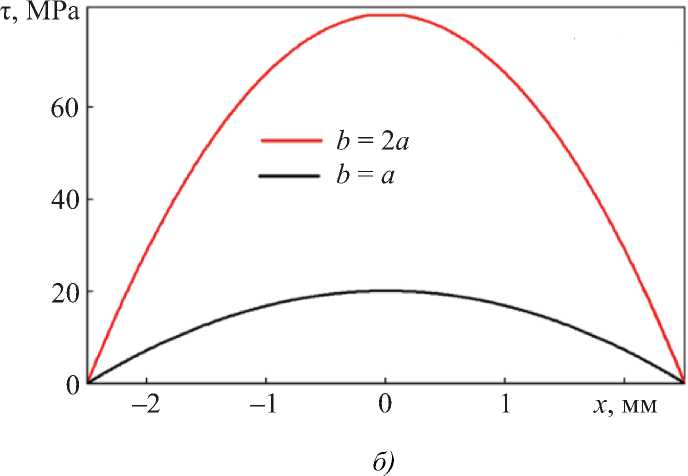
Рис. 3. Схема сечения в виде эллипса с полуосями a и b:
а — эллипс; б — распределения τ вдоль полуоси a. 1 — a = b , 2 — b = 2 a , a = 2,5 мм
Из канонического уравнения эллипса [12] следует, что полоска, выделенная на рис. 3, имеет полудлину h = b ( a 2 – x 2)1/2 / a . Подставляя эту величину в (3) и интегрируя от – a до + a , получим момент инерции эллиптического сечения:
. 2 a3 2 b 3 a 3 /2 п ab 3
Ic = h dx = I a - x I dx = . (6)
c 3 - a 3 a 3 - a L J 4
При a = b = r выведем момент инерции кругового сечения: π r 4 / 4, где r — радиус окружности.
Подставляя в (4) значение h , соответствующее эллипсу, получим следующее распределение напряжения сдвига в сечении консоли эллиптической формы:
t ( x ) = X eb 2(1 — x 2 / a 2) E / L 3.
На рис. 3 б представлено распределение τ( x ) вдоль полуоси a = 2,5 мм при λ e = 2 мм, E = 200 MPa и L = 50 мм. При сравнении его с распределением τ( x ) на рис. 2 б для квадрата очевидно существенное влияние геометрической формы сечения консоли на распределение напряжений. В случае эллиптического сечения на кривой τ( x ) отсутствует острый пик. Максимальное напряжение τ max наблюдается вдоль полуоси b . С учетом требования λ e = const можно говорить о быстром росте напряжения τ max при увеличении отношения b / a . При увеличении полуоси b в два раза τ max увеличивается в 4 раза (рис. 3 б ).
Механика
Треугольник. Рассмотрим сечение в виде равнобедренного треугольника (рис. 4). Ось x направлена вдоль высоты треугольника (рис. 4 a ). На расстоянии x от основания треугольника полудлина полоски равна h = b ( a – x ) / 2 a .
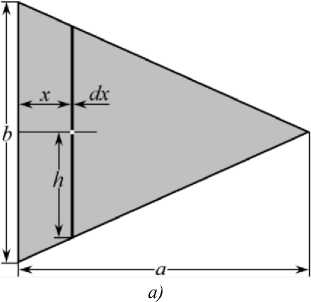
Рис. 4. Схема сечения в виде равнобедренного треугольника: a — ось x , сила направлена параллельно основанию; б — сила направлена перпендикулярно основанию
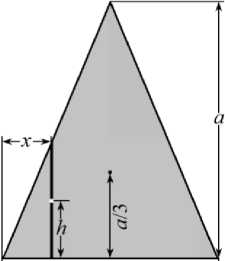
■b- б)
Интегрирование выражения (4) по x от 0 до a определит следующую величину момента инерции:
I с
b 3 a b 3 a
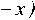
= (a dx =--- .
12 a 3 0 48
Рассмотрим случай, когда ось x проходит через центр тяжести и параллельна основанию треугольника (рис. 4 б ).
Полоска на расстоянии x от левого угла треугольника имеет полудлину h = xу/ 4 a 2 / b 2 -1 / 2 (рис. 4 б . Центр тяжести полоски расположен на расстоянии h от основания треугольника (рис. 4 б ). Следовательно, согласно теореме Гюйгенса–Штейнера для поперечного сечения, момент инерции полоски относительно основания треугольника равен:
dIc = —h 3 dx + 2 h 3 dx = —a— x 3 dx.
c 33 b 3
Интегрирование полученного выражения по переменной x от – b /2 до b /2 определит момент инерции треугольника относительно основания:
Ix = a3 b/12. (8)
Центр тяжести треугольника расположен на расстоянии a /3 от основания. Согласно теореме Гюйгенса–Штейнера [13] , момент инерции треугольника относительно собственного центра тяжести будет меньше (8) на величину:
Г =f a I S = ab,
1 3 J 18
где S = ab /2 — площадь треугольника.
Следовательно, момент инерции треугольника относительно собственного центра тяжести равен:
I c
a 3 b a 3 b a 3 b
72" - 78" = 76.
Полученный результат в точности соответствует табличному значению момента инерции сечения относительно оси через центр тяжести, параллельной основанию треугольника.
На рис. 5 приведены распределения напряжения сдвига в треугольном сечении при λ e = 2 мм для случаев, когда сила прогиба направлена вдоль основания ( а ) и вдоль высоты треугольника ( б ).
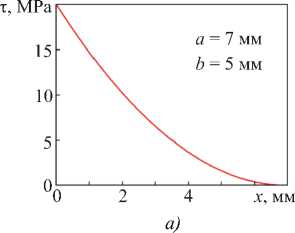
Рис. 5. Распределения τ в треугольном сечении: а — сила направлена вдоль основания; б — сила направлена вдоль высоты треугольника
При ориентации треугольника как на рис. 4 a напряжение τ( x ) плавно уменьшается от τ max на основании до 0 на вершине (рис. 5 а ). При ориентации треугольника как на рис. 4 б распределение τ( x ) (рис. 5 б ) подобно распределению для квадратного сечения, когда сила ориентирована вдоль диагонали (рис. 2 б ).
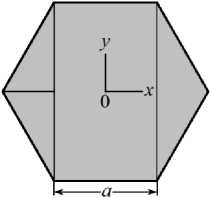
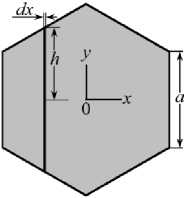
Правильный шестиугольник. На рис. 6 представлены две ориентации шестиугольника относительно оси x : параллельно ( а ) и перпендикулярно ( б ) его диагонали.
а)
б)
Рис. 6. Правильный шестиугольник:
а — диагональ перпендикулярна вектору силы; б — диагональ параллельна вектору силы
Сечение шестиугольника на рис. 6 а состоит из:
-
- прямоугольника шириной а и высотой a 13;
-
- двух равнобедренных треугольников высотой а /2 и с основанием а ^3.
Найдем моменты инерции указанных частей сечения по (2) для прямоугольника и по (7) для треугольников. Для прямоугольника в уравнении (2) b = a √3, поэтому его момент инерции равен I x 1 = √3 a 4/4. Для треугольных частей в уравнении (7) основание равно b = a √3, а высота a /2. Следовательно, момент инерции шестиугольника:
Ix = IxI +1x 2 = A 3 a 4 (114 +1/16) = 5 A 3 a 4/16.(10)
Если приложенная сила направлена вдоль диагонали шестиугольника (рис. 6 б ), то полудлина полоски равна a /2 – x /√3. Совершив соответствующие замены в (4), получим:
2 a3/2
Ic = (a-x/V3) dx = ——.
3 - a V3 / 2
Сравнивая (10) и (11), убеждаемся, что поворот шестиугольника на 30° не влияет на его момент инерции относительно оси x .
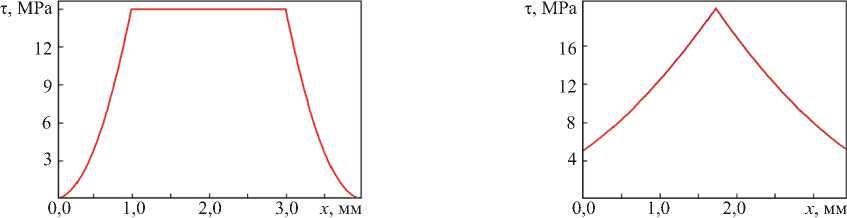
Рассмотрим случай ориентации шестиугольника как на рис. 6 a . При λ = 2 мм и Е = 200 MPa в интервале от – a /2 до + a /2 напряжение τ( x ) будет постоянным и равно τ max = 15 MPa (рис. 7 а ). При тех же условиях и ориентации шестиугольника как на рис. 6 б распределение τ ( x ) подобно распределению для квадратного сечения (рис. 2 б ). Однако здесь τ max = 20 MPa и τ min = 5 MPa (рис. 7 б ).
а) б)
Рис. 7. Распределение τ (x) в сечении правильного шестиугольника: а — диагональ перпендикулярна вектору силы; б — диагональ параллельна вектору силы
Примеры упрощенного расчета момента инерции сложных сечений
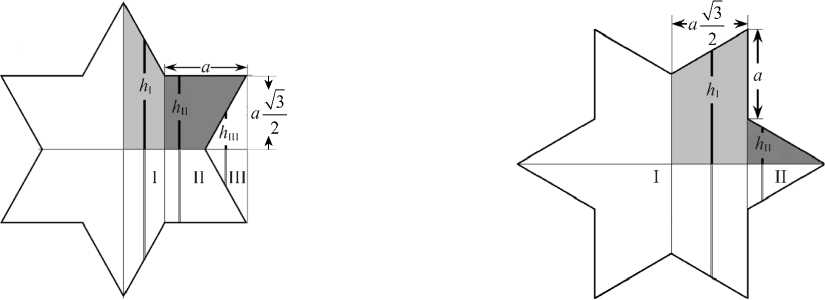
Шестиконечная звезда. Рассчитаем предлагаемым методом момент инерции нестандартного сечения в виде правильной 6-конечной звезды со стороной a . Для определения момента инерции относительно малой диагонали звезды воспользуемся схемой на рис. 8 а . Выделим на схеме три зоны: зону I шириной a /2, зону II для остальной части полфигуры и примыкающую к ней вспомогательную зону III в виде треугольника.
Механика
а) б)
Рис. 8. К расчету момента инерции шестиконечной звезды относительно: а — малой диагонали; б — большой диагонали
Полудлина полоски в зоне I на расстоянии x от диагонали равна h I = √3( a – x ). Используя выражение (3), для двух зон I на рис. 6 a получим момент инерции:
15 - Л
a 4 .
a/ 2 3
IxI = 2V3 (a - x) dx = a/2
Момент инерции зоны II равен моменту инерции прямоугольника высотой a √3 и шириной a без момента инерции треугольника III. Полудлина полоски в прямоугольнике равна h II = a √3/2. Из уравнения (3) находим момент инерции прямоугольника:
I ii+ш = 4 a .
Полудлина полоски в треугольнике равна h III = x √3. Согласно (4), момент инерции треугольника равен:
I i = —a .
III 32
Следовательно, момент инерции зоны II равен:
I II
= I II+Ш
- 1
III 32 a
Удвоенная сумма моментов инерции зон I и II определит момент инерции 6-конечной звезды:
T 11-Л
1 x I = —a 4 . (12)
Для определения момента инерции звезды относительно большой диагонали следует воспользоваться схемой на рис. 8 б , где выделены две зоны. Полудлина полоски в зоне I равна h I = a + x/ √3, в зоне II h II = a /2 – x/ √3. Из (3) вычисляются моменты инерции зон I ( I x I = a 465√3/96) и II ( I x II = a 4√3/96). Можно убедиться, что удвоенная сумма моментов инерции зон I и II в точности соответствует уравнению (12). Следовательно, момент инерции 6-конечной звезды относительно большой и малой диагоналей одинаков.
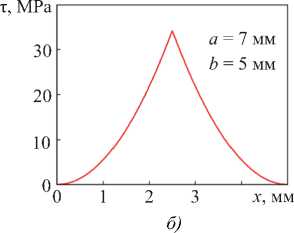
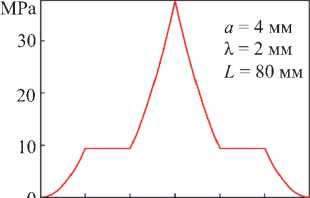
На рис. 9 а показано распределение напряжения сдвига в сечении 6-угольной звезды, соответствующее λ = 2 мм и ориентации внешней приложенной силы согласно рис. 8 а . Вдоль вертикальной оси звезды напряжение принимает максимальное значение τ max = 37,5 MPa. По мере удаления от оси вправо τ быстро падает до уровня τ = 9,375 MPa и остается постоянным в интервале 2 ≤ x ≤ 4 мм. Затем τ падает до нуля. При удалении от оси влево τ меняется аналогично.
T, MPa 25 20 15 10
б)
-6 -4 -2 0 2 *, мм
а)
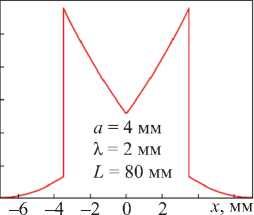
Рис. 9. Распределения τ в 6-угольном сечении: а — сила направлена вдоль большой диагонали; б — сила на правлена вдоль малой диагонали
При повороте звезды на 30° распределение напряжения τ существенно меняется, приобретая очертания ласточкиного хвоста (рис. 9 б ). Наблюдаются два пика со значением τ max = 28,12 MPa. Картина распределения симметрична. Однако при удалении от оси симметрии напряжение сначала увеличивается от 12,5 до 28,12 MPa, а затем падает до 3,125 MPa. В связи с этим на зависимости τ( x ) наблюдаются два пика. Далее напряжения быстро уменьшается до нуля.
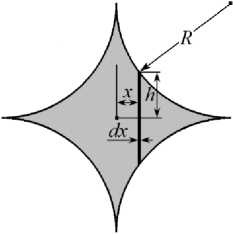
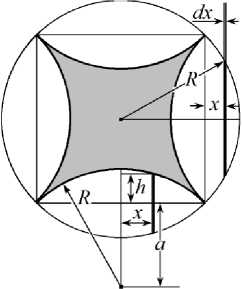
Фигурный крест. Рассмотрим решение для момента инерции нестандартного сечения в виде фигурного креста (рис. 10), каждая сторона которого является четвертой частью окружности радиуса R . Расстояние между вершинами фигуры равно R √2. Найдем сначала момент инерции креста относительно большой диагонали (рис. 10 а ).
а)
б)
Рис. 10. Фигурный крест: а — сила направлена вдоль диагонали креста; б — сила направленна под углом 45° к диагонали креста
Половина длины полоски h на рис. 10 а равна
h = R - R2 - (R - x)2.
Учитывая симметрию и используя уравнение (3), получим следующее значение момента инерции сечения фигурного креста:
R 3
I x =j J [ R — V x( 2 R — x) ] dx = [ 4 — 5 n / 4 ] R 4 .
Определим момент инерции креста при повороте его на 45° относительно оси x (рис. 10 б ).
Фигурный крест вписывается в окружность радиуса R . Из рис. 10 б видно, что вокруг креста выделяются четыре фигуры в виде овала с острыми углами. Для определения момента инерции креста достаточно из момента инерции круга вычесть моменты инерции четырех овалов.
Из (6) следует, что момент инерции круга равен:
I x 0 =n R 4/4 .
Определим моменты инерции овалов относительно центра тяжести креста.
Момент инерции овала справа равен моменту инерции овала слева. Полувысота полоски у овала слева:
h1 = JR2 — (R — x)2.
Учтем уравнение (3), а также симметричность данных частей и их расположения. Интегрированием от 0 до R – R /√2 получим следующее значение момента инерции данных двух частей:
g^ 3 R( 1 — 1 / V2 ) I x 1 =
з
[ 71 — ( 1 — x/R) 2 J dx = —
3п
—
2 .
Центры тяжести овалов сверху и снизу окружности расположены на расстоянии a = R /√2 от центра тяжести целой фигуры. Площадь этих двух частей равна S = R 2(π – 2).
По (4) вычислим момент инерции данной пары:
Ix2 = a2S = R4 [П2 — 1].
Величина h в (3), согласно рис. 10 б , (овал внизу круга) равна h = л/ 2 a 2
— x —
a . Следовательно, для пары
овалов сверху и снизу круга можно записать момент инерции относительно собственных центров тяжести:
л = 8 R 3 x 3 3
R/ 2 3
J ^1 — ( x/R ) 2 — 1 / V2 dx = R 4 [ 3 n / 4 — 7 / 3 ] .
Механика
Определим результирующий момент инерции фигурного креста. Для этого из момента инерции (13) круга вычтем моменты инерции четырех овалов:
I x 0 - I x 1 - I x 2 - 2 I x 3 = [ 4 - 5П/4 ] R 4 .
Сравнивая полученный результат с результатом (13), убеждаемся, что момент инерции данного крестообразного сечения консоли не меняется при повороте оси x на 45°.
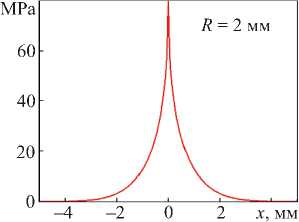
На рис. 11 а показано распределение напряжения сдвига в сечении фигурного креста, соответствующее λ = 2 мм и действию внешней приложенной силы вдоль оси креста (рис. 10 а ). На вертикальной оси креста наблюдается острый пик напряжения, где τ max = 80,0 MPa.
а)
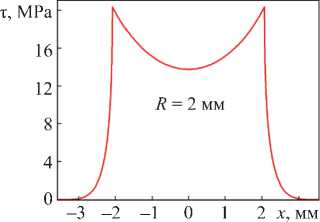
Рис. 11. Распределения τ в сечении фигурного креста: а — сила направлена вдоль диагонали креста;
б — сила направлена под углом 45° к диагонали креста
б)
При повороте креста относительно приложенной силы на 45° распределение напряжения τ существенно меняется. По мере отклонения оси симметрии напряжение сначала плавно увеличивается с τ = 13,73 MPa до τ max = 20,32 MPa. Затем напряжение τ резко падает до нуля. Поэтому в распределении τ наблюдается два симметричных пика (рис. 11 б ) на расстоянии 2 мм от оси симметрии.
Обсуждение и заключение. Предложенный упрощенный метод расчета позволяет быстро узнать моменты инерции сложных поперечных сечений консоли. При этом однозначно определяется поле напряжения сдвига в сечении образца, соответствующее действию внешней приложенной силы. Кроме того, показано, что распределение напряжений в сечении качественно и количественно зависит от ориентации сечения относительно направления внешней приложенной силы.
Для обоснования метода проведены вычисления моментов инерции не только для известных сечений простой геометрической формы (которые показали абсолютную идентичность расчетных и опубликованных в литературе результатов), но и для двух новых сложных сечений в виде правильной шестиконечной звезды и фигурного креста. Показано, что жесткость консоли не меняется при повороте внешней силы, приложенной перпендикулярно оси симметрии, на 30° для сечения в виде 6-конечной звезды, и на 45° — для квадрата и фигурного креста. Метод и полученные решения могут быть использованы инженерами и механиками при моделировании и расчетах прочности и жесткости стержневых элементов конструкций.
Список литературы Упрощенный расчет момента инерции поперечного сечения консоли под нагрузкой
- Ching Francis DK, Onouye B, Zuberbuhler D. Building Structures Illustrated: Patterns, Systems, and Design. 2nd ed. Hoboken, NJ: John Wiley & Sons; 2014. 352 p. URL: https://zlib.pub/book/building-structures-illustrated-1rgfde22jln8 (accessed: 22.02.2024).
- Hallebrand E, Jakobsson W. Structural Design of High-Rise Buildings. Lund: Media-Tryck LU; 2016. 142 p.
- Amany D, Pasini A. Material and Shape Selection for Stiff Beams under Non-Uniform Flexure. Materials and Design. 2009;30(4): 1110-1117. http://doi.org/10.1016/j.matdes.2008.06.029
- Pilkey WD. Formulas for Stress, Strain, and Structural Matrices. Hoboken, NJ: John Wiley & Sons; 2005. 1536 p.
- Гайджуров П.П., Савельева Н.А. Применение метода двойной аппроксимации для построения матриц жесткости объемных конечных элементов. Advanced Engineering Research (Rostov-on-Don). 2023;23(4):365-375. https://doi.org/10.23947/2687-1653-2023-23-4-365-375; Gaidzhurov PP, Saveleva NA. Application of the Double Approximation Method for Constructing Stiffness Matrices of Volumetric Finite Elements. Advanced Engineering Research (Rostov-on-Don). 2023;23(4):365-375. https://doi.org/10.23947/2687-1653-2023-23-4-365-375
- Murakami Y. Theory of Elasticity and Stress Concentration. Hoboken, NJ: John Wiley & Sons; 2016. 480 p. URL: https://www.wiley.com/en-us/Theory+of+Elasticity+and+Stress+Concentration-p-9781119274100 (accessed: 22.02.2024).
- Bechtel FK. Estimating Local Compliance in a Beam from Bending Measurements. Part I. Computing "Span Function". Wood and Fiber Science. 2007;39(2):250-259. URL: https://wfs.swst.org/index.php/wfs/article/view/1344/1344 (accessed: 22.02.2024).
- Bhattachaijya RK. Engineering Mechanics. New Delhi: Oxford University Press; 2009. 832 p.
- Damkilde L. Stress and Stiffness Analysis of Beam Sections. Copenhagen: Technical University of Denmark; 2000. 36 p.
- Жернаков В.С. Сопротивление материалов — механика материалов и конструкций. Уфа: Уфимский государственный авиационный технический университет; 2012. 495 с. URL: https://mircompozitov.ucoz.ru/ld/3/306 Zhernakov.pdf (дата обращения: 22.02.2024). Zhernakov VS. Material Resistance — Mechanics of Materials and Structures. UFA: Ufa State Aviation Technical University; 2000. 36 p. (In Russ.).
- Kleppner D, Kolenkow R. An Introduction to Mechanics. 2nd ed. Cambridge: Cambridge University Press; 2014. 566 p.
- Паньженский В.И., Сурина О.П., Сорокина М.В. Аналитическая геометрия на плоскости. Пенза: Изд-во Пензенского государственного университета; 2020. 120 с. Pan'zhenskii VI, Surina OP, Sorokina MV. Plane Analytic Geometry. Penza: Penza State University; 2020. 120 p. (In Russ.).
- Brown RG. Introductory Physics I. Elementary Mechanics. Durham: Duke University Physics Department; 2013. 661 p.


