Упругие постоянные двумерного коллоидного кристалла в модели уравнения пуассона-больцмана

двумерного электрически стабилизированного коллоидного кристалла с квадратной решеткой. Электростатическое взаимодействие макрочастиц в ней полностью описывается нелинейным уравнением Пуассона-Больцмана [5,6]. Помимо этого не делается никаких дополнительных предположений о характере межчастичного взаимодействия, в частности, оно априори не предполагается парным. Все макроскопические свойства коллоидного кристалла, обусловленные электростатическим взаимодействием его частиц, выводятся исключительно из решений уравнения ПБ и соответствующего ему тензора напряжений.

В работе средствами вычислительного эксперимента на основе численного решения уравнения Пуассона-Больцмана находятся упругие постоянные 1-го и 2-го порядка Нахождение упругих постоянных основывается на определении зависимости напряжения от деформации. Для электрически стабилизированных коллоидных кристаллов такой подход ранее не применялся. Уравнение Пуассона-Больцмана для каждой пространственной конфигурации решается методом конечных элементов. Наличие пространственной симметрии как в исходной конфигурации, так и при наложении деформации дает возможность ограничиться рассмотрением всего одной элементарной ячейки. Платой за это является необходимость использовать периодические граничные условия для потенциала и его градиента.

Элементарная ячейка исследуемого в данной работе двумерного коллоидного кристалла показана на рисунке 1. Кристалл образован бесконечно длинными цилиндрическими частицами радиуса R , расположенными в узлах квадратной решетки Бравэ. В силу того, что в направлении вдоль оси частиц свойства системы не ме-

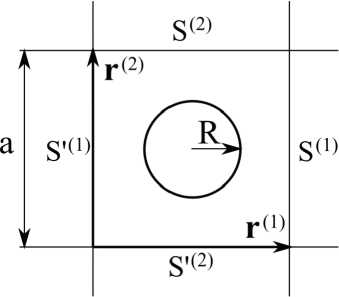
Рис. 1. Ячейка Вигнера-Зейтца двумерного электрически стабилизированного коллоидного кристалла с квадратной решеткой няются, система может рассматриваться также как система двумерных жестких дисков на плоскости. Векторы r(1) и r(2) — векторы примитивных трансляций; величина a = |r(1)| = |r(2)| называется параметром решетки. Система частиц погружена в жидкий электролит. Частицы являются абсолютно твердыми диэлектриками. Частицы электрически заряжены, при этом на поверхности частиц поддерживается постоянный электрический потенциал фр = const.

Показанная на рис. 1 элементарная ячейка является ячейкой Вигнера-Зейтца кристалла в исходном состоянии. При наложении деформации ячейка деформируется вместе со всем кристаллом, при этом деформированная ячейка снова является элементарной ячейкой, хотя, возможно, уже и не ячейкой Вигнера-Зейтца. Все обозначения остаются в силе и для деформированной ячейки.

Электрический потенциал ϕ в области электролита описывается нелинейным дифференциальным уравнением Пуассона-Больцмана, которое в общем случае имеет вид [5,6]

V2ф = — £ ziqen0i exp (- z^eV/kT), (1) £ о£ i где £0 - электрическая постоянная, £ - диэлектрическая проницаемость электролита, qe – элементарный заряд, zi – валентность i -ой компоненты электролита, n0i - объемная концентрация i-ой компоненты электролита в объеме, то есть в области вдали от заряженных частиц, где потенциал принимается равным нулю, k – постоянная Больцмана, T – абсолютная температура. Суммирование в (1) осуществляется по всем компонентам электролита. В дальнейшем рассматривается случай бинарного симметричного одновалентного электролита, или 1:1 электролита, для которого уравнение Пуассона-Больцмана наиболее применимо. Таким образом, электролит имеет две компоненты с валентностями z 1 = +1 и z2 = —1, при этом n01 = n02 = n0 .

Для приведения уравнения и всех последующих выражений к безразмерному виду вводятся следующие величины: длина Дебая для 1:1 электролита к^-1 = ( 2 n ₀ q e/ £ ₀ £ kT )^{— 12} для измерения длины и величина kT q _e для измерения электрического потенциала. В этих единицах уравнение Пуассона-Больцмана для исследуемой системы записывается в следующей безразмерной форме:

V ² ф = sh ф . (2)

Уравнение (2) описывает распределение электрического потенциала ϕ в области электролита. Для одной элементарной ячейки эта область ограничена, во-первых, поверхностью частицы S , и, во-вторых, внешней границей ячейки. Внешняя граница образована парами противолежащих сторон S ⁽¹⁾ , S ' ⁽¹⁾ и S ⁽²⁾ . S ' ⁽²⁾ , так, как показано на рисунке 1. Граничные условия на поверхности S частицы определяются заданием постоянного электрического потенциала ϕ _p на ней:

^V S = ф р . (3)

На внешней границе ячейки в силу пространственной периодичности кристалла выполняются периодические граничные условия для потенциала:

ф ( г ) = ф ( г + r ⁽ m ) ) , r g S ^{,( m} ) , m = 1,2 , (4) и нормальной компоненты градиента потенциала:

Vv(r) • n'( m) = —Vv(r + r(m)) • n( m), r g S"m), m = 1,2. (5)

Здесь m – номер пары противолежащих границ, n ^{( m} ) и n ' ^{( m} ) - внешние единичные нормали соответствующих отрезков границы. Электрический потенциал ϕ в любой мгновенной конфигурации кристалла, как исходной, так и деформированной, определяется решением краевой задачи для уравнения (2) в области электролита с граничными условиями (3), (4) и (5).

Важной особенностью упругих свойств электрически стабилизированных коллоидных кристаллов, отличающей их от обычных кристаллов, является наличие ненулевого механического напряжения в исходной конфигурации, то есть даже при отсутствии деформации. Это напряжение необходимо для компенсации взаимного отталкивания одноименно заряженных коллоидных частиц. В кристалле с квадратной решеткой рассматриваемого в данной работе типа в силу очевидной симметрии начальное напряжение изотропно и сводится к (осмотическому) давлению. При этом разложение в ряд Тейлора зависимости напряжения T_ij от деформации с точностью до линейных членов имеет вид [7]

T ij = p ^ ij ⁺ B_y kl ⁸ kl . (6)

Здесь 5 j - символ Кронекера, p - напряжение в исходной конфигурации при отсутствии деформации, 8 j - тензор бесконечно малых деформаций (вклад тензора бесконечно малых вращений, требуемый в общем случае, в силу изотропии начального напряжения равен нулю), B_ijkl – тензор упругости, компоненты которого называются модулями упругости. Для кристалла с квадратной решеткой имеется только три нетривиальных модуля упругости: B ₁₁₁₁ , B ₁₁₂₂ , B ₁₂₁₂ . Остальные модули могут быть получены по симметрии путем перестановки индексов, либо равны нулю. В данной работе для коллоидного кристалла определяются упругие постоянные двух типов [8]: начальное давление p (упругая постоянная первого порядка) и модули упругости B ₁₁₁₁ , B ₁₁₂₂ , B ₁₂₁₂ (упругие постоянные второго порядка).

Напряжение T_ij вычислялось с помощью тензора напряжений n j согласно процедуре, изложенной в [9]. Тензор n j описывает локальное напряжение в системе, электрический потенциал которой подчиняется дифференциальному уравнению Пуассона-Больцмана. В безразмерной форме для бинарного симметричного одновалентного электролита он имеет вид

П = Vф®Vф - (у |V ф |² + ch ф - 1) I . (7) где ф = ф^г ) - решение краевой задачи для электрического потенциала, I – единичный тензор. На основании [9] напряжение T_ij в случае квадратной ячейки Вигнера-Зейтца вычисляется следующим образом:

Р = "Р i ds j . a S (1)

Давление в исходной конфигурации определялось по формуле (9). Для нахождения модулей упругости коллоидный кристалл подвергался деформациям двух типов: растяжение вдоль оси x вида

и сдвиг вида

^ ii

0 )

V

0 У

A

V ⁸ 21

о У

’ ⁸ 12 = ⁸ 21 ’

который эквивалентен растяжению в направлении под углом 45 ° к оси x и сжатию в перпендикулярном направлении. При таких деформациях с точностью до линейных членов справед-

ливы выражения

T 11 =   ^{р +} B 1111 ⁸ 11 ’

T 22 = p ⁺ B 2211 ⁸ 11 = p ⁺ B 1122 ^e 11 ,

^T 12    B 1212 ⁸ 12 ⁺ B 2121 ⁸ 21    ^{2 В} 1212 ^£ 12 ,

(12a) (12b)

(12c)

при записи которых использовались свойства симметрии коэффициентов B j _kl : B 2121 = B ₁₂₁₂ и B ₂₂₁₁ = B ₁₁₂₂ (последнее справедливо только для изотропного начального напряжения). Для определения модулей упругости в ходе вычис-

T ik 2

a ²

r k ¹

V

)

J ^П jj r k ) Jⁿ y ds j

S (1)

S (2)

,

У

где a - период решетки, n j - компоненты тензора, задаваемого формулой (7), r ⁽¹⁾ и r ⁽²⁾ – векторы квадратной решетки Бравэ, разделяющие пары противоположных границ ячейки, S ⁽¹⁾ и S ⁽²⁾ – границы ячейки по которым производится интегрирование (см. рис. 1). Стоит отметить, что интегрирование осуществляется только по одной из каждой пары противоположных границ ячейки; ориентация границ определяется направлением внешней нормали. Подразумевается суммирование по повторяющимся индексам.

Выражение (8) позволяет вычислить напряжение как для случая исходной, так и для произвольно деформированной ячейки. Для исходной квадратной ячейки в силу ее симметрии возможны дальнейшие упрощения, которые позволяют получить следующее выражение для начального изотропного давления p :

лительного эксперимента исследовались зависимости T 11 ( 8 11 ) , T 22 ( 8 11 ) , T ₁₂ ( f ₁₂ ) напряжений от деформаций. Численные значения деформации изменялись в диапазоне 8 ₁₁ = - 0,01 - 0,01 с шагом 0,001 и 8 ₁₂ = - 0,005 ^ 0,005 с шагом 0,0005 . Напряжения вычислялись по формуле (8). Затем осуществлялась полиномиальная аппроксимация полученных зависимостей стандартным методом наименьших квадратов. Коэффициент при линейном члене аппроксимации в соответствии с формулами (12a), (12b) и (12c) давал значение соответствующего модуля упругости.

Моделирование упругих свойств коллоидно-

го кристалла проводилось при следующих значениях параметров: радиус частицы R = 1 , постоянный потенциал на поверхности частицы

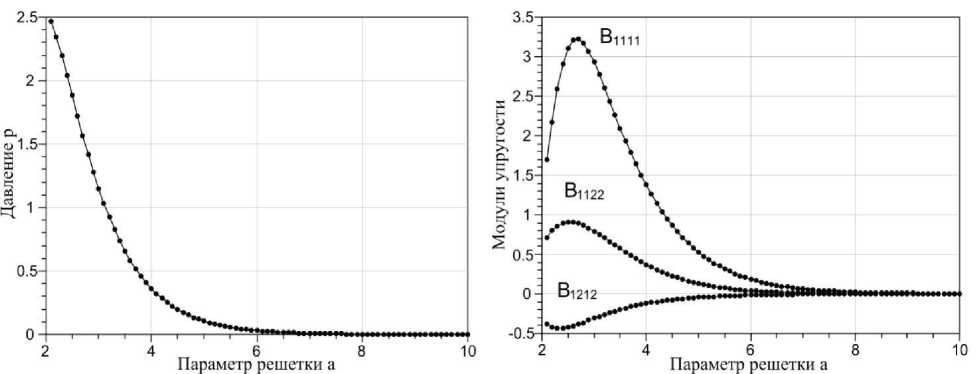
ф _р = 2 . Параметр решетки а изменялся в диапазоне от 2,1 (почти контакт частиц) до 10 (взаимодействие частиц исчезающее мало). Результаты моделирования представлены на рис. 2.

Анализ результатов показывает, что при увеличении плотности системы давление в исходной конфигурации монотонно растет. В то же время на кривых для модулей упругости наблюдается спад при малых значениях параметра решетки. Это объясняется особенностью модели поведения заря-

(а)                                                     (б)

Рис. 2. Упругие постоянные двумерного коллоидного кристалла с квадратной решеткой при R = 1 , ϕp = 2, (а) – напряжение в исходной конфигурации, (б) – модули упругости да на частице: для поддержания постоянного потенциала заряд перемещается по поверхности и даже покидает ее, что приводит к уменьшению жесткости кристалла при высоких плотностях. Отрицательные значения модуля упругости B1212 свидетельствует о механической неустойчивости рассматриваемого типа кристалла по отношению к деформации сдвига. Это связано с сильным экранированием в электрически стабилизированных коллоидных системах, приводящим к быстрому спаданию с расстоянием силы межчастичного взаимодействия, а также с тем, что в квадратной решетке расстояние между ближайшими соседями 2го порядка значительно, в 2 раз, больше расстояния между ближайшими соседями 1-го порядка. Неустойчивость двумерного кристалла рассматриваемого типа к деформации сдвига может пролить свет на то обстоятельство, что в реальных условиях системы частиц с квадратной решеткой формируются преимущественно вблизи подложки [10].