Упругие постоянные монослойного электрически стабилизированного коллоидного кристалла с квадратной решеткой

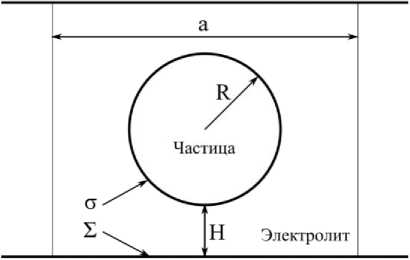
пластинами. Расстояние от края частиц до пластин с обеих сторон одинаково и равно H . Частицы и пластины в общем случае электрически заряжены с постоянной поверхностной плотностью заряда σ и Σ соответственно. Центры коллоидных частиц расположены в узлах двумерной квадратной решетки с параметром a . Свободное пространство между пластинами и частицами заполнено электролитом. Свойства коллоидного кристалла рассматриваются в приближении статической решетки, при котором тепловым движением частиц пренебрегается.

Пластина

Пластина

Рис. 1. Элементарная ячейка монослойного коллоидного кристалла

Электростатический потенциал ϕ в области электролита описывается нелинейным дифференциальным уравнением Пуассона-Больц-мана [7,8]. Для двухкомпонентного электролита это уравнение имеет вид

^^Ф =--~ ( z 1 q e n 01 e" z ¹ ^kT + z 2 q e n 02 e" z2^^ )

S o S^V

,

где ε 0 – электрическая постоянная, ε – относительная диэлектрическая проницаемость электролита, q e – элементарный заряд, k – постоянная Больцмана, T – абсолютная температура. В дальнейшем рассматривается случай бинарного симметричного одновалентного электролита, или 1:1 электролита, для которого уравнение Пуассона-Больцмана является хорошим приближением. Такой электролит имеет две компоненты с валентностями z 1 =+1 и z₂=–1, при этом объемные концентрации обеих компонент в невозмущенном электролите равны друг другу: n 01 = n 02 = n 0 .

Для приведения уравнения и всех последующих выражений к безразмерному виду вводятся следующие величины: длина Дебая для 1:1 электролита к ^-1 = ( 2 n ₀ q^ /s₀£kT ) для измерения длины и величина kT / q_e для измерения электрического потенциала. В этих единицах уравнение Пуассона-Больцмана для исследуемой системы записывается в следующем безразмерном виде:

У2ф =shф

Предполагается, что диэлектрическая проницаемость электролита велика по сравнению с диэлектрической проницаемостью материала частиц и пластин, что типично для электролитов на водной основе. В этом случае электрический потенциал ϕ на поверхности частиц удовлетворяет граничному условию Неймана вида

—^ф- n = о

а на поверхности пластин граничному условию Неймана вида

-^ф-n = 2

где ⁿ – вектор единичной нормали, направленный внутрь электролита.

В силу пространственной периодичности, как в исходной конфигурации, так и при наложении деформации, при нахождении электрического потенциала можно ограничиться рассмотрением только одной элементарной ячейки. Для исходной конфигурации в качестве области определения задачи выбиралась ячейка Вигнера-Зейтца одной из частиц. Эта ячейка представляет собой прямоугольный параллелепипед с квадратным основанием размером а х а и высотой 2( H + R ). Коллоидная частица находится в центре ячейки. При наличии деформации область определения получается соответствующей трансформацией исходной ячейки. Уравнение (2) справедливо во всей ячейке за вычетом объема частицы.

На боковых гранях области определения задачи в силу пространственной периодичности кристалла выполняются периодические граничные условия для потенциала:

ф( r ) = ф(г + r( m)) m = 1,2

,

и нормальной компоненты градиента потенциала:

V ф ( r ) - n ⁽ " ' = -^ф(г + r ^{( m} ' ) - n ' - ¹     „ = 1,2

^,          (6)

.

Здесь m – номер пары противолежащих границ, n ⁽ m ) и n '⁽ m ) — внешние единичные нормали соответствующих участков границы, а векторы r ^(m) — векторы примитивных трансляций, разделяющие симметричные точки на противолежащих границах.

Для нахождения упругих постоянных кристалл подвергается деформациям только в направлениях, параллельных пластинам. При этом сохраняется зеркальная симметрия относительно срединной горизонтальной плоскости, проходящей через центры частиц. По этой причине в вычислениях использовалась только половина (нижняя) элементарной ячейки. На плоскости зеркальной симметрии в этом случае выполняется однородное граничное условие Неймана

-^ф-n = 0

Таким образом, нахождение электрического потенциала ϕ в любой мгновенной конфигурации кристалла, как исходной, так и деформированной, определяется решением краевой задачи для уравнения (2) в указанной области с граничными условиями (3), (4), (5), (6) и (7) на ее границах.

Решение краевой задачи осуществлялось методом конечных элементов с использованием градиентных нерегулярных сеток тетраэдральных элементов. Работа выполнена с использованием ресурсов суперкомпьютерного комплекса МГУ имени М.В. Ломоносова [9]. По отношению к боковым деформациям исследуемый кристалл может рассматриваться как двумерная система. Как двумерная система кристалл обладает тремя нетривиальными упругими постоянными 2-го порядка: модулями упругости B 1111 , B 1122 , B 1212 , а также одной упругой постоянной 1-го порядка: B ₁₁. Последняя обусловлена наличием напряжения даже в исходной конфигурации при отсутствии деформации и сводится к изотропному исходному давлению: B 11 =– p . Индексы 1 и 2 в обозначении упругих постоянных обозначают компоненты в двумерной декартовой системе координат, расположенной в срединной плоскости системы.

Для нахождения модулей упругости оказывается достаточным деформаций двух типов: растяжение вдоль оси x вида

5,1

I 00 и сдвиг вида

[ 0

V5 21

При этом справедливы следующие выражения для зависимости напряжений от деформаций:

т T11 = — p + Snnfn +... , (10) т 22 = — р + B1122^11 + ... , (11) т 12 = ?/?      4- 2В1212Ъ12 + е * * , (12) где многоточие обозначает члены более высоких порядков по деформации, и учтено, что для кристалла рассматриваемого типа B2121=B1212 и B2211=B1122 [5], а также, что 821=£12.

Тензор напряжений T ij в ( 10) - (12) описывает напряжение в двумерной системе, то есть рассчитывается на единицу длины. Его компоненты получаются из компонент обычного (на единицу площади) тензора осмотического напряжения S ij умножением на высоту ячейки:

T , = 2 ( H + R ) S ,

Осмотическое напряжение Sj вычисляется с помо- щью фундаментального тензора напряжений [10] по формуле

П

5„ = у Z r m ¹ J П ,^

^Vc ^m      S ( m )

Здесь Vc - объем элементарной ячейки, r(m) - вектор примитивных трансляций, разделяющий эквивалентные точки каждой пары m противолежащих граней ячейки, а интегрирование осуществляется по одной из двух граней в каждой паре. Нормали на всех внешних гранях направлены наружу. Тензор П в случае 1: 1 электролита имеет вид

П = Уф®Уф—(1 УФ2 + ch ф —1) I где I - единичный тензор.

В ходе вычислительного эксперимента для каждого фиксированного набора параметров σ , Σ, R, H и а модели определялись зависимости T₁₁(s₁₁),T ₂₂( s ₁₁) и T ₂₁( s ₁₂). Численные значения деформации изменялись в диапазоне 8 ₁₁=-0,01^0,01 и е₁₂=0^0,01 с шагом 0,001. На каждом шаге деформации строилась определяемая ею область задачи и решалась соответствующая краевая задача. Напряжения вычислялись по полученному решению краевой задачи с помощью формул (13), (14) и (15). Затем осуществлялась полиномиальная аппроксимация полученных зависимостей стандартным методом наименьших квадратов. Коэффициент при линейном члене аппроксимации в соответствии с формулами (10) - (12) давал значение соответствующего модуля упругости, а постоянный член — минус равновесное давление. Моделирование упругих свойств коллоидного кристалла проводилось при следующих значениях параметров модели: ^ =2; Е=0; R =1; H =1. Параметр решетки а изменялся в диапазоне 2,1÷6,0 с шагом 0,1. Результаты моделирования представлены на рис. 2.

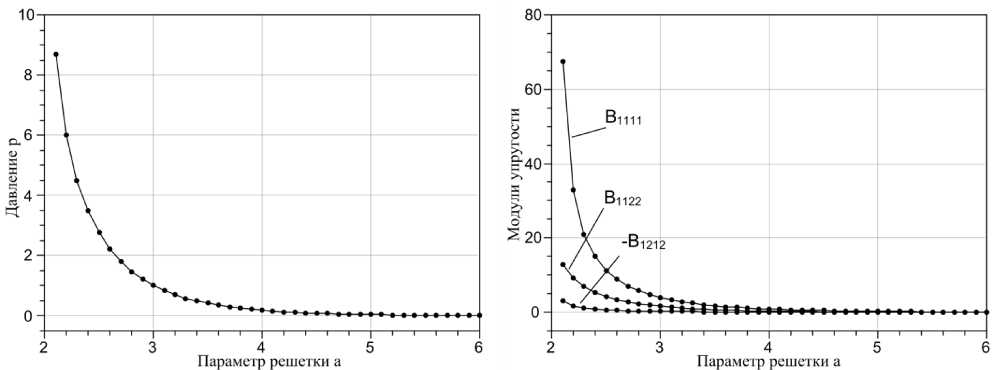
Рис. 2. Равновесное давление и модули упругости монослойного коллоидного кристалла

Анализ данных на рис. 2 показывает, что осмотическое давление изменяется монотонно во всем диапазоне исследованных значений параметра условной кубической ячейки. При увеличении плотности давление резко возрастает. Поведение модулей упругости носит аналогичный характер. Модуль B1212 остается отрицательным во всем исследованном диапазоне значений параметра а. Это свидетельствует в пользу того, что кристалл рассматриваемого типа в рамках принятой модели неустойчив по отношению к деформации сдвига. Ранее такой же результат наблюдался для анало- гичной модели двумерного коллоидного кристалла [11].

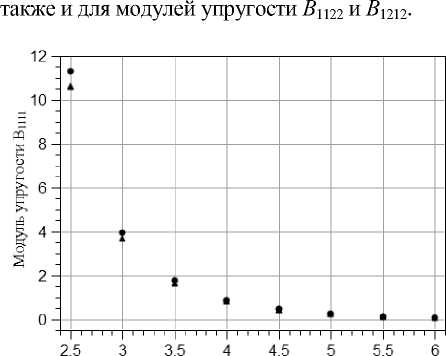
Результаты моделирования модулей упругости, полученные вышеописанным методом, сравнивались со значениями модулей упругости, вычисленными через силовые постоянные кристалла. Методика определения силовых постоянных аналогична той, что использовалась в [12]. На рис. 3 представлены данные для модуля упругости B1111, полученные обоими методами. Имеет место хорошее согласие результатов. Небольшие отклонения в значениях в значительной мере объясняются тем, что при вычислении модулей упругости через силовые постоянные учитывались вклады ближайших соседей только до второго порядка включительно; вклады соседей более высоких порядком незначительны по величине и трудноопределимы численно. Хорошее согласие данных наблюдалось

Параметр решетки а

Рис. 3. Сравнение значений модуля упругости B₁₁₁₁, полученных различными методами. Кружки – по зависимости напряжения от деформации, треугольники – через силовые постоянные