Упругие свойства и механическое поведение неоднородно набухших сетчатых эластомеров и полимерных гелей

The equations and constitutive relations describing elastic properties and mechanic behavior of materials contained liquid under finite strain are formulated. The stress-strain state and elastic response of non-uniform swollen slab of polymer gel are studied.

Объектами исследования в данной работе являются эластомеры и полимерные гели. На молекулярном уровне такие материалы представляют собой пространственную сетку, состоящую из длинных и гибких макромолекулярных цепей, соединённых между собой химическими связями [4]. Межцепное пространство полимерной сетки может заполнять низкомолекулярная жидкость (растворитель).

Как известно, такие материалы могут испытывать большие обратимые упругие деформации. Они способны поглощать органические и неорганические растворители, многократно (в десятки и сотни раз) увеличиваясь в объёме. При этом полимерная сетка препятствует их растворению в жидкости, поэтому они лишь ограниченно набухают. В набухшем состоянии сохраняют свою форму и способность к обратимым упругим деформациям (свойство высокоэластичности). Наличие данных свойств объясняется их структурой.

Благодаря своим качествам полимерные гели и эластомеры находят применение во многих современных технологиях: в биотехнологиях, медицине, сельском хозяйстве, ландшафтном дизайне и т.д. [1–3]. Изделия на основе эластомеров (полиуретановые валки, дозирующие мембраны в лакокрасочной промышленности, защитные покрытия, масло- и трубопроводы, уплотнительные элементы и т.д.) предназначены для эксплуатации в физически агрессивных средах – органических растворителях и их парах.

Внутри материала в ходе поглощения растворителя и его набухания возникают значительные градиенты концентрации растворителя, которые порождают большие деформации и сложнонапряженное состояние. В связи с этим возникает необходимость учитывать и изучать подобного рода явления при проектировании технологических процессов и режимов эксплуатации изделий из полимерных материалов в агрессивных средах.

Данная работа посвящена исследованию упругих свойств и механического поведения сетчатых эластомеров и полимерных гелей, содержащих растворитель. Формулируется общая система уравнений, описывающих напряжённо-деформированное состояние нелинейно-упругого материала с неоднородным распределением растворителя. Общая теория иллюстрируется на примере неоднородно набухшего плоского слоя эластомера или полимерного геля.

Механика и термодинамика упругих материалов, содержащих жидкость

Рассмотрим образец полимерного геля или эластомера с заданным в его объеме неоднородным распределением растворителя, который подвергнут механическому нагружению. Внешние механические нагрузки, действующие внутри материала, и неоднородное распределение растворителя порождают в нем напряжённо-деформированное состояние.

Сформулируем общую систему уравнений, описывающих это напряжённо-деформированное состояние. Уравнения равновесия выведем из вариационного принципа, который сформулируем на основе законов термодинамики.

В качестве отсчетного выберем механически ненагруженное состояние образца, в котором жидкость распределена однородно. Пусть Ω ⁰ – область пространства, которое занимает материал в этом состоянии. В результате механического нагружения и взаимодействия с растворителем он переходит в деформированное состояние, и Ω – область пространства, занимаемого им в этом состоянии. Будем полагать, что на части границы полимерного геля Γ ₁ ⁰ ⊂ ∂Ω ⁰ (в отчётной конфигурации) действуют поверхностные силы g ⁰ . В текущей конфигурации они описываются векторным полем g , которое определено на поверхности Γ ₁ ⊂∂Ω , являющейся образом Γ ₁⁰ . Положение в пространстве остальной части границы материала Γ ⁰ ₂ =∂Ω ⁰\ Γ ₁ ⁰ , образом которого является Γ ₂ =∂Ω \ Γ ₁ , задано и определяется в отсчетном и деформированном состоянии функциями r = r * ( q^k ) и R = R * ( q^k ) соответственно. При этом q^k , k = 1, 3 -система материальных координат, связанная с упругой матрицей.

Согласно второму закону термодинамики изменение энтропии смеси (упругой среды, насыщенной жидкостью) ∆ S должно удовлетворять неравенству T ∆ S ≥ Q , где T – температура окружающей среды, играющей роль термостата, Q – количество теплоты, полученное смесью от термостата.

Если система находится в состоянии устойчивого равновесия, то самопроизвольный переход в другие (соседние) состояния термодинамически невозможен. Это выражается неравенством (по Гиббсу)

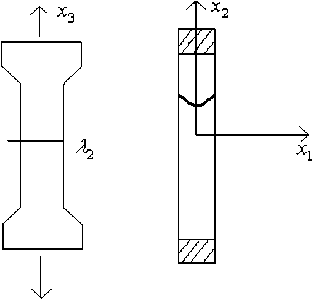
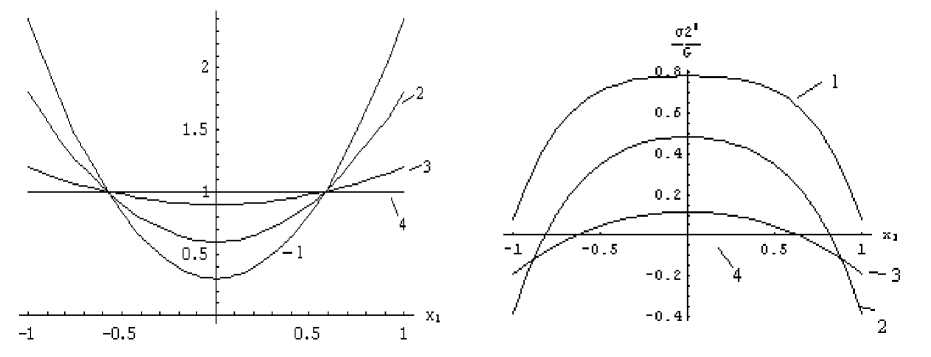
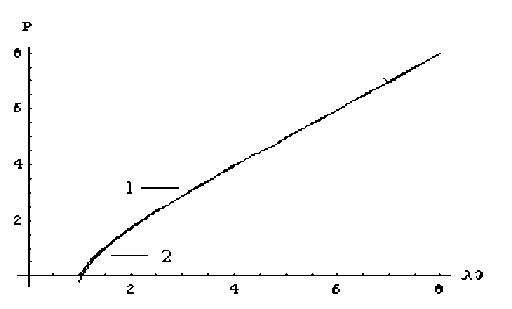
T∆S

По первому закону термодинамики изменение внутренней энергии смеси ∆U=Q+A,(2)

где U – внутренняя энергия смеси, A – работа поверхностных сил.

Выразив из (2) величину Q и подставив ее в (1), получим

∆F -A >0 ,(3)

где F =U-TS – свободная энергия смеси.

Входящие в неравенство (3) величины являются функционалами следующего вида:

AF = F (JR, N1) - F (R, N1), F (R, N1) = f f 0dV0, A(IR, AR) =J g⁰ ■ 5RdS0.

Ω⁰                                 Γ₁⁰

Здесь f⁰ – плотность свободной энергии смеси, отнесённая к единичному объёму отсчётной конфигурации; N₁- функция, зависящая от материальных координат и описывающая распределение жидкости в деформированном материале.

Решение вариационного неравенства (если оно существует и все входящие в него функционалы обладают достаточной   гладкостью)   должно удовлетворять вариационному уравнению (4), смысл которого заключается в обращении в ноль линейной части неравенства (3), то есть обращении в ноль первой вариации.

JF -j g⁰■ 5RdS⁰= 0.                                        (4)

r0

Отсчетная конфигурация варьированию не подвергается, поэтому 6F = б V R = V 6R.

Используя тождество P : 6FT = V- (P ■ 6R) - ( V- P) ■ 6R , теорему Гаусса – Остроградского и 5R(q^k) = 0 при r(q^k ) e Г2 , получим

V     ⁷N1, n₂

матрицы, n⁰– внешняя нормаль в отсчетной конфигурации.

Представив систему уравнений в текущей конфигурации, получаем следующую краевую задачу:

V-T = 0, J = J*(qk), R eQ ;(6)

n■ T = g, (R e Г1); R = R.(qk), (R e Г2);(7)

T = FT ■ (df/dF)n1,n2 -pE ,(8)

где T = J-1FT ■ P - тензор напряжений Коши; F - тензор градиента деформации; J = det F - третий инвариант градиента деформации; функция J*( qk), характеризующая распределение растворителя в объеме материала; E – единичный тензор; n – внешняя нормаль в текущей конфигурации; p – действующее в смеси гидростатическое давление; f – плотность свободной энергии в деформированном состоянии; n1 , n2 – концентрации растворителя и упругой матрицы в текущем состоянии смеси соответственно.

Будем рассматривать несжимаемую смесь. Условие несжимаемости смеси имеет вид [6]

J = Ф0/Ф2,                                                  (9)

где ф₂, ф0 - объёмная доля упругой матрицы соответственно в отсчётной и текущей конфигурации.

Условие (9) означает, что единственной причиной объемных деформаций материала является поглощение растворителя.

Следует отметить, что задача, описываемая системой уравнений (6) – (8), является естественным обобщением задачи Эйлера–Лагранжа для несжимаемого материала. В случае однородного распределения растворителя J = 1 она оказывается полностью аналогичной статической задаче теории упругости для несжимаемого материала.

В качестве примера рассмотрим неоднородно набухший плоский слой эластомера или полимерного геля в условиях одноосного растяжения в одном из продольных направлений (рис.1, а). Найдем упругую реакцию образца и его напряженно-деформированное состояние.

а            б

Рис.1. Плоский слой эластомера или полимерного геля с неоднородным распределением растворителя (а) в условиях одноосного растяжения (б)

Примем следующие допущения. Толщина образца много меньше всех остальных размеров, поэтому образец будем рассматривать как бесконечно протяженный плоский слой. Материал и жидкость будем считать несжимаемыми средами. Распределение растворителя в слое считаем симметричным относительно продольной плоскости, которая проходит через центр образца и не зависит от продольных координат. Общее количество растворителя и его распределение в образце в процессе деформирования не меняются.

В качестве отсчетного выберем механически ненагруженное состояние образца с однородным распределением растворителя. В центр образца поместим декартовы координаты x_k и свяжем их с упругой матрицей. Ось x₁ направим поперек слоя, а оси x₂ , x₃ – вдоль (рис.1, б). Эти координаты будем рассматривать в качестве материальных.

Пространственное положение частиц полимерной матрицы в отсчетной конфигурации и в деформированном состоянии определим радиус-векторами следующего вида:

r = £ xkek , R = £ ^X_kek , Xi = X₁⁽xi ) , X2 = ^X2X2, Xз = X₃x₃,                 (10)

k=1                  k=1

где e_k – ортонормированный декартов базис; X_k – пространственные декартовы координаты, определяющие положение частиц полимерной матрицы в деформированном состоянии; X2, X₃ - константы, характеризующие относительное удлинение слоя в продольных направлениях.

Из соотношений (10) находим градиент деформации и его третий инвариант:

„         3                     3

F = V R = £ Xде,, B = £ X2ee, B = £ X2e, e, ,(11)

г=1                      i=1

где B – мера деформации Фингера.

J = X1X2X3, X, = X,/j1/3 , X1(X1) = X‘(X1).(12)

Из первого равенства (12) получим, что поперечное удлинение слоя

X1 (x, ) = J (x,) / (X 2X3).

Поскольку тензор напряжений Коши и мера Фингера соосны, то T = £ст_ke_ke_k , где c_k -k=1

главные компоненты тензора напряжений Коши, которые в силу (12) зависят только от поперечной координаты x1 . Тогда уравнение механического равновесия и граничные условия, задающие нагружение слоя, будут иметь вид [6]

5о1 / 5х1 = 0, о1 = 0 при х1 = ±h , /о^ \ = 0, P = /о°

где 2h - толщина образца в отсчетном состоянии; о0 = JX-оk - компоненты тензора напряжений Пиолы; угловыми скобками обозначена операция интегрирования вида

(4 =( 2 h Г¹ С

dx1 ; P – это средняя сила, действующая на единицу площади поперечного сечения слоя в отсчетном состоянии. Она характеризует упругую реакцию образца.

Распределение растворителя в образце зададим симметричной функцией

J = J(х1), J(-х1) = J(х1), |xj < h .

Это условие позволяет полагать, что неоднородно набухший слой останется плоским.

Второе и третье условие в (14) означает, что вдоль осей x1 , x2 слой механическому нагружению не подвергается.

Для применения общей теории решения данной задачи необходимо иметь конкретный вид определяющего соотношения (8). Для этого обратимся к теории полимерных сеток Флори–Ренера [7]. Система «полимер – растворитель» в ней рассматривается как изотропная, несжимаемая и аддитивная смесь. Плотность свободной энергии согласно этой теории имеет вид f = RT(n, Inф1 + XП1Ф2 + 2n2Ф22/3A),   A = 11(B) = 11J2/3 , B = B/J2/3 .(15)

Здесь T – абсолютная температура; R – универсальная газовая постоянная; χ – параметр Флори – Хаггинса, I₁ – первый инвариант меры деформации Фингера.

С учетом (8) и (15) тензор напряжений Коши

T = RTVЛ|г 3(B - 3I1E) - pE,                    (16)

где V₂ – мольный объём цепей полимерной сетки.

Используя соотношения (11) и (16) , находим оk = RTV^Й -111) - p, при k = 1, 2, 3.                  (17)

Из первых двух соотношений (14) получаем, что σ1 равно нулю. Отсюда, с помощью соотношения (17) для о1, выразим гидростатическое давление p и подставим его в выражения для о. и о3. Далее, учитывая второе равенство (12), условие несжимаемости и соотношение (13), получим ok = JXк1ак = G (Xk - J2X22X32Xk1),     при k = 2, 3,              (18)

-1м0\И где G = RTV2 (Ф2 )/3 - модуль сдвига материала в отсчетном состоянии. Из третьего уравнения (14) и соотношения (18) получаем X4 = JJ2^ X-2. Отсюда и из четвертого выражения (14) находим упругую реакцию слоя

P = G (x₃-X₃²J²)^1/2).                                  (19)

Это равенство отличается от известной классической формулы наличием во втором 2 1/2

слагаемом множителя J 2   , который учитывает неоднородность распределения растворителя.

Неоднородно набухшее состояние материала в данном случае не является термодинамически равновесным. Поэтому с течением времени растворитель равномерно распределится в объеме материала и согласно выражению (19) в конечном состоянии его равновесная реакция будет иметь вид P = G (13 -132 J0), где J0 -отношение объемов материала в конечном и отсчетном состояниях. В качестве отсчетного выберем состояние, относительно которого J₀= Jj^ = 1. Тогда реакция однородно набухшего образца будет описываться классической формулой

P = G (13 -1-2) .                                     (20)

Сравним (20) с величиной реакции неоднородно набухшего образца (19). Функцию J(x) представим в виде J = 1 + 0(x). В силу выбора отсчетного состояния 1

(0^ = 0, поэтому (J²у = 1 + (0 / и P = G[13 -1-2 (1 + (0² И ²]. Отсюда видно, что

P - P = G1-2

1/2

(1 + (0²}) -1

>0.

Таким образом, согласно классической теории высокоэластичности упругая реакция неоднородно набухшего плоского образца в условиях одноосного растяжения меньше его реакции в состоянии однородного распределения растворителя (при неизменном количестве растворенной в образце жидкости). В однородном состоянии упругая реакция образца максимальна.

Если слой внешнему механическому нагружению не подвергается, тогда

12 =13 (ст0) = (°0) = 0 ^0 = ^0 = g(13 -J21-5).

Отсюда получаем

1₂=13 = J2у6 =(1 + (0²⁶> 1.                        (22)

Из (22) следует, что по мере выравнивания концентрации растворителя в слое его продольные деформации уменьшаются.

а                                      б

Рис.2. Распределение продольных напряжений ^2 (б) в неоднородно набухшем образце, при заданных распределениях растворителя (а): кривые 1, 2, 3 соответствуют неоднородным состояниям, 4 – однородному распределению

На рис.2 представлены результаты расчёта продольных напряжений (в безразмерном виде) неоднородно набухшего слоя при различных распределениях растворителя в образце. Зависимость упругой реакции от характерного удлинения показана на рис.3. Кривые 1–3 соответствуют различным распределениям растворителя, которые представлены на рис.2, а.

Рис.3. Зависимость упругой реакции от характерного удлинения

Заключение

В данной работе из вариационного принципа, сформулированного на основе законов классической термодинамики, получена общая система уравнений, описывающих напряжённо-деформированное состояние сетчатых полимеров с неоднородным распределением растворителя. Показано, что полученная система уравнений аналогична известной статической задаче теории упругости для несжимаемого материала и в случае однородного распределения растворителя они полностью совпадают.

В рамках модельной задачи рассмотрено деформационное поведение эластомеров и полимерных гелей с неоднородным распределением растворителя. Получено решение задачи об одноосном растяжении неоднородно набухшего плоского слоя полимерного геля с симметричным распределением растворителя. Используя модель полимерных сеток Флори – Ренера, получены неравенства, которые позволяют сравнивать упругую реакцию и деформированное состояние плоских образцов с однородным и неоднородным распределением растворителя. Такие неравенства можно проверить экспериментально в опытах с нелетучими жидкостями. Результаты такой проверки могут быть использованы для оценки адекватности различных моделей полимерных сеток и теорий высокоэластичности.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований и администрации Пермского края (коды проектов РФФИ 08-08-00541 и РФФИ – Урал 07-01-96017); гранта Президента РФ (НШ-3717.2008.1).