Упруго-пластическое кручение двухслойного стержня

Статья продолжает серию работ посвященных использованию законов сохранения для решения краевых задач уравнений механики деформируемого твердого тела. Уравнения упругости и пластичности уже достаточно давно изучаются с помощью симметрий [1; 2]. Далее было показано, законы сохранения можно использовать и они были использованы для решения краевых задач для двумерных уравнений пластичности [3 – 12]. Эти работы показали, что законы сохранения более хорошо подходят для решения краевых задач, чем точечные симметрии, на которые ранее делалась ставка [2]. Это объясняется тем, что симметрии по своей природе являются локальными, в отличие от законов сохранения – глобальными по своей сути. Далее законы сохранения были применены для решения упруго-пластических задач о кручении стержней и изгибе консолей, а также решению упруго-пластических задач для пластин конечных размеров, ослабленных отверстиями [13 – 18]. В настоящей работе показано, что законы сохранения можно использовать и для решения краевых задач для многослойных материалов.

Постановка задачи

Рассмотрим прямолинейный стержень, поперечное сечение которого изображено на рис. 1. Пусть S ₁ и S ₂ области, занятые упруго-пластическими изотропными материалами, у которых предел текучести при чистом сдвиге одинаковый и равен k , а упругие постоянные Ламе различны и равны λ ₁, µ ₁ и λ ₂, µ ₂ соответственно. Пусть линия раздела материалов прямолинейна. Выберем ось координат ОХ вдоль линии раздела. Предполагается, как обычно, что боковая поверхность стержня свободна от напряжений, а стержень скручивается парой сил с моментом

M = ∫∫ ( y σ ₁₃ - x σ ₂₃) dxdy .

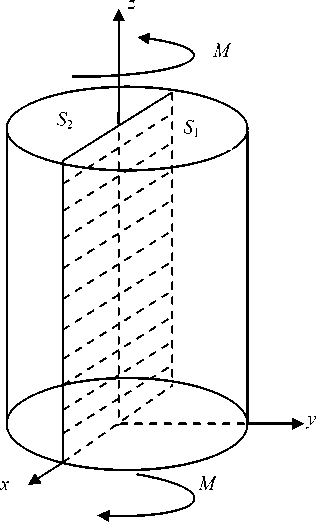
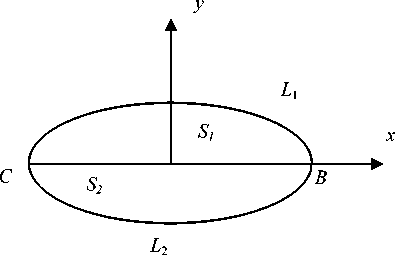
Рис. 1. Кручение двухслойного стержня

Fig. 1. Twisting of a two-layer rod

В этом случае уравнения, описывающие напряженное состояние в области S i i = 1,2 имеют вид

F ₁ =∂ x σ ₁₃ +∂ y σ ₂₃ = 0, F ₂ =∂ y σ ₁₃ -∂ x σ ₂₃ +µ i ω= 0, µ i ω= Ki ,               (1)

где σ13 , σ23 – компоненты тензора напряжений, ω – угол закручивания, он предполагается по- стоянным.

На боковой поверхности стержня выполняются условия σ ₁₃ n ₁ + σ ₂₃ n ₂ = 0, σ ₁₃ +σ ₂₃ = k ,

которые означают, что боковая поверхность свободна от напряжений и находится в пластическом состоянии.

Из (2) получаем

σ ₁₃ = kn ₁, σ ₂₃ = - kn ₂ .                                         (3)

Также предполагаем, что на линии раздела CD компоненты тензора напряжений непрерывны, это означает отсутствие разрыва напряжений для данного стержня вдоль CD .

Законы сохранения

Закон сохранения ищем в виде

Ax + By =ρ 1 F 1 +ρ 2 F 2 ,                                   (4)

где ρ ₁, ρ ₂ – некоторые функции, одновременно тождественно не равные нулю, буквенные индексы внизу означают производные по соответствующим переменным.

Замечание. Более подробную информацию о законах сохранения, их вычисления и использования можно найти в цитированной выше литературе.

Пусть

A=α1u+α2v+α3, B= β1u+β2v+β3,(5)

где для удобства положили σ ₁₃ = u , σ ₂₃ = v , α ¹, α ², α ³, β ¹, β ², β ³ – предполагаются функциями только x , y .

Подставляя (5) в (4) получаем 122112   12   33  2

α=β , α=-β , α _x -α _y = 0, α _y +α _x = 0, α _x +β _y =-α K_i ,

Пусть

α1x(i) - α2y(i) =0, α1y(i) + α2x(i) =0, α3x(i0+β3y(i0=-α2Ki,i=1,2

Здесь индекс i в скобках соответствует области S i .

Предположим, что в точке x ₀, y ₀подынтегральные функции имеют особенность и эта точка находится в круге радиуса ε :( x - x ₀)² + ( y - y ₀)² =ε ² (рис. 2), тогда из (4) получаем ∫∫ ( Ax + By ) dxdy = ∫∫ ( A ¹ x + B ¹ y ) dxdy + ∫∫ ( A ² x + B ² y ) dxdy = - ∫ A ¹ dy - B ¹ dx + S                          S ₁                          S ₂                             ε

+ ∫ A ¹ dy - B ¹ dx + ∫ A ² dy - B ² dx + ∫ A ¹ dy - B ¹ dx + ∫ A ² dy - B ² dx = 0 L ₁                L ₂                CD               DC

Имеем вдоль CD

∫ A ¹ dy - B ¹ dx + ∫ A ² dy - B ² dx = ∫ ( α ¹⁽¹⁾ u + α ²⁽¹⁾ v + α ³⁽¹⁾) dy - ( -α ²⁽¹⁾ u + α ¹⁽¹⁾ v + β ³⁽¹⁾) dx +

CD            DC             CD

+ ∫ ( α ¹⁽²⁾ u + α ²⁽²⁾ v + α ³⁽²⁾) dy - ( -α ²⁽²⁾ u + α ¹⁽²⁾ v + β ³⁽²⁾) dx = 0

DC

L 1

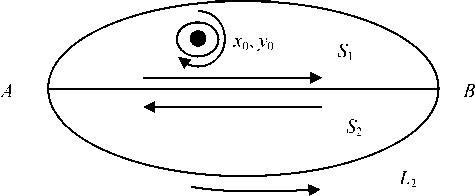
Рис. 2. Схема взятия интегралов по поперечному сечению

Fig. 2. The scheme of taking integrals over the cross section

Поскольку вдоль CD dy = 0, то полагаем Р 3( i ) = 0, а | ( i ) = а ² ( i ) Ki , поэтому а ¹⁽¹⁾ = а ¹⁽²⁾, а ² ( ¹⁾ = а ² ( ²⁾.

В результате получаем

J A ¹ dy - B ¹ dx = J A ¹ dy - B ¹ dx + J A ² dy - B ² dx .                       (8)

£                      L y                      L 2

Воспользуемся формулой (8) для нахождения функций u , v в точке Для этого рассмотрим решение уравнений (7) в виде

а

x - Xo           2

---------2----⁰-------2, “

⁽ x ^- x 0 ) + ^{( y - y} 0 )

y - Уо           з x - xo

--------2---⁰------2 , а = OHM irclg----- -. ⁽ x ^- x 0 ) + ^{( y - y} 0 )                  ^{y - y} 0

Подставляя (9) в (8) получаем

J A ¹ dy - B ¹ dx = J ( а ¹ u + а ² v + а ³) dy - ( -а ² u + а ¹ v ) dx =

£                       £ x - x0

V ^{( x - x} 0 ^{)2 + ( y - y} 0 ⁾²

У ^- У 0

^{( x - x} 0 ⁾² + ^{( y - y} 0 ⁾²

x - xn v + wp.1arctg------

У ^- У 0 J

dy

-

__yy__

V ^{( x - x} 0 ⁾² + ⁽ y ^- y 0 ⁾²

u dx +

J

Г          x - X n        ,             У — У п        ,                x = X n

+ I --------,--- 0------- , kn +--------,----0------у kn 2 + mu 2arctg-----0

L ₂ 1 ^{( x - x} 0 ) 2 ^{+ (} У ^- У 0 ) 2       ^{( x - x} 0 ) 2 ^{+ (} У ^- У a )                 У ^- У 0 J

dy -

y2y02kn1

(x - x 0) + (y - y 0)

x - x_n

-------2------m kn 2

(x - x0) +( y - y 0) J

dx .

Рассмотрим решение уравнений (7) в виде a1 =------^2-^0-----2, a2 = ------X0------2, a3 =1 m^lntXx-xq)2 +(y-yq)2).

^{( x - x} o ) + ^{( y - y} o )         ^{( x - x} o ) + ^{( y - y} o )         ²

Подставляем (11) в (8) получаем

^{2 n}^ 23 ^{( x} 0 , У 0 ) =

J (---- P⁰ ----Г kn i

L ^{( x} - ^x 0 )² + ⁽ y ^- y 0 )²

x - x0        ,

⁰ kn ₂

^{( x - x} 0 )^{2 + (} y ^- y 0 )²

2 to^ 2 ^{ln(( x - x} 0 )^{2 + (} У ^- У 0 ⁾²⁾ dy ^-

+ J £

vdx

J

x - x ₀

V ⁽ x ^- x 0 ^{)2 + (} y ^- y 0 ⁾²

kn 1 +

y ^- y 0

^{( x - x} 0 ^{)2 + ( y - y} 0 ⁾²

kn ₂ + top. 1 arctg

x-x ° dy у ^- у 0 J

----^y 0 ----2 kn 1

V ^{( x - x} 0 ) ^{+ ( y - y} 0 )

x - x ₀

^{( x - x} 0 ⁾² + ^{( y - y} 0 ⁾²

kn ₂ dx +

- ( ^x—^x -----у kn +----- y—y ⁰----- у kn ₂) dx +

(x - xq)2 + (y - yq)2      (x - xq)2 + (y - yq)2                              (12)

+ J (yP0----2kni + x - xa

^{( x - x} q^{) 2} + ⁽ y ^- y q^{) 2}

kn 2 ⁺ 2 ®^ 2 ^{ln(( x - x} a )^{2 + (} У ^- У q^{) 2 )} dy-

L ₂   ^{( x - x} a ) ^{+ (} У ^- У a )

-(--^j—x-----2 kn1 +------y2—y0-----2 kn 2 ) dx.

^{( x - x} q^{) 2} + ⁽ y ^- y q^{) 2      ( x - x} q^{) 2} + ⁽ y ^- y q^{) 2}

Заключение

Формулы (10), (12) позволяют вычислить значения компонент тензора напряжений во всех точках поперечного сечения. Далее в каждой точке x ₀, y ₀ проверяется условие пластичности G 2 ₃ +G 2 ₃ = k ². Те точки, где a 2 ₃ + G 2 ₃ <  k ². принадлежат упругой зоне, а остальные точки -пластической области. Тем самым описанная процедура позволяет выделить пластические и упругие зоны и построить упруго-пластическую границу, которая заранее была неизвестна и подлежала определению.