Упруго-пластическое самоупрочнение (автофретирование) толстостенных контейнеров давлением эластичной среды

• ¹    Самарский государственный аэрокосмический университет

• ²    Государственный научно-производственный ракетно-космический центр «ЦСКБ-Прогресс», г. Самара

Исследованы технологические возможности упрочнения цилиндрических контейнеров автофретированием с использованием давления эластичной среды. Разработана методика расчетов основных параметров процесса упрочнения автофретированием с учетом особенностей деформирования и сжимаемости эластичной среды (полиуретана). Получено выражение для определения модуля объемного сжатия различных марок и твердостей полиуретана.

Авторами разработан способ упрочнения круглых контейнеров автофретированием с применением высокого давления полиуретана [1] взамен традиционных методов (дорнование, гидростатирование и др.). Полиуретан, являясь рабочим телом в контейнерах ддя штамповки, также может быть эффективно использован в качестве рабочего тела при автофретировании.

Для исследования технологических возможностей автофретирования контейнеров давлением эластичной среды проведен теоретический анализ данного эффективного процесса упрочнения.

За основу в теоретическом анализе процесса автофретирования контейнеров принят метод Девидсона-Кендалла [2]. Метод базируется на следующих допущениях:

• 1.    Так как упругие и пластические деформации являются величинами одного порядка, принимается модель упругого идеально-пластического материала, т.е. материал контейнера сжимаем упруго во всей области и сохраняет объемные изменения, вызванные упругими напряжениями. Кроме того, в области малых пластических деформаций материал контейнера обладает низким деформационным упрочнением.

• 2.    Распределение продольных напряжений и деформаций по толщине стенки контейнера принимается постоянным.

• 3.    Применяется условие текучести Треска (условие постоянства максимальных напряжений сдвига)

O - O r = O s . ⁽¹⁾

Известно [3], что зависимость упругих напря

жений в толстостенном цилиндре от внутреннего давления определяется уравнениями Ляме

Ot

Or

qt к2 -1

(

1 +

V

^rl 1

qt k2 -1

(

1 -

V

r 1

Для упруго-пластичного цилиндра (при автофретировании) напряжения в упругой зоне можно получить из уравнений (2) и (3) с учетом того обстоятельства, что радиальное напряжение на границе упругой и пластичной зон (при r =р ) равно давлению начала пластического течения

q y = о

k ²

-

2 k ²

Отсюда следует ор 2

^O re = j

2 r ²

(

V

-

r l

,

O

te

^O s P ² 2 r 2 ²

( 1

V

+ r 1 7

.

Напряжения в пластической зоне определяются из совместного решения условия текучести (1) и уравнения равновесия

^O t ^- O ^{- r} ,' = 0 . dr

Интегрируя полученное в результате дифференцированное уравнение

J d^O r = O J ¹ dr (8)

и используя граничные условия:

при

r = ro = - qi r = pO = o

^p — 2 k ² In ^p = 2 — k' r ₁²              r ₁             ^.

получим выражения для радиальных ^o r _p

и тангенциальных O _t p напряжений в ческой зоне

пласти-

(

P

O = ^—O , lg r ⁺

\

O = O lp           s

lg ^P + r

2    _ 2 \

^

2 r J'

2 . „2\ r2 + p

2r ²

2r2 J

,

•

Следовательно, внутреннее давление, которое вызывает пластическое течение материала контейнера до радиуса р , равно

(1 p   r^г qi=—O , ^lg 7 + -

-

p ² 1

1г

^2r2   ⁷

•

Контейнер может быть автофретирован так, что величина остаточных напряжений вызывает на его внутренней поверхности вторичные пластические деформации обратного знака (Эффект Баушингера). Во избежание этого явления необходимо ограничивать автофре-тирующее давление до значения, обеспечивающего остаточное напряжение не более величины предела текучести (100% автофретирование). При этом условии контейнер разгружается упруго. Тогда величина остаточных напряжений равна разности между напряжениями от давления автофретирования для упруго-пластического случая и напряжениями от того же давления, вычисляемыми по формулам Ляме (2), (3). Это условие для тангенциальных напряжений можно записать как:

O_t — O, = — о , l p            l e               ^s 7

после подстановки получим

'

O

V

1 P г2 lg-+~ r1

p ^{2 1}

2 r ²

²   7

O s lg ^p + ~

—

L2L k ²

p ^{2 4}

2 r 2²

( г² 1

^J- 1+    = ^os

s

I r J

Уравнение (14) можно преобразовать к более удобному выражению для определения значения р , характеризующего границу раздела пластической и упругой областей автофрети-рованного на 100% контейнера

Таким образом, зная величину р , по уравнению (12) вычисляется необходимое давление для 100% автофретирования контейнера.

Для того, чтобы определить допустимое давление q A при повторных нагружениях контейнера, необходимо исходить из условия его работы в упругом режиме. В этом случае напряженное состояние на внутренней поверхности описывается как:

^о t = ^{о + о} t_OCT ,           ⁽¹⁶⁾

о = ^— q A .            ⁽¹⁷⁾

где o q - тангенциальное напряжение на внутренней поверхности контейнера, вычисленное по формуле Ляме (2) от приложения

давления q A ; о _tOC _T - тангенциальные остаточные напряжения при 100% автофретировании,

т.е. о, = —о,. lOCT

Используя условие текучести Трески (1), уравнение (16) можно записать в виде:

k ² +1

qA    г—о = — qA+ о,(18)

k — 1

k ² —1

qA=os k- ■

Нетрудно показать, что выражения (12) с подстановкой условия (15) 100% автофретирования и (19) равнозначны. Выражение в круглых скобках в формуле (12) можно преобразовать к виду:

25 ⁽

\

2 k ² lg ^p — ^Z + k² r 1      r 1²

или с учетом условия (15)

2^ [ — ( 2 — k ²) + k ² ] =       ,

т.е. допустимым давлением повторного нагружения контейнера, при котором последний будет работать упруго, является автофре-тирующее давление.

Применяя аналогичный подход, можно получить выражения для определения р и q. при любом случае автофретирования (90%, 80% и т.д.). Для этого условие (13) записывается как

O p — ^O t e =^{— B O} S ,        (22)

где В - коэффициент, отражающий долю остаточного напряжения от 100% автофретирования.

В этом случае радиус границы раздела пластической и упругой областей может быть определен по формуле:

7^- k ln^T = B (1 — k ⁾⁺¹ , (23) r ₁             r ₁

автофретирующее давление, соответ ственно, выражается уравнением q, = о

( B +*² -1 ¹

2 k ²

Формулы (19) и (24) определяют автофретирующее и максимальное рабочее давление при условии воздействия нагрузки по всей высоте контейнера. В реальных условиях высота полиуретанового блока заведомо меньше высоты контейнера, что обусловлено необходимостью захода сжимающего инструмента. Кроме того, известно [4], что в замкнутом объеме при высоком давлении происходит сжатие полиуретана. Для уточнения формул (19) и (24)

предположим, что давление сжатия q¹^ полиуретана при осуществлении процесса автофретирования (или при рабочем нагружении) превосходит расчетное q A (или q_t ) в величину отношения высоты контейнера Н_к к высоте полиуретановой подушки H ny в момент сжатия, т.е.

qa

1 сж

qi

H k

H n / у ’

или выражая через начальную высоту полиуретанового блока Hny и относительную деформацию полиуретана по высоте £„ / у , можно написать qa с^ж

qiH K

^ п / у ^{) Н} п / у 0

С другой стороны, пренебрегая сжатием полиуретана за счет изменения внутреннего диаметра контейнера, еп / у

qa

1 сж

E v ’

где E v - модуль объемного сжатия полиуретана.

Подставив выражение (27) в формулу (26), получим

^E v ^-

a q сж

I Г

^E v ^E v ^{- 4} q , k

H ) н, n / У о )

.

Поскольку для расчета силовых параметров процесса автофретирования контейнеров необходимо знание модуля объемного сжатия полиуретана Ev , данные о котором отсутствуют в справочной литературе, были проведены дополнительные эксперименты по определению сжимаемости полиуретана различных марок и твердостей в замкнутом объеме [5]. Сжатие полиуретановых блоков производилось с обоих сторон пуансонами, входящими в контейнер по скользящей посадке. Испытание полиуретана на сжимаемость осуществлялось на разрывной машине марки ГСМ-50 с записью диаграммы “усилие-перемещение”. В экспериментах применялся полиуретан марок СКУ7Л твердостью от 80 до 98 ед. по Шору А, получаемый с предприятия-изготовителя за последние 5 лет. Изготавливалось по 5 образцов каждой марки и группы твердости в пределах отклонения не более 2 ед. Шора А, т.е. 80-82,83-85,8688 ед. Шора А. Следует также отметить, что во избежание влияния гистерезисных потерь на показатели сжимаемости производилось пятикратное нагружение образцов до максимального давления 500 МПа без записи диаграммы и трехкратное нагружение до данного давления с записью диаграммы “усилие-перемещение”. После расшифровки диаграмм была произведена их перестройка в координатах £ _v и q, Ev и q , т.е. относительной сжимаемости и модуля объемного сжатия полиуретана от приложенного давления. Полученные зависимости представлены на рис.1 и 2.

С целью определения аналитического выражения модуля объемного сжатия E v была произведена аппроксимация представленных зависимостей.

В результате обработки экспериментальных данных выражение модуля объемного сжатия полиуретана представляется зависимостью

Е, = a - e b^ [ ( с + d - q „ T - 1 ] , (33)

где a, b, c и d - постоянные коэффициенты выражения Ev, T v - твердость полиуретана.

После проведения расчета параметров процесса 100% автофретирования ( q . , q _сж , р, Ev ) текущих и остаточных тангенциальных дефор-

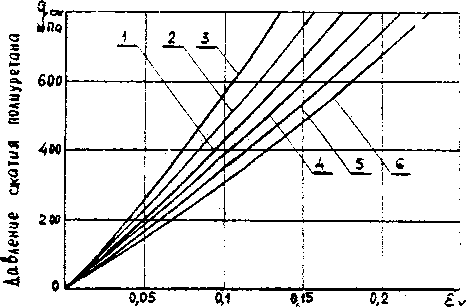
Относительное изменение объема

Рис.1. Диаграммы сжимаемости полиуретана: 1, 2, 3 - твердость 88-86, 85-83, 82-80 ед. Шора А, марка СКУ7Л; 4, 5, 6 - твердость 98-96, 95-93, 92-90 ед Шора А, марка СКУПФЛ и L-1000.

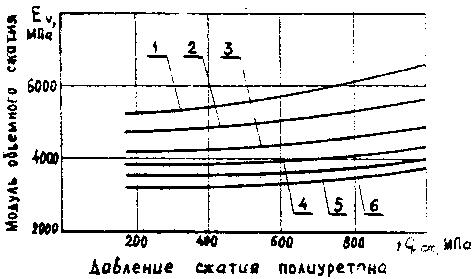
Рис.2. Изменение модуля объемного сжатия полиуретана в зависимости от величины гидростатического давления: 1, 2, 3 - твердость 88-86, 85-83, 82-80 ед. Шора А, марка СКУ7Л; 4, 5, 6 - твердость 98-96, 95-93, 92-90 ед. Шора А, марка СКУПФЛ и L-1000.

маций автофретирования контейнеров с заданным относительным размером k = r 2 / r 1 был реализован реальный процесс автофретирования с экспериментальным замером текущих и остаточных тангенциальных деформаций. Сравнение результатов по значениям тангенциальных деформаций показало удовлетворительную сходимость расчетных и экспериментальных данных.

С целью проверки работоспособности ав-тофретированных на 100 % контейнеров в упругом режиме производилось многократное их нагружение рабочим давлением, равным авто-фретирующему. Остаточные деформации в контейнерах при этом не изменились.

На основании положительных результатов проведенных исследований можно отметить пригодность разработанного способы упрочнения и принятого метода расчета в определении основных параметров процесса автофретирования контейнеров полиуретаном.

Способ упрочнения автофретированием контейнеров для штамповки деталей полиуре- таном внедрен в заготовительно-штамповочном производстве ряда предприятий аэрокосмической отрасли.