Упругодиффузионные колебания изотропной пластины Кирхгофа-Лява под действием нестационарной распределенной поперечной нагрузки
Автор: Гу Юй, Земсков А.В., Тарлаковский Д.В.
Статья в выпуске: 3, 2021 года.
Бесплатный доступ
Исследуются нестационарные упругодиффузионные колебания свободно опертой прямоугольной изотропной пластины Кирхгофа-Лява, находящейся под действием распределенной поперечной нагрузки. Для математической постановки задачи используется модель, описывающая связанные упругодиффузионные процессы в сплошных многокомпонентных средах с учетом релаксации диффузионных потоков. Из нее с помощью вариационного принципа Даламбера получены уравнения поперечных колебаний прямоугольной изотропной пластины Кирхгофа-Лява с учетом диффузии. На основе полученных уравнений сформулирована постановка начально-краевой задачи об изгибе свободно опертой изотропной прямоугольной пластины под действием распределенных по поверхности упругодиффузионных возмущений. Решение задачи о нестационарных упругодиффузионных колебаниях пластины ищется в интегральной форме. Ядрами интегральных представлений являются поверхностные функции Грина, для нахождения которых используется преобразование Лапласа по времени и разложение в двойные тригонометрические ряды Фурье по пространственным координатам. Трансформанты Лапласа функций Грина представлены через рациональные функции параметра преобразования Лапласа. Переход в пространство оригиналов осуществляется аналитически с помощью вычетов и таблиц операционного исчисления. Получены аналитические выражения для поверхностных функций Грина рассматриваемой задачи. В качестве расчетного примера рассмотрен изгиб свободно опертой механодиффузионной пластины, находящейся под действием внезапно приложенных, распределенных по поверхности нестационарных изгибающих моментов. На примере трехкомпонентного материала выполнено численное исследование взаимодействия нестационарных механического и диффузионного полей в изотропной пластине. Исследовано влияние релаксационных эффектов на кинетику массопереноса. Решение представлено в аналитической форме и в виде графиков зависимости искомых полей перемещения и приращений концентрации компонент среды от времени и координат. В заключение приведены основные выводы о влиянии связанности полей и релаксационных эффектов на напряженно-деформированное состояние и массоперенос в пластине.
Упругая диффузия, преобразование лапласа, ряды фурье, функции грина, пластина кирхгофа-лява, нестационарные задачи
Короткий адрес: https://sciup.org/146282367
IDR: 146282367 | УДК: 539.3, | DOI: 10.15593/perm.mech/2021.3.05
Текст научной статьи Упругодиффузионные колебания изотропной пластины Кирхгофа-Лява под действием нестационарной распределенной поперечной нагрузки
ВЕСТНИК ПНИПУ. МЕХАНИКА № 3, 2021PNRPU MECHANICS BULLETIN
We investigated an unsteady elastic diffusion vibration of a simply supported rectangular isotropic Kirchhoff-Love plate. The plate is under the action of a distributed transverse load. A model that describes coupled elastic diffusion processes in a multicomponent continuum is used for the mathematical problem formulation. The model is taking into account the diffusion fluxes relaxation. The transverse vibration equations of a rectangular isotropic Kirchhoff-Love plate with diffusion were obtained from the model using the d'Alembert variational principle. The initial-boundary value problem of a freely supported isotropic rectangular plate bending is formulated on the basis of the obtained equations. The plate is under the action of elastic diffusion perturbations distributed over the surface.
The problem solution of an unsteady elastic diffusion plate vibration is sought in an integral form. The surface Green's functions are the kernels of the integral representations. To find the Green's functions, we used the Laplace transform in time and the expansion into double trigonometric Fourier series in spatial coordinates. Green's functions in the image domain are represented in the form of rational functions and depend on the Laplace transform parameter. The transition to the original domain is done analytically through residues and tables of operational calculus. The surface Green's function analytical expressions are obtained.
As a calculation example, we considered a freely supported elastodiffusive plate under the action of suddenly applied unsteady bending moments distributed over the plate surface. By using a three-component continuum, a numerical study of interactions between unsteady mechanical and diffusion fieldsis done for an isotropic plate. The influence of relaxation effects on the kinetics of mass transfer is investigated. The solution is presented in the analytical form, as well as in the graphs of the displacement fields and concentration increments on time and coordinates.
At the end of the publication, the main conclusions are given about the fields coupling effect and the relaxation of diffusion fluxes on the stress-strain state and mass transfer in the plate.
В настоящее время существует большое количество работ, посвященных изучению механодиффузионных эффектов в сплошных средах. Экспериментальные исследования этой проблемы были начаты в 30-х годах ХХ века. Было показано, что в результате изгиба пластинки из сплава золота и меди градиент деформации инициировал процесс восходящей диффузии. Это привело к формированию градиента концентрации и, как следствие, перераспределению атомов растворенного вещества. В результате возник перенос вещества из областей сжатия в области растяжения. Результат научных исследований был опубликован в 1936 году [1].
Дальнейшие эксперименты позволили установить, что упругие деформации сжатия лишь немного уменьшают коэффициент самодиффузии в некоторых металлах [2, 3]. Это позволяет сделать вывод о том, что упругая деформация слабо влияет на диффузию и основные механодиффузионные эффекты наблюдаются только в области пластической деформации.
Первые модели, описывающие указанные явления, появились в 60-х годах ХХ века. В настоящее время в рамках феноменологического подхода наибольшее развитие получили модели, основанные на теории гомогенных смесей, где компоненты, их составляющие, переме- шаны и взаимодействуют на молекулярном или атомарном уровнях (поверхности раздела частей отсутствуют). К ним относят твердые тела с примесями, сплавы, твердые растворы (однофазные кристаллические или аморфные твердые вещества переменного состава из двух или более компонентов). Такой подход обладает рядом преимуществ, основным из которых является то, что физические свойства гомогенных смесей во всех частях одинаковы или меняются непрерывно, без скачков, что позволяет эффективно применять аппарат дифференциального исчисления. Кроме того, с точки зрения термодинамики такие смеси представляют собой однородные термодинамические системы, каждой точке которых в условиях равновесия соответствуют одинаковые значения давления, температуры и концентрации, что тоже существенно упрощает процесс моделирования механодиф-фузионных явлений. Из наиболее свежих публикаций можно назвать [4–20]. Здесь рассматриваются различные постановки задач термомеханодиффузии, в том числе с конечной скоростью распространения тепловых и диффузионных потоков, а также предлагаются методы решений соответствующих стационарных и нестационарных задач.
Обзор публикаций по данной тематике показывает, что проблема анализа взаимодействия механического и диффузионных полей является актуальной. Наибольший практический интерес представляют задачи для балок, пластин и оболочек, которые составляют основу большинства конструкций. Среди немногочисленных публикаций по этой теме можно отметить статьи [21, 22]. В них исследуется влияние диффузионных процессов на несущую способность пологой трансверсально-изотропной оболочки. Контактное взаимодействие стержня с упругим полупространством рассматривается в работах [23, 24]. Публикации [25–27] посвящены исследованию механодиффузионных процессов в пластинах. Расчет сферических оболочек с учетом диффузии рассмотрен в [28].
Следует отметить, что все указанные задачи решаются в стационарной постановке. Постановки задач о нестационарных упругодиффузионных колебаниях балок и пластин и методы их решения в известных на сегодняшний день публикациях отсутствуют.
В данной статье исследуются эффекты взаимодействия механического и диффузионного полей в пластине Кирхгофа–Лява. Математическая модель упругодиффузионных колебаний пластины получена на основе вариационных принципов и известных соотношений теории пластин, изложенных в работах [29–32].
1. Постановка задачи
u,. = £2^ + f, n( q ^—JLl + Y (q), dXj 5x
n( N+1)=-£ n( q) ( q = 1Л), q=1
где оу и J ( q ) - компоненты тензора напряжений и вектора диффузионного потока, которые для идеального твердого раствора определяются следующим образом ( q = L N ) :
du
CT j = [ X8 y 8 ki + н ( 8Л 8 j +8 !7 6 jk ) ] --- 8 y £ a q n( q );
^x q=1
(q) ^2 (
J ( q > +T J ( q ) = -8 D ^3—+ Л 8.8w- d u- ' q 1 44 d xy q j J k 1 d x, d x
•
Здесь точки обозначают производные по времени. Все величины в (1) и (2) являются безразмерными. Для них приняты следующие обозначения:
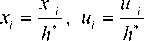
ct
T = 77, h ’
Рассматривается задача о нестационарных упругодиффузионных колебаниях прямоугольной изотропной пластины Кирхгофа–Лява с учетом релаксации диффузионных потоков. Схема приложенных сил и изгибающих моментов, а также ориентация осей прямоугольной декартовой системы координат представлена на рис. 1.
X ’ ц ’ c t( q )
---------, ц =---------, т =,
X ’ + 2 ц ’ X ’ + 2 ц ’
I *
/ = —, D„ =, m h ’ q ch ’
m ( q ) D ’( q ) a ’ ( q ) n ( q ) _ a ’ ( q )
pRToch’ ’ “q = X’+ 2ц’, p h * F * vW h * Y ’(q >
F =----- i —, Y (4) =------ ,
i
X + 2 ц c
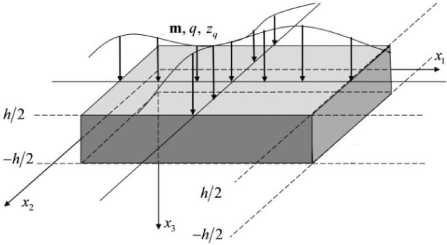
Рис. 1. Силы и моменты, действующие на пластину
X ’ + 2 ц ’ P
L h h h = — h *
= 1,
где t - время; x{ - прямоугольные декартовы коорди
Fig. 1. Forces and moments acting upon the plate
Здесь m = { m, m 2 } - распределённые по поверхности моменты; q – распределённая по поверхности поперечная нагрузка; zq – распределённые по поверхности плотности объемных источников массопереноса.
Для математической постановки задачи используется модель упругодиффузионных процессов в сплошных средах в прямоугольной декартовой системе координат, которая в случае однородной среды имеет вид [4–20, 33–35]
наты; u* - компоненты вектора перемещений; h’ толщина пластины; l и l – длина и ширина пласти-(q) (q)( ны; n = n — n( - приращение концентрации q-й компоненты вещества в составе многокомпонентной . (q) (q) __ среды; n и n – актуальная и начальная концентрации q-го вещества; X’ и ц’ - упругие постоянные Ламе; p - плотность; a’(q) - коэффициенты, характеризующие объёмное изменение среды за счёт диффузии; D’(q) - коэффициенты самодиффузии; R - универсальная газовая постоянная; Т0 - температура среды;
( q )
m – молярная масса q -го вещества; F – компоненты
( q )
вектора плотности массовых сил; Y – плотность источников массопереноса; т( q ) - время релаксации диффузионных потоков.
Полагаем, что поперечные прогибы пластины являются малыми. Считаем также, что прямолинейное нормальное к срединной поверхности волокно после деформации также остается прямолинейным и нормальным к срединной поверхности (пластина Кирхгофа–Лява). Линеаризуя перемещения по толщине пластины, получаем их (x, x2, x3, т) = u (x, x2, t) - x3
u 2 ( x , x2 , x 3, t ) = v ( x , x2 , t ) - x3
d w ( x , x 2, t ) d x
d w ( x , x 2, t ) d x2
u3 ( x , x2 , x3 , t ) = w ( x , x2 , t ) ;
n( q ) ( X 1 , X 2 , X 3 , t ) = N q ( X 1 , x 2 , т ) + X 3 H q ( x„X 2 , t ) . (4)
Далее, для построения уравнений изгиба пластины используется принцип Даламбера. В этом случае соотношения (1), (2) записываются в виде [29]
J u
G k
50 ij d Xj
- F S udG +
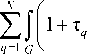
4#(" Х - /”1 5t J k d x ^
Sq q ) dG +
+ JJ ( ° i n j” P i ) S uidS +
N
+ Z JJ ( J iq ) + т q J q ’ - A q ) ^ q ) dS = 0. q = 1 n j
Здесь S u и 8ц( q ) — виртуальные перемещения и приращения концентраций; р , I ( q ) - поверхностные динамические возмущения. В соответствии с физической постановкой задачи полагаем, что р = 0 и 1г ' q ) = 0 .
Подставляя равенства (2) и (4) в вариационное уравнение (5), по аналогии с методикой, изложенной в работе [29], получаем уравнения упругодиффузионных поперечных колебаний пластины Кирхгофа–Лява с учетом релаксации диффузионных потоков ( А - оператор Лапласа)
N
Аw-12w = ААw +ZaqAHq -12(divm + q);
q = 1
mt = I x3Fdx3 ( i = 1,2 ) ;
- 12 (6)
H q +T q H q = D q A H q + Л q AA w + 12 Zq ;
Zq = J / ( q ) x3dx 3.
- 12
Математическая модель задачи о нестационарном изгибе свободно опертой пластины под действием распределенной нагрузки описывается уравнениями (6), которые дополняются нулевыми начальными условия- ми и граничными условиями, которые также получаются из вариационного уравнения (5) [29]:
|
( d 2 w _ d 2 w —T + ^— t + k d x 12 d x 2 |
:Z a , H ,' q = 1 J |
X 1 = 0 |
= 0; |
||
|
Г d 2 w . d 2 w —Г + ^~r + k d xx d x2 Г. d 2 w d 2 w ^—r + —r + k d x2 d x f |
IE « . ,H,' q = 1 J NL A Z a qHq q = 1 J |
X 1 = l 1 x 2 = 0 |
= 0; = 0; |
(7) |
|
|
. d 2 w d 2 w ■ X—- + —r + k d xx 2 d x 2 |
N A Z a q H q q = 1 J |
X 2 = 11 2 |
= 0; |
||
|
w x , =0 : |
= 0, w| , = 0, 1 x 1 = l 1 |
w l x 2 = 0 = |
0, |
w x 2 = 2 - |
0; (8) |
|
h I = 0, h I = 0, q l x j = 0 q l x 1 = 1 1 |
H l = q l x 2 = 0 |
0, |
H . l x , = 2 |
= 0. (9) |
|
2. Метод решения
Решения задачи о нестационарном изгибе пластины (6)-(9) под действием распределенных по поверхности возмущений F ( x , x 2, т ) = - 12 ( q + div m ) и
Fq+ т ( x , x 2, т ) = 12 z ( q ) представляем в виде ( q = 1, N + 1)
w ( x , x 2, t ) =
N + 1 т l1 l 2
= Z J J J G 1 k ( X 1 , X 2 , Z , Z , т - t ) F k ( Z , Z , t ) d Z d Z dt ;
k = 1000
Hq ( X 1 , X 2 , t) =
N + 2 т l1 l 2
= Z J J J G q + 1, k ( X , X 2 , Z , Z , т - 1 ) F k ( z , z , t ) d Z d Z dt , (10) k = 10 0 0
где Gmk - поверхностные функции Грина, удовлетворяющие уравнениям
А G 1 k - 12 G 1 k =АА G 1 k +
N
+ Z«qАGq+1,k -§1 k8(X1 -Z)S(X2 -Z)5(t);
q = 1
G q + 1, k +T q G q + 1, k =
= D q A G q + ] , k +Л q M G k +S q + 1, k S ( X 1 -Z ) S ( X 2 -Z ) 5 ( t ) (11) и однородным граничным условиям
|
Г d 2 Gk x |
d 2 Gu |
N |
||
|
---T^ + X k d X j2 |
1 k d x 2 |
•+ Z q = 1 |
/ a qGq + 1, k ^ |
X 1 = 0 |
|
Г 5 2 Gk . |
d 2 Gk |
N |
A |
|
|
—T^ + X k d x ,2 |
1 k d x 2 |
+ Z q = 1 |
f a qGq + 1, k J |
x 1 = l 1 |
|
fx c^Gxk |
2 |
N |
A |
|
|
X+ k d x 2 |
1 k d x 2 |
+ Z q = 1 |
r a qGq + 1, k J |
x 2 = 0 |
X
G 1 J x = 0 = 0,
|
d 2 G 1 k । d 2 G 1 k d xxг d x 2 |
N ) -+Ea qGq + 1, k q = 1 J |
x 2 = l 2 |
|
G»^l = 0, |
G - k l, = 0 = °, |
G 1 k |
|
G . - ., - 11 = 0 = |
0 Gq -L1= l/ |
0; |
|
° . -L=0 = |
0, Gq -L. 2. 1 2 |
= 0. |
= 0;
I X 2 = l 2 = 0; ( 12 )
5 qp , V nm Л q a p П p ( V nm , s )
l 1 1 2 [ k q + 1 ( V nm , s ) Qq ( V nm , s )
где
sin H m Z sin X n Z ,
N
n ( V nm , s ) = П kj + 1 ( V nm , s ) ;
j = 1
N
П j ( V■ , s ) = П kr + 1 ( V nm , s ) ;
Для построения функций Грина применяем к задаче (11) и (12) преобразование Лапласа по времени. Затем домножаем каждое уравнение на Sin Xn. Sin Hmx2, Xn = nn /1, Hw = nm /12 и интегрируем в прямоугольнике D = [0, l ] * [0, l2 ]. Получаем k1 (V nm , s ) GLs (X n , Hm , Z, Z, s )--]Eaqv2nmGL+1,k (Xn,Hm,Z,Z,s) = q=1
= TTS 1 k Si n H m Z Si n X n Z ;
-Л q V nm G Ls ( X n , H m , Z , Z , s ) +
+ kq + 1 (V nm , s ) Gq + 1, k (X n , H m , Z ’ Z , s ) =
= JPS q + 1, k Sin H m Z Sin X n Z
l 1 l 2
P (Vnm , s) = k1 (Vnm , s WVnm , s) - V'nm ^E “j jj (Vnm , s ) i j=1
Qq ( V nm , s ) = k q + 1 ( V nm , s ) P ( V nm , s ) •
Оригиналы в (15) находим с помощью вычетов и таблиц операционного исчисления (штрих обозначает производную по параметру s ) [29, 36]:
G s ( X n , H m , Z , Z , T ) =
= 74- Sin H m Z Sin X n Z E A 1 k ) ( v nm , s l ( V nm ) ) exp ( s i ( v nm ) t ) ;
l 1 1 2 l = 1
G qs + 1,1 ( X n , H m , Z , Z , t ) =
2 N + 4
Sin H m Z Sin X n Z E A q + 1,1 ( V nm , s l ( V nm ) ) exP ( s l ( V nm ) T )
l = 1
G qs + 1, p + 1 ( X n , H m , Z , Z , t ) =
Здесь
k1 (Vnm , s) = s2 (V2m + 12) + V4m , kq+1 (Vnm , s) = s + Tqs2 + DqV™ , v2m = Xn + Hm. ,
+
= 7ySin Hm Z Sin Xn ZE
l 1 1 2 l = 1
exP ( x l ( V nm ) T ) kq + 1 ( V nm , X l ( V nm ) )
д 2 N + 4
— sin Hm Z Sin Xn Z E Aq+1, p+i ( к l? l=1
2 N + 4
l = 1
.V nm , s l ( V nm ) ) exp ( s l ( V nm ) T ) ; (17)
G^5 (X n , H m , Z , Z , s ) =
4 l 1 l 2 L
= / / J J G ik ( L , x 2 , Z , Z , s ) Sin X n x Sin h m x 2 dx 2 dx 1 ;
l 1 l 2 00
A n’ ( V nm , s l
G L ( x„X 2 , Z , Z ,s ) =
AM + 1 ( V nm , s l
, = n(V- , s (V- » ;
P '( V nm , s l ( V nm ) )
V 2 m a q П q ( V nm , s l ( V nm ) ) .
P ' ( V nm , s l
= EE G L ( X n , H m , Z , Z , s ) Si n X nX 1 Sin H mX2 •
A q + 1,1 ( V nm , s l
V 4 m Л q n ( v
Q i ( V nm , s l
nm , s l (V nm )).
—/---v\—; (18)
Решение системы (13) имеет вид ( q , p = 1, N )
X l (V nm ) =
- 1+У1 - 4 T qkq + 1 ( V nm ,0 )
GU ( X n , H m , Z , Z , s ) =
4 n ( V nm , s )
l1l 2 P ( V nm , s )
sin H m Z sin X n Z ;
i л л а 4 V nm a q П q (v nm , s ) ■ Л
G 1, q +1 ( X n , H m , Z , Z , s ) = -- ^P ---7---- Sin H m Z Sin X n Z ;
l 1 1 2 P ( V nm , s )
Gq + 11 ( X n , H m , Z , Z , s ) =
4 VnmЛqn(vnm , s) • „ . - „
= M--7П-----Sin Hm Z Sin Xn Z, l112 Qq (V nm , s )
G Ls , p + 1 ( X n , H m , Z , Z , s ) =
A q +1, p + 1 ( V nm , s l ( V nm ) ) =
2T q
V 6 m Л q a p П p ( V
;
’ nm , s l ( V nm ) )
S ’ ( V nm , s l ( V nm ) )
.
Здесь s j ( v nm ) , j = 1,2 N + 2 - нули полинома P ( v nm , s ) ; X l ( V nm ) = s 2 N + 2 + 1 ( V nm ) - дополнительные нули многочлена Q q ( V nm , s ) .
Подставляя теперь (17) и (18) в представления (14), получаем поверхностные функции Грина задачи (6)-(9).
3. Пример
Возьмем для расчета трехкомпонентный ( N = 2 ) материал – дюралюминий, со следующими характеристиками [37]:
Xе = 6,93 ■Ю10 ^Н, ц2 = 2,56 ■Ю10 ^Н;
м 2 м 2
T = 800 К, р = 2780 кг, К 2 = l 22 = 0,01 м;
м 3
D *(1 ) = 7,74 ■ 10 - 14 — , D *(2 ) = 6,67 ■ 10 - 14 —;
n <*) = 0,935, n <2) = 0,045, h 2 = 0,0005 мс;
а2( 1 ) = 1,55 ■Ю 7 Дж, а2( 2 ) = 6,14 ■Ю 7 Дж;
m"1 = 0,027, m ® = ..■■■>'
моль моль
Нагрузку задаем в виде ( H ( т ) - функция Хевисайда)
о 2 N +4 , s
Hq ( X 1 , X 2 , T ) = T Si n "T2" EE 4+ 1,1 ( V n 1 , s l ( V n 1 )) X l 1 l 2 n = 1 l = 1
X
[ exp ( s l (v n 1 )т ) - 1 ][ 1 -(- 1 ) n ] .
----------------------------------Sin X„ x .
X n S l ( v n 1 ) n 1
F ( x , x 2, т ) = - 12 ( q + div m ) = H ( т ) sin n x 2, Fq + 1 ( x 1 , x 2 , T ) = 0.
Результаты вычислений представлены на рис. 2–5. Для расчета использовалось 100 членов ряда Фурье. На рис. 3 изображены пространственно-временные распределения приращений концентраций алюминия, инициированные изгибом пластины. Рис. 3, а позволяет также примерно оценить время, когда массоперенос первой компоненты приобретает статический характер ( т ~3 ■Ю15).
Ниже приводится сравнение полученного решения с решением чисто упругой задачи. В этом случае, полагая в равенствах (16)-(18), (20) Dq = 0 и а = 0, получаем следующие выражения для поперечных смещений:
w =
4 sin Ц) x2
l 1
со E n = 1
sin X nx 1 1 - ( - 1 ) n 1 - cos ( s 01 т )
^ 1 ' ( v n 1 , s 01 ) X n s 01
Подставляя (19) в формулы (10), получаем с учетом равенств (17) и (18)
- 1/2
s 01 = v nm ( v nm + 12 ) .
о 2 N + 2
w ( x1, x2, т) = - sin—2 E E A*) (v n 1, si (v n 1 ))x l1 12 n=1 l=1
[ exp ( s l (v n 1 )т ) - 1 ][ 1 -(- 1 ) ” ] x---------------;---~---------
X n s l ( V n 1 )
sin X nx1,
На рис. 4 продемонстрировано влияние диффузионного поля на поле перемещений.
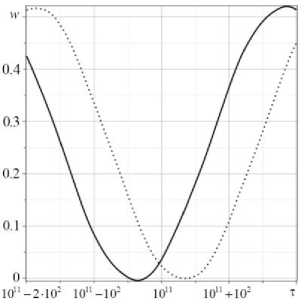
Показано, что начиная с определенного времени упругодиффузионные колебания начинают сдвигаться по фазе относительно упругих колебаний. Примерное начало сдвига ( т ~ 1010) показано на рис. 4, а .
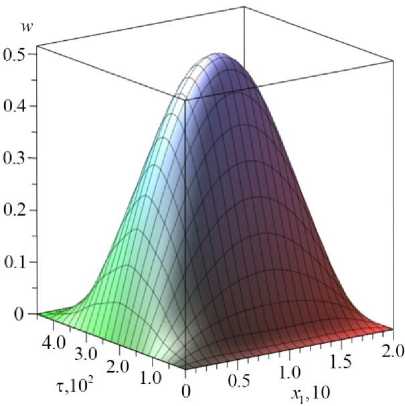
а
Рис. 2. Поперечные смещения пластины: а - w ( x , 0.5 l 2, т ) ;
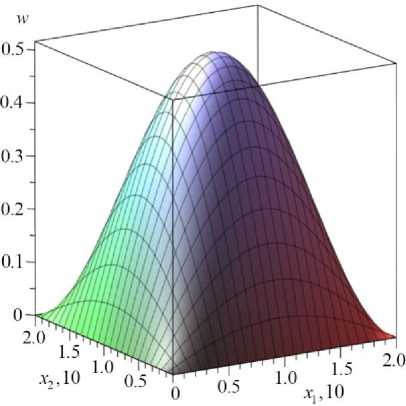
б б - w(x , x2, 2.25 ■Ю2)
Fig. 2. The plate deflections: a - w ( x , 0.5 1 2, т ) ; b - w ( X j , x2 , 2.25 ■ 102 )
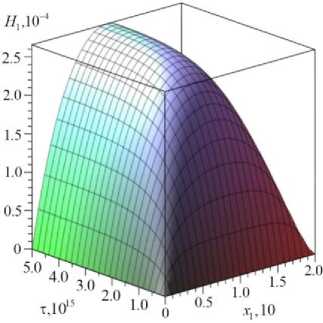
а
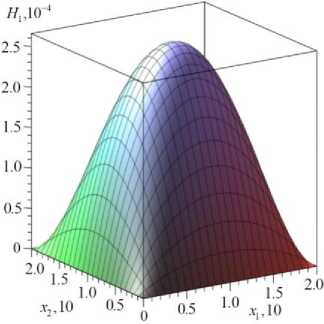
б
Рис. 3. Приращение концентрации первой компоненты (алюминий): а - H ( X ], 0.5 / 2, т ) ; б - H , ( х , х 2, 5 • 10 15 )
5 • IO 15 )
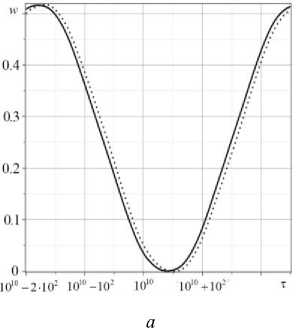
Рис. 4. Поперечные смещения w ( 0,5 / , 0,5 / 2, т ) с учетом массопереноса (сплошная линия) и без него (пунктирная линия): а - те [ 10 10 - 2 • 10 2 ,10 10 + 2,5 • 10 2 ] ; б - те [ 10 11 - 2 • 10 2 ,10 11 + 2,5 • 10 2 ] Fig. 4. The plate deflections w ( 0.5 / , 0.5 / 2, т ) with mass transfer (solid line) and without mass transfer (dashed line): a - те [ 10 10 - 2 • 10 2 ,10 10 + 2.5 • 10 2 ] ; b - те [ 10 11 - 2 • 10 2 ,10 11 + 2.5 • 10 2 ]
Fig. 3. The concentration increment of the first component (aluminum): a - H, ( X j, 0.5 / 2, т ) ; b - Hv ( X j , x 2,
б
а
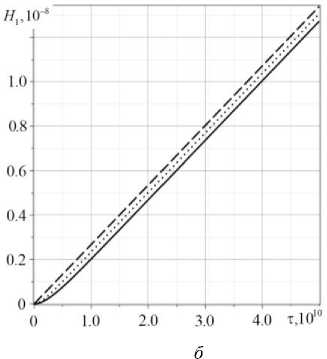
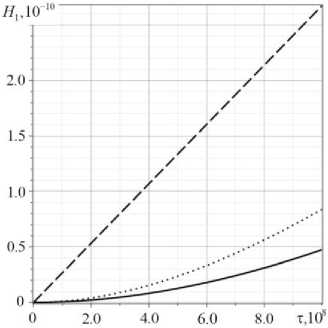
Рис. 5. Приращение концентрации Hv ( 0,1 / , 0,5 / 2, т ) первой компоненты (алюминий): а - те [ 0,10 9 ] ; б - те [ 0, 5 • 10 10 ]
Fig. 5. The concentration increment Hv ( 0.1 / , 0.5 / 2, т ) of the first component (aluminum): a - те[ 0,10 9 ] ; b - те[ 0, 5 • 10 10 ]
Влияние релаксационных эффектов на кинетику массопереноса продемонстрировано на рис. 5. Хорошо видно, что начиная с некоторого момента времени, который соизмерим с временем релаксации τ , релаксационные эффекты начинают затухать (рис. 5, б ).
Заключение
В работе построена математическая модель упругодиффузионных нестационарных колебаний прямоугольной изотропной пластины Кирхгофа–Лява с учетом релаксации диффузионных потоков, описывающая взаимосвязь между механическими и диффузионными полями в сплошных средах. Предложен алгоритм построения поверхностных функций Грина, основанный
Список литературы Упругодиффузионные колебания изотропной пластины Кирхгофа-Лява под действием нестационарной распределенной поперечной нагрузки
- Горский В.С. Исследование упругого последействия в сплаве Сu-Au с упорядоченной решеткой // Журнал экспериментальной и теоретической физики. - 1936. - Т. 6, № 3. - С. 272-276.
- Nachtrieb N.H., Handler G.S A relaxed vacancy model for diffusion incrystalline metals // Acta Metallurgica. - 1954. - Vol. 2, no. 6. - P. 797-802.
- Petit J., Nachtrieb N. H. Self-diffusion in liquid gallium // Journal of Chemical Physics. - 1956. - Vol. 24. - P. 1027.
- Еремеев В.С. Диффузия и напряжения. - М.: Энергоатомиздат, 1984. - 182 с.
- Князева А.Г. Введение в термодинамику необратимых процессов. - Томск: Изд-во «Иван Федоров», 2014. - 172 с.
- Afram A.Y., Khader S.E. 2D problem for a half-space under the theory of fractional thermoelastic diffusion // American Journal of Scientific and Industrial Research. - 2014. - Vol. 6, no. 3. - P. 47-57.
- Aouadi M., Boulehmi K. Partial exact controllability for inhomogeneous multidimensional thermoelastic diffusion problem // Evolution Equations and Control Theory. - 2016. - Vol. 5, no. 2. - P. 201-224.
- Atwa S.Y., Egypt Z. Generalized thermoelastic diffusion with effect of fractional parameter on plane waves temperature-dependent elastic medium // Journal of Materials and Chemical Engineering. - 2013. - Vol. 1, iss. 2. - P. 55-74.
- Boulehmi K., Aouadi M. Decay of solutions in nonhomogeneous thermoelastic diffusion bars // Applicable Analysis. - 2014. - Vol. 93, no. 2. - P. 281-304.
- Choudhary S., Deswal S. Mechanical loads on a generalized thermoelastic medium with diffusion // Meccanica. - 2010. - Vol. 45. - P. 401-413.
- Deswal S., Kalkal K.K., Sheoran S.S. Axi-symmetric generalized thermoelastic diffusion problem with two-temperature and initial stress under fractional order heat conduction // Physica B: Condensed Matter. - 2016. - Vol. 496. - P. 57-68.
- Elhagary M.A. Generalized thermoelastic diffusion problem for an infinitely long hollow cylinder for short times // Acta Mech. - 2011. - Vol. 218. - P. 205-215.
- El-Sayed A.M. A two-dimensional generalized thermoelastic diffusion problem for a half-space // Mathematics and Mechanics of Solids. - 2016. - Vol. 21, no. 9. - P. 1045-106.
- Hwang C.C., Huang I.B. Diffusion in hollow cylinders with mathematical treatment // International Journal of Engineering Research and Development. - 2012. - Vol. 3, iss. 8. - P. 57-75.
- Knyazeva A.G. Model of medium with diffusion and internal surfaces and some applied problems // Mater. Phys. Mech. - 2004. - Vol. 7, no. 1. - P. 29-36.
- Kumar R., Chawla V. A study of Green’s functions for three-dimensional problem in thermoelastic diffusion media // African Journal of Mathematics and Computer Science Research. - 2014. - Vol. 7, no. 7. - P. 68-78.
- Kumar R., Devi S., Sharma V. Plane waves and fundamental solution in a modified couple stress generalized thermoelastic with mass diffusion // Materials Physics and Mechanics. - 2015. - Vol. 24. - P. 72-85.
- Othman M.I.A., Elmaklizi Y.D. 2-D problem of generalized magneto-thermoelastic diffusion, with temperature-dependent elastic moduli // Journal of Physics. - 2013. - Vol. 2, no. 3. - P. 4-11.
- Sharma J.N., Sharma N.K., Sharma K.K. Transient waves due to mechanical loads in elasto-thermo-diffusive solids // Advances in Applied Mathematics and Mechanics. - 2011. - Vol. 3, no. 1. - P. 87-108.
- Sherief H.H., El-Maghraby N.M. A Thick plate problem in the theory of generalized thermoelastic dffusion // Int. J. Thermophys. - 2009. - Vol. 30. - P. 2044-2057.
- Швец Р.Н., Флячок В.М. Уравнения механодиффузии анизотропных оболочек с учетом поперечных деформаций // Математические методы и физико-механические поля. - 1984. - Вып. 20. - С. 54-61.
- Швец Р.Н., Флячок В.М. Вариационный подход к решению динамических задач механотермодиффузии анизотропных оболочек // Математическая физика и нелинейная механика. - 1991. - № 16. - С. 39-43.
- Aouadi M. Copetti M.I.M. Analytical and numerical results for a dynamic contact problem with two stops in thermoelastic diffusion theory // ZAMM Z. Angew. Math. Mech. - 2015. - P. 1-24. doi: 10.1002/zamm.201400285.
- Copetti M.I.M., Aouadi M. A quasi-static contact problem in thermoviscoelastic diffusion theory // Applied Numerical Mathematics. - 2016. - Vol. 109. - P. 157-183.
- Aouadi M. Miranville A. Smooth attractor for a nonlinear thermoelastic diffusion thin plate based on Gurtin-Pipkin’s model // Asymptotic Analysis. - 2015. - Vol. 95. - P. 129-160.
- Aouadi M. On thermoelastic diffusion thin plate theory // Appl. Math. Mech. -Engl. Ed. - 2015. - Vol. 36, no. 5. - P. 619-632.
- Aouadi M., Miranville A. Quasi-stability and global attractor in nonlinear thermoelastic diffusion plate with memory // Evolution Equations and Control Theory. - 2015. - Vol. 4, no. 3. - P. 241-263.
- Bhattacharya D., Kanoria M. The influence of two temperature generalized thermoelastic diffusion inside a spherical shell // International Journal of Engineering and Technical Research (IJETR). - 2014. - Vol. 2, iss. 5. - P. 151-159.
- Zemskov A.V., Tarlakovskii D.V. Modelling of rectangular Kirchhoff plate oscillations under unsteady elastodiffusive perturbations // Acta Mechanica. - 2021. doi: 10.1007/s00707-020-02879-1
- Afanasieva O.A., Zemskov A.V. Unsteady elastic-diffusion oscillations of a simply supported kirchhoff plate under the distributed transverse load action // Gdoutos E., Konsta-Gdoutos M. (eds) Proceedings of the Third International Conference on Theoretical, Applied and Experimental Mechanics. ICTAEM 2020. Structural Integrity. - Vol. 16. - Springer, Cham, 2020. - P. 181-186.
- Le K.C. Vibrations of shells and rods. - Berlin, Springer Verlag, 1999. - 425 p.
- Михайлова Е.Ю., Тарлаковский Д.В., Федотенков Г.В. Общая теория упругих оболочек. - М.: МАИ, 2018. - 112 с.
- Igumnov L.А., Tarlakovskii D.V., Zemskov A.V. A two-dimensional nonstationary problem of elastic diffusion for an orthotropic one-component layer // Lobachevskii Journal of Mathematics. - 2017. - Vol. 38, no. 5. - P. 808-817.
- Земсков А.В., Тарлаковский Д.В. Двумерная нестационарная задача упругой диффузии для изотропного однокомпонентного слоя // Прикладная механика и техническая физика. - 2015. - Т. 56, № 6. - С. 102-110 = Zemskov A.V., Tarlakovskiy D.V. Two-dimensional nonstationary problem elastic for diffusion an isotropic one-component layer // Journal of Applied Mechanics and Technical Physics. - 2015. - Vol. 56, no. 6. - P. 1023-1030.
- Tarlakovskii D.V., Vestyak V.A., Zemskov A.V. Dynamic processes in thermoelectromagnetoelastic and thermoelastodiffusive media // Encyclopedia of Thermal Stress. - Vol. 2. - Springer Dordrecht Heidelberg; New York, London, Springer reference, 2014. - P. 1064-1071.
- Диткин В.А., Прудников А.П. Справочник по операционному исчислению. - М.: Высшая школа, 1965. - 586 с.
- Физические величины: справочник / А.П. Бабичев, Н.А. Бабушкина, А.М. Братковский [и др.] / под общ. ред. И.С. Григорьева, И.З. Мелихова. - М.: Энергоатомиздат, 1991. - 1232 с.


