Упругое равновесие тяжелого горизонтального толстостенного ортотропного цилиндра, находящегося под действием неравномерно распределенного бокового давления

Рассмотрим равновесие тяжелого горизонтального толстостенного ортотропного цилиндрического тела, которое находится под дей ствием неравномерно распределенного давления, заданного на внеш-

Рис. 1. Тяжелый ортотропный цилиндр, находящийся под действием неравномерного бокового давления

ней боковой поверхности. На рис. 1 представлена расчетная схема задачи. В силу бесконечной протяженности тела радиальные и окружные перемещения ( и и v ), радиальные ( ст rr и £ rr ), окружные ^{( ст} ее ^{и £} ее )» ^{осевые ( ст} _zz ) ^нормальных напряжения и деформации, касательные напряжения и сдвиговые деформации ( ст rz и £ rz ) не зависят от осевой координаты z .

Действующее на внеш нюю поверхность тяжелого цилиндра неравномерное давление задается функцией R (е), симметричной относительно вертикальной централь- ной плоскости. Однако в рассматриваемом ниже частном случае на закон распределения R (6) накладываются следующие ограничения:

2 л	R ( 6 ) , л<6< 3 л ;
J o*- cos 6 d 6 — -л ( b 2 - a 2 ) р , с Гг —‘ 0	22 0,   3 ^<0<— , I           2        2

вызванные тем, что эта нагрузка является реакцией основания на действие собственного веса. Здесь р - удельный вес материала, а и b -внутренний и внешний радиусы тяжелого цилиндра.

Запишем неоднородную систему уравнений Ламе для тяжелого ортотропного цилиндрического тела:

2    22        2    2   2     2   22

= -^P- cos 6 ,(2)

K ₁₁

о u m о и 1 о u n n + m о v q + m о v

—~ +—---~ +-----— и--1---1--- оr2 r2 562 r оr r2       r2   56 r    оr56

о ² v  p ² о ² v   1 о v   v   k ² + 1 о ² и   p ² + 1 о и      р . „

+      +    —т+         +        =-   sin 6, ог2   г2 о62  r оr  r2     r  оrо6    r2  о6    Gr6

которая была получена последовательной подстановкой определяющих

°rr — K11£rr + K12B66 , °66 — K12£rr + K22^66 , Tr6 — Gr6^r6

и геометрических соотношений Коши о и и  1 о v        1 о и  о vv

в rr

, В —1 , у —1

оr   66 r  r о6   r6   r о6  оrr в уравнения равновесия do„. 1 отг6 о - о00        „ 1 оа00 отг6 _ т

—— +--— + — rr ---⁶⁶ — р cos 6,--⁶⁶ + —— + 2 - r ⁶ — -р sin 6 , (5)

оr   r о6 r              r о6 оr r содержащие компоненты вектора массовых сил Fr — -р cos 6

и F 6 — р sin 6 . Выражения (2) и (3) содержат следующие коэффициенты:

m —

G r O _{n —}

^K 11 ^,

^K 22

^K 11

q ^—

^K12 п _— K 22 k _— K 21

V K _п ^, p V G r 6 ^, GGr 6 ^,

EEE

^K 11 ^— d ^{( 1}   ^ 6 z Н z 6 ⁾ , K 22 ^— d ^{( 1} Ц rz H zr ^{) , K} 12 ^— d ⁽ ^ r 6 ⁺ Ц rz Ц z 6 ^{) ,}

D — 1 - 2цr6H6zHzr - Hr6^6r - H6zHz6 - HzrHrz , где Er, E6 и Ez - модули Юнга в направлениях r, 0 и z ; цr6, ц6z и цzr - коэффициенты Пуассона; Gr0 - продольный модуль сдвига. Осевые напряжения сzz не являются независимыми, а определяются при помощи равенства

^Ц rz      I ^Ц z 0 ГТ

³ zz ^- E z      ³ rr ^{1     3}UU •

I E r       E 0     )

Симметрия нагрузки относительно вертикальной плоскости, проходящей через образующую, и геометрическая симметрия тяжелого цилиндрического тела предопределяют поиск решения системы дифференциальных уравнений (2) в виде тригонометрических рядов по окружной координате:

да                               да u= E ui (r ) cos i 0, v= E vi ( r ) sin i 0,(6)

i-0

подстановка которых в исходную систему позволяет записать:

Е | u, + — Г u, +i^2 + m2\v Л—уГ( m2i2 + n2^Uj + i(n2 + m2^v, 1 cos i б!-i rV i                        i J L                     ii i-0        r                                r)

--^- cos 0 , ^K 11

да

E i-0 I

v "+—Г v i ' - i ( k ² + 1) u i 'J—уL ( P ² i 2 + 1) v i + i ( P 2 + 1) u i Jj sin i 0-- G -sin0.

Обратим внимание на то, что система обыкновенных дифференциальных уравнений (7) однородна при i - 0 и i >  1, неоднородна при i - 1 • Поэтому для различных i решение системы (7) можно рассматривать независимо и представить поля перемещений и напряжений в тяжелом цилиндре в виде суперпозиции:

да                                       да u - u0 + u1cos 0 + ^ uicos i0 , v - v1cos 0 + ^ visin i0 , i-2                                i-2

да , ,                                     , .                    да , .

с _rr -с Г 0 ⁾ +o rr ^cos 0 + ^ a rr ^cos i 0 , т _{r 0} - т Г ₀ ⁾ cos 0 + ^ x r ^sin i 0 , (8)

i - 2

i - 2

Разложение (8) позволяет выделить механический смысл каждого из слагаемых. Так, например, слагаемые с индексом i = 0 отражают вклад равномерно распределенной нагрузки на внутренней и/или внешней боковой поверхности цилиндрического тела и соответствуют решению «классической» задачи Ламе. Слагаемые при i = 1 позволяют учесть гравитационные силы, а при i >  1 - неравномерно распределенной нагрузки, которую перед подстановкой в граничные условия необходимо разложить в тригонометрические ряды по окружной координате.

При i = 0 отсутствуют окружные перемещения ( г ₀ = 0 и, как следствие - v 0 = v 0 = 0 ) и касательные напряжения ( т . 0д = 0 ), а единственное уравнение системы (7)

u о

⁺ - ( u 0

r

- n ² и 0 j = 0

имеет общее решение и 0 = C rn +   ,                         (10)

rn где n = д/К22/К-I - «классический» показатель анизотропии [3].

Решение системы дифференциальных уравнений (7) при i = 1 представим в виде

U 1 = U ) + и_х , v 1 = v + v * ,                        (11)

суперпозиции общего решения соответствующей однородной системы «1, v и одного из частных решений неоднородной системы

*   0   2 * to 0 — 1           Мт G_r о + ®2 К

U 1      Р . ², v = —     Р . ², ⁰ =          2^4 ,    (¹²)

G r е              ^to 3 G r е              ^К11 ( ^to 1 ^to 3 ^{+ to} 2 ^to 4 )

где to1 = 4 — m2 — n2, to2 = 2q2 + m2 — n2 , to3 = 3 — p2, to4 = 2k2 + p2 + 3.

Решение однородной системы при i >  1 будем искать в виде обобщенных степенных рядов:

да                         да u = Е J+v, v = Е bjrJ+v ■              (13)

j = 0                J = 0

Это позволяет записать выражения для радиальных и окружных перемещений следующим образом:

U1 = | “1r В + a2 + аз1п r + a4 + Br2 I cos 0,(14)

V       rВ)

I _ В 0

v = I a^r + a 2 —j^ + a 3 О 3Ш r + a 4 0 4 + Ar I sin 0 ,

V            rВ)

u

( i > 1 )

”

= SI “1r% i=2 V

a?          ф,-     a I

+ —+ + a_Ar ^ф i +— 4- cos i 0 , _r^s i     ³ _гф i J

v ⁽ i > ^{1 )}

да /

= S I a l ^ li r ^S i i = 2 ^V

Wn        ф, W 1

+ a 2 к + a 3 W 3 F + a 4 — ^4L I sin i 0 , r ^s i                        r ^ф i )

где

в( k2 +1) + p2 +1       p2 +1 -в( k2 +1)

«1 =    —A Г“ ’ a2 = 9 / о F, a3 = a4 = -1,В2-(p2 +1)             В2-(p2 +1)

^В = Л K 22

I 1

1 I

^S i V

+

V A 11    G r 0 )

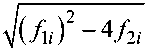
^^^^H

K

K 12 2 + K 12

K 11 V

ф V

\

G r 0 )

^{+ 1},

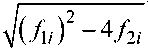
i [(k2 + 1)s i + p2 +1]         i [ p2 +1 -(k2 + 1)s i ]

=     s 2 - p ² i ² - 1     ^{, W 2 i} =     s 2 - p ² i ² - 1

_ i [ ( ^{k 2 + 1} ) ф i ⁺ p ^{2 + 1} ]       _ i [ p ^{2 + 1 -} ( ^{k 2 + 1} ) ф i ]

=     ф 2 - p ² i ² - 1     ^{, W} 4 =     ф 2 - p ² i ² - 1

^f 1 i = i

K 22 - K ^{12 1} K ¹² - 2 )1 + 1, f   i 4 ⁴ - 2 i ² + 1 K ²²,

G r ₈    K 11 V G r 0     )] i ⁽           ' K 11

метральной плоскости. Эта зависимость является следствием появления сдвиговых деформаций, которые отсутствуют в случае, когда и нагрузка, и само тело обладают одной и той же осью симметрии.

Обратим внимание на то, что в выражениях (16) для параметров £ i и ф i под знак квадратного корня входят комплексы, состоящие из упругих модулей материала. Поскольку вышеперечисленные параметры должны принимать только действительные значения, можно записать ограничения в форме неравенств на возможные величины упругих модулей материала и условия существования решения при i >  1:

K ²² ₊ i 2

K 11

K ₂₂

G r 6

i ²

K ₁₂

K 11

K ₁₂

V G r 6

- 2

K ₂₂ K ₁₂ ^^^^^^^^^^^^^^^^^e ^^^^^ ^^^^^^^^^^^^^^^^e

G r 6

K 11

+ 1 >+ 2 ( i ⁴

K ₁₂

V G r 6

- 2

+ 1 >  0 .

2 i ² + 1) K ²², ⁵ K 11

В частном случае E r = E ₆ = E z = E , p _{r 6} = p ₆ z = p _zr = p и G r 6 = G = E /[ 2 ( 1 + v ) ] , который соответствует изотропному тяжелому горизонтальному цилиндру, новое аналитическое решение совпадает с результатом, полученным автором [2] с точностью до коэффициентов любого частного решения. Учет анизотропии материала позволяет установить связь между коэффициентами, входящими в равенства (12):

О _ю₄ О- 1_ р G_{r 6} « з G r ₆ 2 E

^{1 -p- 2} ( ^p ) 2

Покажем одно из возможных приложений найденного аналитического решения на примере задачи о равновесии тяжелого железобетонного цилиндра, наполовину закопанного в грунт. Предположим, что площадь контактной поверхности и реакция основания известны и неизменны во времени, а сама реакция распределена по боковой поверхности цилиндра по параболическому закону

R (6) = A 62 + B 6 + C. (17)

Тогда, воспользовавшись условиями (1), можно определить коэффициенты уравнения (17) и записать частный вид реакции следующим образом:

R (0) = 116 (b2 - a2 )(8—0-3—2 - 4 О2 )р.

Представим решение задачи для бесконечно протяженного тяжелого толстостенного ортотропного цилиндрического тела со свободной от нагрузок внутренней поверхностью, которое находится на грунтовом основании, в виде суперпозиции решений: «классической» задачи Ламе ( i = 0), задач о равновесии тяжелого цилиндра с жестко закрепленной внешней и свободной от напряжений внутренней боковой поверхностью ( i = 1) и, наконец, с жестко закрепленной внутренней поверхностью и заданным неравномерным давлением на внешней поверхности ( i >  1).

Закрепление цилиндров по внутренней или внешней поверхности приводит к появлению на этих участках дополнительных реакций, суммарный вклад которых

2л

Ra = j^^

2л

cos I 0 + — I d0 , Rb = f o^

r = a     I 2

cos 0 d 0 .

r = a

Поскольку исходная задача не предполагает каких-либо условий закрепления, необходимо скомпенсировать реакции (19). Для этого предположим, что неоднородная реакция на закрепленной поверхности может быть заменена эквивалентной равномерно распределенной нагрузкой интенсивностью

Тогда граничные условия для рассматриваемой суперпозиции краевых задач можно представить следующей группой равенств:

( i =0 ) = ^- P a ^- q a , ^Q r ’

r = b

г = b

( ^z'^: = V^v

r = b

0, Q i

r = a

⁽ i =

0, ^T r 0

r = a

и ( i >1 )

u

(i >1) = vA r=a

= 0, o^1^

r = a

r = b

( i >1 )

= a i cos i 9 , т Г ₆ '

= 0, r = b

где a i = ( - 1 ) i ( a²

^^^^^^^^

b ² ) p ji ² - коэффициенты разложения реакции ос-

нования в тригонометрический ряд по окружной координате. Эти условия позволяют определить постоянные интегрирования общих решений (10), (14) и (15).

Обратим внимание на то, что граничные условия (20) позволяют скомпенсировать дополнительные реакции только в радиальном направлении. Несмотря на то что при закреплении внутренней или внешней боковой поверхности возникают усилия в окружном и осевом направлениях, попытка компенсации этих реакций привела бы к получению решения с точностью до константы, отвечающей либо за вращение тяжелого цилиндра как жесткого целого вокруг оси симметрии, либо за перемещение в вертикальном направлении.

На рис. 2 представлено распределение перемещений точек поперечного сечения монолитного железобетонного цилиндра на внутренней, внешней и серединной поверхности по окружной 0 и обезразме-ренной радиальной p = ( r - a )/( b - a ) координатам. Были выбраны следующие параметры геометрии тела и упругие постоянные железобетона: a = 3,0м и b = 5,5 м; E_rr = 4 - 10⁵МПа, E ₆₆ = 8 - 10⁵МПа, E zz = 5,33 - 10⁵ МПа, G_{r 6} = 5,65 - 10⁴ МПа, ц _{е r} = 0,15, ц _rz = 0,075 и ц z 6 = 0,375 .

Распределения перемещений по окружной координате носят немонотонный характер. Окружные перемещения являются нулевыми в точках, принадлежащих вертикальной диаметральной плоскости, в точках на внутренней, серединной и внешней поверхностях верхнего свода положительны, принимают свои максимальные значения при 6 = 90 ° , 6 = 60 ° и 6 = 45 ° . На нижнем своде в точках 6 = 125 ° , 6 = 115 ° и 6 = 125 ° происходит смена знака, а 6 = 125 ° , 6 = 115 ° и 6 = 125 ° соответствуют точкам минимума для этих перемещений v на внутренней, серединной и внешней поверхности.

Радиальные перемещения на верхнем своде минимальны, возрастают по величине при увеличении окружной координаты. Эти перемещения на внутренней поверхности цилиндра всюду положительны, на серединной поверхности принимают положительные значения до 0 = 168° и имеют максимумы при 6 = 180° и 6 = 120° соответственно. На внешней поверхности зависимость и от окружной координаты такова, что отрицательные значения имеют место при 0° <6< 15° и 160° < 6 < 180°, а максимальные значения достигаются при 6 = 115°.

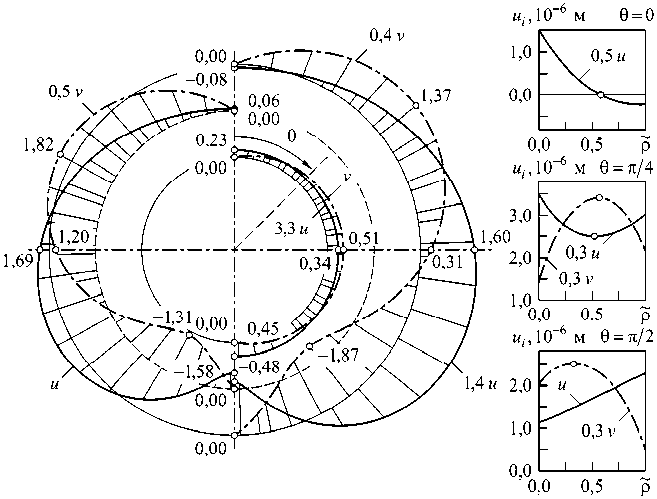
Рис. 2. Распределение радиальных ( и , 10 ⁶ м) и окружных ( v , 10 ⁶ м) перемещений в монолитном железобетонном цилиндре на внутренней, внешней и серединной поверхностях

Характер зависимостей перемещений точек, принадлежащих верхнему своду тяжелого цилиндра в направлении обезразмеренной радиальной координаты существенно изменяется при увеличении угла 6 . Перемещения и монотонно убывают при 6 = 0, монотонно возрастают при 6 = л/2 и имеют точку локального минимума при 6 = л/4. Зависимости v~ р имеют локальные максимумы, положение которых смещается ко внутренней поверхности цилиндра при увеличении окружной координаты.

Обратим внимание на еще одну закономерность распределения радиальных перемещений. Производные и по окружной координате

5 u

ao

^^^^H

a 1 r ^ + a 2 + ^a 3 ln r + ^a 4 + Br^ r ^p

sin 0

^^^^H

TO

"D

i =2

a 1 r ^b i

⁺ a ^ + a з r ⁹ r ь i

a I

+ -4- sin i 0

r ⁹ i )

принимают нулевые значения

5 u

50 r = a

0=0

5 u     5 u

50 r = a   50 r = ( a + bM^

0=л      0=0

5 u

50 r =( a + b )/ ^ 0=л

5 u     5 u

50 r = b 50 r = b

0=0      0=л

в точках поперечных сечений тяжелых ортотропных цилиндров, принадлежащих вертикальной диаметральной плоскости. Этот результат не зависит от того, на каком расстоянии от оси вращения находится рассматриваемая точка.