Упругопластические колебания стержневой системы с учётом продольной податливости её элементов при запроектном воздействии

Введение. Одной из актуальных проблем, связанной с расчётами современных конструкций (особенно при динамических воздействиях), является проблема учёта работы материала за пределом упругости. Экспериментальные исследования в этом направлении показывают, что характер работы различных материалов может быть довольно сложным [1]. Несмотря на это, на сегодняшний день разработаны и внедрены в практику вычислительные методы, позволяющие проводить расчёты в такой постановке [2–4].

Однако большинство используемых методов построено на численных подходах. С одной стороны, это делает возможным решение широкого спектра задач, а с другой – остаётся открытым вопрос адекватности результатов расчётов и оценки действительного состояния конструкций.

В связи с этим по-прежнему актуальной является разработка аналитических подходов для решения подобных задач. Наиболее естественным является метод временного анализа, основанный на исследовании характеристического матричного квадратного уравнения [5].

В данной статье рассматривается проблема расчёта систем указанным методом с учётом упругопластической работы материала при действии динамических нагрузок. Приводится пример расчёта статически нагруженной плоской стальной ферменной конструкции при действии импульсной нагрузки и даётся анализ работы системы.

Математическая модель упругопластического расчёта. Физическая модель материала принята по билинейному закону в координатах ст ~ £ (рис. 1). В осях «восстанавливающая сила -относительное перемещение» ( R ~ у ), вектор динамических восстанавливающих сил выражается зависимостью (рис. 2):

R ( t ) = R ke ( t ) + R u ( j - R p ( t j ). (1)

Эта формула представляет собой математическую модель расчёта системы при упругопластическом деформировании её несущих элементов.

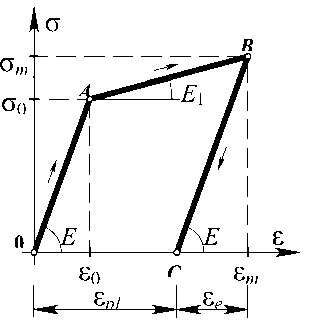
Рис. 1. Диаграмма деформирования материала

Представим характеристику векторных величин правой части выражения (1).

Составляющая R ke ( t ) = K ( t j ) • Y ( t ) - вектор квазиупругих усилий, где K ( t_j ) – матрица жёсткости системы в момент t_j (точка A на диаграмме), – время перехода квазиупругой системы из одного промежуточного состояния в другое (начало текучести в некотором несущем элементе). Здесь tgα, tgα 1 – жёсткость некоторого несущего элемента, соответственно, на участках OA и AB .

Составляющая R u ( t j ) = A K ( t j ) • Y ( t j ) - есть вектор предельных значений (на рис. 2 приведена k -я компонента этого вектора), где A K ( t j ) = K ( t j - 1 ) - K ( t j ) - разность матриц жёсткости, соответствующих предыдущему (участок OA ) и текущему(участок AB ) состояниям системы.

Составляющая R p ( t j ) = K ( t j ) • Y p ( t j ) - суть вектор остаточных усилий. При достижении экстремальных деформаций (в момент времени t _j ) в несущем элементе начинается разгрузка (участок BC ). В результате этого он приобретает необратимые остаточные напряжения и деформации, что в координатах R ~ y выражается векторами R p ( t j ) и Y p ( t j ), постоянными на интервале [ t j , t j + 1 ] , где Y_p ( t_j ) – вектор пластических перемещений.

Численная реализация задачи. В качестве примера рассмотрена задача колебаний плоской ферменной конструкции как системы с двумя степенями свободы (n=2), расчётная динамическая модель (РДМ) которой представлена на рис. 3. Элементы системы имеют квадратные поперечные сечения со сторонами: 1 – 2,6 см, 2 – 1,0 см, 3 – 2,5 см и выполнены из стали 09Г2С с начальным модулем упругости E = 210060 МПа. Точечная масса принята m = 10 т. Векторы перемещений и узловой статической нагрузки, а также матрица масс имеют вид:

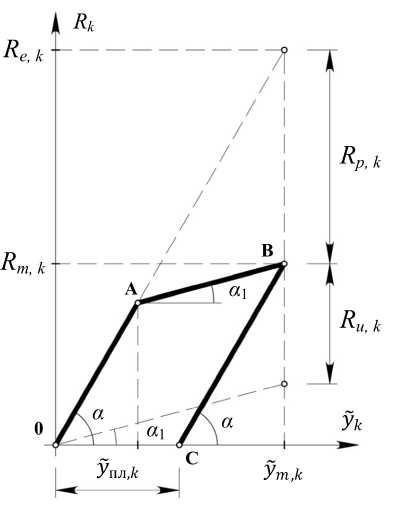
Рис. 2. Составляющие вектора динамических восстанавливающих сил R

Y ( t ) =

y ₁( t ) y ₂( t )

Q = mg

m

M =

m

Элементы матрицы жёсткости K ( t_j ) вследствие нелинейности задачи, обусловленной моделью (1), вычисляются в процессе временного анализа с использованием пособия [6]. Матрица демпфирования C строится по модели непропорционального демпфирования [5] и вычисляется в процессе временного анализа совместно с матрицей жёсткости.

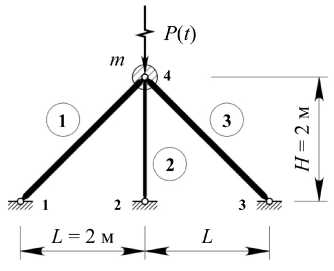
Рис. 3. Расчетная схема конструкции

Таким образом, описанная математическая модель позволяет разбить процесс временного анализа на ряд квазиупругих интервалов [ t j , t j + 1 J ( j = 0,1,... ) , внутри которых составляющие вектора восстанавливающих сил R_u ( t_j ) и R_p ( t_j ) представляют собой постоянные величины. В результате такого моделирования уравнение движения дискретной диссипативной системы на отдельном интервале можно реализовать по схеме упругого решения:

MY ( t ) + CY ( t ) + K ( t j )Y ( t ) =

= P ( t ) + Q - R „ ( t j ) + R_p ( t j ). (2)

Так как векторные добавки R_u ( t_j ) и R_p ( t_j ) представляют собой силовые характеристики, действующие на массы системы, то их внезапное появление или исчезновение, связанное с упругопластическими процессами в материале, будет приводить к изменению ускорений масс, дополнительные значения которых равны M -¹ •[ R p ( t j ) - R ( t j .) ] .

Внешняя нагрузка представлена в виде синусоидального импульса P ( t ) = P ₀ - sin( 0 1 ), где P 0 = [0, 425] Т кН - вектор амплитуд, 0 = п / t a ; t a = 0,01 с -время действия импульса.

Система разрешающих уравнений динамической задачи (2) на квазиупругом интервале t е [ t j , t j _{+ 1} ] имеет вид:

y ( t ) = 2Re { Z ( t )}, Y ( t ) = 2Re { S·Z ( t )},       (3)

где

' Z ( t ) = 0,5 Y t + 2 0 ( t - t j ) + Z^QR ( t - t j ) + Z P ( t - t j ), Z^QR ( t - t j ) = [ Ф ( t - t j ) - E ] ( US ) "1 [ Q - + ],

- 2 ₀( t - t j ) = Ф ( t - t j ) U -1 М [-Y 0 + ],                (4)

Z P ( t - t j ) = { S [ Ф ( t - t j ) sin( qt j ) - sin ( qt )] + + [ Ф ( t - t j ) cos( qt j ) - cos( qt )] q }[ U ( S ² + Eq 2 )]"¹ P ₀.

Здесь Yst = K–1Q,Ф(t) = eSt, U= MS + SТM+ C,S – матрица внутренних характеристик конструкции – решение матричного характеристического уравнения, соответствующего системе однородных диф- ференциальных уравнений с постоянными коэффициентами (2) [5]; y0, Y0 – векторы начальных условий.

Временной анализ реакции проводится на интервале времени t = [0, 5] с при шаге интегрирования A / =0,0001 с . При заданных условиях работы нелинейные колебания происходят в наиболее нагруженном 2-м элементе фермы (рис. 3), в то время как остальные стержни работают упруго. Упругопластические процессы во 2-м стержне протекают в течение первых 0,15 секунд и, главным образом, на этапе свободных колебаний, после чего система переходит в режим упругих колебанийс учётом накопленных пластических деформаций.

Нелинейная стадия работы характеризуется тем, что система находится в состоянии циклического упругопластического деформирования. За наступившими пластическими деформациями следует разгрузка, затем этот процесс неоднократно повторяется, что свидетельствует о гистерезисном поведении зависимости а ~ 8 . На рис. 4 показана первая петля гистерезиса с характерными точками, отделяющими линейные участки друг от друга. Эти же точки, согласно представленной математической модели расчёта (1), находятся в соответствии с временными точками, расчленяющими процесс упругопластической реакции системы на ква-зиупругие интервалы (см. таблицу).

В упругой стадии (при t > 0,15 с )свободные колебания системы совершаются относительно нового положения равновесия, которое отличается от первоначального положения статического равновесия Y_st ( t ) тем, что к последнему добавляются остаточные перемещения – компоненты вектора Y_p ( t ) , накопленные системой в процессе пластического деформирования.

При реализации разрешающих уравнений (3), (4) положения характерных точек диаграммы (рис. 4) (с учётом одинаковой работы материала на растяжение-сжатие) находятся следующим образом. Точка A определяется из условия достижения нормальными напряжениями в среднем стержне предела текучести σ₀, а положение точки B – из условия достижения в нем экстремальных деформаций. Нахождение точки D связано с использованием принципа Мазинга [1], согласно которому переход к неупругому деформированию во втором полуцикле происходит после упругого деформирования на величину, равную двум пределам текучести. То есть суммарное напряжение (расстояние между точками B и D ) не должно превышать 2σ₀. Положение точки E , как и точки B , определяется из условия достижения экстремума деформаций.

Анализ результатов. На рис. 5 показаны осциллограммы перемещений (а), ускорений (б) и восстанавливающих сил (в). Цифры обозначают направление колебаний: 1 – по горизонтали; 2 – по вертикали.

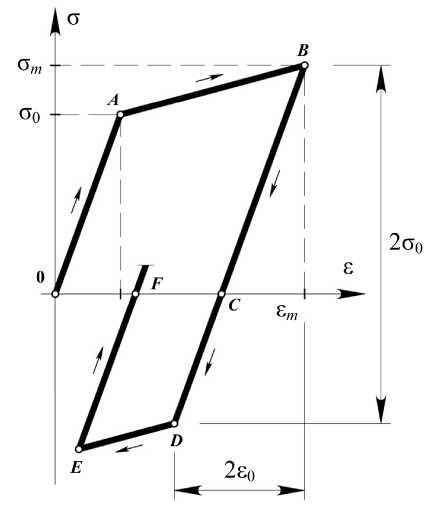
Рис. 4. Диаграмма деформирования 2-го стержня фермы за один полный цикл на интервале времени t = [0; 0,0874]

Временные точки переходов системы в новые состояния

Точки диаграммы (рис. 4)	Время t , с
0	0
A	0,0098
B	0,0265
C	0.0455
D	0,0584
E	0,0680
F	0,0874

Осциллограмма вертикальных перемещений массы m (рис. 5, а) представляет собой график без переломов и разрывов. При этом колебания совершаются относительно ненулевой асимптоты, высота которой меняется при переходе от одного квазиупругого интервала к другому. После t = 0,15 с высота асимптоты остаётся постоянной и равна y_st ,2 + y p ,2 =- 0,2038 см, где y_st2 =— 0,167 см - статический прогиб в начальный момент времени, y p , ₂ =- 0,0368 см - вертикальная компонента вектора остаточных перемещений. Для колебаний массы в горизонтальном направлении характерны те же эффекты, что и для вертикальных колебаний, но они выражены значительно слабее.

В отличие от графиков перемещений осциллограммы ускорений (рис. 5, б) не имеют смещения относительно положения статического равновесия системы. На фрагментах графика ускорений масс в

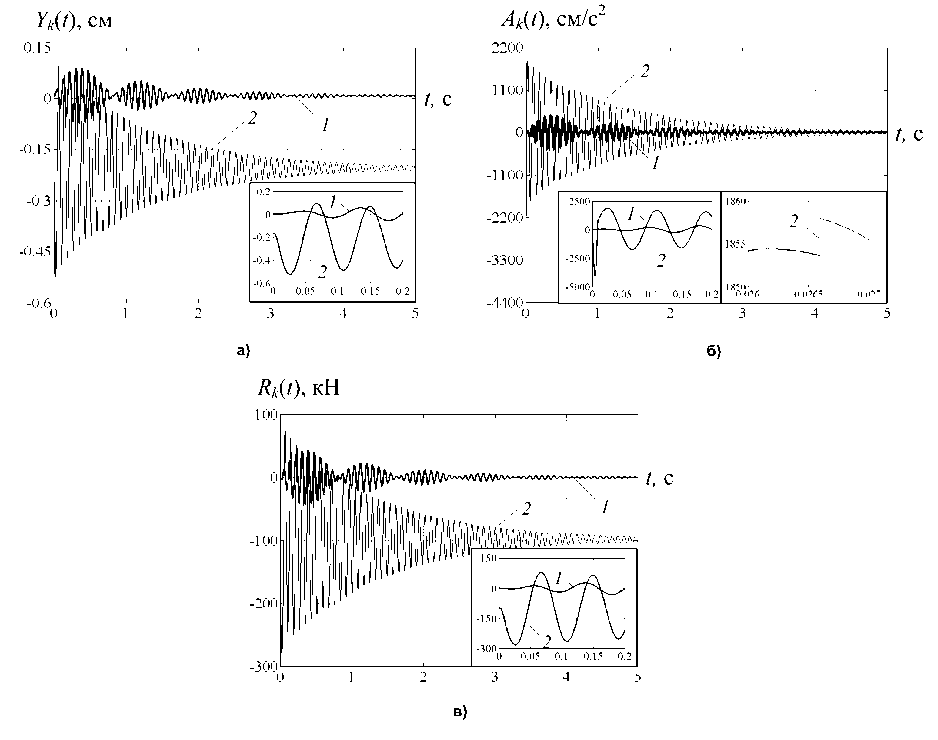
Рис. 5. Параметры реакции системы (1 – по горизонтали, 2 – по вертикали): а – перемещения; б – ускорения; в – восстанавливающие силы

вертикальном направлении можно видеть перелом, связанный с окончанием действия импульсной нагрузки при t = 0,01 с (фрагм. 1), и один из скачков (фрагм. 2). Скачки образуются в результате внезапного изменения жёсткости системы.

Осциллограммы восстанавливающих сил R ( t ) (рис. 5, в ), как и осциллограммы перемещений, являются непрерывными. Компоненты восстанавливающих сил в горизонтальном направлении имеют нулевую асимптоту, в вертикальном направлении – асимптоту, соответствующую значению статического усилия от собственного веса конструкции Q .

Характер свободных колебаний всех параметров реакции – затухающий. При этом осциллограммы, соответствующие горизонтальным параметрам, имеют форму «биения», период которого составляет:

Ю 2 - Ю 1

2 п

76,69 - 69,3

= 0,82 с,

где ю1, ю2 - частоты собственных колебаний кон- струкции.

На рис. 6 показан график действующих вертикальных сил правой части уравнения (2). Пунк- тирной линией (а) изображена составляющая нагрузки правой части, включающая внешнюю нагрузку: импульсную P(t) и статическую (собственный вес Q). Сплошной линией (б) изображена полная нагрузка, включающая, помимо внешней, добавки к восстанавливающим силам Ru(tj) и Rp(tj):

L P i ( t ) = P ( t ) + Q - R ( j + R p ( t j ).

Данная нагрузка имеет ступенчатый характер, который связан с внезапным появлением или исчезновением составляющих R_u ( t_j ) и R_p ( t_j ) , что обусловлено принятой математической моделью упругопластического расчёта (1).

Выводы

• 1.    Временной анализ позволяет получить точное решение задачи в аналитическом виде.

• 2.    В замкнутой форме построены кинематические и силовые параметры реакции системы для динамической задачи с билинейной диаграммой деформирования гистерезисного типа.

• 3.    Определены и изучены особенности поведения параметров реакции динамической системы: асимптоты, переломы, скачки и т. д.

  

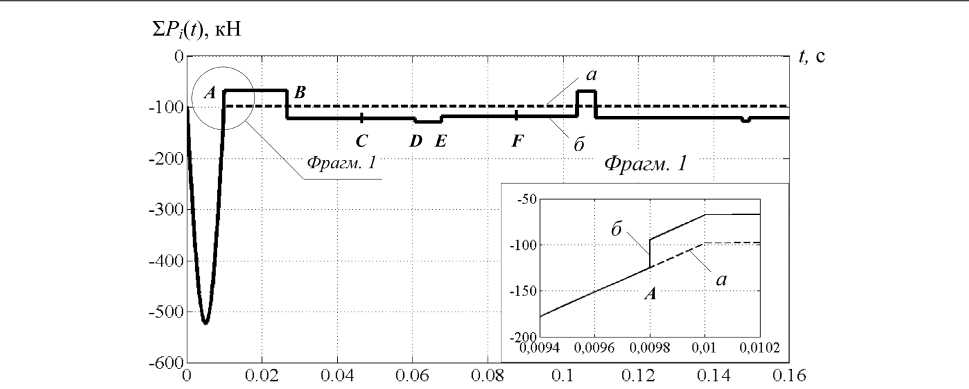
  Рис. 6. Вертикальные силы правой части уравнения (2): а – составляющая импульсной и статической нагрузок; б – полная нагрузка