Уравнение движения мелкосеменных культур в дисковом пневматическом высевающем аппарате

Целью наших исследований является математическое описание процесса взаимодействия семян с дисковым пневматическим высевающим аппаратом [2], с учётом влияющих на модель факторов – формы семенного материала, его физико – механических и технологических свойств.

Результаты и обсуждение. Теоретически исследования проведены с использованием системного анализа и синтеза [3], а также с учётом положений и методов классической механикии математики[4]. Для составления аналитических зависимостей материалом исследования являлись физико – механические и технологические свойства мелкосеменных культур. Для решения составленных уравнений, а также проверки их адекватности использовались компьютерные программы MathCAD и Excel.

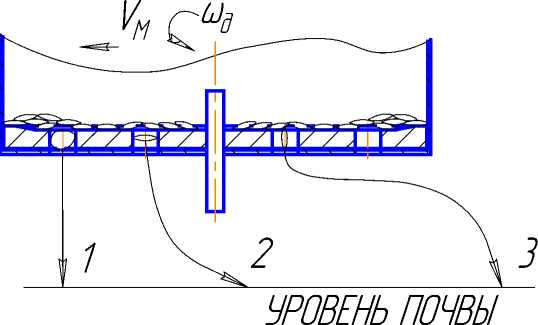
Рассматривая технологический процесс перемещения семенного материала от бункера дискового пневматического высевающего аппарата через высевные отверстия и семепровод к сошниковой группе, можно выделить три случая, два из которых являются экстремальными. Первый случай (рисунок 1), когда семенной материал 1 перемещается в сошниковую группу, находящуюся под высевающим аппаратом. При этом путь, совершаемый семенным материалом – наименьший.

• 1,    2 – траектории движения семян без влияния дополнительного воздействия; 3 – траектория движения семян с обязательным дополнительным воздействием

Рисунок – 1 -Возможные траектории движения семян в высевающем аппарате

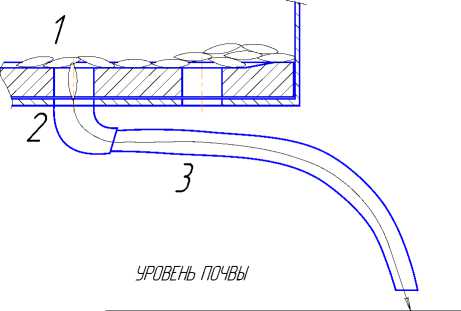
Второй случай 2 также возможен без использования дополнительного внешнего воздействия, т.е. за счёт силы тяжести семян. Однако для осуществления транспортирования на оптимальное расстояние 3 требуется применение дополнительного подталкивающего усилия. Остановимся более подробно на данном процессе. Сам технологический процесс высева семенного материала можно разделить на несколько этапов (рисунок 2):западение семян в ячейку высевного диска, выпадение семян из высевного окна в семепровод, транспортирование семян по семепроводу к сошниковой группе.

• 1    – этап западения семян в высевное окно; 2 – этап выпадения из семенного окна; 3 – этап транспортирования семян к сошнику

Рисунок –2 - Рассмотрение максимально возможной траектории движения семян по семепроводу

Рассмотрим кинематические элементы движения семян в выбранной плоской системе координат XOY [4] (рисунок 3), поскольку перемещение по оси OZ отсутствует.

Y

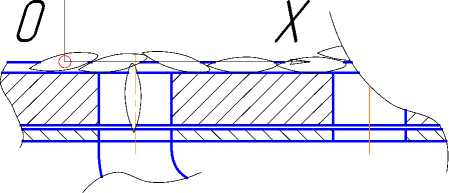
Рисунок 3 - Рассмотрение кинематических элементов движения

В таком случае координаты семян могут быть выражены

уравнением (1).

x = r • cos a;

< y = r • sin a;

z = z, 1         ,             ,                                       (1) где r– расстояние от рассматриваемой точки до начала координат;α – угол между r и осью OX.

Дифференцируя полученные координаты по времени, получим значения проекций скоростей на координатные оси и направляющие косинусы, выражаемые следующими формулами (2).

Vx dx    / = = x x ; dt * Vy dy =   = y ; dt V z dz =    = z , dt                         (2) следовательно,результирующая скорости определяется из выражения (3).

V = -

jx" + y '2 + - -'2.                   (3)

Направляющие косинусы определяются из формулы (4).

cos( V , x) =	V x =		x
	V	x 2	+ y' 2	2 ; + z
cos( V , y ) =	V y =		y
	V	x 2	2 + y	2 ; + z
c)=	V z =-		/ z
	V	x 2	+ y' 2	. 2 + z	(4)

Ускорение рассматриваемых семян определится второй производной координат и выразится следующими уравнениями (5).

ax dVx dt d2x — dtF — xH; a y — dVy dt d2y — dt2 — y ”; az dVz dt d2z — dt2" — z \ (5) откуда результирующая ускорения определяется из выражения (6).

//2        //2       //2

a — у x + У + z

А направляющие косинусы определятся из формулы (7).

_x //

cos( a, x) — —

//2

x

cos( a, y) —

// ^y

_x //2

cos( a, z) —

//

z

x //

//2

⁺ У

// ^y

+ у //2

//

z

//2 ;

+ z

//2 ;

+ z

x ^//2 + y ^//2 + z ^//2

.

Для составления дифференциальных уравнений движения, с учётом того, что на семена могут воздействовать внешние ограничения и система является несвободной механической системой, то по принципуД'Аламбера [3], можно выразить уравнение движения в декартовой системе координат в виде выражений (8).

m • x "

— Fx;

//

m • y

// m • z

— Fy;

— Fz,

где Fx – проекция приложенной силы

F на ось OX;Fy – проекция

приложенной силы F на ось OY;Fz – проекция приложенной силы F на ось OZ.

По принципу Лагранжа указанные дифференциальные уравнения в проекциях на оси обобщённых ортогональных координат можно выразить дифференциальными уравнениямивторого рода (9).

d	d T	d T
dt	' d q i	— 5 q i
d	d T	d T
dt	• 5 q 2	— 5 q г
d	d T	d T
dt	• d q 3	— a q 3

= 4;

= ^2;

= ^3,

где q1, q1, q3 – новые независимые переменные;Т – кинетическая энергия, определяемая как ^T = ^m ' V /2 ;91, 92, 93 - обобщённые силы.

Поскольку для нашего случая, рассматривая первый этап перемещения семян, движется и горизонтальная плоскость, на которой расположены сами семена, то движущей силой будет являться сила трения семян о поверхность высевного диска (силой внутреннего трения

семян, расположенных над пренебрегаем) (рисунок 4).

высевающимся семенем на данном этапе

Vc

Vд

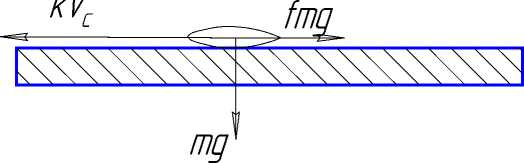
Рисунок 4 -Схема движения семян на поверхности высевного диска

Соответственно дифференциальное уравнение движения в этом случае примет вид (10).

dV

m - = f • m • g dt

,

где Vc – скорость абсолютного движения семян.

Следовательно, независимо от наличия ускорения поверхности высевного диска, предельное ускорения семян будет определено выражением (11).

a = dVc I dt = f ■ g

.

Проинтегрировав полученное выражение при начальных условиях движения (начальная скорость и пройденный путь равны нулюV0=0, S=0), можно записать значение скорости семян и пройденного пути в виде (12 и 13).

V_c = V 0 + f ■ g ■ t ;

S= = V ■ t + f ■ g ■ t c0          2

.

Принимая во внимание, что скорость движения высевного диска больше начальной скорости движения семян, а сила трения меньше силы инерции частицы, с учётом внутреннего трения семян, для превышения момента придания частице скорости движения высевного диска, семена перемещаются по равномерно ускоренному движению.

Определим время t начала движения семян при VС =VД. Используя формулу (12) подставим в неё переменную VД и выразим искомое время (14).

t = (Vд - Vo)I f ■ g

.

С учётом уравнения (13) можно записать выражение длины пройденного семенами пути до момента выравнивания скорости семян и высевного диска (15).

_s _ ^VД - ^V0

Sc=  2 fg

.

В начальный момент времени, когда скорость движения семян равна нулю, уравнение примет вид (16).

V Д

СНАЧ .    ~ r

2 f ■ g

.

Начало относительного перемещения семян, сопровождаемое перемещением элемента высевного диска описываемого уравнением (17).

S = V -t ° ДНАЧ .      Д t нач .

Vk-VA^V^ f ■ g

.

Для определения значения абсолютной скорости семян при западении их в ячейку высевного диска, подставим в уравнение (14)

значение пройденного семенами пути до момента схода с высевного диска, определив значение времени.

Предполагается, что семена прошли путь Sвып., тогда время выпадения определится формулой (18).

V 0 tВЫП -     f ■ g	2 0           ВЫП .
	( f • g )2     f • g

откуда скорость выпадения семянопределится выражением (19).

VВЫП. = V V0 + 2 " f " g ' S ВЫП.

Как видно из полученного уравнения скорости выпавших семян, особенное влияние на повышение скорости семян в момент выпадения имеет скорость движения диска и пройденный семенами путь. Соответственно, для повышения количества выпавшего сквозь ячейки высевного диска семян, требуется повышение скорости движения высевного диска.

Однако в данном случае имеется ограничение прохождения материала, что обусловлено с одной стороны расстоянием между семенами, а с другой стороны возможным сгруживанием семян в семепроводе.

В рассматриваемом процессе не учитываются факторы внешнего сопротивления воздушного потока, поскольку бункер семян закрыт.

Для рассмотрения третьего этапа – перемещения частицы по семепроводу, предположим, что начальное движение сопровождается воздействием воздушного потока, служащим для гарантированного перемещения материала без возможности образования сгруживания семенного материала в семепроводе(рисунок 5).

Скорость движения семян больше скорости внутренней поверхности семепровода, несмотря на то, что в начальный момент скорость движения семян определялась по уравнению (19).

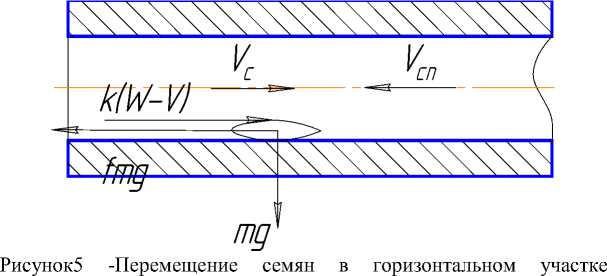
семепровода

Дифференциальное уравнение перемещения семян запишется следующим образом (20).

m   = k(W - V) - f • m • g dt                            .                (20)

Из уравнения движения можно выразить время перемещения семян:

mdV           dV

dt =----------------= -------------- k (W - V) - f • m • g   k W _ у) _ f, g

m

, а из последнего, интегрируя, можно выразить формулу (21).

t = -m ln| — • (W - у) - f • g k v m

+ C

,           (21)

где С – произвольная постоянная.

При начальном значении времени, равном нулю и определённом значении скорости V1 можно выразить произвольную постоянную по формуле

t = - m lnf— • (W - V) - f • g) + C k V m             )

, затем преобразовать уравнение (21) в вид (22).

m t = - - in

— • (W - V1) - f • g m

- • (W - V) - f • g

m

После чего можно определить скорость в данный момент времени по формуле (23).

[ k • t

k                         I -• (W - Vi)- f • g Ie m m                   v . (23)

Однако известно, что скорость является производной пути по времени, следовательно, для определения пройденного пути проинтегрируем полученное выражение и получим (24).

- k - t

I f e^ + C ₂

, (24)

.. ds              m          m ( k

V = -,7^ V = IWdt-Tf• g\dt-tI —(W-Vi)-f•g dt              k          k V m где С2 – вторая произвольная постоянная.

Соответственно, после интегрирования можно записать выражение (23) в виде (25).

k • t

| e m + C 2

. (25)

• m        m । k

s = Wt - f • g • t + г I   •(W - Vi) - f • g

• k        k V m

Анализируя данное уравнение можно получить два случая:

k

—    •(W-Vi)- f • g > 0; -    m -    • (W - Vi) - f • g < 0

m

-, из которых можно выявить, что с увеличением времени для первого случая скорость семян увеличивается до определённого предела, а во втором случае – уменьшается, но не равна нулю. Несмотря на данный факт наличие второго случая нерационально, поскольку может привести к сгруживанию семян на прямом участке семепровода.

Поскольку в семепровод семена подаются парциально, через определённые промежутки времени Δt, тогда выражение пройденного пути будет выглядеть так (26).

k • t le m -1

. (26)

(    m r ^

s a t =| ^W -    f • g l ( t ^-A t ) + тт|   ' ^{(W -} V i ) ^{- f} ' g

V    k )

Интервал пройденного пути, т.е. оптимальное расстояние между семенами в семепроводе определится разностью пройденного пути SΔtи S по формуле (27).

m   \m w - f • g Iat + 2-1   • (W - V1) - f • g k    )

k •A t       k • t

l (1 - e ^m ) e ^m

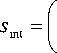
Однако прямой, горизонтальный участок семепровода имеет весьма малое расстояние, поэтому в дальнейшем рассматривается движение семян по наклонной плоскости.

Учитывая силу трения по наклонной поверхности семепровода при движении семян под действием силы тяжести (рисунок 6) и создаваемого воздушного потока, уравнение движения семян примет следующий вид (28).

d 2 s    dV

m ^ = m = m • g • sin a - f • m • g • cos a + k(W - Vc) dt        dt                                                 ,(28)

где m – масса семян;g – ускорение свободного падения;α – угол наклона семепровода относительно горизонта;f – коэффициент трения семян по семепроводу.

Тогда время для полного переноса семян к сошниковой группе определится из выражения (29).

t = m  dIc_ + c,

k  W - Vc   1

.

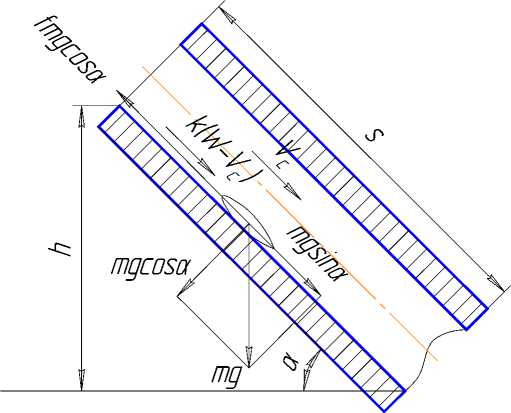
Рисунок 6 - Движение семян по наклонной плоскости

Для подтверждения составленной математической модели движения семян в дисковом пневматическом высевающем аппарате следующим этапом исследований является определение физико – механических и технологических свойств семян и дальнейшее проведение лабораторных исследований.

Выводы. Таким образом, анализ полученных уравнений, описывающих движение высевного материала показал, что на дальность транспортирования частицы в большей степени влияет наличие в воздушном потоке семян в процентном соотношении, чем и определится рассмотрение как однофазной или двухфазной среды. Также влияет создаваемое вентилятором давление воздушного потока и геометрические параметры семепровода.

Следующим этапом исследований является изготовление лабораторной установки и апробация дискового пневматического высевающего аппарата с использованием мелкосеменных культур для оптимизации параметров и режимов его работы