Уравнение нелинейной динамики световых импульсов в многомодовых световодах

УРАВНЕНИЕ НЕЛИНЕЙНОЙ ДИНАМИКИ СВЕТОВЫХ ИМПУЛЬСОВВ МНОГОМОДОВЫХ СВЕТОВОДАХ

Успехи, достигнутые в применении нелинейных свойств одномодовых световодов [l], привели к необходимости обобщения уравнений, описывающих распространение и взаимодействие световых импульсов, на случай многомодовых световодов (МС). С этой целью в [2] было предложено использовать обобщенное нелинейное уравнение Шредингера, в котором учитывается изменение показателя преломления, пропорциональное суммарной интенсивности полей мод. В [3,^] на основе теории связанных мод уда лось получить более полное описание нелинейных эффектов, соответствующих прони- цаемости 6^5^

+ со - со ) . Результаты этих работ были получены в прибли-m п жении слабонаправляющих световодов, а учет поляризационных эффектов сводился к рассмотрению двух крайних случаев - деполяризационного и линейно-поляризационного излучения. В настоящей работе вышеуказанные приближения не использовались, но учитывались возможные нерегулярности структуры световодов, а также наличие мод излучения. При выводе уравнений нелинейной динамики световых импульсов в МС впервые получен полный набор нелинейных членов, связанных с нелинейной проницаемостью третьего порядка. Это позволило классифицировать нелинейные эффекты, протекающие в МС, по виду нелинейных членов традиционным способом.

Далее будем исходить из следующей связи между Е и D:

D(w) = ё(ы)Е(ш) + е1 (ш)Е(со) + Онл(ы),                                          (1)

е (со) - диэлектрическая проницаемость регулярного световода;

е1(ш)  - возмущение диэлектрической проницаемости, связанное с нерегуляр ностью ;

"*нл                                   "*

D (со) - нелинейная часть 0(ш).

Предполагается, что волновод изготовлен из изотропного материала. Как известно [5], в изотропных средах отличная от нуля нелинейность наименьшего порядка описывается членами, кубичными по Е:

0д3> (ш) = /е^^ (ш1 ,со2 ,<о-со1-со2) Е^ (со1) Е^ (<о2) Е^ (<о-<о1-<о2) dco1 dco2 ,

Где ea0Y6

тензор нелинейной проницаемости третьего порядка,

и по индексам ф,у,6

подразумевается суммирование. Пренебрегая членами высших порядков, будем считать, что Внл(щ) = D <3* (о), IDHл(o)l « ID(о) I. Все величины в формулах (1), (2) являются функциями о и координат г = (x,y,z), причем ось световода считается направ

ленной вдоль оси z. Опуская далее аргумент о и полагая, что магнитная проницае

мость ц = ц0, запишем уравнение Максвелла (в системе MKS)

rot rot которые

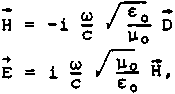
div Н = О, div D = О, совместно с (1) ,

(2) составляют замкнутую систему для нахождения полей

возмущенного световода.

Ортонормированность и полнота набора поперечных составляющих полей мод регулярного световода е^(х,у) позволяют представить Е в виде разложений [6]

Bt = £(bk(z)?kt + Z bk(z,Q)®kt(Q)dQ1 для поперечной (индекс t) и

(4а)

^Ez ⁼ =" ^^{bk^(z)ekz ⁺ "о ^bk^(z'^Q)ekz^(Q)dQ)

продольной (индекс z) компоненты.

Суммирование ведется по вперед- (к > 0) и назад- (к < 0) распространяющимся

направляемым модам и модам излучения.

Повторяя основанный на теореме взаимности вывод уравнений связанных мод [6]

с учетом нелинейного члена в формуле (1), получим:

—^ - ip.b. = iS (c..b. + 7 с (Q)b. (Q)dQ) + id™ , dZ         J J ^         А о             a-                 J

где Bj

- постоянная распространения j-й моды,

с -к (z) = sign (j)     / ^ / e (r) (e‘ • e ’ )dA представляет собой коэффициент связи мод на нерегулярности, а н л                  гчг d. = sign (j)     / -^ / (е? • D™)dA

учитывает нестационарное возмущение световода, обусловленное нелинейностью сре

ды. В формулах (6), (7) интегрирование ведется по поперечной плоскости А, штрих означает, что z - компонента взята с множителем е/(ё+е ) из формулы (4б). Выражение для Cjk(t,Q) получается при подстановке в формулу (6) e^tQ) вместо ек.

Осуществим переход к временному представлению, используя приближение "мед

ленных амплитуд , согласно которому функция^ (со) отлична от нуля в узком ральном интервале Дш^ вокруг точек IcOj , где где u)j - несущая частота j-й моды и

Део j « со ^ .

Неравенство (8) дает возможность пренебречь изменением структуры мод

спект-

в пре

делах спектральной ширины импульса,

Bej (со) Эсо

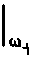
Дсо^

|"j 4<о

и позволяет выполнить переход к временному представлению с помощью обратного преобразования Фурье разложений (^а,б) следующим образом:

- _                  КР.г-ш. t) .

E(r,t) = Е (ф. (z,t)e ке' + кк

„             1 (fL (Q) z-w. t)-(ю)

+ / Фк(2,Ь,0)е к к ek(Q)dQ) + к.с., где

Фк(г,Ъ) = е { bk(z,co)e la)cdm(11)

является медленно меняющейся амплитудой

|э? « ^к'*1^1' Ы « “к^к1-

Формула (10) выражает решение задачи о нахождении электромагнитного поля возмущенного световода через амплитуды Фк<г,Ъ). Уравнения для них могут быть получены с помощью обратного преобразования Фурье системы (5). Выполнив интегрирование по положительным со (область со < 0 даст комплексно-сопряженный результат) с учетом дисперсии до второго порядка включительно, в левой части уравнений получим

i(0.z-a>.t) _          K^z-o-jt) 4 Эафч        Зфл Эфл le =  1 L3 ф, - 1=  1 ЩЗ ^- 11^ ^ * ^» ,

ИМ

1 aeuco) 1       .    , э2злш) I где U1 - Эш Lj' U2 - 2 Эш2 lead

В правой части получим члены, связанные с нерегулярностью 1(Вкг-шкЪ)                     ,

^ cjk е         Фк' 8jk = ^к^Чш/ и члены, связанные с нелинейностью i Е К^ (±ш. , ±ш , ±шп)е         ' Фк Ф Ф .

.        тп к т п              к т п к ,т, п где

В = ^к ±Вт ±8п' П = ±Шк ~шт ±ton' Rin(±Uk' ^пА1 =

= sign(j) D ®^П) /^ , e^do^, ±шт, ±шп) е‘а (О) е^*’ е^**’ е^‘> dA, причем по индексам а,0,у,6 подразумевается суммирование. При выводе выражения (15) использовались соотношения (7), (2), (4а, б), (11). Суммирование нелинейных членов (15) ведется по всем комбинациям знаков частот, удовлетворяющим условию П > О (6(Q) = 0, при П < 0 и в(П) = 1, при П > 0), и всем вперед- и назадбегу- щим модам. Знак комплексного сопряжения в скобках означает, что сопряжение про изводится в тех случаях, когда частота, со знаком "-".

тп

Влияние мод излучения на эволюцию ф^ регулярностью, описывается суммой

соответствующая данной моде, входит

(z,t) для возмущений, обусловленных

в

не-

.          i(3. (Q)z-w. t)

IE / с.. (Q)e к к ф. (Q)dQ k о jx                        к

а для нелинейных возмущений - суммой членов вида:

7 R3k(Q)ei(B(Q)z-Qt) ф'*’ (О^Ф**' dQ,(17)

о mn                   кш и Ао,»'!.116™'0'11-011 ф"’ <о)ф"' (Оф-^аоао'"”

оо mn                            *

777 R^(Q,Q' ,Q")e1(B(Q,Q' 'Q")z-Qt) ф,*) (0)ф**' (Q* )ф‘** (Q")dQdQ'dQ" ООО                                                  К         IP.n так, чтобы конечные выражения были симметричны по индексам k,m,n.

и В определены согласно формулам распространения В и собственные

В выражениях (16)-(19) величины С^, R^ (1^)» (15), в которые подставлены постоянные поля е соответствующих мод излучения. Обычно из-за сильного затухания амплитуды мод излучения существенно меньше амплитуд направляемых мод, и в первом приближении можно ограничиться членами (16), (17), линейными по амплитудам мод излу чения .

Сравнение левых (13) и правых (14), (15) частей эволюционных уравнений показывает, что для эффективного протекания процессов нелинейного взаимодействия мод необходимо выполнение условий:

П - О) . = Дй) « О) . , -3              3

В - Bj = дв « By

В случае выполнения неравенств (20),

Lj Ф3

. i(Bv~B4)z -i (ox-w. )t

Е с., е k 3 е К 3

к зк

(21) получаем окончательно

Фк +

...               КдВг-доб)

♦ Е В3^(±шк,±ш,±ы)е          ф.^’ф^’Ф'*’

«        mn к m n                  х m п / к ,m, п где

Lj = u>^' 1;                                    ('

Sjk = Si9n <7> £ ^ ' е^Не*. • ^dA^;(24)

О^'^т'^г? " si9n(j)^ ^ ' ^б^'^т'^^аЧе*’^

Для краткости в уравнения (22) не включены члены (16)—(19) , учитывающие влияние мод излучения. Эволюционные уравнения для них имеют аналогичную форму.

Обсудим полученные результаты. В левой части уравнений стоит дифференциальный оператор L., учитывающий дисперсионные свойства среды, в которой происходит распространение и взаимодействие световых импульсов. Эти свойства определяются совокупностью материальной, волноводной и межмодовой дисперсий . В стационарном случае, когда ф.(г,Ъ) = ф.(г), оператор L. сводится к .

3                3                          3                     ° г

Такое упрощение связано с переходом от волновых пакетов с конечной спектральной шириной Део,, к волновым полям с дискретным спектром. Правая часть уравнений (22) дает возможность определить влияние на эволюцию импульсов нерегулярностей световода и нелинейности среды. Взаимодействие мод на нерегулярностях эффективно лишь при совпадении их несущих частот. Это условие, вытекающее из уравнений (22), представляется естественным следствием стационарности возмущений, связанных с нерегулярностями.

— 9Я -

Сумма нелинейных членов эволюционных уравнений (22) имеет вид, характерный для общего описания четырехволновых процессов в однородных средах с условиями фазового синхронизма са- = tea, tea

(26а)

-3     _к   m п р. = te, te te

3       к         п

Благодаря этому можно провести обычную классификацию нелинейных эф- фектов в МС , связанных с нелинейной проницаемостью е^^^са^ = е(?’ (са. = tea, tea tea ) , роль которой в уравнениях (22) играет аруо 3 к m п tca„ tea )

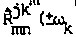
= RJ (са. = lea, tea tea ). К примеру, генерация третьей гармоники в mn j k m n*qk                     з описывается членами R^ (са^ = <а^ + са^ + ш^)ф^; процессы, в которых накачки в модах k, m рождаются волны в модах n, j

световодах

из двух волн

членами

R^k(ca. = са, +са - са ) ф, Ф Ф*; одночастотные эффекты mn j k m n к m n вида R^ (ш = ш + а)-со)ф.ф ф*, обращение волнового mm               i m m

^2^_j (^ = ш + са - са)ф^ф^ф^j. Отметим, что до сих пор

самовоздействия - членами

фронта

членами вида

в работах, посвященных полу

чению эволюционных уравнений для МС, учитывались лишь члены вида:

(са . = са . + са — о )ф.ф ф* и (о. = са, + са - са ) ф, Ф ф* Г 2—41 .

mm' з з m m'*j*m^vm mn' j         m n'*k*m^vn ^{L J}

Эффективное протекание нелинейных процессов при распространении и взаимодействии световых волн возможно при выполнении условий синхронизма (2ба,б>. За исключением случаев, в которых эти условия выполняются автоматически (напри-

мер, для самовоздействия импульсов

по сравнению с однородными средами

за счет компенсации материальной и

и обращения волнового фронта) в световодах больше возможностей для их удовлетворения волноводной дисперсии - межмодовой. 8 одно- родных средах для этой цели приходится использовать неколлинеарные процессы, что снижает их эффективность из-за малой длины взаимодействия. Кроме того, в световодах возможны эффекты, не имеющие аналога в однородных изотропных средах из-за невозможности выполнения условий синхронизма даже при неколлинеарном взаимодействии. Таким эффектом может быть нелинейное одночастотное возбуждение мод, описываемое членом RJ (со = со + ш - са) • Ф^Ф„Ф„ при таком подборе параметров mn                  к m п

(V»)

световода, что выполняется условие Р^ (ы) = Р^ (со) + Вт(ш)

Нетрудно убедиться, что в бездиссипативных средах при выполнении условия синхронизма (26а) и отсутствии нерегулярностей система (22) допускает выполнение закона сохранения энергии:

где

Е Е j (Z)

const

Ej

Е .

(Z )

sign(j) • / |Ф^ sign(j)| ф ^(z)|2

(z,t)| dt для импульсов и

для монохроматических волн.

Кроме

выполняются

соотношения Мэнли-Роу. Например, для эффектов, свя-

занных

с Rjk mn

“j

dEj dz

(Oj = (^ 1 dEn

0) m

п

coj^ dz

эти соотношения имеют вид:

’ dEm

Шт dz

соответствующий процессу, в котором фотоны в модах j и п рождаются, а в модах кит поглощаются (или наоборот).

Кроме процессов взаимодействия мод, обусловленных отдельно нерегулярностью и нелинейностью световодов, на основе (22) могут исследоваться эффекты, в которых становится важным их совместное проявление. Таким эффектом может быть, например, самовоздействие световых импульсов в периодически нерегулярной среде [7].

Другим интересным случаем является проявление самофокусировки в статисти-чески-нерегулярных световодах с большим числом мод.

Если нелинейные взаимодействия поля со средой сопровождаются диссипацией, то уравнения (22) могут применяться для описания таких эффектов, как ВКР , двухфотонное поглощение и других, связанных с мнимой частью нелинейной восприимчивости .