Уравнение Пуассона в решении задач электродинамики сплошных сред

На данный момент теоретическая физика нуждается в наличии решений уравнений математической физики для различных условий, так для результатов экспериментов, проводимых в настоящее время, требуется теоретическое описание. Оно создаётся с помощью общих математических моделей, математическое описание которых уже известно.

Существует множество уравнений, с помощью которых атематическая физика описывает физические процессы. Все они делятся на три типа: гиперболические, параболические и эллиптические. Мы остановимся на уравнении эллиптического типа, а именно на уравнении Пуассона:

A u = f ( x , y ) , где u – искомая функция.

Данное уравнение используется в различных областях физики, например, электродинамике сплошных сред. Рассмотрим уравнение Пуассона для диэлектрического шара в электрическом поле:

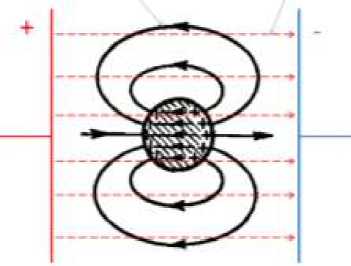
Рис.1. Картина силовых линий.

div£(r)gradф(r) = —4np, r- расстояние от центра шара, ф- потенциал шара, р - объёмная плотность заряда.

£ 1 , 0 < R     „

£(r) = i         , где R - радиус шара.

£ 2 , r > R

Граничные условия:

φ 1 (R, θ)= φ 2 (R, θ)

• _-   ∂φ 1   _{= -} ∂φ 2

• ¹    ∂r _R       ² ∂r _R ^.

Общее решение:

∞

φj(r, θ) = ∑ [A(lj)rl + Bl(j) l+1] Plcosθ, l=1

С учетом граничных условий:

r > R, 0 ≤ θ ≤ π.

φ1(r, θ) = 3E0ε2 rcosθ, r < R.

(ε₁ - ε₂)      cosθ

φ2(r,θ) = - E0rcosθ +           E0R3     .

Рассмотрим модель шара:

£ внутр ( r ) = £1( r ) + £2( r )•

£1( r ) = e - r 2 ,

£2( r) = "Г•

r

Далее начнём решать уравнение Пуассона:

² e div £ (r ) = (—

—,

r z x      4

div £ ( r ) = —-• r

■ r 2

--2 re ^{— r 2} ),

Для первого потенциала внутри шара:

(

2 e

- r ²

^-

r

2 re  ) divgrad ^ ( r , 0~) = 0.

^ ( r , 0 ) * - A_x ⁽¹⁾ r cos 0 , r = 1.

^ ( r , 0 ) = - A ⁽¹⁾ r cos 0 , r * 1.

⁽ e

—

r

^ (r, 0) = — Eor cos 0 + Eor----

— r ²

e

4 r3

r

)

Для второго потенциала внутри шара:

12 ,       ,   ,        A

- — divgrad^ ( r , 0 ) = 0.

r

^ (r, 0) * — B!(1)r cos 0, r = 0.

^ (r, 0) = — B!(1) r cos 0, r * 0.

⁽ e

— r

, 2

^ ( r , 0 ) = — E_or cos 0 + E_or —

e

— r ²

r3

r

)

С помощью рассмотренных решений можно давать теоритическое описание различным физическим явлениям или предсказать их. Например, реакция с трёхмерной диффузией в шаровой области.

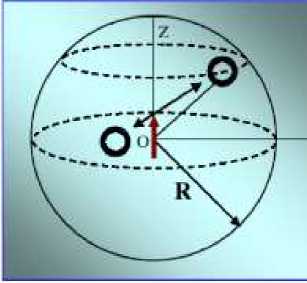
Рис.2. Шаровая нанообласть диффузии-аннигиляции частиц объёмом VR c отражающей поверхностью – сферой SR.

⎪⎧

G(r, θ, t) =

4πR3

к

(0)   _,

∑^∞ exp[-^D(μ⁽⁰⁾)²t] ^{J 1 2( R} r_{)J 1 2(} μ⁽ n _R⁰⁾r , ) n=1         ^{R k}       2πR²√rr^,J₁² ⁄ ₂J 1 (μ⁽_n⁰⁾)

(0) ^μ n ^r

■> +

⎪⎬

• (l)                (l)  ,

  ∞

  + ∑ exp [- _R (μ⁽_n^l)) t]

  n,l=1

  
  

J_l+ 1 (^μk_R^r)J_l+ 1 (^μk_R^r)(2l + 1)

Plcos.

l ² +1⁄2 J 1 (μ⁽_k^l))[1+l(l-1)⁄(μ⁽ n ^l))²]

Также можно описывать модели экспериментов с использованием серебряных наночастиц, углеродных нанотрубок, но для последних необходимо преобразовывать уравнение Пуассона для цилиндрической системы координат.