Уравнения движения одиночного заряда в вакууме

Рассматривается движение одиночного электрического заряда в вакууме при отсутствии каких-либо электромагнитных полей. Решается система уравнений Максвелла для этого случая и показывается, что электрический заряд, обладающий кинетической энергией, движется в вакууме по спиральной траектории с замедлением, вызванным затратой энергии на перемагничивание окружающего пространства.

Рассмотрим одиночный заряд, движущийся в вакууме, где отсутствуют какие-либо электромагнитные поля. Такой заряд движется прямолинейно с постоянной скоростью. Известно, что такой заряд не излучает электромагнитных волн и не расходует на этот процесс энергию. Однако вокруг него создается магнитное поле, которое формируется заново в каждом новом положении заряда. Этот процесс требует затрат энергии. Действительно, предположим, что заряд движется около тела, изготовленного из магнитно-мягкого материала. Изменения магнитного поля в нем вызывает перемагничивание материала, на что расходуется энергия. Эта энергия была затрачена движущимся зарядом. Следовательно, энергия для перестройки магнитного поля расходуется движущимся зарядом всегда . Исходя из этой предпосылки, рассмотрим математическую модель движения одиночного заряда в вакууме.

Прежде всего рассмотрим систему уравнений Максвелла для такого заряда. Следуя Эйхенвальду [1], движение заряда q 5 со скоростью U можно считать эквивалентным электрическому току

I = qv.                                 (1)

Тогда это движение описывается так же, как постоянный ток – см. приложение. Это означает, что заряд не может двигаться строго линейно, а движется по спирали . Вместе с зарядом движется поток энергии, равной в данном случае кинетической энергии заряда.

Этому потоку энергии соответствует объемная плотность силы Лоренца,

F = a                        (3)

где ц, p - абсолютная магнитная проницаемость и удельное сопротивление движению заряда. Его происхождение будет показано ниже.

Эта сила действует на заряды в теле провода. В нашем случае поток энергии движется вместе с зарядом, а сила Лоренца действует на этот заряд. Поток энергии, как известно, равен мощности. Следовательно, мощность движения заряда

Р = Sb,                             (4)

где b - площадь поперечного сечения заряда. С другой стороны, известно, что мощность — это

(б)

(ба)

Р = FVv, где V - объем заряда. Из (3, 4, 5) находим: р = SyvV pb или

V = ^

pV где ц, p - абсолютная магнитная проницаемость вакуума и удельное электрическое сопротивление движению заряда. Это сопротивление вызвано тем, что заряд тратит энергию на переформирование электрического поля. С третьей стороны известно, что мощность

Р = pl2.

Из (1, 6, 7) находим:

SpvV      , _Л2

-pb" = Р(Ч”).

Следовательно,

Наконец, мощность Р - это мощность, с которой расходуется кинетическая энергия заряда, т.е.

Р = mva,(10)

где т,а - масса и ускорение заряда. Из (5, 10, 3, 6а) находим:

= FVv = Spv = Sp pb = Sb, m mp mp pV mV"

Таким образом, электрический заряд, обладающий кинетической энергией, движется в вакууме по спиральной траектории с замедлением, вызванным затратой энергии на перемагничивание окружающего пространства .

Приложение. Математическая модель постоянного тока

(краткое изложение по [2])

При моделировании будем использовать цилиндрические координаты г, р, z в системе СИ.

Уравнения Максвелла для провода постоянного тока имеют вид:

rot(7) = 0 ,                                                         (а)

rot(H) -J-J_o = 0 ,                                    (b)

div(J) = 0 ,                                                         (с)

div(H) = 0 ,                                                    (d)

где

• основной ток с плотностью /₀, передаваемый по проводу в

нагрузку, •    дополнительные токи с плотностью J = (/г,/ф,/z), •    магнитные напряженности H = ( нг, H ^ , Hz ) ,
Уравнения (a-d) для цилиндрических координат имеют вид:
н т , ЭН , 1 . дН ф , ЭН = 0 г    Эг г Эф    Эz     ’	см. (d)	(1)
1 ЭH z ЭН ф = . г Эф    Эz Гт '	см. (b)	(2)
ЭН  9HZ —_— = Jф '	см. (b)	(3)
Н ф + Э2Н ± _ 1 . ЭН г = , . , г Эг г Эф zz о	см. (b)	(4)
J r ,   Э ) г  , 1   Э ) ф  . Э /z __ 0 г    Эг   г  Эф    Эz     ’	см. (с)	(5)
1 ЭА   ЭJф   0 г Эф    Эz     ,	см. (a)	(б)
ЭJr    ЭJZ   0 Эz Эг      ,	см. (a)	(7)
Jф + Э2 ф _ 1 . Эк = 0 г    Эг г Эф     "	см. (a)	(8)
Для сокращения записи в дальнейшем	будем применять
следующие обозначения:
co = cos( ар + xz) ,		(10)
si = sin( ар + xz) ,		(11)

где а, X — некоторые константы. Для этих уравнений существует решение, которое имеет следующий вид:

/г = Jr СО,(12)

J

Jz = Jz si,

Нг = hr co,(15)

^H p    ^h p si ,                                           (16)

H_z = h z si,                                          (17)

где j⁽r), h(r) - известные функции координаты r . При данном r все токи и магнитные напряженности оказываются на винтовых линиях. На рис. 1 показаны три винтовые линии, описываемые функциями (10, 11) тока с проекциями /_р и j_z при r = const . Эти проекции определяются по (13, 14), т.е. зависят от функции si. На рис. 1 показаны: толстая линия при а = 2,/ = 0.8, средняя линия при а = 0.5, х = 2 и тонкая линия при а = 2, / = 1.6 .

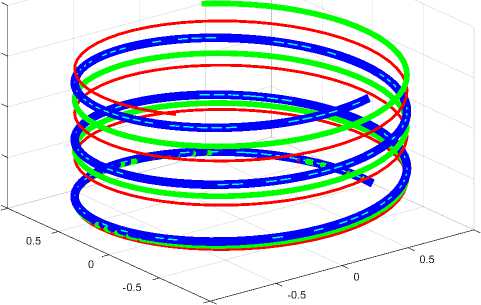
Fig. 1.

(TokPotok33.m)

-1        -1

Плотность потока электромагнитной энергии — вектор Пойнтинга определяется в этом случае по формуле:

5 = Е х H.(18)

Токам соответствуют одноименные электрические напряженности, т.е.

Е = p-j,(19

где р - удельное электросопротивление. Совмещая (18,19), получаем:

S = pj х H = ^j х В.(20)

Магнитная сила Лоренца, действующая на все заряды проводника в единичном объеме - объемная плотность силы Лоренца равна

F = j х В.(21)

Из (20, 21) находим:

F = ц5/р.(22)

Следовательно, в проводе с постоянным током плотность магнитной силы Лоренца пропорциональна вектору Пойнтинга .

Итак, ток с плотностью J создает поток энергии с плотностью S, который тождественен магнитной силе Лоренца с плотностью F. Эта сила Лоренца действует на заряды, движущиеся в токе /, в направлении этого тока. Следовательно, можно утверждать, что вектор Пойнтинга создает э.д.с. в проводнике.

В цилиндрических координатах плотность потока электромагнитной энергии (3) имеет три компоненты S_r , S ф ,S_z,

направленные вдоль	радиуса, по окружности, вдоль	оси
соответственно: [ Srl	1" J ф Н z - C/ z + J о )Н ф 1 pC/ х Н) = pl / z Hr-/rH z + / о Н 1 . [/г Н ф -/ ф Н г + J г Н оф\
S = 5 Ф =		(23)
[ Sz]
где НО ф = ]ОГ .		(24)

Итак, в проводе циркулируют потоки электромагнитной энергии . Они являются внутренними. Они порождаются токами и магнитными напряженностями, создаваемые этими токами. В свою очередь, эти потоки воздействует на токи, как силы Лоренца. При этом суммарная энергия этих потоков частично расходуется на тепловые потери, но в основном передается в нагрузку.

Продольный поток энергии S_z . равен мощности Р , передаваемой по проводу:

Р = Sz.                                                 (25)

Эта мощность изменяется вдоль провода, т.к. часть энергии тратится на тепловые потери. При известном потоке энергии и геометрических размерах провода могут быть найдены значения констант а, % .

Таким образом, показано, что существует такое решение уравнений Максвелла для провода с постоянным током, которому соответствует представление о

• •    законе сохранения энергии,

• •    винтовой траектории постоянного тока в проводе,

• •    передаче энергии вдоль и внутри провода,

• •    зависимости плотности винтовой траектории от передаваемой мощности.