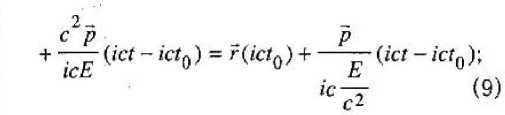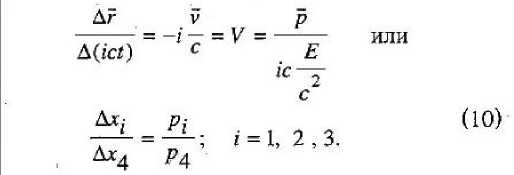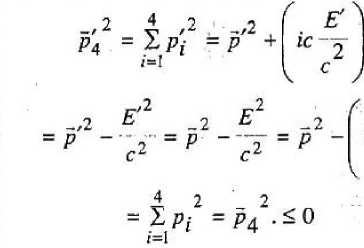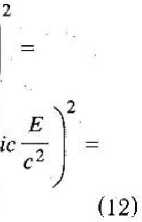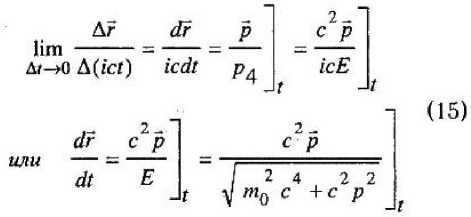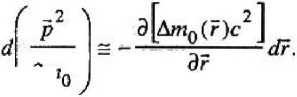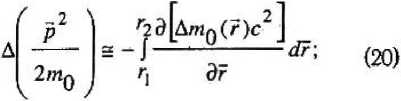Уравнения Гамильтона в релятивистской механике классической материальной точки в приближении малых импульсов
Автор: Федоткин А.Н.
Журнал: Инженерные технологии и системы @vestnik-mrsu
Рубрика: Теоретическая физика
Статья в выпуске: 3, 2007 года.
Бесплатный доступ
Короткий адрес: https://sciup.org/14718896
IDR: 14718896
Текст статьи Уравнения Гамильтона в релятивистской механике классической материальной точки в приближении малых импульсов
Вторая половина прошедшего столетия ознаменовалась необычайным прогрессом физики элементарных частиц, в рамках которой была создана так называемая стандартная модель релятивистской квантовой калибровочной теории поля, подчиняющейся принципам инвариантности. Эти принципы требуют, чтобы взаимодействия между фермионами (образующими семейства кварков и лептонов) переносились с помощью особых калибровочных бозонов (глюонов, фотонов, гравитонов, промежуточных слабых бозонов). Существенно новым шагом в этом прогрессе явилось то, что впервые физики смогли вывести лагранжиан взаимодействия (сильного, электрослабого), который ранее даже в самых «продвинутых» теориях квантованных полей только постулировался [1].
В свете этих достижений кажется огромным тот казавшийся недавно непреодолимым разрыв, который образовался между новой физикой и представлениями о предмете механики, складывавшимися в течение последних трех столетий в рамках так называемой ньютоновской версии классической механики. Первым шагом на пути преодоления этого разрыва является переосмысление с точки зрения эйшн-штейновской специальной теории относительности [4] основ механики классических материальных точек, вершиной которой являются уравнения Гамильтона [2]. Однако это переосмысление должно быть результатом не просто пересмотра пространственно-временных отношений при построении непротиворечивой «электродинамики движущихся сплошных сред». При релятивистском подходе к основам именно механики должны изначально учитываться те особенности поведения и эмпирически обнаруженные ограничения в поведении материальных точек любой природы, которые регистрируются современными средствами экспериментальной физики и,в частности,в поведении электрически нейтральных микрочастиц. Первым в ряду фундаментальных ограничений такого рода следует признать существование предельной скорости движения любых механических объектов. В этом отношении современная квантовая электродинамика «включается» в мир материальных тел в том плане, что она постулирует существование особых ультраре-лятивистских микрочастиц (фотонов), которые существуют только как движущиеся переносчики импульса и энергии, причем преодолевают пространственные расстояния от места «рождения» до места «уничтожения» с предельной скоростью («скоростью света») независимо от того, на какое расстояние, какой импульс и какую энергию они при этом переносят.
Под релятивистской классической матераль-ной точкой понимается любой материальный объект, собственными размерами которого можно пренебрегать на любых сколь угодно малых расстояниях от этого точечного объекта, но при этом он является корпускулярным носителем массы, импульса и энергии в том смысле, что в каждый момент времени занимает вполне определенное место («точку») в пространстве и с течением времени непрерывным образом преодолевает цепь пространственных положений, образующую траекторию движения; к тому же, находясь под любыми внешними воздействия-
ВЕСТНИК Мордовского университета | 2007 | № 3
ми, этот точечный объект не испытывает никаких трансмутаций, сохраняя неизменной свою индивидуальность.
Теоретическим выражением детерминированного непрерывного поведения любой совокупности величин (х„х„, .... х ), по тем или иным соображениям объединенных в систему х, является формула предсказания значения «вектора» х(/) в любой момент будущего времени t > ty если известно его значение в настоящий момент времени t0~ xlt) и если существует, имеет конечное и единственное значение в каждый момент времени производная этого вектора по времени:
Jim Дх
Тогда значение вектора я в момент времени t > ^ будущего может быть предвычислено по формуле:
x(r) = ^, + J ^ di' = ^ + f vVV- (2) * di ;
Здесь o(f) представляет собой предполагаемый, подлежащий еще только определению, временной ход производной в интервале от момента tQ до момента предсказания I. Чтобы его выявить, мы можем воспользоваться тем же принципом экстраполяции, если только окажется, что производные соответствующих порядков также существуют, непрерывны и однозначны в каждый момент времени, В результате многократного применения процедуры предсакзания производных все более высоких порядков мы в итоге получаем экстраполяционную формулу для будущего положения материальной точки в виде известного ряда Тейлора со специфической формой остаточного члена:
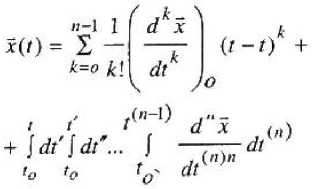
Для материальной точки, положение которой в пространстве однозначно определяется тремя декартовыми составляющими радиус-вектора г = (х, у, z), природа движения оказалась такой, что кинематика любого движения полностью исчерпывается временным поведением ускорения тела, причем последнее предопределяется целиком внешними воздействиями, обуславливающими так называемую силу, которая, в свою очередь, вызывает ускорение обратно пропорциональное универсальной (независимой от природы сил) механической характеристике тел — массе т:
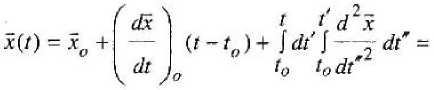
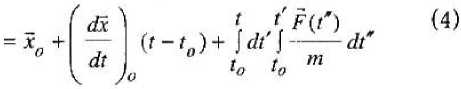
Поскольку в отсутствии внешнего воздействия сила F ~ О, отсюда следует, что движение тела должно носить прямолинейный и равномерный характер. Это обстоятельство фундаментальным образом ставит вопрос о системе отсчета, в которой уединенные материальные точки движутся прямолинейно и равномерно и как частный случай — покоятся. Классическая механика просто постулирует существование подобных так называемых инерциальных систем отсчета (ИСО), не уточняя причину того, почему одни уединенные тела в ИСО покоятся, другие движутся по инерции, причем с различными скоростями.
Можно показать, что еще на стадии анали за причин инерциального движения мы приходим к фундаментальным динамическим понятиям импульса и энергии и к истинному пониманию релятивистской природы их взаимной связи, выражаемой известным дисперсионным соотношением.
При новом подходе в первую очередь конкретизируется модель, в рамках которой формируется понятие об инерциальных системах отсчета и которая определяется как мир механических объектов в виде совокупности уединенных нейтральных материальных точек с детерминированным поведением. Наблюдатель, находясь на одном из этих объектов, обнаруживает, что его окружают две категории тел, составляющих остальной мир этого рода тел. Одна из них включает все те тела, которые находятся ни отношению к телу отсчета и между собой в неизменных взаимных положениях. Эти покоящиеся тела и служат ориентирами (вехами) для определения пространственных местоположений событий, которые состоят из совпадений, испытываемых всеми остальными телами, составляющими вторую категорию из так называемых инерциально движущихся тел.
Изучение протоколов регистрации положений и времени совпадений, сопровождающих бытие нерциально движущегося тела, приводит к выводу, что это прямолинейное движение имеет во времени равномерный характер. Поэтому кинематической характеристикой инерциального движения является темп или скорость прямолинейного равномерного движения v — путь, проходимый, таким образом, за единицу времени. Эмпирическое изучение скоростей, встречающихся в обсуждаемом мире тел, показывает, что, имея произвольные направления, эти скорости по величине оказываются в пределах от нулевых значений — для покоящихся тел — до значений, сколь угодно близких к скорости фотонов («скорости света»), которая является предельной для распространения любых взаимодействий в природе. Резюмируя все вышесказанное, можем утверждать, что мир уединенных тел указанного рода подчиняется следующему кинематическому закону инерциального движения:
г (г) = ^ + v(r — z0), (5) что как раз отвечает первым слагаемым в формуле (4) для случая F = 0. Но так как теперь в экстраполяционной формуле имеем дело со случаем постоянства первой производной, естественным образом возникает вопрос: что отличает покоящееся тело от инерциально движущегося тела того же рода и в чем причина того, что одни уединеннные тела имеют одну скорость, другие, возможно, такие же по природе — другую? Ответы могут быть получены только эмпирически, например, при изучении явлений удара, когда тело, находящееся в покое, мгновенно переводится в состояние инерциального движения или, наоброт, движущееся тело полностью останавливается. При этом выясняется, что в результате удара тело получает некий импульс, под действием которого тело приобретает скорость, зависящую, как казалось со времен Ньютона, только от массы тела:
Аг р
—(6) At т
Однако этот закон динамики инерциального движения на самом деле верен лишь для сравнительно малых значений импульса (или для больших масс), ибо при больших импульсах скорость неограниченно растет, тогда как в дей ствительности (например, в микромире) она стремится к предельной величине с. Путем подбора подходящей эмпирической формулы мы находим таковую в форме
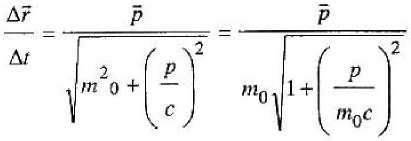
Здесь масса, фигурирующая в (6), заменена на массу покоя т0, поскольку ее значение отвечает предельному значению при импульсе, стремящемся к нулю. Но при более тщательном анализе следствий, вытекающих из этой формулы закона, выясняется, что на самом деле закон должен иметь вид:
„ 2 2 _
Аг ср ср
М 4 2 2 £ (8)
ш уто с +с р с где так же на эмпирическом основании выявляется новая динамическая величина Е — энергия, присущая как покоящемуся, так и движущемуся инерциально телу. Но решающим аргументом в пользу эмпирической формулы является ее релятивистская ковариантность. В рамках нашей модели мира уединенных классических материальных точек множественность инерциальных систем отсчета следует из того, что при переносе начала отсчета в другую инерциально движущуюся материальную точку остальной мир так же будет делиться на две категории тел: покоящихся относительно нового тела отсчета и инерциально движущихся. Свободные от противоречий и парадоксов формулы перехода из одной ИСО в другую известны как преобразования Лоренца [4]. Связи между событиями, сопровождающими движение тел, с точки зрения различных инерциальных систем отсчета особенно просто выражаются на геометризованном языке 4-пространства Минковского [3], в котором к трем пространственным координатам г = (х, у, z) события присоединяется мнимая ось времени tT; на оси времени откладывается длина пути, который проходит за время по часам данной ИСО О эта последняя по отношению к любым другим ИСО О', относительно которых она движется со скоростью, сколь угодно близкой к скорости света. В этом пространстве импульс р и энергия £ оказываются составля- юшими 4-импульса р4 = (р, 1сЕ/с2), квадрат длины которого является релятивистским инвариантом. Мировая линия инерциально движущегося тела в любой ИСО представляется в виде прямой линии, продуцируемой неизменным 4-импульсом тела
V — r^ict) = r(ict()') + — Таким образом выясняется, что закон динамики инерциального движения (8), выраженный через мнимую скорость V = -I и/с, имеет вид: Этот результат можно рассматривать как теоретическое подтверждение адекватности природе полученной эмпирическим путем формулы (8). А окончательная четырехмерная форма экстраполяционной формулы для инерциально движущегося тела может быть представлена в виде: \О4) - X; (х40 )т " (л4 -х^); i = 1, 2, 3. (и) Физическим условиям удовлетворяют только такие значения 4-импульса, которые имеют отрицательные значения инвариантного квад рата длины 4-импульса, т. е. Поскольку в рамках нашей модели мира уединенных тел для любого инерциально движущегося тела существует такая система отсчета, в которой это тело покоится (р' = О, Е' = т0с2), между значениями импульса и энергии должно выполняться соотношение, вытекающее из (12): 2 F 2 2 р --^ = -тй с <0. (13) Выражая отсюда энергию Е, мы получаем теоретическое обоснование тому, что в эмпирически установленном законе динамики инерциального движения (8) мы гипотетически (по «подсказке» ньютоновской механики) квадратный корень в знаменателе правой части первого равенства «определили» как энергию тела. Поэтому «выведенное» из (13) соотношение, связывающее импульсную и энергетическую составляющие 4-импульса, вытекающее из физически возможных значений для квадрата длины вектора 4-импульса _ / 24 2 2 ■ НЮ А - Mg С * С Р ’ представляет собой некое «дисперсионное соотношение.» между энергией и импульсом релятивистской классической материальной точки. Ниже мы покажем, что в основу построения динамики тел, находящихся под действием сил, зависящих от положения тела в пространстве, может быть положена инвариантность 4-импульса, в составе которого дисперсионное соотношение модифицируется в соответствии с феноменологическим предположением о зависимости массы покоя тела от состояния «возбуждения» пространства наличием в нем взаимодействующих тел. Тщательный анализ поведения двух взаимодействующих «свободных» (от геометрических и кинематических связей и ограничений) классических материальных точек (известная «задача двух тел» [4]), «вторгающихся» в мир уединениных таких же классических материальных точек (на его основе строится релятивистская теория о существовании и множественности инерциальных систем отсчета, в рамках которых обычным способом производится регистрация поведения новых объектов — свободных взаимодействующих (только между собой!) тел), показывает, что в случае тел с сильно различающимися массами задача фактически сводится к рассмотрению движения одной свободной материальной точки в почти инерциальной системе отсчета, связанной с более массивным телом, пространство вокруг которого находится в возмущенном состоянии, феноменологически описываемом как центральное силовое поле. Теперь свободная материальная точка с так называемой приведенной массой (фактически равной массе менее массивного тела) будет проду- пировать в инерциальной системе отсчета кинематический след не прямолинейного, а если и прямолинейного, то неравномерного характера. Именно с этого момента классическая механика начинает обсуждать постулаты Ньютона («I, II, Ш законы Ньютона»), При нашем подходе необходимость в подобных постулатах появляется в связи с построением экстраполяционной формулы для свободной классической материальной точки в квазиреЛятивистском приближении. Во-первых, мы полагаем («постулируем» как индуктивную гипотезу, полученную на основе обобщения эмпирических данных), что движение свободной материальной точки происходит так, что вблизи каждого момента времени можно выделить интервал (| t+dt), в течение которого тело движется прямолинейно и равномерно в том темпе локально инерциального движения, который имеет тело в момент t; этот темп называется мгновенной скоростью тела u(t). Этот темп обусловливается импульсом и энергией тела, которыми оно обладает «в начальный момент» рассматриваемого интервала времени и, согласно (10) для данного интервала квази-нерциальности, будем иметь: Заметим, что к концу интервала kt,t + dt ) отношение составляющих 4-импульса будет иметь несколько иное значение, равное (<~р / Е) . Поэтому важнейшей задачей теории является выяснение того, каким образом будет изменяться это отношение в действительности. При эмпирическом изучении поведения взаимодействующих тел, теоретически оформляемом в рамках ньютоновского приближения, в частности, в рамках задачи двух тел, выясняется, что полная энергия тела остается неизменной с течением времени. Следовательно, во второй формуле (15) квадратный корень в знаменателе не должен изменять значения, что невозможно, так как импульс при движении тела необходимо изменяется (иначе мы имели бы дело с пря-; молинейным и равномерным движением). Разрешение этого противоречия можно найти на пути обобщения понятия релятивистского 4-импульса для свободной материальной точки, движущейся в специфически возмущенном пространстве, эволюция которого подчиняется строгому закону сохранения энергетической составляющей модифицированного 4-импульса. Поскольку согласно предположению о том, что в каждый момент движения свободной материальной точки существует временной интервал, в течение которого тело движется почти инер-циально со скоростью, равной скорости квази-инерциального движения, продуцируемой импульсом и энергией тела в этом временном интервале, существует локальная инерциальная система отсчета, в которой это тело находится в покое. В следующем, смежном временном интервале инерциальности 4-импульс тела может измениться, но при этом, как подсказывает ньютоновская версия, или, что эквивалентно, эмпирический закон, установленный в области малых значений импульса, энергия должна оставаться неизменной и импульс р не может изменяться. Поэтому для объяснения изменения импульса при неизменности энергии остается одна возможность, а именно — допустить, что силовое возмущение пространства ведет к тому, что масса покоя тела в этом пространстве имеет другую величину, нежели та, которую она имела бы в «пустом» пространстве, причем эта новая масса покоя зависит от интенсивности взаимодействия в тех точках, в которых оно находится в каждый момент движения. При таком предположении условие инвариантности 4-импульса (при переходе из основной ИСО О в ту инерциальную систему отсчета, в которой тело, находясь в течение данного интервала ква-зинерциальности в определенной точке «своего» пространства, которая отвечает точке r(t) основной ИСО О, будет относиться к категории покоящихся уединенных материальных точек), может быть записано в виде; Е2 2 2 Р (О-™ = -(то+Дто(г)) с ; (16) где Дт0(г) представляет собой, разумно предположить, весьма малую добавку к массе покоя т0 в пустом пространстве. Если теперь расчитать изменение 4-импульса, связанное с движением тела из одного интервала квазиинерциальности в смежный интер- вал, то, опираясь на формулу (16), получим: „2 г2 -.2 Е Е (p + dp) -"х--р ^^ = с1 ел _ 2 2 = -(т0 + Дт0(г + dr)) с + _22 + (mQ + Дт0 (г)) с использовано для построения новой функции, по значениям которой можно вычислять значение неизменной во все время движения энергии £ тела. Рассмотрим, какой вид принимает искомая функция в квазирелятивистском приближении. Из (16) находим для Е выражение: / \2 4 2 2 Е - Е - ij\m0 + Дт^г)) с + с р (О = Разлагая в степенной ряд величину ЭДтп(г) Дт0 (г + df) = Д/и0 (г) +--------dr*..., (18) dr [ 4 2 _ 2 42 4 ^Оно с +с р (г)) + 2m0Avn0(r)c + (Д/п0) с = и подставив это в (17), получим, пренебрегая членами второго порядка малости и выше, следующий результат: - . 4 /ШдШПуС 4 2^2 тос + с р (Г) 2pdp = ~2m0 д(Дт0(г)е2) -----г-------dr или 2m Если вновь ввести понятие фазового пространства для свободной материальной точки, то соотношение (19) можно интерпретировать как характерную особенность любого малого участка фазовой траектории и потому, проинтегрировав это вдоль произвольного конечного ее участка и учитывая обычным образом характер подинтегральных выражений, можно получить: где интегрирование осуществляется вдоль соответствующего участка пространственной траектории L Сравнивая (20) с теоремой о кинетической энергии, мы видим, что, во-первых, сила в центральном силовом поле действительно имеет потенциальный характер, во-вторых, в качестве потенциальной энергии выступает характерная для релятивистского подхода величина Щг) = &т0(г)с~ (21) Это согласие релятивистского подхода с феноменологически полученными результатами в ньютоновском приближении придает уверенность в том, что соотношение (16) может быть 2т0Д/и0с 4 2 2 тос + с р (/) 4 W 4~" 2 2 тос *с р (t) ^ПдС *С р (Г) +<7(Г), где t/(r) = Дт0(г)с2 (22) Таким образом, в правой части мы получаем выражение ^то с4 +с2р2(Г) + U(г) = 2 тос _2 Р +-— 2т0 + U(r) = + (f/(r) + m0c2) 2m0 которое в квазирелятивистском приближении может быть представлено в форме: ирел(г) = тос* + U^r) = 2 2 2 (24) = т^с + Дт^с = (mQ + Ат0)с ; Отсюда следует, что, во-первых, эта функция напоминает функцию Гамильтона свободной материальной точки в ньютоновском приближении, во-вторых, фигурирующая здесь полная релятивистская потенциальная энергия, как и следовало ожидать, состоит из двух частей —- из энергии покоя тела в пустом пространстве и дополнителной энергии за счет изменения массы покоя в возмущенном пространстве. Таким образом, при релятивистском подходе потенциальная энергия определяется точно в отличие от ньютоновской механики, где она определяется с точностью до произвольной постоянной. Наконец, убедимся, что если вычислять.значения энергии Е с помощью функции Н ры<?- Р) = Vm0 А-с" р" <0 + ^(г) = Е, (25) то она оказывается характеристической (гамильтоновой) функцией свободной материальной точки, движущейся в центральном силовом поле, определенной в квазирелятивистском приближении. Действительно, поскольку полный дифференциал этой функции на любом малом интервале времени должен равняться нулю, то, дифференцируя левую часть (25), мы получим: dr „ ^Н Р^ ^_ ^Н р^ dt др dt др Наконец, дифференцируя (25) и подставляя полученные выражения в правые части (27), получаем уравнения движения свободной материальной точки в квазирелятивистском приближении в рамках задачи двух тел с сильно отличающимися массами: dr с p(t) ! 2 4 2-2, . ^?н0с + с р (t) dp _ d(Am0(r)) dt dr Окончательно система интегральных уравнений для приведенного тела будет иметь вид: ^('(О,?^ ^ рел dr ^рел dp —£--+ —£-— — dr dt др dt г(0 = д, + j , ■ - . . dt; 0-^m0 с + с р (t) _ Гд(Дт0(г)) PW р0- 1---— 10 дг Как можно показать, условием равенства (26) является равенство вектора фазовой скорости свободной материальной точки нормали к вектору градиента характеристической функции, являющейся к тому же ее интегралом движения: При условии малости отношения Y = Р / rnoc « 1 эти уравнения совпадают с системой интегральных уравнений для свободной материальной точки в ньютоновском приближении [4]. Лостулилс j‘4,j93,.07.