Уравнения пути и скорости посевного агрегата переменной массы в продольно-вертикальной плоскости

Введение. При движении посевного машинно-тракторного агрегата происходит высев семян высевающими аппаратами. В результате масса семян в семенном ящике сеялки (ок) уменьшается [2], а следовательно, уменьшается с течением времени и масса агрегата [3]. Можно привести много примеров, где масса агрегата изменяется в процессе движения. В сельском хозяйстве это, например, посевные, посадочные агрегаты, агрегаты для разбрасывания удобрений и т.д., масса которых изменяется вследствие высева, посадки семенного материала или разброса удобрений.

Цель исследований. Показать оценку кинематических параметров движения посевного машиннотракторного агрегата переменной массы.

Методы и результаты исследований. Посевной машинно-тракторный агрегат (рис., а ), рассматривали как механическую систему, состоящую из четырех тел: трактор, сцепка, конструкция сеялки (без семян) и семена в семенном ящике.

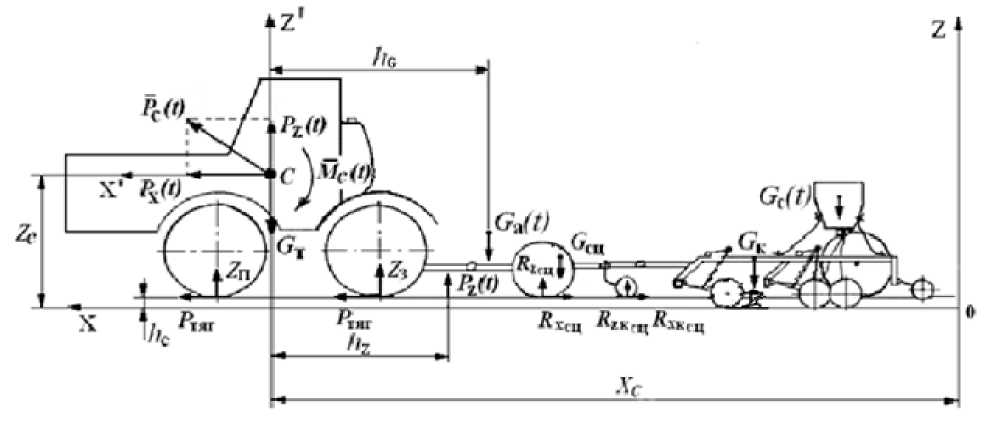
а

Силы, действующие на посевной агрегат в продольно-вертикальной плоскости: а – на трактор и сцепку; б – на сеялку

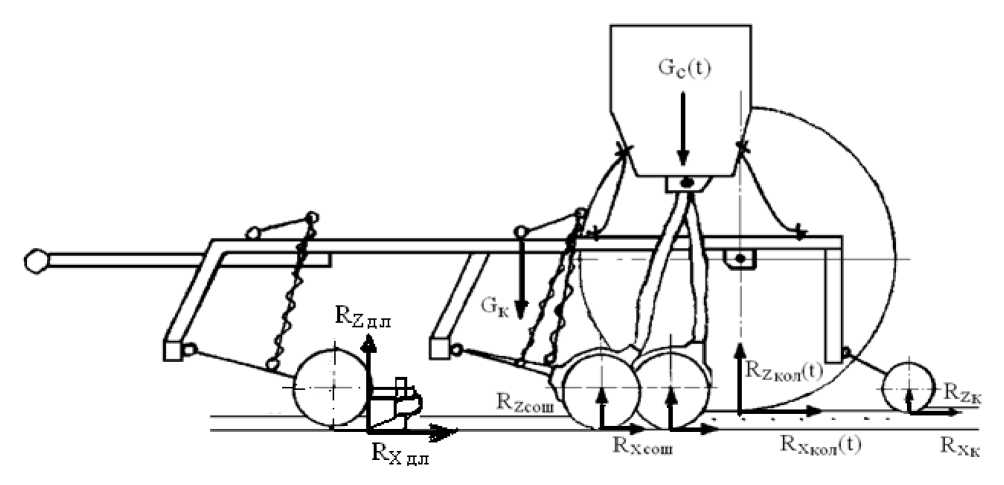
б

Окончание рис.

Чтобы найти уравнения движения механической системы в обобщенных координатах, пользовались уравнениями Лагранжа. Число этих уравнений равно числу степеней свободы системы. Данными уравнениями можно пользоваться для изучения движения любой механической системы независимо от того, сколько тел входит в систему, как движутся эти тела и какое движение рассматривается [7].

Центр масс системы (агрегата) сосредоточили в центре массы трактора (т. С). Данная механическая система имеет три степени свободы и ее положение однозначно определяется координатами Х_с, Z _c центра масс системы (агрегата) и углом (р поворота системы (агрегата) вокруг оси ОУ, перпендикулярной к продольно-вертикальной плоскости и проходящей через центр масс (т. С) [3].

Положение механической системы (агрегата) (рис., а ), однозначно определяется тремя обобщенными координатами [3]:

Q 1 = Х с , Q 2 = Z c , з = ^р -

Дифференциальное уравнение движения посевного агрегата переменной массы в продольновертикальной плоскости (рис.) по обобщенной координате q 1 = Х с имеет вид [3]:

[ (т т + m сц + n m к) + n m с (t) ] Хс - n qm Х.с = Ртяг - г                    r        n d кат пкол I (1 — ё)С 1 р у к ty)fK +

^(G CЦ оп + ^П сц ^G CЦ ус ^)f CЦ ^{— П} |(и к + 9 ^(т о 9 я ^—                 Й

("• ст ⁺ 1)

+ к (^х дл + Rх сош + ^х к) + Рпр ] , где тт , тсц , тк , тс (t) - массы трактора, сцепки, конструкции сеялки (без семян) и семян соответственно, кг; n - количество сеялок в агрегате, шт.; q.cc - секундный высев семян, кг/с; Х.c, Х.с - скорость и ускорение центра масс системы соответственно, м/с, м/с2; Ртяг - сила тяги колес трактора, Н; Gcц оп, Gсц ус -сила тяжести сцепки, приходящаяся на опорные и самоустанавливающиеся колеса, Н; псц - количество са-моустанавливающихся колес сцепки, шт.; fcц, Ж - коэффициент сопротивления перекатыванию колес сцепки и сеялки, соответственно; Gк - сила тяжести конструкции сеялки (без семян), Н; 9 - ускорение свободного падения, м/с2; то - масса семян в семенном ящике сеялки в начальный момент времени (при полностью заполненном ящике), кг; qя - коэффициент использования вместимости емкости; dкат - диаметр катушки высевающего аппарата, м; пкол - частота оборотов опорно-приводного колеса сеялки, с-1; i - передаточное отношение от опорно-приводного колеса сеялки к валу высевающих аппаратов; г - коэффициент скольже- ния колес сеялки; ℓр – длина рабочей части катушки, м; C – толщина активного слоя, м; γ – объемный вес семян, кг/м3; k – количество комплектов рабочих органов у одной сеялки (высевающих аппаратов, дисколаповых рабочих органов, сошников, прикатывающих катков) [6], шт.; пст - показатель степени, определяемый опытным путем (для пшеницы nст = 2,6 [4]); t – время, с; Rx дл – тяговое сопротивление рабочих органов (дисколаповых) для разрушения почвенной корки, Н; Rx сош – тяговое сопротивление сошников, Н; Rx к – тяговое сопротивление прикатывающих катков, Н; Рпр – прочие сопротивления сеялки, Н.

Правая часть дифференциального уравнения (1) равна Р х ( t ):

-

Р х (t)  Р тяг    (^ сц оп + ^п сц G сц ус ^{) f}cn    ^п [(^ к + 9 ^(т о 9 я ^-

^ dкат Пкол I (1 £)С 1 р у к      + к (R + R + R + р к XX ДЛ X сОШ X к пр

^(П ст ^{+ 1)}

где Р х (t) – главный вектор в проекции на ось ОХ (рис., а ), Н . Поэтому перепишем

[ (т т + m сц + n m_K) + n m с (t) ] Х. ,с - n q cc Х , c = Р х (t) .                           (3)

Это дифференциальное неоднородное уравнение с непостоянными коэффициентами (уравнение Эйлера [1, 5]).

Чтобы решить данное уравнение, необходимо произвести замену переменной.

Для области n m с (t) + (m т + m сц + n m к ) > 0

или после преобразования с учетом выражения т с (t) = m o П я - q cc t [2]

- n qcc t + М > 0, где М = n m о у я + m m +m сц +n m к - постоянная часть массы агрегата, кг;

^ dKam Пкоп i (1~^) 1рС у к                -                    / qcc =--------------р----- - секундный высев семян, кг/с.

Введем независ^переменную и , полагая:

	α t + b = e u , где а = - n q cc , b = М, (4) u-h t = — .                               (5) а
Откуда	u = ℓ n (α t + b) .
Тогда	= Х = а е — d^ , d 2 x = Х = а2е~ 2 (-   ) .             (6) dt                du     dt 2                  vdu 2 du                 ' '

После подстановки выражений (4) и (6) в уравнение (3) оно преобразуется в неоднородное уравнение с постоянными коэффициентами и примет вид:

Х = а Р х (t) е ^и .                                            (7)

Общее решение однородного дифференциального уравнения

Х = о будет                    Х0 = С1 + С2 u.

Общее решение неоднородного уравнения (7) можно записать в виде суммы

Х = Х 0 + Х* ,                                        (8)

где Х - частное решение неоднородного уравнения (7).

Для нахождения частного решения уравнения (7) преобразуем его правую часть с учетом того, что мы произвели замену переменной t на u .

На основании выражения (2)

Рх (t) = n g q^ fK t + Р , где Р = Ртяг - Rрсц - n Gк f - n g fK mo Пя - n k Rрро - n Рпр - постоянная (неизменяющаяся) часть главного вектора в проекции на ось ОХ, Н; Rхсц - горизонтальная равнодействующая сил сопротивления сцепки, Н; R х ро — горизонтальная равнодействующая сил сопротивления рабочих органов сеялки, Н.

Rрсц = ^Н Rх сц + псцRх ксц , Rр ро = nk (RX дл + Rx сош + Rxk) , где Rх сц - горизонтальная реакция на опорном колесе сцепки, Н; m - количество колес сцепки, шт.; Rхксц -горизонтальная реакция на самоустанавливающихся колесах сцепки, Н.

Тогда с учетом выражений (4) и (5) после некоторых преобразований, получим :

4 Р х (t) е^и = ^{9 / к} ₂ ^М + Р е^и - () е^2и                       (9)

а ²                  п ² Q c_C             ~п² q c_c

Правая часть уравнения (9) есть сумма двух функций f i (t) и f . 2 (t) . Тогда частное решение можно представить в виде суммы

Х* = Х .1 + Х* 2, где Х.1 и Х.2 есть соответственно решения уравнений

Х = -

( ^{9 / к} ) р^И п ² q Cc        ^,

у _ 9 /к М + Р   ,J л = —-—— е и п2 qCc т. е.

и уравнение (8) примет вид:

9 / к М + ^Р  _ы

& п ² q Cc

,

Х * ₂ = -

( ^{9 / к} ) _р 2и п ² q Cc        ,

Х = Хо + Х .1 + Х 2 , а общее решение уравнения (7) будет:

Х = C i + С 2 1 n (- n q^ t + М) + [ ^{4(9 / к М} ₄ + 2 Р2 ^}  ° ^{Ок М} ]( - n ....... t + М).                  (10)

При начальных условиях:

t = 0 ; Х = 0 ; X. = 0 .

Произвольные постоянные C i и С 2 будут равны:

С 1 =

О 0_к М 2 + 2 Р М

2 О² 0 2

t n (М) -

4 М ( 0 о_к М + Р )- 0 о_к М²

4 О² 0 2

С 2

О 0_к М 2 + 2 Р М

2 О² 0 20

.

Подставив (11) и (12) в (10), окончательно получим

2 М ( 0 О к М + 2 Р ) 10 (- М -)- [ 4 ( 0 О к М + Р )- 0 О к ( М + М а ( 0 ))] 0 0_ш О Мд ⁽ о )/

=                                           4 О2 02                                          ’ где Ма (t) = n ( mо 0я — 000 0) + (mm + mсц + n mк) - масса механической системы (агрегата), изменяющаяся с течением времени, кг.

Скорость посевного агрегата (V а ) есть первая производная от пути по времени. Продифференцировав выражение (13), будем иметь:

V а = Х =

М ( о к М + 2 Р ) - [ 2 ( о о к М + Р ) - о к М_а ( о )] М_а ( о ) 2 о о оо М а ( о )

Во время работы посевного агрегата в конце пути должен оставаться запас семян в ящике не менее 10–15 % [8] его емкости. Поэтому оо тоф = 1,101,15 ’ где тоф - фактически высеваемая масса семян из семенного ящика, кг.

Время о , за которое будет высеяна фактическая масса семян, равно [2]:

о о о_я

( 1 , 1 . 1 , 15 ) о оо

Тогда длина пути L = V a ∙ t , на котором будет высеяна фактическая масса семян, с учетом выражений (14) и (15) будет равна:

L = М ( о о_к М + 2 Р ) - [ 2 ( о о_к М + Р ) - о о_к М а ( о )] М а ( о ) _х т ₀ Ч я

2 о о 2 М а ( о )                             (1,1.1,15) .

Выводы

Получены уравнения пути (13) и скорости (14) посевного агрегата переменной массы, которые зависят от постоянной (неизменяющейся) части главного вектора (Р) в проекции на ось ОХ, постоянной (М) и изменяющейся частей (М а (t)) массы агрегата и секундного высева семян, который в свою очередь зависит от основных конструктивных параметров высевающего аппарата - d кат , 1_р , C.

Полученные выражения могут использоваться при определении длины пути ( L ) для высева фактической массы семян, в конце которого необходимо заправить сеялку (ки) семенами (подвести семена).