Уравнения состояния графовой модели трехмерных упругих тел в декартовой системе координат
Автор: Тырымов А.А.
Статья в выпуске: 3, 2017 года.
Бесплатный доступ
Рассматривается численный метод расчета полей деформаций и напряжений трехмерных упругих тел, дискретной моделью которых служит ориентированный граф как идеализация гипотетических приборов, необходимых для измерения деформированного состояния тела. В соответствии с предлагаемым методом упругая среда разделяется на отдельные элементы плоскостями, параллельными координатным. Для каждого элемента, полученного при декомпозиции, строим элементарную ячейку (подграф), являющуюся его моделью. Она представляет собой комплект измерителей, установленных на элемент для определения его деформированного состояния. Уравнение элементарной ячейки получаем, пользуясь инвариантом, сохраняющимся при преобразовании элемента в ячейку. В качестве инварианта используем энергию деформации. Граф тела конструируем с помощью операции объединения элементарных ячеек. Он отражает характер декомпозиции и является дискретной моделью анализируемого сплошного тела. Структурные свойства графа задаются рядом специальных матриц, наиболее важными из которых являются матрицы инцидентности, контуров, хорд, путей. Уравнения состояния исходного тела получаем с помощью преобразования обобщенных координат элементов тела, полученного в результате декомпозиции, к системе координат, описывающих тело в целом. Преобразования осуществляются несингулярными взаимно обратными матрицами. Специфическая особенность графов, используемых в качестве дискретных моделей сплошного тела, заключается в том, что они позволяют конструировать несингулярные матрицы и исключить их обращение. Квадратные взаимно обратные матрицы преобразования созданы путем сочленения прямоугольных матриц, представляющих собой разнообразные элементы графа. Вывод определяющей системы уравнений основан на использовании вершинного и контурного законов Кирхгофа для графов, а также свойств построенных квадратных матриц преобразования. Возможности графового метода проиллюстрированы решением тестового примера.
Математическое моделирование, теория упругости, ориентированный граф, напряжения, деформация, матрица инцидентности, матрица контуров
Короткий адрес: https://sciup.org/146211689
IDR: 146211689 | УДК: 539.3 | DOI: 10.15593/perm.mech/2017.3.11
Текст научной статьи Уравнения состояния графовой модели трехмерных упругих тел в декартовой системе координат
PNRPU MECHANICS BULLETIN
Графы широко используются как структурные модели физических и технических систем, допускающих идеализированное представление в виде схем с сосредоточенными параметрами [1–6]. Сюда относятся электрические цепи, механизмы, стержневые конструкции, теплообменники, акустические системы, разнообразные комбинированные системы, такие как электромеханические, гидромеханические, механоакустические и др. Объясняется это рядом достоинств графовых моделей. Одно из обстоятельств, способствующих применению графов для описания различных технических систем, заключается в их связи с операциями измерения основных переменных, однозначно определяющих состояние этих систем. Физическая природа переменных изменяется от одного класса систем к другому, в то время как техническая суть операции по их измерению остается неизменной. Подобный подход позволяет представить систему ее переменными, изображенными в виде графа, а граф использовать при анализе этой системы.
Однако помимо преимуществ, связанных с наглядностью представления структуры и связи основных переменных, графы позволяют целенаправленно в рамках определенного алгоритма провести сложные математические преобразования. Анализ физических и технических систем сводится к получению уравнений состояния системы на основании уравнений состояния ее частей. Теория графов позволяет разработать систематическую методику вывода этих уравнений. Объединение описаний частей в описание связной системы осуществляется с помощью матриц, характеризующих структуру графа.
Анализ системы с сосредоточенными параметрами с использованием матричных методов возможен на основе сетевой модели Г. Крона. Подход Крона [7, 8] основан на объединении структурных свойств электрической цепи, представляемых схемой соединения ее компонентов, с функциональными свойствами, представленными уравнениями состояния компонентов. Применяя аналоговое моделирование, Крон предложил использовать электрические цепи для представления самых разнообразных физических, технических и экономических систем. Были разработаны эквивалентные электрические сети, предназначенные для моделирования задач гидродинамики, электрического поля, квантовой механики, линейного программирования [7–10].
При построении электрической сети, эквивалентной упругому телу, Крон принял, что механические напряжения моделируются электрическими токами, а деформации – разностями потенциалов. Однако необходимость учета характеристик реально существующих электрических компонентов и процессов привело к тому, что элементарные ячейки Крона отличаются сложностью конфигурации. Так, в элементарную ячейку для непосредственного физического моделирования плоского напряженного состояния упругого тела входит 12 компонентов со сложным их соединением [11]. Обращая основное внимание в своих работах на универсальность возможностей использования в качестве моделей эквивалентных электрических сетей в различных областях науки и техники, Крон не приводит методик по их конструированию и разработке алгоритмов при определении параметров элементарных ячеек.
Подход Крона не получил распространения применительно к задачам механики сплошной среды. Опираясь на идеи Крона, Е.Г. Кузовков [12–14] предложил использовать электрические ячейки только для отображения связей и характеристик моделируемой упругой среды. Это позволило в компонентах ячеек не учитывать такие свойства реально существующих электрических элементов, как потери, утечки, взаимные наводки. Подобный подход дал возможность при описании упругого элемента применить ячейку, состоящую всего из четырех компонентов. Параметры ячейки определялись сравнением выражений, полученных на основе законов Ома и Гука. В работе [15] Е.Г. Кузовков обратил внимание на то, что при моделировании напряженно-деформированного состояния упругих тел можно обойтись без электромеханической аналогии, если эквивалентную электрическую сеть трактовать как ориентированный граф.
Способ конструирования графовой модели, ее конфигурация, применение специальным образом сконструированных матриц для вывода определяющей системы уравнений применительно к плоской и осесимметричной задачам теории упругости предложены Е.Г.Кузовковым и подробно изложены в [15–20]. В работе [21] на основе графовой модели построен двумерный сингулярный элемент для расчета напряженно-деформированного состояния в окрестности особых точек разреза. Использованию графового метода для анизотропных и неоднородных сред посвящены работы [22, 23]. Графовая модель упругой среды в полярной системе координат рассматривалась в [24].
В работе [25] в качестве дискретной модели трехмерного упругого тела в декартовой системе координат используется ориентированный граф как идеализация гипотетических приборов, необходимых для измерения деформированного состояния тела. В этой работе приведено описание элементарной ячейки – подграфа, соответствующего одному элементу, полученному при разбиении исходной области на мелкие части.
При определении конфигурации элементарной ячейки, так же как предложено в [25], «область, занятую телом, покрываем сетью координатных плоскостей x = const, y = const, z = const, между узлами которых устанавливаем гипотетические измерители, определяю- щие абсолютные нормальные деформации 5xx, 5yy, 5zz и деформации 5yx, 5xy, 5zx, 5xz, 5zy, 5y, обусловленные сдвигом. Полученную сеть измерителей преобразовываем в граф, представляя каждый из приборов дугой, а узлы, между которыми осуществлялось измерение, – вершинами графа. При этом вместо собственно измерителя будем ставить символ, отражающий природу измеряемой величины. В результате получаем элементарную ячейку прямоугольного шестигранного элемента, имеющую 36 дуг и 24 вершины и состоящую из трех компонент (рис. 1):
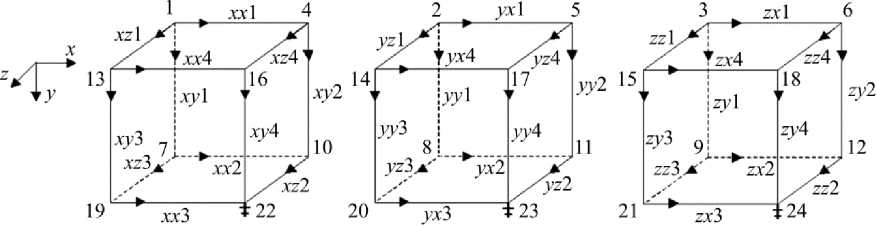
Рис. 1. Элементарная ячейка, состоящая из трех компонент Fig. 1 An elementary cell consisting of three components
Вершины с номерами 22, 23, 24 – корни подграфов соответствующих компонент элементарной ячейки. Каждая из дуг графа отображает одну из следующих пар параллельных и последовательных переменных:
( 5 xx , f x ), ( 5 yy , f y ), ( 5 zz , f zz ), ( 5 yx , fyX ), ( 5 xy , f xy ),
( 5zx , fx ), ( 5xz , fz ), ( 5zy , fy ), ( 5yz , fyz ), где fxx, fyy, fzz и fyx, fxy, fzx, fxz, fzy, fyz – нормальные и тангенциальные внутренние силы (обобщенные напряжения). Таким образом, дугам элементарной ячейки соответствует следующая пара векторов:
t xx 1 xx 4 yy 1 yy 4 yz 1 yz 4
{ f } c = { f ,...,, f ,f ,...,f ,...,f ,...,f / } ,
{ 8 } C = { 5 xx 1 ,-, 5 xx 4 , 5 yy 1 ,-, 5 yy 4 ,..., 5 yz 1 ,-, 5 yz 4 } .
где символ t обозначает операцию транспонирования, а индекс с указывает на принадлежность переменных отдельной элементарной ячейке.
Использование в качестве инварианта перехода к модели энергию деформации элемента среды позволило в [25] получить матрицу жесткости для восьмиузлового шестигранного прямоугольного упругого элемента с 24 степенями свободы при линейной аппроксимации деформаций.
В данной работе рассматривается метод построения определяющей системы, описывающей связное пространственное тело. Он основан на объединении описаний отдельных элементов, полученных в [25], в описание связного тела, которое осуществляется с помощью матриц, характеризующих структуру графа. Решение полученной системы позволяет определить напряженно-деформированное состояние упругого тела.
1. Матричное представление структурных элементов графа
В анализе напряженно-деформированного состояния упругого тела на основе графовой модели используются разнообразные структурные элементы. Поскольку терминология теории графов до конца не стандартизирована, дадим определения основных используемых ниже понятий [5, 26-28].
Маршрут - конечная последовательность необязательно различных дуг, у которых одна из вершин первой дуги является вершиной второй, оставшаяся вершина второй -вершиной третьей и т.д. Путь - незамкнутый ориентированный маршрут, не содержащий повторяющихся дуг. Граф называется связным, если в нем существует путь между каждой парой вершин. Контур графа - замкнутый ориентированный маршрут, не содержащий повторяющихся дуг. Дерево - связанный подграф, не содержащий контуров. Остов-ное дерево - дерево, содержащее все вершины исходного графа. Дуги дерева называются ветвями. Хорды - дуги графа, не принадлежащие дереву. Компонента графа - максимально связный подграф этого графа. Если исходный граф состоит из нескольких компонент, то деревья компонент образуют лес. Вершина является корнем дерева, если из нее существует ориентированный путь по всем остальным вершинам этого дерева. Базисный контур - контур, образованный хордой и теми ветвями дерева, которые составляют единственный путь между ее концевыми вершинами.
Число линейно независимых базисных контуров равно числу хорд графа и определяется формулой ц ( G ) = m - n + к , где ц ( G ) - цикломатическое число; m - число дуг; n -число вершин; к - число компонент графа.
При изучении структурных связей, порождаемых графом, удобно использовать матричный аппарат.
Рассмотрим матрицы, задающие отношения инцидентности между дугами, с одной стороны, и вершинами, путями, хордами и контурами - с другой [5,6]. Расположение строк и столбцов в этих матрицах определяется номером вершин и обозначением дуг графа.
Матрица инцидентности . Матрица инцидентности [ A ] ориентированного графа, имеющего n вершин и m дуг, является матрицей размером n х m с элементами a ij ( i = 1, 2, .., n ; j = 1, 2, .., m ), определяемыми следующим образом:
1, если j -я дуга инцидентна i вершине и выходит из нее,
a
ij
< 0, если j -я дуга не инцидентна i вершине,
- 1, если j -я дуга инцидентна i вершине и входит в нее.
Ранг матрицы [ A ] равен n - к , где к - число компонент графа и совпадает с рангом графа rk. Строки матрицы инцидентности соответствуют вершинам, которые остаются изолированными при удалении дуг, перечисленных в соответствующих строках. Если оставить невырезанными корневые вершины, то получим усеченную матрицу инцидентности. Строки в этой матрице перечислены в порядке возрастания номеров вершин от 1 до 21, столбцы соответствуют дугам графа в порядке xx 1, yy 1, zz 1, xx 2, yy 2, zz 2, xx 3, yy 3, zz 3, xx 4, yy 4, zz 4, xy 1, yx 1, xz 1, zx 1, yz 1, zy 1, xy 2, yx 2, xz 2, zx 2, yz 2, zy 2, xy 3, yx 3, xz 3, zx 3, yz 3, zy 3, xy 4, yx 4, xz 4, zx 4, yz 4, zy 4 .
Матрица корневых путей . Матрицей корневых путей остовного дерева [ P ] ориентированного графа называется матрица, элементы которой p ij определяются по следующему правилу:
1, если j-я ветвь входит в i путь и ее направление не совпадает с положительным направлением пути,
Р у =
0, если j -я ветвь входит в i путь,
-1, если j-я ветвь входит в i путь и ее направление противоположно направлению пути.
Матрица путей строится в соответствии с рис. 2, где изображены деревья элементарной ячейки.
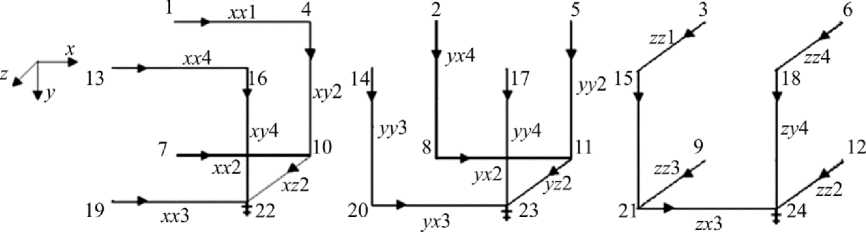
Рис. 2. Деревья элементарной ячейки
Fig. 2.The trees of the elementary cell from
Матрица путей имеет размер rk х m . Строки матрицы путей соответствуют вершинам, из которых начинается путь к корню, столбцы – дугам, образующим путь. За положительное направление пути принимаем направление от вершины к корню. Каждый путь обозначаем индексом вершины, которую данный путь связывает с корнем. Нумерация строк и столбцов точно такая, как и в матрице инцидентности.
Матрица хорд . Матрицей хорд [ B ] называется матрица с элементами b ij , где
1, если j -я дуга является хордой, входящей
Ь..
ij
= <
0,
в i базисный контур, если j-я дуга является ветвью или хордой,
не входящей в i базисный контур.
Матрица хорд имеет ранг, равный цикломатическому числу p ( G ) = m - n + k , ее размер - ц ( G ) х m . В матрице хорд индексация строк и столбцов такая же, как у матрицы базисных контуров. Элементы матрицы [B], стоящей на пересечении строк и столбцов с нумерацией xy 1, yx 1, xz 1, zx 1, yz 1, zy 1, zx 2, zy 2, xy 3, xz 3, yz 3, yx 4, xz 4, zx 4, yz 4, равны единице, а остальные равны нулю.
Матрица базисных контуров . Матрицей базисных контуров [ C ] ориентированного графа называется матрица, элементы c ij которой определяются так:
1, если j-я дуга входит в i базисный контур и совпадает с его направлением, cj = < 0, если j-я дуга не входит в i базисный контур,
-1, если j-я дуга входит в i базисный контур и противоположна по направлению.
Каждый базисный контур содержит только одну хорду и те ветви дерева, которые кратчайшим путем связывают ее вершины. Направление базисного контура задается направлением определяющей хорды. Ранг матрицы базисных контуров определяется линейно независимыми контурами, их число ц ( G ) = m - n + k , т.е. совпадает с цикломатиче-ским числом графа. Размер матрицы контуров [ C ] равен p ( G ) х m . Контуры матрицы [ C ] упорядочены согласно выбору задающих их хорд. Порядок расположения строк соответствует хордам xy 1, yx 1, xz 1, zx 1, yz 1, zy 1, zx 2, zy 2, xy 3, xz 3, yz 3, yx 4, xz 4, zx 4, yz 4], столбцы – дугам графа с прежней индексацией.
В трехмерной декартовой системе координат транспонированная матрица [ C ] t выглядит так:
|
xy 1 yx 1 |
xz 1 zx 1 |
yz 1 zy 1 zx 2 |
zy 2 xy 3 xz 3 yz 3 yx 4 xz 4 zx 4 yz 4 |
|
|
xx 1 |
–1 |
–1 |
||
|
yy 1 |
–1 |
–1 |
||
|
zz 1 |
–1 |
–1 |
||
|
xx 2 |
1 |
–1 |
||
|
yy 2 |
1 |
–1 |
||
|
zz 2 |
1 |
1 |
||
|
xx 3 |
1 1 |
|||
|
yy 3 |
1 |
–1 |
||
|
zz 3 |
1 –1 |
|||
|
xx 4 |
1 |
–1 |
||
|
yy 4 |
1 1 |
|||
|
zz 4 |
1 |
–1 |
||
|
xy 1 |
1 |
|||
|
yx 1 |
1 |
|||
|
xz 1 |
1 |
|||
|
zx 1 |
1 |
|||
|
yz 1 |
1 |
|||
|
[C] t = zy 1 |
1 |
|||
|
xy 2 |
–1 |
–1 |
–1 |
|
|
yx 2 |
–1 |
–1 |
–1 |
|
|
xz 2 |
–1 |
–1 –1 |
||
|
zx 2 |
1 |
|||
|
yz 2 |
–1 |
–1 –1 |
||
|
zy 2 |
1 |
|||
|
xy 3 |
1 |
|||
|
yx 3 |
1 |
1 –1 |
||
|
xz 3 |
1 |
|||
|
zx 3 |
–1 |
–1 |
–1 |
|
|
yz 3 |
1 |
|||
|
zy 3 |
–1 |
–1 |
–1 |
|
|
xy 4 |
1 |
–1 1 |
||
|
yx 4 |
1 |
|||
|
xz 4 |
1 |
|||
|
zx 4 |
1 |
|||
|
yz 4 |
1 |
|||
|
zy 4 |
1 |
–1 1 |
В матрице базисных контуров и ниже – в матрице линейных комбинаций базисных контуров – записаны только ненулевые элементы.
Заметим, что в третьем, четвертом и пятом столбцах матрицы [C]t число отличных от нуля элементов больше четырех. С увеличением числа элементов, на которые рассечено тело, растет количество дуг графа, и появляются столбцы, содержащие большее число единиц (с тем или иным знаком). Это усложняет процесс программирования и, кроме того, ухудшает точность вычислений. В то же время число отличных от нуля элементов в столбцах матрицы [C]t можно сделать равным четырем при любой степени декомпозиции. Базисные контуры, которые содержат только одну хорду и три ветви, остаются без изменения. В остальных случаях следует перейти от базисных контуров к их линейным комбинациям.
Например, из рис. 2, видно, что в базисный контур C xz 1 входят дуги xz 1, xx 4, xy 4, – xz 2, – xy 2, – xx 1, а в контур C xz 4 – дуги xz 4, xy 4, – xz 2, – xy 2.
Разность этих базисных контуров даст контур C xz 1 , который включает в себя дуги xz 1, xx 4, – xz 4, – xx 1. Таким образом, контуры, полученные линейной комбинацией базисных, содержат две хорды и две ветви. Одна хорда имеет положительное направление и принимается в качестве определяющей данный контур, вторая хорда входит в контур с отрицательным знаком. В результате получим транспонированную матрицу |^ C J линейных комбинаций базисных контуров:
yz1 zy1 zx2 zy2 xy3 xz3 yz3 yx4 xz4 zx4 yz4
xy1 yx1
xz1
zx1
|
xx 1 |
–1 –1 |
||||||
|
yy 1 |
–1 |
–1 |
|||||
|
zz 1 |
–1 –1 |
||||||
|
xx 2 |
1 |
–1 |
|||||
|
yy 2 |
1 |
||||||
|
zz 2 |
1 |
1 |
|||||
|
xx 3 |
1 |
1 |
|||||
|
yy 3 |
1 |
||||||
|
zz 3 |
1 |
–1 |
|||||
|
xx 4 |
1 |
–1 |
|||||
|
yy 4 |
|||||||
|
zz 4 |
1 |
–1 |
|||||
|
xy 1 |
1 |
||||||
|
yx 1 |
1 |
||||||
|
xz 1 |
1 |
||||||
|
zx 1 |
1 |
||||||
|
t yz 1 |
1 |
||||||
|
C 1 = zy 1 |
1 |
||||||
|
xy 2 |
–1 |
||||||
|
yx 2 |
–1 |
–1 |
|||||
|
xz 2 |
–1 |
||||||
|
zx 2 |
1 |
||||||
|
yz 2 |
–1 |
||||||
|
zy 2 |
1 |
||||||
|
xy 3 |
1 |
||||||
|
yx 3 |
1 |
||||||
|
xz 3 |
1 |
||||||
|
zx 3 |
–1 |
||||||
|
yz 3 |
–1 |
1 |
|||||
|
zy 3 |
–1 |
||||||
|
xy 4 |
–1 |
||||||
|
yx 4 |
|||||||
|
xz 4 |
–1 |
||||||
|
zx 4 |
–1 |
||||||
|
yz 4 |
|||||||
|
zy 4 |
–1 |
–1
–1
–1
–1
–1
–1
–1
–1
Структурные матрицы в [20, 23].
для элементарной ячейки в двумерном случае представлены
2. Свойства топологических матриц. Построение несингулярных матриц преобразования
Между топологическими матрицами существуют взаимные связи, выражающие свойства ортогональности или позволяющие по одной из них определить другую [6].
Известно, что матрицы инцидентности и контуров обладают свойством ортогональности:
[ A ][ C ] t = 0, [ C ][ A ] t = 0. (2)
Кроме того, из определения матрицы корневых путей остовного дерева и матрицы хорд следует
[ B ][ P ] t = 0, [ P ][ B ] t = 0. (3)
Действительно, в столбцах матрицы [P], соответствующих хордам, стоят нули, а единицы расположены в столбцах, соответствующих ветвям, в то время как в матрице [B] t в строках, соответствующих хордам, стоят единицы, а ветвям - нули.
С другой стороны, произведение матриц инцидентности и путей основного дерева, а также хорд и контуров дает единичную матрицу:
[ A ][ P ] t = [ I ], [ P ][ A ] t = [ I ]. (4)
[ B ][ C ] t = [ I ], [ C ][ B ] t = [ I ]. (5)
Ранг каждой из матриц [A] и [P] равен рангу графа rk , а ранг матриц [B] и [C] равен цикломатическому числу ц . Это позволяет сконструировать квадратные матрицы размером m х m , так как rk + ц = m , а число столбцов у матриц [A], [B], [C], [P] равно m . Для этого следует применить операцию сочленения двух матриц по вертикали [28], которая заключается в простом приписывании второй матрицы к первой снизу. Таким образом, сначала располагаются все строки первой матрицы, а затем второй - без нарушения их порядка в исходных матрицах. В результате можно построить две квадратные матрицы
A
[ A B ] = „ • [ P C ] =
B
Матрицу [ A B ] можно назвать матрицей дополнений, так как она построена с помощью матрицы инцидентности [ A ], содержащей разрезы, дуги которых дополняют множество изолированных вершин до исходного графа, а матрица [ B ] включает в себя хорды, дополняющие ветви остовного дерева до исходного графа.
Матрицу [ PC ] назовем матрицей маршрутов, поскольку она составлена из матрицы корневых путей [ P ] и матрицы контуров [ C ], т.е. с использованием матриц открытых и замкнутых маршрутов.
Из правил оперирования с блочными матрицами вытекают соотношения
[ A B ] t = [ A t , B t ], [ P c ] t = [ P t , C t ].
Учитывая свойства (2)-(5), получаем
[ A B ][ P c ] t =
A
B
[ P t , C t ] =
AP t AC t
BP t BC
I
I
= [ 1 ] .
Отсюда следует, что матрицы [ Ав ] и [ P C ] ' взаимно обратные, т.е.
[ P c ] t = [ А в ] -1 , [ A b ] t = [P c ] -1 . (6)
Заметим, что строки и столбцы матриц [ Ав ] и [ P C ] имеют одинаковые обозначения. Поскольку связь (6) между этими матрицами получена не с помощью математического обращения, а путем искусственного построения, то при выполнении операции сочленения необходимо специально следить за соответствием распределения строк и столбцов в каждой из матриц, обеспечивая одинаковый порядок.
-
3. Уравнения графовой модели тела
Тело, представленное в виде отдельных элементов, и соответствующая ему совокупность элементарных ячеек описывается уравнением
{ f } = [ К ] { 8 } . (7)
Здесь { f } и { 5 } - векторы внутренних сил и деформаций.
{f}‘={с,«2..-,f.}, {6}'={б.,»2.,-,»l}, причем {f},., {б}, определяются (1), [К] - глобальная несвязная матрица жесткости тела, представленного в дискретном виде:
[К] = diag[Ki., К^.-.К.], где n - число ячеек, образующих граф, а [К]ic определяется формулой (29) из работы [25].
Уравнение (7) связывает внутренние силы с деформациями элементов и не позволяет в общем случае определить напряженно-деформированное состояние тела, поскольку, как правило, заданными бывают внешние силы и перемещения.
Для получения уравнений связного тела, следуя [18], используем преобразования обобщенных координат, описывающих разрезанное на элементы и связное тело. Вводим преобразования переменных с помощью квадратных матриц [ A B ] и [ P C ]:
{F} = [ Ав ]{f} = [ в J{f} = ( Bf ].(8)
{д}=[ Pc ]{6}=|с J{a}=^ С6 ].(9)
Поскольку матрицы дополнений и маршрутов несингулярны, то с учетом (6) возможны обратные преобразования, которые не требуют процедур численного обращения:
{ f } = [ Ав F { F } = [ P C ] ' { F } .
{6} = [Pc]-1 {Д} = [Ав]' {д}.(10)
Подставив в правую часть (7) значения { 6 } из (10), а также умножив это уравнение слева на [ А в ], получаем уравнение, описывающие связное тело:
{F} = [Ав][К][Ав]' {Д},(11)
где
[ Ab ][K ][ Ab ] t =
AB
[ K ] [ A t , B t ] =
AKAt AKB tBKAt BKBt
Следует отметить, что уравнение (11),описывающее напряженно-деформированное состояние дискретной модели, несет информацию о структуре графа и физическом законе Гука. Дифференциальные уравнения равновесия и совместности деформаций при выводе (11) не использовались. В то же время для построенной графовой модели, как показано в [25], уравнения равновесия и совместности деформаций обеспечиваются автоматически как следствие вершинного и контурного законов Кирхгофа [6, 27], которые имеют фундаментальный характер.
Рассмотрим общесистемный вектор сил (8). Его член [ A ]{ f } на основании вершинного закона [5,15] представляет собой вектор вершинных переменных { F } e , которые интерпретируются как заданные внешние силы. Член [ B ]{ f } выделяет часть дуг графа { f } b , являющихся хордами, которые интерпретируются как неизвестные внутренние силы.
Вектор общесистемных перемещений (9) включает в себя член [ P ]{ 6 }, который представляет собой перемещения узловых точек в глобальной системе координат { U }. На основании контурного закона [6,18] член [ C ]{ 6 } равен нулю.
В результате уравнение (11) принимает вид
' Fe ^
< fb V
AKA t AKB t V U ^
BKAt BKBt j( 0 V откуда следует
{F} e =[ A][K ][ A] ‘ {U}=[Ks ]{U}.
Решение последнего уравнения получаем в виде
{ U } = [ K s ] —1 { F } e .
По известным перемещениям определяем деформации, а затем с помощью закона Гука находим напряжения, действующие в каждом элементе.
4. Численные результаты
В качестве примера, иллюстрирующего предлагаемый метод, приведем задачу из [29]. В ней рассматривается расчет напряженного состояния для пространственной структуры, изображенной на рис. 3. Как указано в [29], эта расчетная схема может быть использована для моделирования шахтной выработки для поддерживания кровли при проведении горных работ.
На рис. 3 показана расчетная схема и дискретизация структуры на шестигранные прямоугольные элементы. Изображена восьмая часть расчетной области. Плоскости xy, yz и zx являются плоскостями симметрии. Нормальные перемещения узлов, лежащих в плоскостях симметрии, задавались равными нулю. К нижней поверхности приложена равномерно распределенная нагрузка p = 0,1 МПа, на верхней поверхности исключены вертикальные перемещения. Другие грани конструкции свободны от нагрузки. Размеры, как и в [29], верхнего параллелепипеда 20×20×40 (см), нижнего – 60×60×80 (см). В [29] приведены решения рассматриваемой задачи методом граничных элементов (МГЭ), методом конечных элементов с использованием модифицированных гексаэдров Айронса-Зенкевича, а в работе [30] с помощью шестигранного прямоугольного конечного элемента с применением линейных базисных функций для аппроксимации напряжений. Анализируется концентрация напряжений
σ у / р , вдоль диагонали плоскости соединения кровли и крепи. В расчетах число граничных сегментов в зависимости от версии программ МГЭ составляло 16 либо 44, в МКЭ сетка разбиения на элементы редкая с использованием 274 степеней свободы для ее узлов [29]. Авторы отмечают, что дискретизация слишком грубая и требует более детального описания. Анализ напряжений методом КЭ в [30] проведен при разбиении нижней части конструкции на 196 элементов, верхней – на 64 элемента. В графовом подходе верхний параллелепипед разбивается на 150 элементов, нижний – 550 элементов. На рис. 4 показаны графики напряжений σ у / р , полученные МКЭ, МГЭ и графовым методом. Заметим, что, как и в [29, 30], отсчет расстояния ведется от вершины угла, лежащего на ребре крепи.
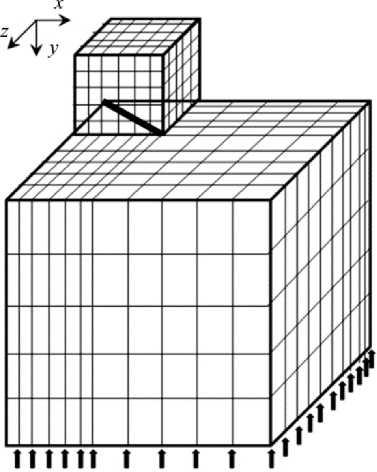
Рис. 3 Геометрия задачи
Fig. 3. Geometry of the problem
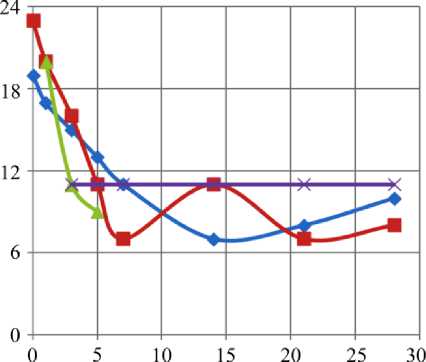
♦ графовый метод
-■- МКЭ из [30]
-*- МГЭ из [29]
-и- МКЭ из [29]
Рис. 4. Распределение напряжений σ у / р , по диагонали сечения крепи
Fig. 4. The σ у / р stresses distribution along the diagonal cross section of the lining
Как видно из графиков, результаты расчетов графовым методом согласуются с общей тенденцией распределения напряжений из [29, 30], позволяя при этом получить более точное решение.
Список литературы Уравнения состояния графовой модели трехмерных упругих тел в декартовой системе координат
- Применение теории графов связей в технике/под ред. Кэрнопа Д., Розенберга Р. -М.: Мир, 1974. -96 с.
- Ильинский Н.Ф., Цаценкин В.К. Приложение теории графов к задачам электромеханики. -М.: Энергия, 1968. -200 с.
- Кениг Г., Блекуэлл В. Теория электромеханических систем.-М.: Энергия, 1965. -424 с.
- Цветкович Д., Дуб М., Захс Х. Спектры графов. Теория и применение. -Киев: Наукова думка, 1984. -384 с.
- Басакер P., Саати Т. Конечные графы и сети. -М.: Наука, 1974. -368 с.
- Свами М., Тхуласираман К. Графы, сети и алгоритмы. -М.: Мир, 1984. -454 с.
- Крон Г. Исследование сложных систем по частям -диакоптика. -М.: Наука, 1972. -542 с.
- Крон Г. Тензорный анализ сетей. -М.: Советское радио, 1978. -720 с.
- Kron G. Equivalent circuits of the elastic field//J. Appl. Mech. -1944. -Sept. -Vol. 11. -P. A149-A161.
- Kron G. Tensorial analysis and equivalent circuity of elastic structures//J. Franklin Inst. -1944. -Vol. 238. -No. 6. -P. 399-442.
- Hetenyi M. Handbook of Experimental Stress Analysis. -Wiley, New York, 1950. -P. 789-807.
- Кузовков Е.Г. Применение метода элементарных ячеек для численного решения задач теории упругости. Сообщ. 1. Общие положения метода элементарных ячеек//Пробл. прочн. -1982. -№ 12. -С. 104-107 DOI: 10.1007/BF00768663
- Кузовков Е.Г. Применение метода элементарных ячеек для численного решения задач теории упругости. Сообщ. 2. Сетевая модель упругого тела//Пробл. прочн. -1983. -№ 2. -С. 37-43 DOI: 10.1007/BF01523469
- Кузовков Е.Г. Сетевая модель упругого тела с источниками граничных нагрузок. Сообщ. 3//Пробл. прочн. -1983. -№ 10. -С. 63-68 DOI: 10.1007/BF01523322
- Кузовков Е.Г. Конфигурация и параметры графовой модели упругого тела//Пробл. прочн. -1986. -№ 4. -С. 98-103 DOI: 10.1007/BF01524081
- Кузовков Е.Г. Уравнения состояния графовой модели упругого тела//Пробл. прочн. -1986. -№ 5. -С. 112-117 DOI: 10.1007/BF01522789
- Kuzovkov E.G. Axisymmetric Graph Model of an Elastic Solid//Пробл. прочн. -1996. -№ 6. -С. 83-103 DOI: 10.1007/BF02209319
- Кузовков Е.Г. Графовая модель упругой среды в декартовой системе координат//Пробл. прочн. -1993. -№ 12. -С. 60-70 DOI: 10.1007/BF00774638
- Кузовков Е.Г. Графовая модель упругого тела в смешанных переменных//Пробл. прочн. -1986. -№ 6. -С. 88-92 DOI: 10.1007/BF001523964
- Кузовков Е.Г., Тырымов А.А. Графовые модели в плоской и осесимметричной задачах теории упругости. -Волгоград: Изд-во ВолгГТУ, 2010. -128 с.
- Тырымов А.А. Сингулярный элемент графовой модели упругой среды в декартовой системе координат//Вычислительная механика сплошных сред. -2011. -Т. 4, № 4. -C. 125-136 DOI: org/10.7242/1999-6691/2011.4.4.47
- Тырымов А.А. Осесимметричная графовая модель упругого тела с переменным модулем упругости//Вестн. Самар. гос. техн. ун-та. Сер.: Физико-математические науки. -2012. -№ 2. -C. 103-114 DOI: 10.14498/vsgtu914
- Тырымов А.А. Численное моделирование и анализ напряжённо-деформированного состояния анизотропного массива горных пород на основе графового метода//Физико-технические проблемы разработки полезных ископаемых. -2012. -№ 5. -C. 52-66 DOI: 10.1134/s1062739148050061
- Тырымов А.А. Графовая модель упругой среды в полярной системе координат//Изв. вузов. Машиностроение. -1999. -№ 1. -С. 3-15.
- Тырымов А.А. Графовая модель трехмерных упругих тел в декартовой системе координат//Вестник Пермского национального исследовательского политехнического университета. Механика. -2016. -№ 3. -С. 282-303 DOI: 10.15593/perm.mech/2016.3.19
- Евстигнеев В.А., Касьянов В.Н. Толковый словарь по теории графов в информатике и программировании. -Новосибирск: Наука. Сиб. предприятие РАН, 1999. -291 с.
- Татт У. Теория графов. -М.: Мир, 1988. -424 с.
- Зыков А.А. Основы теории графов.-М.: Наука. Гл. ред. физ.-мат. лит., 1987. -384 с.
- Бенерджи П., Батерфилд Р. Метод граничных элементов в прикладных науках. -М: Мир, 1984. -494 с.
- Тюкалов Ю.Я. Решение объемных задач теории упругости методом конечных элементов в напряжениях//Изв. вузов. Строительство. -2006. -№ 2. -С. 19-26.


