Уравнения трехмерной модели электромагнитного поля асинхронного двигателя с поперечным потоком

Стремление эффективного использования активного объема электрической машины требует совершенствования методов их расчета, в максимальной степени базирующихся на аналитических соотношениях, позволяющих наиболее полно исследовать взаимосвязи между геометрией машины и ее выходными характеристиками. Определение дифференциальных параметров электромагнитного поля ( E , H ) во всем объеме электрической машины с учетом ее конструктивной анизотропии дает более точные расчеты.

При аналитическом исследовании электромагнитного поля в линейных асинхронных машинах используется математическая модель машины в виде совокупности сплошных ортотропных сред. Для большинства линей- двигателя с произвольным числом фаз.

магнитный поток, индукция, электромагнитное поле, ных асинхронных двигателей (ЛАД) могут быть определены следующие характерные зоны: активный слой индуктора, воздушный зазор, сплошная проводящая среды [1–3]. Размеры зон при выбранной системе координат не зависят от числа фаз моделируемой машины.

Практика создания индукционных машин показывает, что фактически во всех случаях пазы статора остаются открытыми. Дискретное размещение обмоток в открытых пазах статора создает в рабочем зазоре наряду с основной гармоникой поля также определенное количество высших пространственных гармоник [4].

С помощью модели бесконечно длинного и широкого индуктора определим характер распределения магнитного поля основной и высших пространственных гармо-

ник в рабочем зазоре. Что касается последних, то даже такая короткая машина, как двухполюсная, имеет по длине для пятой гармоники 10 полюсов, для седьмой - 14 и

т. д., т. е. для определения поля, создаваемого высшими пространственными гармониками, приближение бесконечно длинной машины оказывается достаточным.

Реальный m -фазный индуктор состоит из mn отдельных электромагнитов, где m - число фаз, n - число элементов в одной фазе. Каждый электромагнит может иметь обмотку в виде катушек, охватывающих сердечник только одного элемента (сосредоточенная обмотка), или в виде отдельных катушек, охватывающих несколько элементов (распределенная обмотка). Бегущее магнитное поле создается с помощью подключения обмотки к соответствующим фазам сети (инвертора). Количество фаз многофазных линейных асинхронных двигателей можно представить как m = m ( 5 , h ) = 2 ⁵ (2 h + 1); 5 , h = 0,1,2, _ и выделить три вида числа фаз: m (5 = 0, h * 0) - нечетное; m (5 * 0, h = 0) - четное; m (5 * 0, h * 0) - четно-нечетное. По конструктивному исполнению многофазные асинхронные двигатели делятся на симметричные и несимметричные, что определяется расположением фазных обмоток на статоре. Целесообразность введения не-симметрии объясняется следующими причинами. В общем случае двигатель может быть выполнен симметричным при любом числе фаз. Однако такое исполнение с четно-нечетным числом фаз не оптимально по пульсациям тягового усилия при несинусоидальном напряжении. Для двигателей с такими числами фаз оптимально несимметричное исполнение. Симметричное исполнение оптимально только для двигателей с нечетным и четным числами фаз.

Для индуктора с q = 1 характерно то, что токи, текущие в любых расположенных рядом элементах, различаются по фазе на постоянный угол. Этот угол, в принципе, может быть произвольным, но, поскольку ширина фазной зоны в реальных индукторах может составлять только 60,90 и 120, будем считать, что упомянутый угол сдвига фазы равен 2 п / m .

Система токов представляет собой суперпозицию из

питании симметричной трехфазной нагрузки, соединенной в звезду без нулевого провода, симметричной системой напряжений в фазных токах и напряжениях присутствуют только гармоники прямой и обратной последовательностей, составляющие класс синхронных гармоник [5].

В системах с m > 4 гармоники фазных напряжений и токов по их свойствам делятся на три класса:

• -    синхронные: n = adm + v;

• -    асинхронные: [( a - 1) dm + 2] < ( n * ac ) < ( adm - 2);

• -    сквозные: n = ac,

где d = 1 для четных m ; d = 2 для нечетных m ; c = m /2 b -целое число; a , b = 0,1,2, _; v = ± 1. Свойства гармоник

каждого класса выявляются из анализа их операторов фазовых смещений a ( n , m , k ) = 2 n n ( k - 1)/ m с учетом (2).

Для синхронных гармоник a ( n , m , k ) = v 2 n ( k - 1)/ m , откуда следует, что они имеют чередование фаз, совпадающее с прямым ( v = +1) или обратным ( v = -1) чередованием фаз на первой гармонике. То есть класс синхронных составляют гармоники прямой и обратной последовательностей, в том числе и первая. Поля, создаваемые ими, движутся в пространстве синхронно с их частотой в прямом и обратном направлениях.

Чередование фаз на асинхронных и первой гармониках не совпадают Например, в пятифазной системе чередование фаз на третьих гармониках 1-3-5-2-4. Это явление приводит к тому, что поля, создаваемые асинхрон-

ными гармониками, вращаются в пространстве в прямом или обратном направлениях не синхронно с их частотой, а на одном периоде частоты совершают более одного оборота. Синхронные и асинхронные гармоники присутствуют в спектрах при любом m > 4.

Существование сквозных гармоник возможно только при четно-нечетном m = 2 ⁵ (2 h +1) в нерасщепленных системах. Порядок этих гармоник может быть представлен выражением n = am /2 ⁵ , с учетом которого a ( n , m , k ) = = a n ( k -1)/(2 ⁵ /2). Из последнего выражения видно, что в 2 ⁵ /2 симметричных (2 h + 1)-фазных подсистемах операторы фазовых смещений отличаются на 180 ° от операторов в других 2 ⁵ /2-подсистемах. Причем во всех фазах одной

m подсистем при условии, что каждая следующая подсистема сдвинута вдоль оси x на расстояние 2 т / m и переменный ток, протекающий в относящихся к ней проводниках, сдвинут по фазе на угол 2 п / m :

m

xZ e

k = 1

2п( k - 1)( n ± 1)

wIe ^{j ω t}

A =----- x p τ

подсистемы сквозные гармоники имеют разные операторы. Эта особенность приводит к тому, что результирующее поле, создаваемое каждой сквозной гармоникой в m -фазной системе, равно нулю.

Выражение (1) можно упростить следующим обра-

зом:

m

, 1 m n ,   2 k T

⁽7 ⁺ Z ^{cos n e} x ^{( x +} —^)).

2 k = 1               m

Л = WmIe j - p τ

x ( e

m j 2 П k - 1)( n ± 1)

Множитель Z e   m в зависимости от n и m k=1

- j в x x ₊ Z ( e - j (1 - v m )в x x + e -j(1+ ^V m^№ x x )) v= 1

Как видно, разложение линейной токовой нагрузки рассматриваемого индуктора в ряд Фурье содержит про-

имеет следующие значения:

m     2 п ( k - 1)( n ± 1)

Z e m = k=1

(m ^ [ n ± 1] = am ,

= ^                         ’ a = 0,1, 2,3,....

[ 0 ^ [ n ± 1] * am

Анализ (2) показывает, что при m > 4 отдельные группы гармоник приобретают принципиально новые свойства, отличающие их от гармоник в системах m <  4. При

странственные гармоники не со всеми номерами, а только с v m -1 и v m + 1, ( v >  1). Показатель степени у экспоненты в (3) для гармоник с номерами v m - 1 отрицательный. Это означает, что данные гармоники бегут в положительном направлении оси x . Гармоники с номерами v m + 1 бегут в отрицательном направлении оси x.

Токовый слой имеет пространственно-периодическое распределение линейной нагрузки по двум взаимно перпендикулярным направлениям (рис. 1). Он распределен

синусоидально, бежит вдоль оси x и имеет синусоидальное распределение вдоль оси z .

rot H = J ,

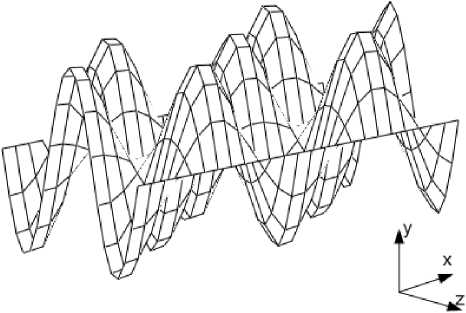
Рис. 1. Распределение линейной нагрузки

∂ B rot E =-    ,

∂ t

То есть описывается следующим уравнением:

_Δ= wmIe j ω t

_∞         p τ

_{× (} e - j β x x _{+∑ (} e - j (1 - ν m )β x x ₊ e - j (1 +ν m )β x x ₎₎cos_{β z}z _.

ν= 1

Расчетная модель линейной индукционной машины с поперечным магнитным потоком представлена на рис. 2. При построении расчетной модели приняты основные допущения: сердечник индуктора моделируется бесконечно длинной в поперечном и продольном направлениях средой с µ _–3 и ρ ₃; на поверхности сердечника расположен бесконечно тонкий токовый настил с линейной плотностью (4); система координат жестко связана с индуктором, который отстоит от электропроводного рабочего тела на расстоянии δ ; вторичный элемент представлен, как твердое тело с параметрами µ _–2 и ρ ₂ =∞ , который движется со скоростью u в направлении бегущего электромагнитного поля, создаваемого индуктором; среда 1 представляет собой воздушный зазор с параметрами µ _–1= µ _–0 и ρ ₁= 0.

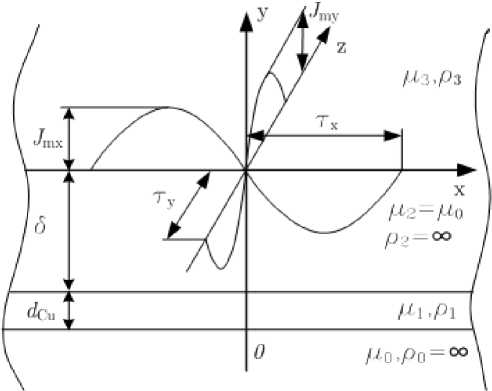
Рис. 2. Математическая модель одностороннего ЛАДПП

При заданном пространственно-временном законе изменения линейной токовой нагрузки, электромагнитное поле в любой области машины описывается уравнениями Максвелла:

div B = 0,

B = μ₀ H .

Ток определяется из уравнения J = γ E .

Вводя вектор-потенциал A , получим B = rot A .

Из (6) и (10) следует

∂ A E =-

∂ t

.

Если вектор-потенциал выбран из условия div A = 0, то из (5) и (10) получим

С² A =- μ J .

Подставляя значения J из (9) и E из (11) в уравнение (12), получим

С² A =- μ ^dA . dt

Это основное уравнение поля записано для вектор-потенциала A движущейся среды.

Скорость вторичного элемента имеет только одну составляющую по оси x , поэтому можно записать

dA ∂ A ∂ A ∂ x ∂ A ∂ A =+=+ υ .

dt ∂ t ∂ x ∂ t ∂ t ∂ x

Из уравнений (13) и (14) получим

₂       ∂ A ∂ A

∇ ² A = μ γ   + υμ γ .

∂ t ∂ x

В данном уравнении u – скорость движения вторичного элемента в направлении оси x . Считаем, что токи индуктора и вторичного элемента не имеют y -составляющей. Следовательно, можно допустить, что вектор-потенциал, обусловленный указанными токами, также не будет иметь ψ -составляющей [4; 5]

∂2A   ∂2A∂ xxx ∂x2    ∂y2

∂A∂A =μγx+υμγ

∂ t ∂ x

∂2A   ∂2A   ∂2A z+z+z=

∂ x ²     ∂ y ²     ∂ z ²

∂ A ∂ A = μγ _{∂ t} ^z + υμγ _{∂ x} ^z .

Общие решения уравнений для вектор-потенциала получим в следующем виде:

wmI

A _{1 x} ( x , y , z ) = j      μ₂ ×

2 p τ

× [^{1 U n β z} e ^∑ν= 0 β 2 n K n n β x

^{jn β xx ]} n = ν m ± 1 sⁱn^β z z ^,

wmI

A _{1 z} ( x , y , z ) =        μ₂ ×

2 p τ

∞ × ∑ [ ^{U n} e ν = 0 K n

^{jn β xx ]} n = ν m ± 1 cos^β z z ^.

Общие решения уравнений для напряженностей элек- трического поля получим в следующем виде:

wmI j ω t E = ω e ^{j ω t} μ × ^{1 x}      2 p τ²

× ∑^∞ [^{1 U n β z} e ^{- jn β x x} ] n = ν m ± 1 sin β z z , ν = 0 β_{2 n}K_nn β _x

E

∞ × ∑ [ ν= 0

wmI j ω t

- j ω      e ^{j ω t} µ ₂ ×

2 p τ

1 U n e ^β 2 n ^K n

-jnβxx n=νm±1z.

Общие решения уравнений для напряженностей магнитного поля получим в виде

1 x

∞

× [^{1 U n ∑} ν = 0 β 2 n K n

wmI j ω t μ 2 H = e

2 p τμ₁ e ^{- jn β xx} ] n =ν m ± 1 cos β z z ,

∞ × ∑ [ ν = 0

H1 =jwmIejωtμ2× y     2pτ     μ1

1 ^U n n β x ⁺β z e - jn β x x _{] β 2 nKnn β x}             n =ν m ± 1

cos β _zz ,

H 1 z =- j^wmIe ^{j ω t μ2} ×

2 p τμ₁

∞ _′

∑ [^{1 U n} e ^{- jn β xx} ] n =ν m ± 1 sin β z z ,

ν= 0 β 2 n K n

где

K n = (sh β 2 n ( a - b ) + ^{β 0 n µ 2})ch β 1 n b + ^β 2 n ^µ 0

+ ( ^{β 0 n µ 1}sh β 2 n ( a - b ) +

β _{1 n} µ ₀

+ ^{β 1 n µ 2}ch β_{2 n} ( a - b ))sh β_{2 n}b , ^β 2 n ^µ 1

U_n = ch β_{1 n}y + ^{β 0 n µ 1}sh β_{1 n}y , β _{1 n} µ ₀

• ^β 0 n ⁼ 'j n ²β _x ² + β _z ² + j ω _n μ₀γ₀,

• ^β 1 n ⁼ J n ²β _x ² + β _z ² + j ω _n μ₁γ₁ s_n ,

• ^β 2 n ⁼ V n ²β _x ² + β _z ² + j ω _n μ₂γ₂.

Для каждой гармоники будет свое скольжение, поскольку скорость распространения поля, соответствующего различным гармоникам, различна.

Для оценки линейного двигателя решающее значение имеет тяговое усилие, т. е. сила, действующая на подвижный элемент в направлении движения главного поля.

F = ∫∫∫ ( J × B ) dV .               (25)

V

Принятый метод определения дифференциальных параметров электромагнитного поля позволяет получить аналитические зависимости всех этих параметров в функции геометрии и нагрузки ЛАД с произвольным числом фаз. Результаты расчетов, выполненные для номинального режима при пересчете параметров ЛАДПП при сохранении потребляемой мощности, представлены на рис. 3.

Увеличение числа фаз приводит к улучшению качества установившихся электромагнитных процессов и ме- ханических характеристик двигателя при неизменном исполнении вторичного элемента.

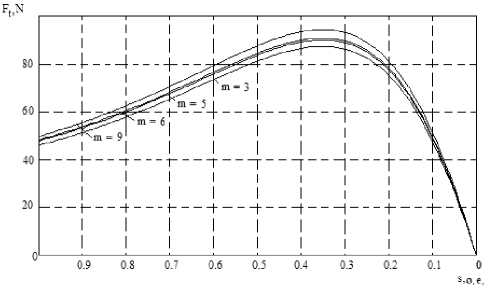
Рис. 3. Электромеханические характеристики для различных m

Тяговое усилие девятифазной машины увеличивается на 8,7 % по сравнению с трехфазной. При дальнейшем увеличении числа фаз улучшение характеристик незначительно.

Тяговое усилие создается лишь теми гармониками токов статора и вторичного элемента, которые участвуют в формировании тягового усилия, т. е. в обмене энергии между статором и вторичным элементом ЛАД. С увеличением числа фаз системы возрастает частота, а следовательно, уменьшается амплитуда как синхронных гармоник ЭДС и токов, так и пульсаций тягового усилия.

Также расщепление многофазной системы на симметричные подсистемы существенно улучшает качество установившихся электромагнитных процессов в ЛАД, так как из спектров фазных токов исключаются гармоники, кратные числу фаз в симметричной подсистеме. Исключаемые гармоники являются асинхронными (если число фаз нечетное) и сквозными (если число фаз четно-нечетное). Например, при расщеплении систем с числом фаз, кратным трем, на симметричные трехфазные подсистемы из спектров исключаются гармоники, кратные трем.