Уравнивание триангуляционной сети при измерениях углов с пренебрежимо малой погрешностью

При создании местной триангуляционной сети общераспространенными теодолитами (Т15, ТЗО) горизонтальные углы измеряются с гораздо большей точностью, чем расстояния нитяным оптическим дальномером. Так, теодолитом Т15 можно измерить угол с относительной точностью 1:(360-60-4) = 86400- = 86400 = КГ5, тогда как расстояния измеряются с точностью 1:100 L 1:300.

Рассмотрим случай, когда триангуляционная сеть состоит из цепочки п треугольников, имеющих только по две общие стороны за исключением первого и последнего треугольников, имеющих одну общую сторону (см. рис. 1). Для определенности и упрощения записи введем систему обозначений.

^—--4   5

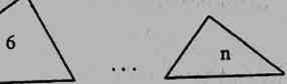
Рис. 1. Триангуляционная сеть из цепочки треугольников, имеющих по одной или две

общей стороны

Пронумеруем треугольники от первого в цепочке до последнего: / = 1 ..п, где i будет первым индексом в обозначениях углов и сторон. Углы в каждом треугольнике пронумеруем по часовой стрелке, причем первым углом обозначим угол, предшествующий общей стороне с предыдущим треугольником. В первом треугольнике цепи первым окажется угол, предшествующий единственной общей стороне. Таким образом, обозначения углов будут содержать два индекса: номер треугольника (/) и номер угла в треугольнике (/):

^“ij^J⁼ V.n,j= 1..3.

Стороны треугольника (длины сторон d), противолежащие названным углам, обозначим индексами, такими же, как и индексы этих углов:

W^, i= Т.н, j = 1..3, при этом вторые индексы у сторон в каждом треугольнике будут также увеличиваться при движении по часовой стрелке.

Истинные значения углов по условию задачи равны измеренным, а уравновешенные значения длин сторож/ обозначим в виде суммы наблюденных величин dy и абсолютных погрешностей Ду.

dy =dy + Ду. (1)

Задача заключается в нахождении таких уравновешенных значений^ (т. е., по существу, значений Д^), которые минимизировали бы сумму квадратов отклонений уравновешенных значений от измеренных, т. е. минимизировали бы сумму квадратов Ду;

» 3

Ё “* min (2) мн при условии, что все треугольники «правильные», т. е. являются замкнутыми, следовательно удовлетворяют соотношению углов и сторон по теореме синусов:

d^ j /sin и\ j = constx J = 1-3, (3) d-^ j /sin и^_а = const^ ,j = 1 -3,

- ^1,3 =

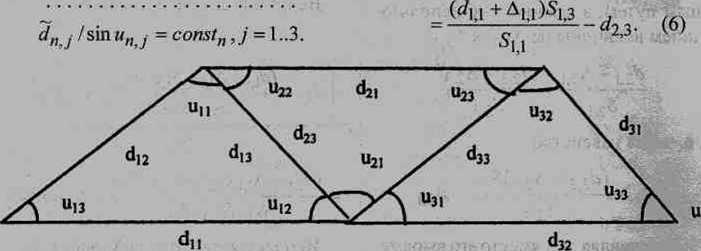
Рис. 2. Система обозначений в триангуляционной сети из трех треугольников

Равенства (3) позволяют однозначно выразить все d, у через dx ], поэтому варьирующей переменной является величина Зщ, т. е., по существу, величина А] ] в условии (2).

Выразим все Д, ■ через А₁ р Для простоты ограничимся триангуляционной сетью из трех треугольников, с надеждой обобщить полученный результат для произвольного п (см. рис. 2). Для первого треугольника по теореме синусов имеем:

51,2 _ 5ц

^1,2 SI,1

где через Sy обозначено выражение sin Uy или

d\,i +Д1,2 _ ^м + Ац

SI,2           Sl,l откуда

(ц +A_l1)S₁₂

Al,2=----ё-- ^d^2- ^

Аналогично получим

.       (^l.l + Aj.1)^s1,3    ,      ,-,

Д1,3=—--»У- (5)

51,1

Сторона d\ з первого треугольника является общей со стороной d-^ второго треугольника:

51,3 = ^у или з + Д13 = d23 + Ay откуда Д2з = dxs3 + А] з - ^2,3 •

Подставляя сюда выражение Ди из (5), получим

Л2,3 =51,3-^23 +

Mj + Ац^Ц

Далее по теореме синусов для второй стороны второго треугольника по-лучаем

А,3 _ Аз

$2,3   $2.2 ’ или

$2,2

откуда

(23 + A23)S22 д2 2 =----------с/2 2. $23

Подставляя вместо Д2 3 его выражение из (6). получим

(A.i+AyjSy  , |с

~—ё---3 $23

А) $2,3

(А1+Ац)$13'$2,2 д 1ПХ

-«2.2 =---- ё—"с-----—А²'

$U " $2,3

Аналогично для первой стороны второго треугольника:

А» А,2

$2,1    $2,2 ’

Aj + Д2,1 А.2 + Д2.2

ИЛИ ---г----=---ё--- $2,1           $2,2

откуда

(А.2 + Д2,2)$2,1   ,

А2,1 =------ё--А,1-$2,2

Подставив вместо его выражение из (7), получим д2,1 = а ,(А1+Дц)$13'$22 , L

“2.2 +-----с ё-------“2.2 $21

₌<____________ $1.1 '$23 _____________ J

$22

(Aj+Al^U'Aj'Al (^

"Al-----ё---ё--“2,1 V '

Однако Д2 j можно определить иным путем, а именно — с использованием величины не Д2 2, а Д2 3:

А.1 + А₂J _ А,3 + ^Д23

$2,1         $23

т. е. через равенство

(А,3 + А2,з)$2.1 ,

Д2,1 =------ё---------“2,1.

$2,3

Подставляя Д22 вместо его выражения из (6), получаем:

Д2Д =

(Al+Al,l)$13     )

“2,3 +--ё---------“2.3 -$2,1

$2,3

(]]+Дц)5у521

-“2,1 =--—--—--“21, (9)

$11 '$23

что аналогично (8), если указанное выражение сократить на S2 2-

Для стороны третьего треугольника, общей со стороной второго треугольника, имеем т. е.

Аз + А33 = А.2 + Д2.2 ,

А3.3 = A3 + Д23 * Аз •

Подставляя Д2 2 из (7), получим л д , (А.1 + А1.1)'$1.3‘$2.2 д33 = “2.2 +------ё---ё--

$1.1 ’$2,3

~ А.2 - ^d33 ⁼

(А.1 + А1д)$1.3 ‘$2,2    . /1ПХ

= ' ~---ё--^3- (10)

$1,1 " $2,3

Величину Д2 з определим из следующего соотношения:

А,2 ^{+ Д}3,2 _ А,3 ^{+ А}3,3

$3.2

$3,3

(Аз ^{+ Д}зз)’$зз . или Д_{3 2} =---------------- — d^ ₂.

После подстановки из (10) получим

Д3 2 = д , (^1.1+д1,1)-$1,3"$22, L

“зз + ---ё—ё--Аз г3-2

$3,3

с с с

Последнюю из требующихся нам величин, Д3 |, определим аналогично:

Al + А3.1 _ А.З + Аз,з $3,1$33

откуда

Л _ (Аз+А3,з)-$3.1 J дзд =-----ё--Ai-$з,з

Величину Д3 з подставим из (10):

А3,1 =

(А+Д1,|)"$13$23 , L “з,3 +--ё---ё--“ЗА $3.1

₌ (__________ $1,Г $23 ___________ J

$33

(А,1+А1.1)$13'$2^$3.1   ,   ..-.

=----ё-ё---ё--А1- (|2>

$1,1 • $2.3 • $3.3

Используя выражения Д/у через Д] ,, полученные в (4)—(8) и (10)—(12), най дем выражение для суммы квадратов отклонений наблюденных длин сторон от «правильных», записанное в (2). При этом следует обсудить важный вопрос: включать ли в эту сумму невязки всех сторон всех треугольников (т. е. должна ли эта сумма состоять из Зл слагаемых) или общие стороны должны входить в сумму только один раз (т. е. должна ли эта сумма состоять из Зп— (л - I) = = 2л + 1 слагаемых). Проверка показала, что верным является второй вариант, т. е. для трех треугольников сумма должна состоять из 7 слагаемых.

Итак, 1ЕД^=Дц +

/=U=1

(А1 +Д1,|)$1,2

sl,l

\2

-Аз

(А1^+Ац)$1.з д

—du

+

<А1 + Аи)‘$1,3 "$2,2

$1,1 '$2,3

- Аг

(Al^+Au)$13$2,l д

-----ё---ё--

$1,1 ‘$2,3

(^1,1 + А 1,1)- $13 ‘ $2,2 1 $3,2

,      $U"$2,3-$3,3

- А2

СА1+Дц)-$1.3 "$2,2-$3,1   , )

,       $1.1’$23’$3,3

Упрощая это выражение и раскрывая скобки в квадрате, будем оставлять только члены, содержащие А] (, так как в последующем будет необходимо брать произвольную по А] р

- *2 AAi+ai,i)2$U

L L ^д1,1 - А 1,1 +--------

<=V=i                    $1.1

2 (Al ^+A1,1)$1,2 • А² ₁

$1.1

(Ai+ Ai,i)2 -$1з

Ал

_ ₉ (^ц ^{+ A}i,i)$i3 • Аз ₊

Ал

(А,1+А1,1)*" $13 $2,2

2 (А ^{+ Д}1,1)" $13 '$2,2 ' ^2Д _[ $1,1 '$2,3

! (Ал ⁺ Ау)² -$1з -Sy $Ц • $23

₂ (4.1 + ^А1.|)'4.з 'Sy '^d2.\ Sy • 52,3

. <^1 J + ^А1Л )² ■ Sy • ^S2,2 • ^3,2 rt2 «2

41 Чз e4,3

з (4,1 ⁺ Ay) • Sy • S₂,₂ • S₃,₂ • 4,2 Sy ‘ S₂,₃ ' Sy

(4,1 ^{+ A} 1,1 )² " Sy ‘ *^2,2 " Sy n2 n2

_ з (4,1 ⁺ Ay) ■ Sy • Sy " ^3,1 ' 4,1 Sy • S₂,₃ • S33

Освобождаясь от очередных скобок, вновь оставим только те члены, ко торые содержат величину Д| ।:

(4rj4jj^Lll^LI

л 3    _

Ё Z= А1,1 +2 <=4N э Al,l 'Sy ^1,2 Sy

п(4,1 Ли + AL1)" Sy с.2 4,1

AySy-fify

4,1

, 3 (4,1 • Ay + Ay) • Sy • S_{2 2}

+ Z            c2

Sy 1Sy

₂ ^АУ'Sy-S₂y4>,2 _| Sy " S₂,₃

з (4.1 " ^Ay + Au ) • Sy • S₂j

Sy "Sy

₂ AySySyd₂₁ !

4,1 ' Sy з (4.1 - Ац + Ay)1 Sy • Sy ■ S3 2 r.2

Sy " S2,3 1 S3,3

т ^AU '4,3 ’S₂,₂ '-4.2 '4,2 ₍

4,1 ‘Sy ’Sy

3 (4,1" Ay +Ay )² " Sy ¹ 82,2 ^- Sy six-sb-sb

-, Ay 'Sy ‘Sy S3I '4,1 SU ' Sy • S33

Возьмем производную этого выражения по Д, । и приравняем ее к нулю, предварительно опуская постоянную 2:

S1.2 " 4,2 _| 4,1 ' Sy ASy

4ц Sy Sy

_ Sy "4,3 ₊ 4.1Sy 'Sy ₊ ASy - Sy _ Sy     Sy • Sy    Sy • Sy

4,3'Sy 4,2 ! 4,|Sy-S₂,i !

Sy-Sy Sy-Sy

! ASy 'S₂,| S₁₃ -S₂ , 4 _a Sy-Sy Sy Sy

! 4,lSy Sy- Sy ! ASy -Sy -Sy Sfi • Sy • S33 Sy • Sy • S33

Sy • S^₂ • S3 ₂ • d_{3 2 (} Sy -S₂₁3 Sy

! 4jSy-Sy-Sy ASy-Sy-Sy q2 r»2              q2 гт2

Чг⁵23 -^33   Чг^З’^ЗЗ

_ Sij • Sy • s₃₁ • ₃₁ Sy - Sy - Sy

Группируя отдельно члены, содер-aaai ёа d_x ] и А, получим

Д + 4 ] • А + АЛ - В = О, с2    с2     о2 г<2

о12  Ду  оу»2,2

где ^л - „2 ⁺ г.2 ⁺ г,2  с.2    ,

41  Sy  Оу-Оу о- о2 о2 г.2 с. 2 ^IJ/Sy О|з -Ьу -Ду q2 г.2 + с.2 с2 с.2  +

44,а2,3 Sy-Оу-Ду с.2 о2 с2 (    - Ду - Ду п2 о2 п2 . д1.1 1 Sy • Д3.3

«L2+-7--4,3 +

I Sy Ду

Sy Sy    Sy Sy

--a2 э 3---Дэ I +

Sy Sy     Su-Sy

SyS2,2-S3 2

--d3i +

4j-S2,3-s3,3 3’2

4,з ~s2,2 - Sy

4.1 -s2i3 Sy

•4,1 =0-

Отсюда оптимальное значение Ay = Д будет равно

B-dVJ.A

Д11 =----------

1 + A

Простейшую проверку правильности решения сделаем, рассмотрев три равносторонних треугольника, пртем такие, в которых наблюденные длины сторон равны, т. е. измерены без погрешностей. Если решение (14) верно, то должно получиться Д] |=0.

Подставляя в А и В значения 4 1 = 1

и Sy = const =    . получим А = 6,

В = 6, откуда

64 j-^dt у

Ди = — ---— = 0.

м 1 + Л т. е. проверка подтвердила правильность решения.

Более суровая проверка заключается в рассмотрении цепочки из прямоугольных треугольников, сочлененных, как показано на рис. 3.

Составим таблицу синусов углов и длин сторон для этого случая: (d₍₎ равно диагонали треугольника).

Подставим эти значения в В и А.

11 1 73 73

B = ¹¹ ₊ 2 ' 2 ₊ 2 ' 2 ' 2

73 73

1    1311

1 ' 1

. _2_______. 2 2 2 2 .

7з 1 7з 1 73

2 ' 2      2 ' 2 ' 2

2 к 7

4 ' 4

Г 3 f. 1

2     4

к 7

+

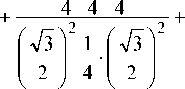
и

+

Подставляем эти значения в (14):

^А 1,1 =

B — d 11' A 1 — A

= 0 ^

= 17^ — 1^ = о

23 23   ^,

что и требовалось доказать, т. е. значение ∆ _1,1, удовлетворяющее условию наименьших квадратов отклонений из-

меренных длин сторон от истинных, определяется равенством (14).

Для урaвнивания триангуляционной сети такого типа составлены алгоритм и программа на языке Турбо Паскаль-7.