Урунинг параболик элемент атрофидаги аракати ва элемент параметрларини анилаш

Барабанли қобиқлаш ускунасида қобиқлаш процесси яхшиланиши учун унинг ички цилиндрик айланма сиртига параболик элементлар маҳкамланиб чиқилади. Бу ҳолатда айлана бўйича ҳаракартланаётган уруғ элементга келганда ҳаракат йўналишини ўзгартиради, яьни у аввал қиялик бўйича юқорига кўтарила бошлайди ва юқори нуқтасига чиқиб ёки чиқмасдан параболик юзада сирпаниб чиқаётиб ўнг ёки чап томонга айланма ҳаракат қилиб ағдарилиб тушади. Шу пайтда уруғнинг барабан сиртида ишқаланиб келаётган, яьни химикатлар билан бўланиши қийинлашаётган пастки томони бўланиш имкониятига эга бўлади.

1-расм. Параболик элемент ва унинг параметрлари.

1-расмда параболик элемент параметрлари билан кўрсатилган. Бундай элементлар барабан ички сирти бўйича шахмат тарзда маҳкамланган. 2-расм.

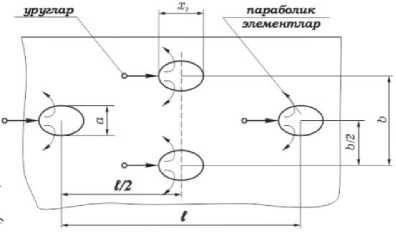
2-расм. Параболик элементнинг барабан ички юзасида жойлашув схемаси.

Барабаннинг радиусига нисбатан уруғнинг ўлчами жуда кичкина бўлгани учун О нуқта атрофидаги кичик узунликни текис юза деб ҳисоблаб, уруғнинг ҳаракатини шу он учун тўғри чизиқли ҳаракат деб қабул қиламиз.

Уруғни бир моддий М нуқта деб ҳисоблаб, у қандайдир О нуқтадан горизонтга α бучак остида Vo бошланғич тезлик билан ирғитилган деб қабул қиламиз. m массали М нуқтанинг ҳаракатини ўрганамиз. 3-расм.

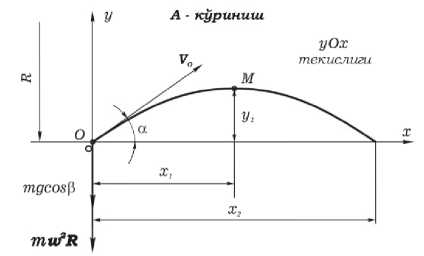
3-расм. Моддий нуқта, яьни уруғнинг ҳаракат траекторияси.

М нуқтага G оғирлик кучининг ташкил этувчиси mgcosβ дан ташқари марказдан қочма куч mω2R таъсир қилади деб унинг ҳаракатини ўрганамиз. О нуқтани координата боши деб оламиз, X ўқини горизонтал бўйича ўнга йўналтирамиз, Y ўқини эса вертикал бўйича тепага. Нуқта ҳаракатининг дифференциал тенгламасини ёзамиз.

mdx = 0  (1)            md2y = - mg cos в - ma2 R(2)

dt2

Тенгликни m га қисқартирамиз

—x = 0   (3)              —= - g cos fi - a2 R(4)

dt2

dx

(3) ни интегралласак dt

Координата ўқларига тезлик проекцияси тенгламасига биноан dx

Vx == dt

М нуқта тезлигининг X ўқига проекцияси хар доим бир хил катталикка эга булади       c = vx = v0 • cos a

(5) ва (6) тенгликлардан оламиз

Бу тенгламани интегралласак

dx

= v •cos a dt 0

x = v_ot • cos a + c₂

Агар t =0, x = 0 бўлса, у холда ўзгармас сон c 2 = 0

Охирги натижа

x = v_ot • cos a              (7)

(4) ни интегралласак

v„ = — = -gt cos в - ю2Rt + с y dt                            3

Бу тенгламага t = 0 ни қўйсак, c ₃ интегралл доимийсини топамиз.

dy

C 3 = v_v = V o • sin a демак — = v ₀ sin a - gt cos в - a Rt яна бир интегралласак

3     y    0                         _dt     0

. •       gt2          a2 R. , y = vot sin a —— cos в--— t + c4

Агар t = 0, y = 0 бўлса ихтиёрий ўзгармас сон c ₄ = 0,

Натижада

gt ²     _n  a² Rt ²

y = v_ot sin a —— cos в--——

Шундай қилиб горизонтга нисбатан α бурчак остида йўналтирилган v ₀

бошланғич тезликка эга бўлган М нуқтанинг ҳаракат тенгламаси x = vot • cos a

gt        a Rt y = vot sin a —— cos в--——

М нуқтанинг траекториясини аниқлаш учун тенгламалардан t ни йўқотамиз; (7) тенгламадан t ни топиб t = x

( v ⋅ cos α )

Уни (8) га қўямиз ва траектория тенгламасига эга бўламиз gx2 ⋅ cos β    ω2Rx2

y = x ⋅ tg α -           -

(2v2 cos 2 α)  2v2 cos2α gx2 ⋅ cos β- ω2Rx2

= x ⋅ tg α -

= x ⋅ tg α -

2v2cos2α x2 ⋅ (g cos β-ω2R)

22    ;

2 v cos α

М нуқтанинг траекторияси вертикал симметрия ўқига эга бўлган параболадир. М нуқтанинг учиш вақтини (давомийлигини) топиш учун (8) га y = 0 қийматини қўямиз. У ҳолда тенглама қўйидаги кўринишга келади:

2 gt v t sinα-    ⋅cosβ

-

ω ² Rt ²

2 ⁼

v t sin α -

( - g ⋅ cos β - ω ² R ) t ²

Бу ердан ордината нолга тенг

ҳолатидаги вақтнинг иккита қийматини

топамиз

t ₀ = 0,    t ₂ =

-

2 v sin α

( - g ⋅ cos β - ω ² R )

Вақтнинг биринчи қиймати учишнинг бошланишига, иккинчиси охирига тўғри келади. Учишнинг давомийлиги t -t = t =

-

-

2 v sin α g ⋅ cos β - ω ² R

Уруғ учиш узунлигини топиш учун ҳаракат тенгламаси (7) га t ₂

қийматини қўямиз x = v t cos α = ^{( v 0 cos α ⋅ 2 v 0 sin α )}   ёки x =    ^{v 02 sin 2 α}    (10)

^{2   0 2}          ( - g cos β - ω ² R )            ²   ( - g cos β - ω ² R )

Бу тенгламадан кўриниб турибдики, учиш узунлигининг максимал

қиймати Xmax га sin 2α = 1 бўлганда, яъни α = π/4 бўлганда эришилади xmax

v 0²

( - g cos β - ω ² R ) ^;

М нуқтанинг энг катта баландлигини аниқлаймиз, бу

ҳолатда ордината ўқига нисбатан унинг тезлик проекцияси нолга тенг

бўлади. ^y = v = v sin α - ( - g cos β - ω ² R ) t = 0

dt ^{y 0}

Тенгламадан t1 ни аниқлаймиз t = v sinα      t

( - g cos β - ω ² R )  2 ^;

Кўриниб турибдики энг катта баландлик вақт давомийлигининг ярмида эришилади x = x2 ; t1 нинг қийматини (8) га қўйсак v0 sinα⋅ v0 sinα)  (-g cos β -ω2R)v02 sin2α y1  (-g cos β- ω2R)     2(-g cos β- ω2R)2

v sin α

Бу ердан     y 1 =      ⁰          ;                                         (11)

2( - g cos β - ω ² R )

Тенгламадан кўринадики, нуқта максимал баландликни sin α = 1 ёки π /2 рад да забт этади, яъни нуқта вертикал тепага йўналганда _{y =}     ^{- v} 0 ²    _;

^max 2( - g cos β - ω ² R )

Қобиқлаш ускунаси ичида бўланиш процесси сифатли ўтишида параболик элементнинг параметрлари ахамиятга эга. Элемент баландлигини (11) билан узунлигини (10) билан аниқлаш мумкин. Уруғлар ҳаракатига элементлар тескари таъсир кўрсатмаслиги яъни кетма-кет келаётган уруғлар қияликка келиб ортиқча қаршиликка учраб тирбандлик ҳосил қилмаслигида қиялик бурчаги ахамиятга эга. Чунки унинг катта қийматларида кетма-кет келаётган уруғларнинг ортиқча қаршиликка учрашига олиб келади. Бу эса ортиқча ишқаланиш кучлари яъни уруғлар ўртасидаги ишқаланиш кучининг ортиб кетишига, уруғ сифатининг пасайишига олиб келади.

Амалда қобиқлаш ускунаси ичида уруғлар бир қанча қатлам бўлиб ҳаракатланади. Элементга келиб урилган бир неча қатлам ҳам унга теккандан сўнг қандайдир бурчакка айланма ҳаракат қилишга мажбур бўлади. Элементлар шахмат тарзда жойлашганликлари учун уруғлар биринчи элементдан айланма ҳаракат олган бўлсада кейингисига келиб яна айланади ва ҳакозо. Бу ҳолат уруғларнинг яхшироқ бўланишига олиб келади.

ФОЙДАЛАНИЛГАН АДАБИЁТЛАР РЎЙХАТИ: