Усиление микроволнового поля в полупроводниковых сверхрешетках

Полупроводниковые сверхрешетки привлекают к себе большое внимание благодаря потенциальной возможности использования их в качестве генератора и детектора терагерцевого электромагнитного излучения (0,3— 10 ТГц) [8; 11]. Необходимость в таких устройствах вызвана быстрым прогрессом терагерцевой науки и технологии в различных областях знаний [5]. Классические работы [2; 4] стимулировали большую теоретическую активность, посвященную нелинейному взаимодействию высокочастотного электрического поля с минизонными электронами СР. В этих работах было показано, что нелинейные свойства СР дайт возможность генерации ТГц-излучения в области отрицательной дифференциальной проводимости (ОДП). Одним из наиболее интересных предложений было использовать частотное умножение для генерации высокочастотного излучения [3; 7]. В то же время система является нестабильной к формированию высоко- и низкочастотных доменов в этом режиме [1]. В результате домены могут сильно подавить усиление на ТГц-ча-стотах или сильно уменьшить эффективность усиления в сравнении с предсказаниями теории.

Следовательно, необходимо так модифицировать классическую схему блоковского осциллятора, чтобы избежать возникновения доменов

' Работа поддержана грантом Президента России для молодых кандидатов нарк (МК-4804.2006.2)

(или подавить уже появившиеся электрические домены), но при этом сохранить усиление. Чтобы избежать эффектов, связанных с ОДП-не-стабильностями, мы предлагаем использовать переменное поле накачки вместо приложенной постоянной, разности потенциалов и рассматривать усиление на гармониках накачки. Сильное переменное поле в этом случае при определенных условиях подавляет нестабильности волн пространственного заряда (ВПЗ) внутри сверхрешетки и в тоже время является источником энергии для генерации и усиления гармоник. Детальный анализ этой схемы дан в [10], где было показано, что квазистатическое поле накачки может полностью подавить домены в СР.

Однако домены могут возникать в СР и в чисто переменном поле в динамическом случае благодаря нестабильности системы к малым флуктуациям постоянного поля. Причина этого лежит в создании горячих электронов с отрицательной эффективной электронной массой. В нашем случае необходимое условие формирования доменов в СР такое же, как и условие абсолютной отрицательной проводимости (ДОП) с произвольно малой приложенной разностью потенциалов. В этом случае регионы усиления шире, чем регионы ОДП, и мы можем использовать эту схему блоковского осциллятора для усиления ТГц-излучения. Интерес к данной теме возрос благодаря недавним экс-

пернментальным результатам, касающимся генерации микроволнового излучения в СР, в частности, наблюдалась третья гармоника накачки частотой 100 ГГц [9].

Итак, в данной работе мы рассматриваем СР под действием электрического поля

• Е0)    = Е₀ + Ei cos(ш/) + Е₂ cos(cu,r), (1) где Е_ц —постоянное электрическое поле (£₀< <£,), £_р = £,(costo/) — поле накачки и E_pr = £₂ (cosd^Z) — пробное поле. Заметим, что в реальных условиях пробное поле является модой резонатора, настроенного на желаемую ТГц-частоту.

Решение уравнения Больцмана для случая дихроматического поля. В этой главе мы представляем точное решение уравнения Больцмана для случая бихроматического поля (1). Мы используем стандартное приближение сильной связи для дисперсионного соотношения электронов, принадлежащих к одной минизоне:

■ Щ)-|

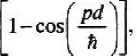
где Д — ширина минизоны; d — период сверхрешетки; р — квазиимпульс.

Уравнение Больцмана допускает точное решение. В результате мы получим синус Kia)^ и косинус /(to₂) компоненты тока. Мы определяем компоненты тока в СР под действием пробного поля как:

У(ш,) = 2<7 V(z)cos(to,r) _f = — jv(r)cos(tp,r)A, (3) К^") = 1q V (r)sin (a>,r) — ?^ J V (г)5т (оо₂т )сз7 , (4) где q = -е — заряд электрона; И?) — мини-зонная электронная скорость, усреднение (...), проводится по времени; и Т = 2 р / ш_г = = 2р/со, — общий период пробного поля и поля накачки.

Ниже мы везде пишем ток в безразмерных единицах / -qV_Qn_Ql J 21₆, где V₀=M/2h — максимальная скорость электрона в минизоне; п_е — электронная плотность; I_m — модифицированная функция Бесселя аргумента Д/2Т; Т, — решеточная температура.

Косинус компонента тока описывает генерацию и усиления тока в СР:

7= х £м^шр^х^^

i1Jl=-**V,=-*

,                              (5)

г         \1   (^0 ⁺ ^ + Z, O2₃)t__

', '^^      1 + (Йо + Z,^ + Z3ctK )2 т2

Синус-компонента тока отвечает за его фазу

К- X X Л №)А №)А™_: (&)[Л-(^*Щ-№)~ /_г J_;=-e*V_!=-*=

1                  (6)

-Л+.^И)]^;-—

В выражениях (5) и (6) Q^-qdE^/h — блоковская частота; р. = Й/ш., Й_г= qdE./h, 1= = 1,2. Заметим, что синус-компонента тока равна нулю в квазистатическом пределе y,_r<< 1 (т — время релаксации).

Рассмотрим малосигнальное приближение Е>>Е2 В этом пределе необходимо взять только определенные комбинации функций Бесселя в (5) и (6). В результате получим выражение для поглощения в виде суммы трех слагаемых j =jh°""

+ ^(Л™" + А"^)

Здесь j^harm является функцией только поля накачки и дает главный вклад в общий ток в малосигнальном приближении. Слагаемое Е¹¹™ является по сути просто выражением для /и-й гармоники тока через сверхрешетку.

",= £д(д)[^(д)+

а.-№)]т-т—"4-т

-Ч-ЦМ'А) т-

Слагаемое A^coh описывает параметрическое усиление пробного поля благодаря когерентному взаимодействию полей накачки и пробы

^'SawV.^M)-

-Г (R 'll - ^° ⁺ ^1)-~ ''^^№^1 ₊ (й_{о +} /_|Щ|)²т²

а слагаемое Д™^ссН описывает непараметрические эффекты;

ВЕСТНИК Мордовского университета ] 2007 | № 3

Д"""^ ДО)

(Q,,+ Дц -й^)т 1 + (й₀ + Цо, -а^^ т^г

_JS^±^A±^1L_ 1 + (52_О + /,0), +ах,)²т²

Важно заметить, что Л'"гаА играет существенную роль в стабилизации нестабильностей волн пространственного заряда в СР и описывает поглощение излучения свободными электронами. В пределе слабых полей Л™оЛ переходит в хорошо известную формулу Друде.

Рассмотрим далее случай нулевого постоянного поля Е_о = О.В этом случае:

/'--[1-ИГ]£ ^.(A)A™(A)t-&- (И)

Из формулы (11) следует, что /^А"” - 0 для четных гармоник. Следовательно, генерация четных гармоник запрещена и ток в СР возникает только благодаря параметрическому и непараметрическому взаимодействию полей накачки и пробы. Усиление (поглощение) определяется конкуренцией Л™" и Д^,лсоЛ₁ которые имеют следующий вид при Е_о = 0:

Л"*- ЁА(Ш-».(А)_т-&т

л^,= ^(д) 1

Некогерентная и когерентная компоненты поглощения определяют линейный отклик системы на действие внешнего пробного поля. В виду этого сумма данных компонент непосредственно связана с дифференциальной проводимостью oVttx) = — (А™*1+А'"™'1 А

Хорошо известно, что коэффициент поглощения пропорционален действительной части проводимости:

а (й),) =

4л Re ст ((У,) C-Je

где г — действительная часть диэлектрической проницаемости; с —- скорость света.

Следовательно, сумма когерентной и некогерентной компонент тока связана коэффициентом поглощения следующим соотношением

а(а)Л = ^ — ( А™'¹ + А'™⁶)        (¹⁶)

■ 2щ с v            ;

где о)_р - ^Але"»^ /еЬ — плазменная частота.

Напомним, что интенсивность света связана с коэффициентом поглощения следующей формулой:

/ (Е₂Уе-^,                      (17)

где Е^ — пробное поле, L — длина СР.

Из (17) видно, что при а < 0 возникает усиление. Заметим, что из-за малости L усиление также является слабым. Однако мы можем использовать резонатор, чтобы увеличить усиление. В этом случае волна много раз отразится и путь в (17) может быть большим. Это ведет к усилению гармоник. Детальный анализ этой схемы лежит за пределами цели данной работы.

Усиление гармоник. Рассмотрим более детально коэффициент поглощения. На рисунке (1) показана зависимость коэффициента поглощения от частоты поля накачки. Видно, что в довольно широком интервале частот поглощение отрицательно, а значит, мы имеем усиление излучения.

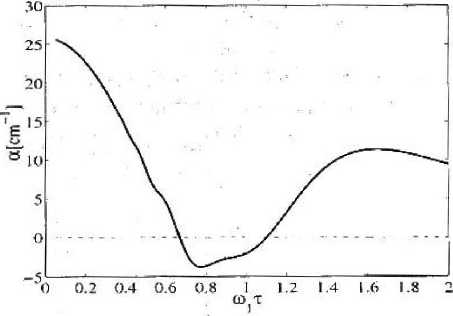
Рисунок /                       1

Усиление 4-й гармоники            !

Для вычисления коэффициента поглощения I частоты мы рассмотрели GaAs/AlAs СР с периодом d = 6,2 нм и шириной минизоны А = 24,4 мэВ. Максимальная скорость У_о = 1,5 107 см/с, концентрация электронов n₀ = 24016 см³, Заметим, что в малосигнильном приближении коэффициент поглощения для нечетных гармоник на порядок величины больше, чем для четных.                                '

Выше уже было отмечено, что поглощение может разрушаться в области АОП благодаря малым флуктуациям постоянного тока. Игнатов и Романов показали [7], что если электроны находятся под действием поля Е (t) = Е_о + E^cosw,/) , то постоянная составляющая тока в случае £₀<<  Е₍ имеет вид:

ет никаких нестабильностей, связанных с АОП. В случае же, если взаимодействие электронов с сигнальным полем динамическое, то регионы АОП могут разрушать усиление. Однако, замечательно, что регионы усиления шире, чем регионы АОП, и мы можем одновременно достичь усиления и избежать нестабильностей, связанных с АОП.

« = 3^=^

^(Д) + 2^

1-^т2 (l-T/^T2)1

Из формулы (18) видно, что вблизи нулей функции Бесселя и, следовательно, постоянный ток может быть отрицательным. Первый нуль возникает в окрестности точки р, = 2,41. Следовательно, в этом случае возникает АОП, так как существует ток электронов в направлении противоположном приложенному полю. Что, в свою очередь, означает возникновение нестабильностей в СР. Заметим, что существование АОП связано с существованием отрицательной электронной массы в СР. Если мы вычислим среднюю энергию электрона в СР, то получим:

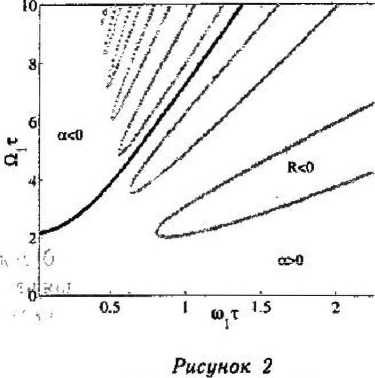
Регионы АОП и усиление 3-й гармоники

вблизи нулей функции Бесселя. В этом случае мы имеем «горячие» электроны, потому что электронное распределение сильно неравновесное и они не имеют времени, чтобы релаксировать вниз минизоны. Рассматривая флуктуацию энергии (^(р)) + ^, мы получим для электронной массы /п((е(р)) + 5р)<0 при Уо2(Д) = О. Следовательно, АОП обусловлена отрицательностью электронной массы. Физически это означает, что горячие электроны ведут к АОП и спонтанной генерации постоянного тока. В результате система является нестабильной к малым флуктуациям тока. Возможно, этим объясняется отрицательный результат в попытке наблюдать АОП в рамках минизонного транспортного режима.

Выше было отмечено, что благодаря нелинейному характеру минизонного транспорта возможно получить усиление гармоник поля накачки, если коэффициент поглощения пробного поля отрицателен. В [10] было показано, что если поле накачки квазистатическое, то не существу

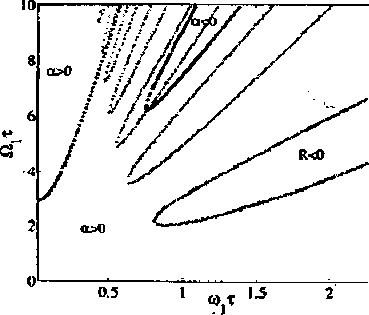
Рисунок 3

Регионы АОП и усиление 5-й гармоники

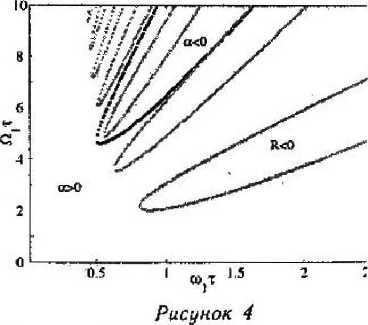
Регионы. АОП и усиление 4-й гармоники

ВЕСТНИК Мордовского университета | 2007 | № 3

На рис. 3 и 4 показано сравнение областей усиление нечетных гармоник и регионов АОП. регионы с а < 0 соответствуют усилению п-й. Регионы, где J? < О соответствуют АОП. Заме» ТиД что.регионы.усиления уменьшаются с рос- . том номера гармоники. Видно, что в квазиста-тическом пределе не существует никаких нестабильностей.

Для четных гармоник хорошо известно, что их генерация запрещена благодаря симметрии системы, однако четные гармоники могут возникать благодаря спонтанным произвольно малым флуктуациям внутреннего поля. Это ведет, в свою очередь, к возникновению внутри СР малого постоянного поля, которое разбивает симметрию системы и разрешает генерацию четных гармоник. В этом случае следует считать, что пробное поле является флуктуацией внутреннего поля и, если мы облучаем СР только полем накачки, мы должны на выходе полу чить малый сигнал четных гармоник. Чтобы определить усиление, мы должны измерить" чет-ные гармоники в режиме АОП вблизи границу усиления' и затем измерить их В регионе усиления-при слегка сдвинутой амплитуде накачки. Разница- между этими двумя измерениями даст коэффициент усиления.

Важно отметить, что усиление четных гармоник является одним из видов параметрического резонанса [11]. Заметим, что параметрический резонанс является эффектом, связанным с нестабильностью резонансной системы. Достаточно бесконечно малого возмущения, чтобы вызвать резонанс. Параметрический резонанс в нашем случае обусловлен периодической зависимостью электронной массы от энергии. Регионы усиления четвертой гармоники показаны на рис. 4. Заметим, что ни при каких условиях невозможно усиление второй гармоники.

Поступала 14.03.0/.