Усиление обратного эффекта Фарадея в диэлектрических дифракционных решётках с волноводным слоем

Магнитооптический обратный эффект Фарадея (ОЭФ) имеет место, когда свет с круговой поляризацией, падающий на кристалл, индуцирует магнитный момент М. ОЭФ был впервые предсказан Л. П. Питаевским в 1961 году [1]. В последнее время данный эффект вызывает всё больший интерес для практических применений. В частности, в работе [2] была показана возможность изменения намагничен- ности среды короткими лазерными импульсами пикосекундной длительности. ОЭФ также может быть использован для генерации фемтосекундных импульсов тока [3].

Если среда освещается поляризованным светом, величину ОЭФ (т.е. величину индуцированного магнитного момента) можно записать в виде

Из (1) также следует, что величина ОЭФ зависит от постоянной Верде. Для парамагнитной среды она может быть вычислена с помощью выражения V = 4 л ² // п X , где n - показатель преломления, х характеризует величину обычного (прямого) эффекта Фарадея и определяется формулой х = g /4 п H , где g - гиротропия среды, H – внешнее магнитное поле. Таким образом, для получения большого по величине обратного эффекта Фарадея необходимо использовать материалы, постоянные Верде которых имеют большие значения [4], или добиться максимально возможного усиления величины m = |lm ( E х E * )| за счёт использования дифракционных структур со специальным образом выбранными геометрическими и материальными параметрами. В этом отношении перфорированные плёнки обладают большим потенциалом [5].

В работе [6] исследовано усиление обратного эффекта Фарадея в металлодиэлектрических дифракционных структурах, в которых могут возбуждаться поверхностные плазмон-поляритоны. Показано, что при возбуждении поверхностных плазмон-поляритонов падающей волной с круговой поляризацией ОЭФ в таких структурах локально усиливается в 10-50 раз в областях с характерными размерами порядка нескольких десятков нанометров.

В настоящей работе на основе моделирования в рамках строгой электромагнитной теории дифракции исследуется усиление обратного эффекта Фарадея в ближнем поле диэлектрических дифракционных структур с двумерной периодичностью, состоящих из дифракционной решётки и волноводного слоя.

• 1.    Геометрия структуры и теоретическое описание

Геометрия рассматриваемой структуры, состоящей из диэлектрической дифракционной решётки с двумерной периодичностью и диэлектрического волноводного слоя, представлена на рис. 1.

И'              к           Е,„;„

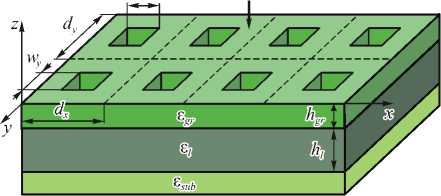
Рис. 1. Геометрия структуры

При определённых условиях, обеспечиваемых выбором геометрических и физических параметров структуры, в ней могут возбуждаться квазиволно-водные моды, близкие по структуре поля к модам плоскопараллельного волновода [7-10]. В работах [9, 10] показано, что возбуждение мод может сопровождаться существенным увеличением интенсивности (квадрата модуля) электрического поля в области подложки и формированием интерференционных картин высших затухающих порядков дифракции с периодом, в 4-6 раз меньшим периода используемой дифракционной решётки. При этом для структур с двумерной периодичностью интенсивность в ближнем поле может в 20-50 раз превышать интенсивность падающей волны.

Получим приближённые выражения для величины m и интенсивности электрического поля I в области подложки, предполагая, что при нормальном падении волны с круговой поляризацией дифракционными порядками с номерами (±n,0), (0, ±n) в структуре возбуждаются квазиволноводные моды, близкие по структуре поля к модам плоскопараллельного волновода. Рассмотрим случай, когда эти моды имеют поляризацию, близкую к TE-поляризации. Таким образом, будем учитывать только y-компоненту электрического поля для мод, распространяющихся вдоль оси Ox и x-компоненту для мод, распространяющихся вдоль оси Oy. Тогда электрическое поле, соответствующее прошедшим затухающим порядкам дифракции в случае симметричной структуры (при dx = dy = d , wx = wy = w), бу- дет иметь вид

E y , n ,0 = T n ,0 exp (^- i ^Ю t ) exp ( ik n x ) exp (^K n z ) ,      (3)

Ex,0,n = T0,n exp (-iЮt) exp (ikny ) exp (Knz), где kn = 2Лnd , Кn = kk^ - k26sub , k0 = 2пД , X -длина волны в свободном пространстве. В случае симметричной структуры и круговой поляризации падающей волны имеют место следующие соотношения между комплексными амплитудами поряд- ков: Tn,0| = T-n,0! = T0,n| = T0,-n| [11,12]- Кроме того, если в рассматриваемой структуре квазиволновод-ные моды, распространяющиеся вдоль осей Ox и Oy, возбуждаются только TE- и только TM-компонентами падающей волны соответственно, разность фаз между возбуждаемыми модами будет равна разности фаз между компонентами падающей волны. В случае круговой поляризации разность фаз составляет л/2, таким образом, будут выполняться равенства Tn,0 = iT0,n, T-n,0 = iT0-n. Справедливость такого предположения была показана в работе [13] для структур, состоящих из диэлектрической дифракционной решётки и металлического слоя. С учётом приведённых выражений амплитуды порядков можно представить в виде

T n ,0 = ^iT 0, n = ^T ± n exp ( i ф ) ,

T-n,0 = iT0,-n = T±n exp (-iф), где

^T ± n = T n ,0 1 exp ^[ i { arg ( T n ,0 ) ⁺ arg ( T - n ,0 ) } /2 ] , Ф = ^{[ a}rg ( T n ,0 ) ^{- a}rg ( ^T - n ,0 ) ] /2 ( mod ^2п) -

Подставляя полученные представления в (3), запишем выражения для компонент электрического поля суперпозиции порядков дифракции:

E y , ± n ,0 = E y , n ,0 ⁺ E y , - n ,0 =

= 2 T ± _n exp ( - i ю t ) cos ( k_nx + ф ) exp ( к _nz ) , E x ,0, ± n = E x ,0, n ⁺ E x ,0, - n =

= - 2 iT ± _n exp ( - i ю t ) cos ( k_ny + ф ) exp ( к _nz ) -

Подставляя (4) в (2), получим выражение для величины m :

m (x, z) = 8 T± n |2 |cos (knx + ф) cos (kny + ф)|х xexp(2k nz).

Интенсивность электрического поля при этом будет иметь вид

I ( x , z ) = 4 T ± n |² [ cos ² ( k n x + ф ) + cos ² ( k n y + ф ) ] x x exp ( 2 k _nz ) -

Из выражений (5), (6) следует, что распределения величин m и I периодичны по x и y c периодом d 2n . Найдём положения максимумов интенсивности электрического поля и величины m. Полагая Ф = 0, легко показать, что максимумы обеих вели- чин совпадают и находятся в точках

<

d

• x, =      l , l е Z ,

0.6

l 2n yk = ^k, k е Z-2n

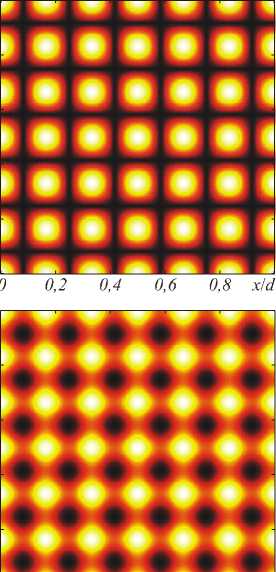
На рис. 2 показаны теоретические распределения (5), (6) в пределах одного периода решётки при z = 0 и n = 3 .

ykl

0,2

0,4

0,8

1,0

• а)

0.2

у/d

0,4

0,6

0,8

• I .O X'W 2^ '■' "W "w; v

• б)

• 2.    Результаты моделирования

Рис. 2. Теоретические оценки вида распределений величины m (а) и интенсивности электрического поля I (б) в подложке на границе раздела волноводный слой/подложка на одном периоде решётки при возбуждении в структуре квазиволноводных мод

TE-типа при n = 3

Ещё раз отметим, что полученные выражения являются оценками, не учитывающими вклад дифракционных порядков с номерами, отличными от ( ± n ,0 ) , ( 0, ± n ) и предполагающими ТЕ-поляризацию возбуждаемых мод. Для их проверки необходимо на основе электромагнитной теории дифракции рассчитать распределения интенсивности поля и величины m , формируемые рассматриваемой структурой.

Для моделирования дифракции света и построения распределений электромагнитного поля в периодических дифракционных структурах необходимо использование специальных численных методов решения уравнений Максвелла. В настоящей работе результаты численного моделирования дифракции в структуре на рис. 1 получены с помощью метода Фурье-мод (в англоязычной литературе – rigorous coupled-wave analysis) [14].

При численном моделировании предполагалось, что на структуру падает нормально волна с круговой поляризацией и длиной волны 442 нм. Для моделирования выбраны следующие значения материальных параметров структуры: е super = 1,69, еgr = еl = 4,41, еsub = 2,56 (рис. 1). Период дифракционной решётки был выбран равным 660 нм. Ос- тальные геометрические параметры структуры, приведённые в подписи к рис. 3, найдены с помощью оптимизационной процедуры из условия минимизации критерия, представляющего отличие расчётной интенсивности электрического поля от теоретической оценки интенсивности (6) при n = 3 [9,10]. Отметим, что минимизация указанного критерия также обеспечивает близость распределения величины m к теоретической оценке (5).

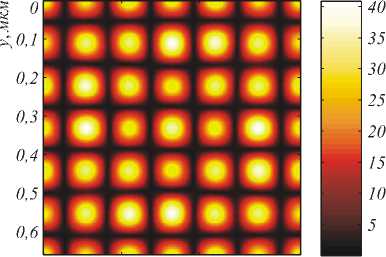
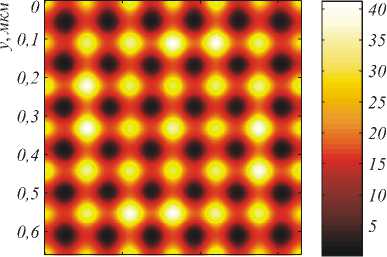
На рис. 3 показаны распределения величины m (а) и интенсивности электрического поля I (б) в подложке на границе раздела волноводный слой/подложка (при z = 0) на одном периоде дифракционной решётки, нормированные на значения без дифракционной структуры. Согласно рис. 3, использование предложенной дифракционной структуры позволяет достичь локального усиления интенсивности электрического поля и величины ОЭФ на порядок в областях с размером порядка 100 нм (период распределений на рис. 3 составляет d/6 = 110 нм ), при этом вид распределений хорошо совпадает с теоретическими оценками (5), (6).

,       0         0,2        0.4        0,6

а)

0,6

.V, МК.М

Рис. 3. Распределения величины m (а) и интенсивности электрического поля I (б) в подложке на границе раздела волноводный слой/подложка на одном периоде дифракционной решётки, нормированные на значения без дифракционной структуры. Параметры структуры: w = 413 нм, h gr = 153 нм , h l = 963 нм . При указанных параметрах дифракционными порядками с номерами (±3, 0), (0, ±3) в структуре возбуждаются квазиволноводные моды TE-типа. Отверстие решётки находится в середине периода

Заключение

В работе исследовано распределение ближнего поля диэлектрических дифракционных структур, состоящих из дифракционной решётки с двумерной периодичностью и однородного волноводного слоя. Показано, что обратный эффект Фарадея в таких структурах локально усиливается на порядок в областях с характерными размерами порядка 100 нм при длине волны падающего излучения 441,6 нм. При этом интенсивность электрического поля также локально усиливается и максимумы интенсивности электрического поля совпадают с максимумами индуцированного магнитного поля. Вид распределений совпадает с полученными теоретическими оценками.

Усиление ОЭФ и интенсивности электрического поля приводит к усилению взаимодействия света с веществом, таким образом, возможно локальное перемагничивание вещества при освещении рассматриваемых структур светом с круговой поляризацией. Последний факт важен для потенциальных применений исследуемого эффекта в устройствах быстрой магнитной записи информации с высокой плотностью. Потенциальные применения рассмотренных структур также включают устройства контроля интенсивности электромагнитного поля и, в частности, оптический транзистор.

Работа выполнена при поддержке государственных контрактов 07.514.11.4060, 07.514.11.4055, 16.740.11.0577, грантов РФФИ 11-07-12036, 10-0201391, 10-07-00553, 11-07-00153 и грантов Президента РФ НШ-7414.2010.9, MK-3123.2011.2.