Усилие при существенно несимметричной прокатке листов

В практике листопрокатного производства достаточно часто имеют место процессы прокатки с несимметрией контактных условий на противоположных контактных поверхностях очага деформации. В ряде случаев это происходит из-за неправильной настройки прокатного стана, неточностей в изготовлении оборудования и т. п., а в ряде случаев создается целенаправленно. При этом достаточно часто одновременно реализуется несколько видов несимметрии. Характерным примером таких процессов является прокатка на стане трио-Лаута, когда имеет место два вида геометрической несимметрии (разные диаметры валков и задача полосы под углом при прокатке в верхнем горизонте), кинематическая несимметрия (один валок приводной, другой неприводной) и трибологическая несимметрия (разные коэффициенты трения из-за разного материала валков). Процессы, при которых одновременно реализуется более двух видов несимметрии, предлагается называть существенно несимметричными.

В настоящее время известно достаточно много работ [1, 2, 3 и др.], посвященных теоретическому анализу процесса несимметричной прокатки. Некоторые из них касаются только одного вида несимметрии процесса, в других одновременно рассматривается несколько видов несимметрии, однако комплексный подход одновременно учитывающий все возможные виды несимметрии отсутствует.

С целью дальнейшего развития теоретических представлений рассмотрим процесс прокатки в валках разного диаметра, изготовленных из разного материала, один из которых приводной, а другой неприводной. Задача полосы осуществляется под углом к оси прокатки. Форма продольного сечения очага деформации для рассматриваемого случая показана на рис. 1.

Основными геометрическими параметрами такого очага деформации являются угол захвата на верхнем валке а_Ов, угол захвата на нижнем валке сг_Он, длина контактной поверхности на верхнем валке Z_B, длина контактной поверхности на нижнем валке /_н, текущая высота очага деформации h . Для определения этих параметров получены следующие соотношения:

]^cosO-Ky ,

°В V ’

_ , Г ho а0н ~ «Ов>

( Rg sm 6 J

^в ^в^Ов ’

41 = ^н^Он >

7    7    1          + 1 )

h = h+—R_ —-- cr , 1* z- где /% и hx - соответственно начальная и конечная толщина полосы; 0 - угол входа полосы в очаг деформации; Rg - радиус верхнего валка; ^=7^/7^ - коэффициент геометрической несимметрии; а — угловая координата сечения очага деформации.

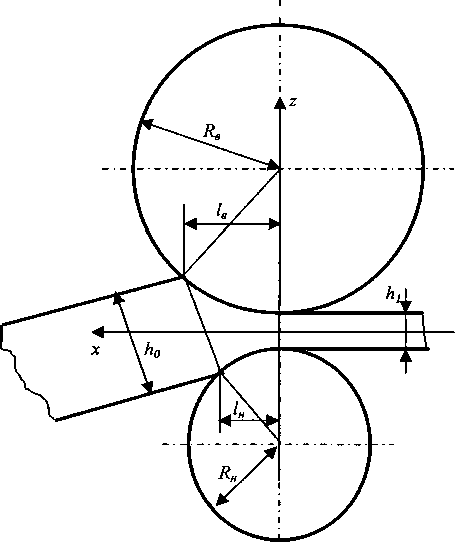
Рис. 1. Форма продольного сечения очага деформации для несимметричного случая прокатки

При прокатке с одним приводным валком ве личину критического угла на неприводном валке можно принять равной 0,5 аОн . Величина критиче ского угла на приводном валке может быть вычислена по формуле, предложенной в работе [4]:

Уп =

/ 1k_R\h arctg —---_?

w+m

+7^arctgO|^         "*Я«0в>

^(1 + ^д) /g^Rg h) J 2

где fg - коэффициент трения на контакте с верх- ним валком; АА = Ay — /г, - абсолютное обжатие полосы.

Определить контактные напряжения в очаге деформации можно с использованием инженерного метода (метода тонких сечений), учитывая геометрические и кинематические особенности рассматриваемого случая прокатки. При этом, в частности, различие в величине критических углов на приводном и неприводном валках приводит к необходимости рассмотрения трех характерных зон по длине очага деформации: отставания, с противонаправленным действием сил трения и опережения. Если принять в качестве закона контактного трения формулу Зибеля, то получим следующие дифференциальные уравнения контактных напряжений [5]: для зоны отставания

^ = [1,15(tga+tg^a) - /в (1 - tgatg^a) -

-/H(l + tg2^a)]^;

для зоны с противонаправленными силами трения ^ = [1,15(tga + tg^a) - /_в (1 - tgatg^a)+ V_H(l + tg²^a)]^;

для зоны опережения

^ = [1,15 (tg« + tg^a) + /в (1 - tgatg^a) + где px - давление на контакте с приводным валком; asc - усредненное по длине очага деформации сопротивление металла полосы пластической деформации; /н - коэффициент трения на контакте с неприводным валком.

Соотношение между давлением р_х на контакте с приводным валком и давлением р_г на контакте с неприводным валком определяется по формуле, полученной из условия равновесия проекций сил на ось, перпендикулярную оси прокатки и пересекающую оси рабочих валков

А = А + ° sc (/в^" - /н^«) , где fB - коэффициент трения на контакте с приводным валком.

В связи с тем, что полученные дифференциальные уравнения при учете всех особенностей существенно несимметричного процесса прокатки не имеют аналитического решения, для выполнения расчетов с их использованием необходимо привлекать численные методы. Одним из наиболее эффективных методов численного решения дифференциальных уравнений является метод конечных элементов (МКЭ). Согласно этому методу очаг деформации разбивался по длине на сим- плекс-элементы, причем разбиение осуществлялось отдельно для зоны отставания, зоны опреже-ния и зоны с противонаправленным действием сил трения. Функции, приближающие искомую функцию рх (а) в пределах конечного элемента с локальным номером (е), в результате локальной аппроксимации записывались в виде р^а) = Р^,+Р^, где N, и Nj - функции формы элемента; Р, и Pj -узловые значения искомой функции.

Локальные номера узлов конечно-элементной сетки / и j отличаются друг от друга на единицу, поэтому их можно связать с локальным номером конечного элемента и функции формы записать в виде

“(е+1)~%)

'  “(е+1)-“(е)’ где а, — угловая координата i -го узла конечноэлементной сетки.

В результате выполненной аппроксимации искомая функция приближенно представлена с точностью до ее узловых значений в виде вектор-„ ,           ~    \ f 0) (2)

нои функции рх (а) = < рх', р\      р\ , где и - число конечных элементов, на которые разбит очаг деформации.

Для определения узловых значений искомой функции был использован метод Бубнова-Галеркина [6], позволивший в конечном итоге свести решение задачи к решению системы п +1 линейных уравнений. Поскольку в рассматриваемой задаче на границах очага деформации отсутствуют продольные натяжения, в качестве граничных условий принято: Р_х = a_sc и Р_п+1 = g_sc .

На основе выведенных формул и выбранных алгоритмов численного решения задачи, к которым относятся алгоритмы метода Бубнова-Галеркина, численного интегрирования и вычисления значений определенных интегралов, составлена программа на языке программирования PASCAL.

Численное моделирование процесса существенно несимметричной прокатки листов с использованием разработанной программы позволило определить ряд закономерностей, присущих этому процессу. Одним из наиболее интересных результатов является зависимость усилия прокатки от соотношения радиусов приводного и неприводного валков (рис. 2). Не трудно заметить, что эта зависимость имеет минимум в диапазоне отношений радиусов приводного и неприводного валков от 1,0 до 1,2. Следует отметить, что этот диапазон

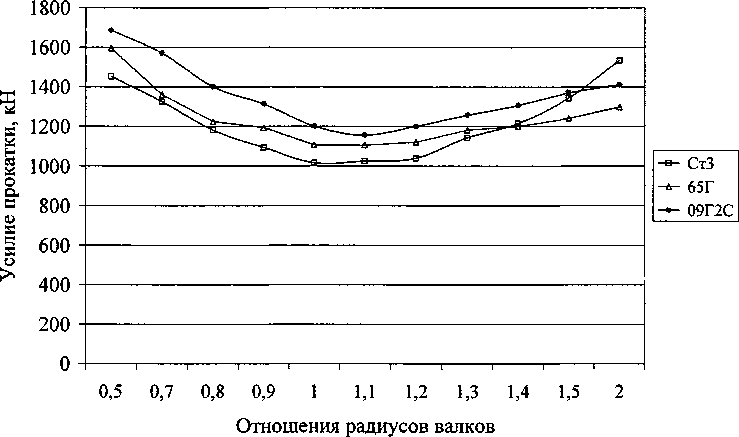
Рис. 2. Влияние отношения радиусов валков на усилие прокатки

о S §

К s'

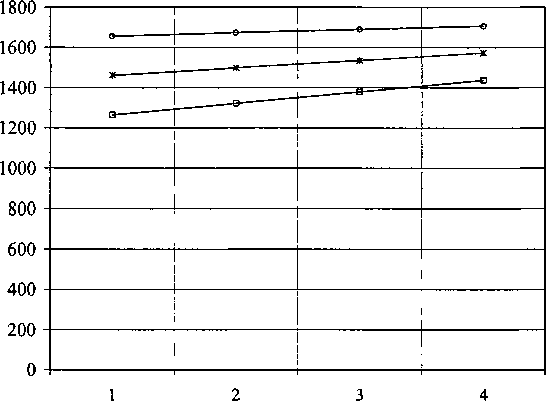
-«- коэф.трения 2,0 коэф.трения 1,5

-о-коэф.трения 1,0

Скорость валков, м/с

Рис. 3. Влияние скорости валков на усилие прокатки

справедлив для различных марок прокатываемых сталей (кривые на рис. 2 соответствуют сталям СтЗ, 65Г и 09Г2С).

Использование разработанной математической модели для инженерных расчетов сопряжено с рядом трудностей. Расчет возможен только с использованием компьютерной техники с установленным на ней программным продуктом, суть которого описана выше. Однако разработанный программный продукт не предназначен для коммерческой реализации и, следовательно, доступен для использования ограниченному кругу специалистов. Создание же собственного программного продукта на основе описанного алгоритма является достаточно сложной и трудоемкой задачей. В связи с этим разработанная математическая модель и созданный на ее основе программный продукт были использованы для проведения вычисли тельного эксперимента и получения на его основе уравнения регрессии, с помощью которого легко выполнить, в частности, анализ влияния различных видов несимметрии на усилие прокатки. При планировании вычислительного эксперимента в качестве факторов выбраны следующие величины:

• -    величина относительного обжатия khlh^ - диапазон изменения 5...40 %;

• -    отношение коэффициентов трения /_в / /_н -диапазон изменения 1.. .2;

• -    температура листа 0 - диапазон изменения 800... 1200 °C;

• -    скорость вращения приводного валка v_B -диапазон изменения 2...5 м/с;

• -    отношение радиусов валков k_R - диапазон изменения 0,5.. .2,0.

В результате получено следующее уравнение регрессии для определения усилия прокатки Р (кН)

Р = 1245,5 - 2456,73— + 472,15 — - 0,720 + ^       /и

+97,82vB +125,82Ь - 40,54vB ^- + 2,580 —.

к ^

Применяя к полученному уравнению необходимое и достаточное условие экстремума получили условия, обеспечивающие экстремальное значение усилия прокатки: 0 = 952°C; v_b=11,6m/c; Ай//^ =0,28; /_в//^=2,4. Исследование полученных экстремальных значений показало, что приведенные значения температуры и относительного обжатия соответствуют минимуму усилия прокатки, а значения скорости валков и отношения коэффициентов трения соответствуют максимуму усилия прокатки. Полученные выводы подтверждаются графиками, приведенными на рис. 3.

Следует отметить, что с использованием разработанной математической модели и составленной на ее основе программы могут быть поставлены другие вычислительные эксперименты и получены уравнения регрессии, связывающие усилие прокатки с другими, влияющими на него факторами. При этом могут быть учтены эффекты взаимо действий факторов более высоких порядков, а также нелинейность зависимости усилия прокатки от влияющих на него факторов. Подобные уравнения регрессии также могут быть использованы для оптимизации процесса существенно несимметричной прокатки толстых листов.