Using FAHP in the educational and vocational guidance
Автор: Essaid EL Haji, Abdellah Azmani, Mohamed El Harzli
Журнал: International Journal of Modern Education and Computer Science @ijmecs
Статья в выпуске: 12 vol.10, 2018 года.
Бесплатный доступ
This paper presents the use of the FAHPmethod (Fuzzy Analytic Hierarchy Process) to help young people choose the most appropriate activity sectors for their profile. This choice is based on three criteria: Professional interests, professional sub-interests and personality traits. This work is a part of a global context aiming to apply the Multi-criteria Decision-Making (MCDM) methods in the vocational guidance according to the process schematized in Figure 3.
FAHP, Multi-criteria Decision making, MCDM Methods, vocational guidance
Короткий адрес: https://sciup.org/15016816
IDR: 15016816 | DOI: 10.5815/ijmecs.2018.12.05
Текст научной статьи Using FAHP in the educational and vocational guidance
Published Online December 2018 in MECS DOI: 10.5815/ijmecs.2018.12.05
The guidance process aggregates several areas of expertise and uses several criteria. Various studies examined the demographic and personal factors, which may influence the choice of professional and educational guidance. Among the personal factors, the level of general ability [1], culture or cultural status [2], values and principles [3], self-esteem [4]self-efficacy, interests [5], personality [6] are decisive factors in the choice of the vocational and educational guidance of pupils. The demographic factors involve the work of the parent [7], the level of study of the parents [8], ethnic origins [2], the socio-economic status, gender, and age of the student [1].
Based on what the researcher said earlier, the use of the MCDM methods is intuitive and applied in the context of various aspects. They are suitable, especially for the choice of a discipline, a profession, a training establishment and a training course.
This article is the logical continuation of the previous article Titled “Using AHP Method For educational and Vocational Guidance” [9], in which we applied the AHP procedure. In fact, the AHP method, despite its good reputation, was the subject of some criticism and extensions. We cite, for example:
-
• in an incomplete hierarchy; more precisely, when all the elements of a level are not connected to all those of the level above the weights obtained do not agree with the intuition which we have of it [10];
-
• several authors question the hierarchical structure itself;
-
• for a large number of alternatives and criteria to compare, there will be an explosion in the number of comparisons in pairs, which makes the method cumbersome and impractical
These difficulties, led to the consideration of the uncertainty and the fuzziness with respect to the expression of the judgments, which led to the fuzzy variant of AHP (FAHP); the opposite of AHP; uses fuzzy numbers with triangular membership functions to represent judgments.
-
II. The FAHP Procedure
-
2.1. Fuzzy set and fuzzy number concepts
The FAHP procedure is widely used by decisionmakers in many problems [11]. It is a MCDM method that combines, both, the AHP procedure and the Fuzzy set concept [12].
Information is the basic building block in any decision-making process. This is true even for the simplest decisions of our daily life such as choosing a meal, choosing a path, and making a trip, etc. However, incomplete or distorted information can be a disruption source of the decision, and it may lead to erroneous decisions. The types of information distortion are diverse: inconsistency, inaccuracy, incompleteness, and uncertainty. In contrast to the human being, the machine based on classical logic cannot be the cause of incomplete or inaccurate data.
Lotfi Zadeh introduced the fuzzy set concept in 1965 to overcome the limitations of classical logic due to vagueness and fuzziness [13]. The fuzzy set concept is widely used in solving many problems in which decisionmakers need to process fuzzy and inaccurate data [14]and.
Formally, a fuzzy subset A of the set x is defined by its membership function^ , defined in the interval [0, 1]:
A = {(x, nA(x))lx e X ЛцА: X ^ [0,1]} (1)
Where /^(x) represents the degree or membership value of an element x to the set A (Kraipeerapun, 2004). So for all x ∈ x:
(1; if and only if x e A p (0 < p < 1); if and only x e (partially) A 0; if and only if x ё A
A fuzzy number M = {(x, цм (x)) | x e X} is a special case of a fuzzy set where the membership function is subject to the following two conditions (Lima Junior, 2014) and (Zimmermann, 2010):
-
• normality: sup^x = 1, V x £ X
-
• convexity:
-
2.2. FAHP analysis steeps
^m(yxi + (1 - 7x2) > min{^M (xi), Цм^)}, V xietx2 £ Aetye [0,1]
There are, however, several types of fuzzy numbers, the most common of which are triangular and trapezoidal fuzzy numbers [15]. In order not to weigh down our manuscript with all of these fuzzy numbers, we will only present the fuzzy numbers we will use in our application.
Consider a triangular fuzzy number M, denoted M = (l, m, u) . Its membership function is defined by:
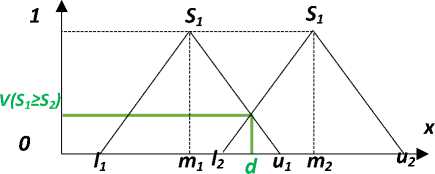
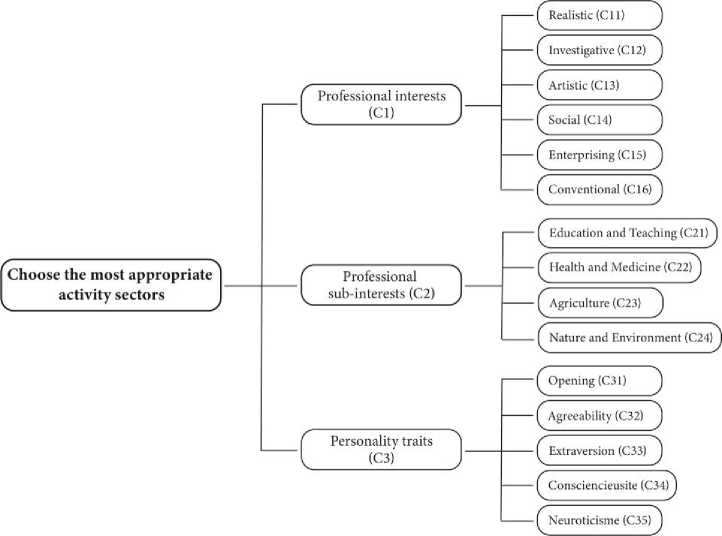
The support of M is the set of elements {xeR /1 A FAHP analysis approach is similar to that of the AHP procedure. First, it is necessary to determine the hierarchical structure of the problem by precisely determining the alternatives, the criteria and their weight, then to construct the corresponding judgment matrix and to make the necessary calculations thereafter. A. Construction of the Judgment Matrix This matrix allows the decision-makers to express the preferences towards the couples of criteria or by reports in under criteria of a criterion. These preferences expressed verbally at the beginning are converted into fuzzy numbers [16] and [17]. For example, Chang uses the conversion scale given in Table 1. Formally, a judgment matrix is defined as follows: A= Mii M2i '" Mi2 ... M22 ■■■ Mim\ M2m ■ = (Mij) i VMni Mn2 ■ Mnm/ avecMij = (lij,m ij,uij) (4) Им(х) = — m-Z m-u 0; - - m—p^ и ;xe [l,u] m-u aiileirs µM(x) Table 1. Fuzzy conversion scale Verbal scale Blurred digital scale Reciprocal fuzzy digital scale Equality perfectly (1, 1, 1) (1, 1, 1) Almost equal importance (1/2, 1, 3/2) (2/3, 1, 2) A little more important (1, 3/2, 2) (1/2, 2/3, 1) Most important (3/2, 2, 5/2) (2/5, 1/2, 2/3) Strongly more important (2, 5/2, 3) (1/3, 2/5, 1/2) Very strongly more important (5/2, 3, 7/2) (2/7, 1/3, 2/5) B. Determination of the values of the fuzzy synthetic intervals The values of the fuzzy synthetic intervals are given by the formula: Fig.1.Triangular fuzzy Number l and u respectively represent the smallest value, the largest support value of M and m the median value of M such that l < m < u. S = Е™^ ^Е^Ет^т^ (5) With Zn=iZi=iMij = (En=i Z^i lij, En=i Ej^i mij, En=i Ej^i Uij) Ej^i Mij = (sr=i lij, Zj™i mij, Sr=iUij) (6) [£?« I”^,,]-1 = 111 (2?=! 27=1 «Ц , 5?=! 27=! ™y , SF=157=1 lt/ C. Calculation of degrees of possibility of superiority The comparison of the valuesS, makes it possible to determine and calculate the degrees of possibility. The calculation of the degree of possibility is given by: V(Si > S2) = I si si ________l2-U1________ . (mi-ui)-(m2-l2); ifmi > m2; ifi2 > ui; if not Fig.2. Intersection between S1 and S2 The degree of possibility for a fuzzy number to be greater than p fuzzy number Ms such that S=1, 2…p is defined by the formula Table 2. Example of the fields of activity 3.1. Choosing a business sector In this step, we propose to a candidate a set of activity sectors and possibly sub-sectors (Education and teaching, Medicine and Health, Nature and Environment, etc.) ranked in descending order of preference based on a set of criteria. Each professional sector may have a set of occupations. The table 2 presents examples of corresponding sectors and trades. V(M > M1,M2,., Mp) = min V(M > Mi) and i = 1,2, .,p D. Weight vector calculation W’ The weight vector W 'of the criteria is given by the formula: W' = (d'(C1),d'(C2)......d'(Cn))T (9) With: C1, C2,....., Cn Are the n criteria. d'(Cj) = minV(5i > 5k) aveci = 1,2, ...,net/c ^ i The vector Normalized weight W is then obtained by the formula: W = (d(Cl),d(C2),..,d(Cn))T (10) 3.2. Choice of a professional activity 3.3. Choice of training 3.4. Choosing a training path The work proposed in this article is part of a more global guidance project consisting of four main phases: choice of sectors of activity, choice of professions, choice of training and choice of training path. This process is shown schematically in Figure 3. Activity area Examples of Jobs Education and teaching Teacher, Pedagogue, Guidance Counselor Health and Medicine doctor, nurse, psychologist, social worker Nature and Environment Environmental Advisor, Gardener, Environmental Protection Engineer, Geologist Agriculture Farmer After choosing a sector of activity, we propose to the candidate a trade or possibly a business capital among sector trades. In this phase, we present a training (possibly a list of training) judged as the best in relation to the chosen profession and other pedagogical and personal criteria. This last step in this process identifies the best possible routes for a candidate considering the three previous steps and other criteria. 4.1. Presentation This study aims to provide a candidate with the sector of activity that suits them the most using the FAHP method. Referring to the process presented in Figure 3, we are in the first step. To do this, we have identified the criteria Professional interests of Holland translated by the RIASEC code, the personality traits according to the BIG 5 model and the professional sub-interests. A. Holland's professional interests Holland (1966) proposed a theory of "professional choice", distinguishing six categories of professional interests (Realist, Investigator, Artist, Social, Entrepreneur, and Conventional), corresponding to different personality profiles. This classification is used to describe people, environments and their interactions; it also serves to establish a typology of "vocational choice" which explains the "professional choice" of an individual. Holland has shown this typology with a hexagonal model defining psychological similarities and interactions between personality types and environments [18, 19, 20]. B. Professional sub-interests Professional interests alone are not enough, in fact a person whose dominant typology is "Realized”, for example, can operate in several areas of professional activities. However, motivation is a primary and determining factor in a practitioner's success and performance. This motivation, sometimes called "taste" is generally referred to in the field of guidance as "Professional Sub-Interests" C. Personality traits 4.2. Structuring the problem A good guidancecannot be conceived without taking into account the "personality" dimension as an important factor, or even extremely important in certain trades. There is currently a multitude of personality analysis methods in the literature review. BIG five is currently considered one of the most popular models of personality analysis [21, 22]. According to this model, five major areas of personality: Neuroticism, Extraversion, Openness, Friendliness, and Consciousness are used to explain individual differences in personality assessments. This evaluation model is nowadays used both for the recruitment question and for vocational training. Figure 4 presents the hierarchical structuring of the criteria and sub-criteria used in this study. Fig.4. Hierarchical structure showing the objective, criteria and sub-criteria of the problem The case study concerns individuals whose: • The RIASEC code is SAICER; • The personality traits according to the method Big 5 are Opening, Agreeability, Extraversion, Consciencieusite and Neuroticisme; • The chosen areas according to the order of its preferences: Education and Teaching (ET), Health Construction of the comparison matrices and determination of the criterion comparison priority vectors and the associated priority vector Table 3 presents the criteria judgment matrix (first level matrix) and Table 4 presents the calculations performed to determine the priority vector. Table 3. Judgment Matrix of Criteria C1 C2 C2 Professional Interests (C1) (1,1,1) (1,-,2) (|,2,1) Professional Sub-Interests (C2) (1.|.1) (1,1,1) (1,3,2) Personality Traits (C3) 2 12 (l,l,l) (^Л) (1,1,1) Table 4. Determination of the priority vector Criteria Fuzzy synthetic interval values (Si) Priority vector Lower (l) middle (m) Upper(u) d' d (normalization) C1 (S1) 0.29 0.46 0.70 1.00 0.56 C2 (S2) 0.21 0.32 0.51 0.62 0.34 C3 (S3) 0.16 0.22 0.34 0.17 0.10 According to the calculations in Table 7, the most important criterion is "Professional interests (C1)" with a weight of 0.56, followed by the criterion "Professional sub-interests (C2)" with a weight of 0.34. 4.3. Summary table of the comparison matrices of the sub-criteria 4.4. Study of alternatives and determination of the best choice To determine the priority vector for the sub-criteria of each criterion, we follow the same approach as that to determine the priority vector of the criteria. Table 5 summarizes the weights of the sub-criteria. Table 5. Local and global weights of the sub-criteria Criterion Professional Interests (C1) Sub-criterion C11 C12 C13 C14 C15 C16 Local weight 0.00 1.8 0.98 1.07 0.17 0.00 Overall weight 0.00 1.01 0.55 0.60 0.10 0.00 Criterion Professional sub-interests (c2) Sub-criterion C21 C22 C23 C24 Local weight 0.83 0.71 0.34 0.00 Overall weight 0.28 0.24 0.12 0.00 Criterion Personality traits (C3) Sub-criterion C31 C32 C33 C34 C35 Local weight 0.83 0.93 0.58 0.00 0.00 Overall weight 0.08 0.10 0.06 0.00 0.00 Table 6. The results of the calculations of comparisons of the alternatives according to the different criteria and sub-criteria Professional Interests (C1) Alternatives C11 C12 C23 C24 C25 C26 X sub-criteria (Overall weight) Goal weight A1 0.00 0.73 0.96 1.02 1.21 1.33 0.00 2.00 A2 0.00 0.88 0.96 1.02 0.72 1.33 1.01 2.10 A3 0.84 0.00 0.00 0.24 1.20 1.33 X 0.55 0.27 A4 0.00 0.75 0.00 0.83 1.20 1.33 0.60 1.38 0.10 0.00 Professional Sub-Interests (C2) C21 C22 C23 C24 X sub-criteria (Overall weight) Goal weight A1 0.81 0.68 0.00 0.00 0.28 0.39 A2 0.68 0.81 0.00 0.00 x 0.24 0.39 A3 0.00 0.00 0.85 0.64 0.12 0.10 A4 0.00 0.00 0.82 0.79 0.00 0.10 Personality traits (C3) C31 C32 C33 c34 C35 X sub-criteria (Overall weight) Goal weight A1 1.20 0.98 0.98 0.45 0.14 0.08 0.25 A2 1.14 0.98 0.98 0.46 0.15 0.10 0.25 A3 1.19 0.00 0.00 0.00 0.00 X 0.06 0.09 A4 0.87 0.00 0.00 0.00 0.00 0.00 0.07 0.00 The results of comparing the alternatives according to the three criteria are shown in Table 7. Table 7. Results of Alternatives Comparison Professional Interests (C1) Professional Sub-Interests (C2) Personality traits (C3) Score A1 2.00 0.39 0.25 2.64 A2 2.10 0.39 0.25 2.73 A3 0.27 0.10 0.09 0.46 A4 1.38 0.10 0.07 1.55 These results show that the best choice is the "Health and Medicine" business line with a score of 2.73, followed by the "Education and Teaching" sector with a slightly lower score (2.64). In this paper, we have presented the use of the FAHP method in the vocational guidance, more specifically in the choice of the sectors of activity most appropriate to the profile of a candidate based on three criteria: Professional interests, sub- professional interests and personality trait. Through this work, we have just shown that the MCDM methods in general and the FAHP method in particular can be of good utility in the field of guidance. However, the use of these methods confronts a certain number of difficulties, the most important of which consist in the construction of the various matrices of the judgment of the criteria and the heaviness of the calculations, considering the large number of comparisons that one must make. [1] S. Davies and N. Guppy, “Fields of study, college selectivity, and student inequalities in higher education” Social Forces, vol. 75, n° %14, p. 1417–1438, 1997. [2] J.C Simpson, “Segregated by subject: racial differences in the factors influencing academic major between European Americans, Asian Americans, and African, Hispanic, and native Americans” Journal of Higher Education, vol. 72, n° %11, p. 63–100, 2001. [3] K.M. Galotti, Making, “A Major real-life decision: college students choosing an academic major”, Journal of Educational Psychology, vol. 91, n° %12, p. 379–387, 1999. [4] Coperthwaite, “The effect of self-esteem, locus of control, and background factors on college students’ choice of an academic major” chez Unpublished doctoral dissertation, The University of Connecticut, Connecticut, USA, 1994. [5] P. J. R. N. E. Betz, “ Current research on parallel measures of interests and confidence for basic dimensions of vocational activity” Journal of Career Assessment, vol. 14, n° %11, p. 56–76, 2006. [6] R. M. S. J. J. L. F. T. L. a. L. W. G. J. W. Lounsbury, “Personality characteristics of business majors as de fined by the Big Five and narrow personality traits” Journal of Education for Business, vol. 84, n° %14, p. 200–206, 2009. [7] K.Leppel, “Race, Hispanic ethnicity, and the future of the college business major in the United Sates” Journal of Education for Business, vol. 76, n° %14, pp. 209–215,, 2001. [8] N. A. S. a. J. L. N. C. Ware, “Undergraduate woman: who chooses a science major?” Journal of Higher Education, vol. 56, n° %11, p. 73–84 , 1985. [9] M. E. E. EL HAJI, “Using AHP method for educational and vocational guidance,” I.J. Information Technology and Computer Science, 2017, vol. 1, pp. 9-17, 2017. [10] R. B. W. B. a. W. T. J. Johnson, “A note on right-left asymmetry in an eigenvector ranking procedure” Journal of Mathematical Psychology, vol. 19, n° %11, pp. 61-64., 1979. [11] L. C. L. Lima Junior, “A comparison between Fuzzy AHP and Fuzzy TOPSIS methods to supplier selection. App” Appl. Soft Comput, vol. 21, p. 194–209, 2014. [12] S. J. R. M. P. Avikal, “A Kano model, AHP and M-TOPSIS method-based technique for disassembly line balancing under fuzzy environment.” Appl. Soft Comput, vol. 25, p. 519–529, 2014. [13] L. Zadeh, “Fuzzy Sets” Information Control, vol. 8, pp. 338-353., 1965. [14] L. L.-J. F. C. L. Osiro, “A fuzzy logic approach to supplier valuation for development.” Int. J. Prod. Econ, vol. 153, p. 95–112, 2014. [15] Q. F. J. Hung, “Prioritizing the Factor Weights Affecting Tourism Performance by FAHP” .Int. J. Eng. Bus. Manag., n° %11, 2013. [16] X. H. Y. D. Y. M. S. Deng, “Supplier selection using AHP methodology extended by D numbers” Expert Syst. Appl , vol. 41, p. 156–167, 2014. [17] W. T. S. D. 2. Jalao,”A stochastic AHP decision making methodology for imprecise preferences” Inf. Sci, vol. 270, p. 192–203, 2014. [18] a. M. L. P. D. Guglielmi, “The Professional Interests According to Holland’s Hexagonal Model Structures and Gender Difference”OSP, vol. 33, n° %13, pp. 409-427, 2004. [19] B. Stevanovic and N. Mosconi, “Les représentations des métiers des adolescent(e-s) scolarisé(e-s) dans l’enseignement secondaire,” Revue française de pédagogie [En ligne], vol. 161, 2007. [20] J. P. R. a. F. H. B. M. Lisa Larson, “Meta-analyses of Big Six Interests and Big Five Personality Factors” Journal of Vocational Behavior, vol. 61, p. 217–239, 2002. [21] L. R. Goldberg, “An alternative description of personality: The Big-Five factor structure” Journal of Personality and Social Psychology, vol. 59, pp. 1216–1229,, 1990. [22] M.Ziegler, “Big Five facets as predictor of job training performance: The role of specific job demands” Learning and individual Differences, vol. 29, pp. 1-7, 2014. [23] H.-J. Zimmermann, “Fuzzy set theory” Wiley Interdiscip. Rev. Comput. Stat., p. 317–332, 2010. [24] M. E. H. Essaid EL HAJI, “Using AHP Method for Educational and Vocational Guidance” nternational Journal of Information Technology and Computer Science (IJITCS), vol. 9, n° %11, pp. 9-17, 2017.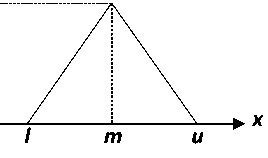
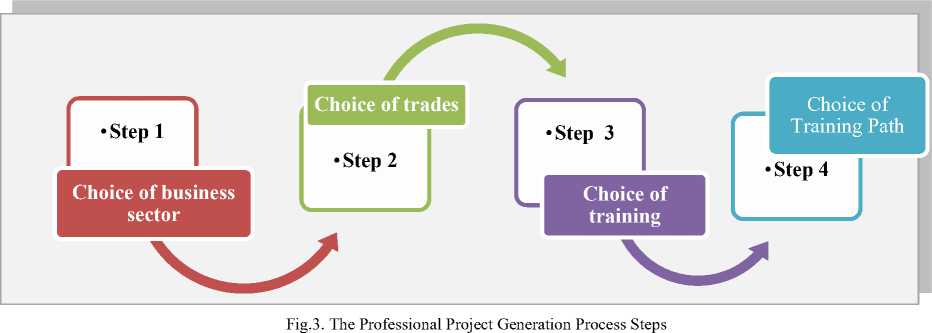
III. A Project of Guidance In Four Phases
IV. Using the FAHP Method to Choose a Better Business Sector
V. Conclusion
Список литературы Using FAHP in the educational and vocational guidance
- S. Davies and N. Guppy, “Fields of study, college selectivity, and student inequalities in higher education” Social Forces, vol. 75, n° %14, p. 1417–1438, 1997.
- J.C Simpson, “Segregated by subject: racial differences in the factors influencing academic major between European Americans, Asian Americans, and African, Hispanic, and native Americans” Journal of Higher Education, vol. 72, n° %11, p. 63–100, 2001.
- K.M. Galotti, Making, “A Major real-life decision: college students choosing an academic major”, Journal of Educational Psychology, vol. 91, n° %12, p. 379–387, 1999.
- Coperthwaite, “The effect of self-esteem, locus of control, and background factors on college students’ choice of an academic major” chez Unpublished doctoral dissertation, The University of Connecticut, Connecticut, USA, 1994.
- P. J. R. N. E. Betz, “ Current research on parallel measures of interests and confidence for basic dimensions of vocational activity” Journal of Career Assessment, vol. 14, n° %11, p. 56–76, 2006.
- R. M. S. J. J. L. F. T. L. a. L. W. G. J. W. Lounsbury, “Personality characteristics of business majors as de fined by the Big Five and narrow personality traits” Journal of Education for Business, vol. 84, n° %14, p. 200–206, 2009.
- K.Leppel, “Race, Hispanic ethnicity, and the future of the college business major in the United Sates” Journal of Education for Business, vol. 76, n° %14, pp. 209–215,, 2001.
- N. A. S. a. J. L. N. C. Ware, “Undergraduate woman: who chooses a science major?” Journal of Higher Education, vol. 56, n° %11, p. 73–84 , 1985.
- M. E. E. EL HAJI, “Using AHP method for educational and vocational guidance,” I.J. Information Technology and Computer Science, 2017, vol. 1, pp. 9-17, 2017.
- R. B. W. B. a. W. T. J. Johnson, “A note on right-left asymmetry in an eigenvector ranking procedure” Journal of Mathematical Psychology, vol. 19, n° %11, pp. 61-64., 1979.
- L. C. L. Lima Junior, “A comparison between Fuzzy AHP and Fuzzy TOPSIS methods to supplier selection. App” Appl. Soft Comput, vol. 21, p. 194–209, 2014.
- S. J. R. M. P. Avikal, “A Kano model, AHP and M-TOPSIS method-based technique for disassembly line balancing under fuzzy environment.” Appl. Soft Comput, vol. 25, p. 519–529, 2014.
- L. Zadeh, “Fuzzy Sets” Information Control, vol. 8, pp. 338-353., 1965.
- L. L.-J. F. C. L. Osiro, “A fuzzy logic approach to supplier valuation for development.” Int. J. Prod. Econ, vol. 153, p. 95–112, 2014.
- Q. F. J. Hung, “Prioritizing the Factor Weights Affecting Tourism Performance by FAHP” .Int. J. Eng. Bus. Manag., n° %11, 2013.
- X. H. Y. D. Y. M. S. Deng, “Supplier selection using AHP methodology extended by D numbers” Expert Syst. Appl , vol. 41, p. 156–167, 2014.
- W. T. S. D. 2. Jalao,”A stochastic AHP decision making methodology for imprecise preferences” Inf. Sci, vol. 270, p. 192–203, 2014.
- a. M. L. P. D. Guglielmi, “The Professional Interests According to Holland’s Hexagonal Model Structures and Gender Difference”OSP, vol. 33, n° %13, pp. 409-427, 2004.
- B. Stevanovic and N. Mosconi, “Les représentations des métiers des adolescent(e-s) scolarisé(e-s) dans l’enseignement secondaire,” Revue française de pédagogie [En ligne], vol. 161, 2007.
- J. P. R. a. F. H. B. M. Lisa Larson, “Meta-analyses of Big Six Interests and Big Five Personality Factors” Journal of Vocational Behavior, vol. 61, p. 217–239, 2002.
- L. R. Goldberg, “An alternative description of personality: The Big-Five factor structure” Journal of Personality and Social Psychology, vol. 59, pp. 1216–1229,, 1990.
- M.Ziegler, “Big Five facets as predictor of job training performance: The role of specific job demands” Learning and individual Differences, vol. 29, pp. 1-7, 2014.
- H.-J. Zimmermann, “Fuzzy set theory” Wiley Interdiscip. Rev. Comput. Stat., p. 317–332, 2010.
- M. E. H. Essaid EL HAJI, “Using AHP Method for Educational and Vocational Guidance” nternational Journal of Information Technology and Computer Science (IJITCS), vol. 9, n° %11, pp. 9-17, 2017.


