Using progressive success probabilities for sound-pruned enumerations in BKZ algorithm

Published Online September 2018 in MECS DOI: 10.5815/ijcnis.2018.09.02

Lattice-based cryptography is one of the main approach in post-quantum cryptography. The breakthrough paper of Ajtai [1], open the way of using Lattices in cryptography. Lattice-based cryptographic primitives designed based on the hard problems in lattices. The shortest vector problem (SVP) and closet vector problem (CVP) are the main basic lattice problems.

Lattice basis reduction is one of the main concepts in lattices which aiming to give a basis with nearly orthogonal vectors. Algorithms for SVP and CVP often use lattice reduction algorithms as a preparation step of solving them. The most well-known and old lattice reduction algorithm for lattice problems is the LLL algorithm, which developed in 1982 by Lenstra (Arjen Klaas), Lenstra (Hendrik Willem), and Lovász [2]. For a lattice with dimension of n, LLL algorithm solves SVP (and most other basic lattice problems) with an approximation factor of 20(n) in polynomial time. In 1987, Schnorr presented BKZ algorithm which leading to somewhat better approximation factors [3]. Schnorr’s algorithm replace the blocks of 2×2 (which be used in

LLL), with blocks of larger size. It is clear that, using larger block size improves the approximation factor, but takes more running time. One the well-known implementation of Schnorr’s algorithm found in Shoup’s NTL library. After public acceptance of Schnorr-Euchner’s BKZ, Chen and Nguyen introduced BKZ 2.0 as the first state-of-the-art implementation of BKZ. BKZ 2.0 algorithm includes new main improvements such as extreme Gama-Nguyen-Regev (GNR) sound pruning [4]. Before development of BKZ 2.0, all security estimates of lattice cryptosystems are based on NTL’s old implementation of Schnorr-Euchner’s BKZ which didn’t include last progresses in lattice enumeration [5]. The security of many lattice-based cryptographic primitives is based on the conjecture which there is no polynomial time algorithm for approximating lattice problems to within polynomial factors [6], therefore lattice basis reduction is one of the main parts of lattice security analysis.

For high dimensional lattices and large block size of BKZ, the running time of BKZ determined by enumerations cost. The improvements introduced in BKZ 2.0 algorithm nearly try to handle enumerations time for sufficiently big block sizes. Other practical technique, which can be considered as a competitor for BKZ 2.0 algorithm, is progressive-BKZ which uses incremental reduction sequences. In this paper we try to tolerate enumerations time in BKZ algorithm by some idea similar to progressive-BKZ [7], while instead of using incremental block sizes, we use incremental success probabilities of bounding function for enumerations of each round. We named this algorithm as BKZ-ProgressPsucc. This technique (BKZ-ProgressPsucc) works based on some claims which we verified them by some experimental results. Also we discussed partially on parallelization and implementation considerations of our contribution.

The remainder of this paper is organized as follows. Section II is dedicated to the sufficient background and review on lattice theory, lattice reduction and main techniques which be used in BKZ 2.0 and progressive-BKZ. In Section III we describe fully philosophy, main idea and the way BKZ-ProgressPsucc works (our contribution in this paper). Section IV dedicated to parallelization consideration in our algorithm. The implementation issues of BKZ-ProgressPsucc discussed in section V. In section VI, we introduced some experimental tests to verify our claims behind the idea of BKZ-ProgressPsucc algorithm. Also some experimental results on implementation of BKZ-ProgressPsucc, showed in section VII (which focused on functionality and performance of this algorithm). Finally, in section VIII, the conclusion of this research be expressed.

• II.    Periliminaries

In this section we try to introduce sufficient background and review on lattice reduction and main techniques which be used in BKZ 2.0 and progressive-BKZ algorithm.

• A.    Lattice Theory

Lattices are discrete subgroups of ^^m and can be defined by a basis. The bases are n-linearly independent vectors b 1 , ..., b_n £ Z^m, which generate a lattice as the set of following vectors:

L(bi..... Ь^^Т^^х^^   (1)

The number of vectors in lattice basis called as rank of the lattice. The volume of a lattice defined as absolute determinant of basis B. Also the length of lattice vectors usually measured by Euclidean norm. We can find many hard problems in lattices, which SVP is a basic of them. For a given lattice basis, SVP defined as the problem of finding shortest nonzero vector in its lattice. In practice, the approximation variant of SVP usually be considered in real applications, which its goal is to find a lattice vector whose length is at most some approximation factor y(n) times the length of the shortest nonzero vector. One of the main SVP solvers is lattice reduction algorithms. Finally we notice to Gaussian Heuristic as one of main observations in lattice theory which defined as follows [5]: “Given a lattice L and a set S, the number of points in S A L is approximately vol(S)/vol(L) ” .

• B.    Lattice Reduction

  As be mentioned, the most well-known lattice reduction algorithm for lattice problems is LLL, which developed in 1982 [2]. LLL reduction is a polynomial time algorithm for approximated SVP (and for most other basic lattice problems) within an approximation factor of 2⁰⁽ⁿ⁾. In 1987, BKZ algorithm proposed by Schnorr as an extension of LLL algorithm. The main idea in BKZ is to replace blocks of 2×2 (which be used in LLL), with blocks of larger size. Increasing the block size improves the approximation factor at the price of more running time. Several variants of Schnorr’s BKZ exist, such as the one be proposed by Gama and Nguyen [8], but all these variants achieve nearly the same exponential approximation factor.

Lattice enumeration algorithms are the main part of block reduction algorithms such as BKZ reduction. For an input lattice block, the enumeration function aims to solve SVP [5]. There are several practical improvements of enumeration algorithm collectively known as Schnorr and Euchner enumeration [9] which including as follows [5]: (a) reducing the search space because of the symmetry of lattices, (b) updating pruning bound in enumeration after finding a shorter vector and (c) enumerating the coefficients of a basis vector in order of the length of the resulting (projected) vector. Schnorr and Euchner proposed enumeration radii of R_k = R * min(1,^(1.05)k/n) as pruning [9], just based on some limited experiments. This pruning was analyzed by Schnorr and Horner [10] in 1995. The analysis of Schnorr and Horner was recently revisited by Gama and et al. [5], who find flaws in it.

• C.    BKZ 2.0 Algorithm

Gama, Nguyen and Regev showed that a well-chosen high probability pruning leads to an asymptotical speedup of 2n/4 over full enumeration [5], then introduced an extreme pruning technique which gives an asymptotical speedup of 2n/2 over full enumeration. Before the introduction of BKZ 2.0, in practice all the security estimates of lattice cryptosystems were based on NTL’s old implementation of BKZ [4]. BKZ 2.0 algorithm was introduced to update last version of BKZ with the latest achievements in lattice reduction and enumeration. Four main improvements were proposed in BKZ 2.0 algorithm, are as follows [4]: early-abortion, sound pruning [5], preprocessing of local bases, and shorter enumeration radius.

The main improvement in BKZ 2.0, is extreme pruned enumeration. Gama, Nguyen and Regev [5] showed that a well-chosen high probability pruning (such as by P succ ^ 95%) introduces the speedup of 2^n/4 over full enumeration [5], but main contribution of them, belongs to extreme pruning technique (such as by p_succ<  0.1%) which gives speedup of (2 — e)^n/2 ® 1.414ⁿ over full enumeration. In fact, sound pruning replaces the inequalities of ||я_к-;+1(и)Н <  R for 1 < l < k — j + 1 by Ня_к-;+1(и)Н < R_; * R where 0 < R 1 < ••• <  R_k- j ₊₁ =1. The vector of (R 1 ,R₂, ... ,R_k- j ₊₁) named as bounding function which can be extreme pruned, or can be not-extreme bounding function. The running time of the sound pruned enumeration is determined by the volume of certain high-dimensional bodies [5]. The extreme pruned enumeration with bounding function Я" uses p —1^ iterations of re-randomization, preprocessing and enumeration samples of the lattice block, where the best solution from all the iterations, considered as the response. The pseudo-code of sound pruned enumeration function introduced in Appendix B from paper [5].

Before each extreme pruned enumeration on the main blocks in BKZ 2.0, we should re-randomize these local blocks, then pre-reduce them. The preprocess reduction and enumeration function offer a trade-off and should be balanced to minimize the overall complexity [11]. The most common approach at the current time is to use block reduction algorithms (such as BKZ) to preprocess the basis before enumerations. Based on the Minkowski’s theorem, one can prove the bounds of Hb1H < Р(п-1)/(/?-1)Л1(В) for first vector of a BKZ p reduced basis [12]. The paper of [12] showed that one can terminate BKZP after a polynomial number of calls to the SVP oracle and provably achieve the bounds only slightly worse than Ц61П < Р(п-1)/(^-1)Л1(В).

The initial enumeration radius R affects the enumeration cost, even though this radius is updated during enumeration [4]. BKZ 2.0 uses Gaussian Heuristic of the lattice blocks with an extra radius parameter of у for determining initial enumeration radii as follows [4]:

mm(^.GH(£[Lk]),\\b^ if k-j> 30 ^ { ||b7?y, other-wise where the Guassian Heuristic GH(£y,k]) defined as 1/(k-j+1)

(Vol(£ [j,k] )/V k-j+i V1)) and in practice, у selected as ТУ = Т1.1.

The early-abort is usual technique in cryptanalysis. This is done in BKZ 2.0 with a parameter which specifying how many SVP oracle should be called. Against other three improvements which try to decrease enumeration cost, this improvement focuses on body of BKZ 2.0 algorithm.

Re-randomization of local blocks can be done simply by pre-computing “random-looking” uni-modular matrices. There are many ways to re-randomize local blocks. The re-randomization strategy in fplll works by permuting basis vectors and triangular transformation matrix with coefficients in {-1,0,1}. Noting that at this time, other algebraic libraries (such as NTL [13]) don’t implement BKZ 2.0 algorithm completely.

• D.    Progressive-BKZ Algorithm

Chen and Nguyen proposed to use progressive-BKZ in preprocess phase of extreme pruning. Progressive-BKZ starting with a small block size and gradually continue with bigger block sizes. For an increasing sequence of {a 1 , .,a_x}, preprocessing will be done in x rounds, so that the reduction in round i is BKZ a [4]. Gama and Nguyen [14] used the sequence of [20,21,22, ...) in their variant of progressive-BKZ, while Haque, Rahman and Pieprzyk [15] used the sequence of [2,4,6, ... ). Chen and Nguyen [4] introduced an automated search algorithm to find optimal choice of a as increasing preprocess block size with step of 10 (see Algorithm 4 in [4]). The optimal increasing sequence in paper [7] generated according to the success probability of bounding functions, enumeration radii and the constant in the geometric series assumption (GSA). Also the paper [7] introduced a simulation for progressive BKZ which is based on idea of Schnorr’s GSA simulator.

• E.    Quality of Basis

The quality of the local basis affect the enumeration cost [4], in which that, by reduction of local basis, the volumes of the local projected lattices £ [ _k- d ₊₁ , _k ] become bigger, and the nodes in most populated depths of enumeration tree be decreased [4]. In practice, the Gram-Schmidt coefficients of random reduced bases produced by some specific reduction notion have a certain “typical shape” [5]. In fact, the absolute slope of logarithmic linear curve of GSO norms Hb * H in a good basis should be low enough [5]. For instance, based on experiments over CJLOSS lattices in [5], it is found slope = -0.085 for LLL reduction and slope = -0.055 for BKZ-20 reduction (in dimension 110) with considering Hb * H² instead of Hb * H.

One of the main asymptotic measures for quality of basis, is q parameter which be defined as Hb * H/Hb * ₊₁H ~ q. This parameter is based on Schnorr’s GSA which says that for a BKZ-reduced basis, we can assume the geometric series of ||b * H = r^1-1 * Hb | H for GSA constant r £ [3/4,1) [7] (while we have q = 1/r). This series is not satisfied exactly in the first and last indexes of basis after some reductions [16], but since it is nearly close to the observations in practice, so we used it in our quality measurements. In fact, we use q factor in this paper for measuring the quality of local block of £ [j, _k ] , by mean measure of (E^k =j ¹Hb i* H/Hb j ₊₁ * H)/(k - j) . Based on d+i GSA assumption for a basis, the relation of 5 (£) = q^ (i.e., 5 ~ ^q) can be used [4]. The other parameter which be used in measuring of basis quality is root Hermite factor¹, which complement q factor in our analysis.

• III. BKZ Algorithm with Progressive Success Probabilities

As be mentioned, our variant of BKZ algorithm uses incremental success probabilities of bounding function for enumerations of each round. Why this algorithm should works truly? What does the idea of incremental success probabilities return to? How can we implement the modification of success probabilities in BKZ algorithm? Are there any other techniques which complementing this idea? In this section, we try to answer these questions fully, in which that, clear main aspects of our contribution.

• A. The Philosophy Behind the Progressive Success Probabilities

The block reduction (such as BKZ) for preprocessing the local blocks, orients these local bases to particular directions. This fact motivates us to declare following claim:

Claim 1. Bettering the reduction shape of a basis more and more, directs this shape to the unique reduction shape of HKZ reduced form of the basis.

¹ Root Hermite factor defined as 5(£) = (—) for basis vol(£)^1/n

В = (b 1 , b₂, ..., b_n) of lattice £ .

A HKZ ² -reduced basis satisfies the condition of ||Ь_г * П = Я 1 (Я [ (Л)) [17]. A HKZ-reduced basis has a unique shape, but it is possible that different set of basis vectors generate this unique shape. Also, bettering the reduction shape is defined by improving the basis quality measurements (such as root-Hermite factor and Q-factor). This claim be verified by Test 1 in section VI.

Our strategy in BKZ-ProgressPsucc doesn’t follow from extreme pruning idea in BKZ 2.0 algorithm. In fact, we use a non-negligible success probability for main enumerations (such as p_succ = 0.1 for block size of 90), so its running time may be intractable for some typical inputs. Noting that success probability of extreme pruning is so much smaller (such as p_succ = 0.001 for block size of 90). To hold these GNR enumerations in a reasonable time bound, some techniques can be introduced as follows (following options have complementary roles in controlling the enumeration time):

• •    Using  a very strong reduction  notions for

preprocessing the local blocks;

• •    Using  a  powerful parallelization for GNR

enumerations;

• •    Using an optimized enumeration radii;

• •    Using the bounding functions which be generated optimally to have least enumerations costs for predetermined success probabilities;

• •    Using a well-defined deterministic aborting condition ³ in body of BKZ-ProgressPsucc, preprocess phase of extreme pruning and GNR enumerations;

The primary method in handling the main enumerations runtime in BKZ-ProgressPsucc is the prereduction of local blocks. We use the concept of success probability in our analysis of BKZ-ProgressPsucc as a relative degree of finding the best vector, not the actual probability of finding the best vector in each enumerations, since following heuristic which be used in estimating success probability of bounding function not to be satisfied when we don’t use uniform rerandomization of local blocks before enumeration [5]:

Distribution of coordinates of target vector v , when written in the normalized Gram-Schmidt basis (6 1* /H6 1* H, ..., 6_n * /H6_n * H) of the input basis, look like a uniformly distributed vector of norm I |v| .

In fact, we use the success probability, only to compare the power of bounding functions in finding solutions, in which that if0p_succ = У can be lead to better solution than the enumeration with p_succ = x. It should be noted that, only if the bounding functions be created in the same family of pruning (such as families of Step bounding function [5],

Piecewise linear bounding function [5], Optimal bounding function [4] and so on), we can compare their costs fairly in the same way. The correctness of our interpretation about the concept of success probability as a relative degree for quality of enumeration solution, or a relative degree for comparing the enumeration cost, be verified by Test 2 in section VI (as the following claim).

Claim 2. An enumeration with higher success probability of a bounding function (and specified family of pruning) on a reduced basis, on average can be lead to better solution vector (with less norm) in more runtime than an enumeration with less success probability of a bounding function from the same family on the same basis.

Since in practice, the bounding functions usually are created to most optimally prune the enumeration trees, so we assume that they are included in family of Optimal bounding function (such as generated by the method introduced in Appendix A from paper [4]).

BKZ-ProgressPsucc and BKZ 2.0, as the same as Schnorr-Euchner’s BKZ, make the reduction shape of basis better after each round, but since BKZ 2.0 used rerandomization on local blocks, so corrupt this shape before each extreme pruned enumerations (see following claims).

Claim 3. An enumeration with initial radii R = ||Й 1* Ц on a basis which be more reduced, on average can be lead to (more and less) better solution vector in less runtime than the same enumeration on the same basis which be less reduced.

Claim 4. On average, after each round of Schnorr-Euchner’s BKZ, the reduction shape of local blocks become better, so (according to Claim 3) the enumeration of them can be lead to nearly better solution vector (when initial radii is R = H& 1* H) in less runtime.

As be mentioned since BKZ-ProgressPsucc don’t rerandomizes the local blocks before each enumeration, it preserves the reduction shape of these local blocks, so the Claim 4 can be applied on the BKZ-ProgressPsucc too. Noting that since in big block sizes, enumerations need to smaller enough initial radii (such as by formula (2a)), so we cannot use Claim 3 and 4 for prediction on goodness of enumeration solution norm, and we just use these claims to discuss on enumeration time.

Similar to progressive BKZ which using decrement of rounds time after each incremental sequence reduction to augment block size, we use decrement of average runtime in enumerations after each round of BKZ-ProgressPsucc to augment the success probability. It should be noted that we cannot use high success probability for main enumerations on the big block size, since the reduction shape of local blocks in first rounds of BKZ-ProgressPsucc is not well enough to lower the cost of enumerations sufficiently. Based on Claims 2, 3 and 4, we should determine the success probability corresponding to desired approximated computation runtime for each main enumeration which should be parallelized on the supercomputers, and augment the success probability of the bounding function after each round to maintain the cost of these enumerations in the desired range of runtime. The increment of success probabilities can be implemented by a sorted array of precomputed bounding functions in a needed range of probabilities (for instance, a sorted array of 1000 bounding functions with optimal cost in the range of 1% < Psucc < 100% with the step of 0.1%). We show an abstract scenario for this idea in the Fig. 1 and Fig. 2, in which that we set psucc = x with average desired runtime (specified by a black dash line in the Fig. 2) for enumeration of local main blocks in the first round of BKZ-ProgressPsucc. After some rounds we observe the decrement of average runtime of enumerations, so we increase the success probability as psucc = y to maintain the cost of enumeration in the desired range (the red arrows in the charts of Fig. 1). In the same way, we increase the success probability as psucc = z and finally psucc = 100% to maintain the cost of enumeration in the desired range (the blue and green arrows in the charts of Fig. 1 and Fig. 2). Noting that, since there is some limitation for an initial radii and reduction shape of lattice blocks, so we cannot expect that, it is essentially possible to reach to sufficiently high success probability for big block sizes.

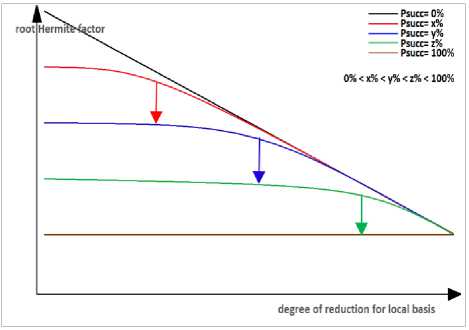
Fig.1. Root Hermite factor of GNR Enumeration on a Wide Range of Reduction Notion up to HKZ Reduced Local Basis.

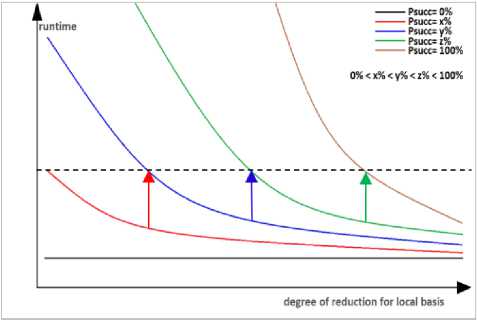
Fig.2. Runtime of GNR Enumeration on a Wide Range of Reduction Notion up to HKZ Reduced Local Basis.

• B.    Modification of Success Probability

The increment of success probability cannot be done simply for high block sizes, since main enumeration time can be intractable for some states, so we should analyze all the states which can be accessed by modification of success probability. At first we should determine a range of acceptable/desired average runtime of enumerations for each round of BKZ-ProgressPsucc based on main block size, the computation power of processing hardware, performance efficiency of parallelizing algorithm, total time limitation of BKZ-ProgressPsucc running and so on. Then we should control the average runtime of main enumerations in BKZ-ProgressPsucc to be included in the determined range (acceptable/desired average runtime of enumerations). We named this range as “Safe desired area”. The probability step is a variable parameter which be used to add with current success probability. The parameter of mamenumP_£ updates (increase/decrease) the probability step mainenumP_step to be adapted with current situation of BKZ-ProgressPsucc rounds. The Fig. 3 shows the state flows of the average enumerations runtime at each round in BKZ-ProgressPsucc which generated by modification of success probability. It should be noted that use of average enumerations runtime as an effective parameter in work flows of BKZ-ProgressPsucc, shows the dependency of this algorithm to computation power of processing hardware and performance ratio of parallelization techniques which be used.

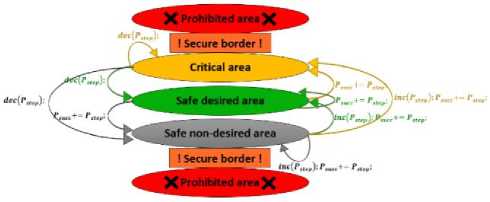
Fig.3. State Flow of Enumeration Time at each Round in BKZ-ProgressPsucc which Generated by Modification of Success Probability

When the average runtime of enumerations in the previous round of BKZ-ProgressPsucc is in the Safe desired area, the success probability psucc should be add with probability step mainenumPstep, then the average runtime of enumerations in current round can be passed in to one of the states of “Safe non-desired area”, Safe desired area and “Critical area”. The Critical area is a range of enumeration times in the rounds of BKZ-ProgressPsucc which be greater than the max bound of Safe desired area, and Safe non-desired area is a range of enumeration times in the rounds of BKZ-ProgressPsucc which be less than the min bound of Safe desired area. When the average runtime of enumerations in the previous round of BKZ-ProgressPsucc is in the Safe nondesired area, the probability step mainenumPstep add with mainenumP£, then success probability psucc should be add with probability step mainenumPstep, and at result, the average runtime of enumerations in current round can be passed in to one of the states of “Safe nondesired area”, Safe desired area and “Critical area”. Based on Claim 4, if the shape of basis in the current round be better very much (in unusual manner), the enumerations of the next round may have too less cost to be parallelized on the processing hardware, so we cannot use the maximum computation power, and at result, it pass into “Prohibited area” (the state at bellow of Fig. 3). In practice by choosing sufficiently small parameter of mainenumPstep and mainenumP£ for big block sizes, BKZ-ProgressPsucc rarely entered into this Prohibited area (the state at bellow of Fig. 3). In fact, BKZ-ProgressPsucc may pass into “Secure border” (a non-negligible part of Safe non-desired area) which still maximum computation power be used but the runtime of enumeration decreased more. When the average runtime of enumerations in the previous round of BKZ-ProgressPsucc is in the Critical area, the probability step mainenumPstep just minus from mainenumP£ , and success probability psucc don’t modified, then the average runtime of enumerations in current round can be passed in to one of the states of “Safe non-desired area”, Safe desired area and “Critical area”. Based on the Claim 4, if the shape of basis in the current round not be better in usual manner, the enumerations of the next round may have so much cost to be parallelized on the processing hardware, so at result, the current state passes into “Prohibited area” (the state at top of Fig. 3) and return the output lattice basis with not acceptable quality (since the predetermined total runtime for BKZ-ProgressPsucc may be spend fully in these enumerations or even enumeration running needed to be aborted). Although we can use the strategy of early-aborting for main enumerations, but in practice, by choosing sufficiently small parameter of the mainenumPstep and mainenumP£ for big block sizes, BKZ-ProgressPsucc rarely entered into this Prohibited area (and in the worst cases, we only passed from Critical area into a Secure border which maximum computation power be used but the runtime of enumerations increased more).

• C.    Pre-reduction for Main Blocks

In addition to bettering the shape of local blocks after each round, BKZ-ProgressPsucc uses a strong preprocess reduction. The success probability of preprocess enumerations (GNR enumerations in preprocess reduction) are considerably more than success probability of main enumerations. The main enumerations with higher block size and less success probability together with the preprocess enumerations with smaller block size and higher success probability, make two complementary roles in reduction of basis. Based on Claim 3, when the initial radii of enumerations in preprocess notion is R = IIM, we declare Claim 5 as follows:

Claim 5. An early-aborted preprocess reduction (when its enumerations used initial radii of R = Нй1*Н and also it can reduce the basis more) on a basis with better shape quality, on average can be lead to better reduction shape in less runtime than the same early-aborted preprocess reduction on the same basis with lower quality.

In fact we use the same strategy as the main enumeration for preprocess, in which that the success probability of preprocess enumerations can be increased after each round. Therefore the local main blocks of first rounds which be less reduced, pre-processed by smaller success probability of enumerations, while the local main blocks of last rounds which be more reduced, preprocessed by higher success probability of enumerations. Since by using preprocess in BKZ-ProgressPsucc, we modify the corresponding local main block, so after each success of preprocess enumeration, we assume that this local main block be succeed (to prevent early full finish of BKZ-ProgressPsucc)!

In this place, we know that BKZ-ProgressPsucc uses three reduction notions at each round: LLL reduction on whole the basis, early-aborted BKZa reduction on each main block (with incremental success probability) and BKZ / on whole the basis (with incremental success probability). It is clear that preprocess reduction in current round (early-aborted BKZa) is namely better than itself in previous rounds (since the success probability of preprocess enumerations in previous rounds is less than or equal to current round one). Although we cannot never assume that the preprocess reduction is stronger (better) than BKZ/? (as be mentioned, they have complementary roles in reduction of basis), but since the success probability of preprocess enumerations is considerably more than success probability of main enumerations at each round, so we hope to make a partially better solutions by combination of them. The strong early-aborted preprocess reduction in BKZ-ProgressPsucc can be configured as low number of preprocess rounds for aborting, together with bigger size of preprocess blocks, sufficiently big success probability for preprocess enumerations and high performance parallelization.

Similar to main enumerations, at first we should determine a range of acceptable/desired average runtime of preprocess reduction for each round of BKZ-ProgressPsucc based on the computation power of processing hardware, performance efficiency of parallelizing algorithm, total time limitation of BKZ-ProgressPsucc running and so on. The parallelization of preprocess enumerations is different from main enumerations, in which that we cannot spend too much time for preprocess enumerations. Then we should control the average runtime of preprocess reduction in BKZ-ProgressPsucc to be included in this determined range which named as Safe desired area. All the concepts which be declared about the Safe non-desired area, Safe desired area, Critical area, Prohibited area and Secure border in main enumerations can be applied fully for runtime of preprocess reduction (not preprocess enumerations). It is clear that these bounds (areas) should be determined independent of choosing the corresponding bounds in main enumeration analysis. Also we should determine the probability step preprocPstep and the step of preprocP£ as the same way declared for main enumerations. The analysis of the preprocess runtime state flow (generated by modification of success probability of preprocess enumerations), fully followed the state flow which be showed in Fig. 3.

Algorithm 1 BKZ-ProgressPsucc algorithm

Start :

^z main = 0 ; ^j main = ^{1 maine} n ^um T_SU m = 0; p ^re p ^rocT sum = 0;

while(z_main< n - 1 && Z_main< n- 1){//while 2 ^k main = minfj main + /? - 1, ⁿ⁾ ;

Z_prep = 0; Restart(abort_prep);

Timer. Start();

^whil e ^(Z prep <  ^k main   J main && dbort prep >  ^0){//wh i ^le 3

^z prep   0 ; ^j prep    ^j main ;

^whil e ^(z pr _e p <  k main - jmain && ^Z prep <  ^k main

//while 4

^k prep = minU prep + a 1, ^k main ) ; ^h = ^min(k prep ⁺ 1, ^k main ) ;

-

7main ){

V ^ ^{ENUM (}jprep , ^k prep ,^ [j_pTep^_prep] ,^ prep , ^p ,Y) ^; if(v * (1,0.....0)) {

Z prep + +; j prep + +; ^lllevd. while 4

abort_prep--; }//end while 3

if(kmain  jmain + 1    P){ preprocN + +; preprocTs^.m+= Timer.TimeSpend();} Timer. Start();

^V ^ ^ENUM ( ^j main , ^k main , ^ {J_ma in ,k_ma in ] , ^ main , P^Y)

if(kmain  jmain + 1

mainenumN + +;

mainenumTs^m+= Timer. TimeSpend();} h = min(kmain + 1, n);

if(v * (1,00)){

LLL(b.....b      ,^^ ^^^tn v,.b,,bf  . .....b ,р,8).

1,    , jmain 1, *-‘i=Jmain 1   1 , jmain*    ,  ^,,

.. at stage jmain"; Zmain = 0; } else £LLL(b!, .,bp,p, 8) at stage h- 1; Zmain + +; } zmain + +; jmain + +; }//end while 2

^if ( ^EE^ ^{е SafeNon} D ^esired A ^rea main) { mainenumP_step+= mainenumP_£;

Output: В

• IV.    Parallelization Consideration

To attack the real-world lattice challenges, the lattice reduction algorithms should be parallelized on the supercomputers. In block reduction algorithms such as BKZ, the main enumerations determine the total runtime of lattice reduction for high dimensional lattice challenges, so parallelizing of main enumerations mostly be noted. Currently, there are various researches which parallelized lattice enumerations as a single running of parallel enumeration [18-21] (which should be considered as a subroutine of lattice reduction algorithms in high dimensional lattices). The parallelization of extreme pruned enumeration consists of so much single threaded enumerations on each randomized BKZ reduced blocks [22], while on other side, the parallelization of nonextreme sound pruned enumeration (and Schnorr’s enumeration) run a single enumeration on many threads.

If we get access to high-speed communicated computer clusters which can dedicate each cluster to a reasonable count of extreme pruned enumeration calls, then it is possible that we can parallelize iterations of each extreme pruned enumeration (including randomization, prereduction and enumeration) too. But we believe that because of efficiency reasons in extreme pruning, users of BKZ 2.0 tend to use more counts of single threaded extreme enumeration calls instead of less counts of parallel ones, since we believe that decrement of the success probability of bounding function together with increment of re-randomized blocks count has better speedup than dedicating more computation power to enumerations with higher success probability in an extreme pruned enumeration running.

The parallelization of extreme pruned enumerations (including so much iterations of randomization, prereduction and enumeration on the corresponding blocks) have least synchronization communications between threads and overlap of steps, so the parallel threads in them namely be independent instances (although the enumeration radius can be shared efficiently between them to be updated by norm of current best vector). Also, since the size of enumeration trees are not necessarily similar for each running of extreme pruned enumeration on randomized blocks, a simple solution for this challenge is to maintain threads busy by generating new instances of extreme pruned enumeration (applying new re-randomization on the local block, then performing preprocess reduction and corresponding enumeration). By using a good parallelizing algorithm and high performance processing hardware, we can reach to efficiency ratio of almost 100% in BKZ 2.0 (one of the researches in this area is [22]). This ratio for non-extreme sound pruned enumeration in proposed parallelization approach is less than 100% (see experimental results achieved in [18-21]). It is clear that BKZ-ProgressPsucc with this parallelization approach can be a best candidate for using the experiences in papers of [18-21], and a motivation to continue this trend in parallelization of lattice enumeration!

• V.    Implementation issues for BKZ-ProgressPsucc

In real world lattice challenges with big average norms of basis vectors, the BKZ algorithm need to manipulate the big (integer/real) numerical values (particularly in calls of LLL function for manipulating very big numbers, and partially in computing GSO coefficients and also squared norm of current projected vector in GNR enumerations which need to sufficient precision of real numbers), so we should choose best implementations of big (integer/real) numbers from different libraries (such as: NTL RR/ZZ, gmp, bigint, boost::multiprecision, MPFR, FLINT, magma and so on). Since NTL library shows the public interests [13], excellence in Software Engineering [13] and good competition with best algebraic libraries [23], so we underlie our implementations of BKZ-ProgressPsucc with this library (NTL) and consequently, we used the data types of RR (arbitrary precision floating point) and ZZ (arbitrary sized integer) for all big (real/integer) numbers. Although the NTL library can be compiled by gmp data types, but since we want to manipulate the functions/structures of NTL in our development, so it is convenient for us to use the data types of RR and ZZ. The experiences show that, basic operations on RR and ZZ, increase the running times with the constant factors over the high performance implementations of big value data types (such as gmp).

It is clear that, for practical applications, the BKZ-ProgressPsucc should be implemented by a faster implementation of big (real/integer) data types (such as gmp) especially in GNR enumeration. In fact, we can implement GNR enumerations in BKZ-ProgressPsucc even by x64 basic data types of double and integer (as the same implementation in paper [5]), but noting that the weak precision of float point (double) can make some partial differences with true work flows of enumeration.

Implementation of LLL function in the BKZ-ProgressPsucc inspired by NTL implementation of LLL and divided into two categories: full LLL (see Algorithm 2) and partial LLL (see Algorithm 3).

Algorithm 2 Full LLL algorithm

• 1:   Input: В = (b1..... b_n) е 2^nxm, GSO Coef Mat ',0

• 2:   for(k = 1 to n){

• 3:     Reduction Step:

for (j = k — 1 to 1) {

• b k ^ b_k- [' kj^1b₇-^;

^for (i = ^{1 to j){} P k,i ^ кд - 1Д к,/ 1д /,« ;}

}

• 4:     Swap Step:

If ((S. II b k—i* II²) >11 ' k,k-i b k-i* + b k* II²) {

• ^b k-1 ^ ^b k ^;k --^; }

else k + +;

• 5:   }//end while

• 6:   Output: B,'

The full LLL reduce whole the basis from the beginning vector to end.

The partial LLL reduce the basis from the startindex (input parameter for start of LLL swap test) to endindex (input parameter for end of LLL reduction), in which that the swap test in the LLL function leads the basis would be LLL reduced from beginning vector (index 0) to endindex. Although the GSO coefficients are the output parameter of NTL LLL, but in our implementation, we use a modified version of ComputeGS function from NTL which computing the needed GSO coefficients (not GSO coefficients of all vectors) [13] before each enumerations.

Algorithm 3 Partial LLL algorithm

• 1:    Input: B' = (bi.....b_endIndex) е T^ndIndexx ™ ,

GSO Coef Mat p.,0 < S < 1, stage startlndex.

• 2:   k = startindex;

• 3:   while (k < endindex){

• 4:     Reduction Step:

for (j = k — 1 to 1) {

bk ^ bk— |Mkj'1b/;

^{for (}     1 ^{to j){} P k,i ^ И кд ^— ^'z, z |/'_; ■ ;;

}

• 5:     Swap Step:

IjT ((S. I b k-1* I²) >I ' k,k-i b k-i* + b k* I²) { ^b k-1 ^ ^b k ^;k --^;} else k + +;

• 6:   }//end while

• 7:    Output: B','

The pseudo-code of GNR non-extreme sound pruned enumeration in Appendix B from paper [5] implemented for BKZ-ProgressPsucc. In enumeration function, we use a bounding function which implemented by a vector of RR data type to prune the enumeration tree. The bounding function vectors in this research computed in the way which inspired by algorithms introduced in Appendix A from paper [4]. After each successes of enumeration function, we don’t abort the enumeration, rather update the best solution and pruning factors (as the same as pseudo code introduced in Appendix B from paper [4]). This enumeration function be called in BKZ-ProgressPsucc for two places: preprocess enumeration (enumeration on preprocess blocks) and main enumeration (enumeration on main blocks). We introduce two different bounding function vectors for each of these enumeration functions (main and preprocess). To avoid generating bounding functions for last main/preprocess blocks of each rounds, we used interpolating the bounding functions as the same as paper [4]. Also our implementation of GNR enumeration uses the optimized version of enumeration radius which be introduced in formula (2a).

The programming language which used for implementation of BKZ-ProgressPsucc is C++. All programming codes of BKZ-ProgressPsucc compiled as 64 bit modules with MSVC compiler for windows platforms. Noting that, we don’t implement parallelization layer for BKZ-ProgressPsucc, so all the tests be run on a single real core.

• VI.    Verification of Claims by Experimental Tests

We discussed five claims which are the basic ideas behind the BKZ-ProgressPsucc algorithm. In this section we show that these claims strongly be verified by experimental tests. Four experimental tests be provided to verify these claims. These experiments were performed on random lattices in the sense of Goldstein and Mayer [24] with numbers of bit length 10n, where n is the lattice dimension. To avoid the intractable running time in our tests, we choose n = 60. We need to randomize these bases in which that not to be oriented in any particular directions. Randomizing a lattice basis can be done by multiplying with uni-modular random matrices. We implement a randomizing function inspired by rerandomize_block(...) function in fplll library [27] with more intensity of randomization, then we check that all the vectors in these random bases have the Euclidean norm which so much far from the Gaussian Heuristic of them. The enumeration radii in the experimental tests of this section use the Euclidean norm of first vector of local block (Hb1*H2)- The code of this four tests compiled with MSVC (x64 bit C++). All the experimental results for running these tests, use the following hardware platform: ASUS motherboard series Z97-K, Intel® Core™ i7-4790K processor (with x64 instruction set, four real cores, processor base frequency of 4 GHz, Haswell microarchitecture), 16GB RAM including two modules of Vengeance®-8GB DDR3 Memory Kit (model of CMZ8GX3M1A1600C9). Noting that, the running times are provided only for a single real core.

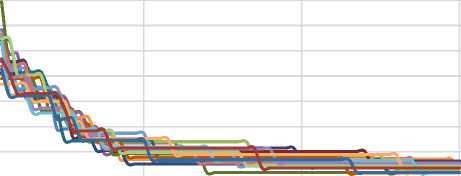
Test 1 : We define a range of reduction degrees for a basis by using the notion of optimal reduction sequence (which be introduced by Chen and Nguyen in paper [4]). Our implementation of optimal reduction sequence run one round of NTL BKZ for each block size of 2 to cb respectively, and we name this implementation as cumulative BKZ^. We can identify the reduction degree of a cumulative BKZ^ reduced basis by its last block size of cb. Here we set the cumulative BKZ^ parameters as 6 = 3/4, prun = 10 and cb = 60. In this test we use a Goldstein and Mayer lattice with seed 0, and compute 20 randomized instances of it. Fig. 4 shows that reduction of all random bases of a lattice directs the bases to unique reduction shape of HKZ reduced form. Moreover, the quality of these 20 randomized bases at the first and end of cumulative BKZ^ reduction of them be showed in Fig. 5 which verify this orientation (to HKZ reduced form) with convergence of these shapes (of random bases) to each other by more reduction (as be discussed, a good basis is one in which the sequence of Gram-Schmidt norms never decays too fast). This test verify the Claim 1.

1.1

1.09

1.08

1.07

1.06

1.05

1.04

1.03

1.02

last block size of cumulative BKZβ

E

1.05

1.045

1.04

1.035

1.03

1.025

1.02

1.015

1.01

1.005

last block size of cumulative BKZβ

Fig.4. On the top, Orientation of 20 Randomized Bases of one Random Lattice to the Shape of HKZ-reduced in the Sense of q -factor, and on the Bellow, Orientation of these Randomized Bases to the Shape of HKZ-Reduced in the sense of root-Hermite factor (each colored line corresponds with a random basis)

20               40               60

block vector index

block vector index

Fig.5. On the top, Quality of a Basis in LLL Reduction, and on the bellow, Quality of the same Basis in Cumulative BKZ/? Reduction with Last Block size of 60 (each colored dotted line corresponds with one random basis)

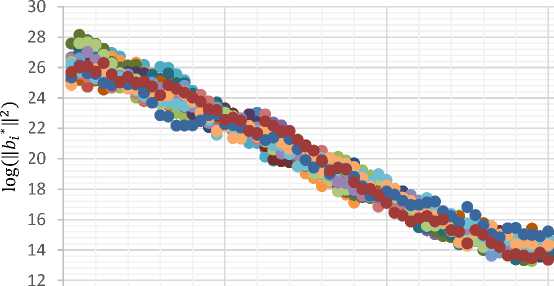
Test 2 : We run our implementation of GNR enumeration [4,5] on the cumulative BKZ / reduction of 20 randomized bases in Test 1. This implementation of GNR enumeration use the float point precision (double data type with size of 8 bytes). Fig. 6 and Fig. 7 respectively show the average root Hermite factor of GNR enumeration solutions and average running time of GNR enumeration in a range of success probability on the cumulative BKZ/? reduced bases in Test 1. It is clear that we can verify the Claims 2 and 3 by results of this test which be shown in Fig. 6 and Fig. 7.

Psucc=1%             Psucc=10%

Psucc=25%            Psucc=50%

Psucc=75%             Exact Solution

Block Size (P)

Fig.6. Average root Hermite Factor of GNR Enumeration Solutions in a Range of Success Probabilities on the Cumulative BKZ ? Reduced form of 20 Randomized Bases

Psucc=1%

Psucc=10%

Psucc=25%

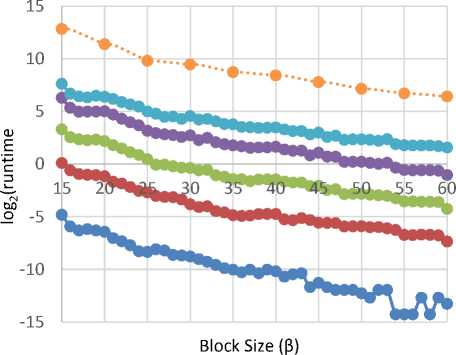
Fig.7. Average Running Time of GNR Enumeration in a Range of

Success Probabilities on Cumulative BKZ/? Reduced form of 20 Randomized bases

We implemented Test 2 with precision of double type (size of 8 byte), and here we try to partially show that, the data type precision has not non-negligible impact on the quality of returned solution of these enumerations. We rerun this test with data types of NTL xdouble and NTL RR for the last cumulative BKZ? reduction (with last block size of 60) on 20 randomized bases. Table 1 verify this fact.

Table 1. Average root Hermite Factor and Runtime (s) of GNR full Enumeration with Different Data type Precision on the Last Cumulative BKZ/? Reduced form of 20 Randomized Bases

real     data     type precision	root-Hermite factor	log 2 (runtime)
Float Point (double)	1.010808038	6.414194742
NTL xdouble data type	1.010808038	9.203115489
NTL RR type data type	1.010808038	13.68060131

—•— BKZp (0=35)  —•— BKZp (в=40)

—•— BKZp (p=45)  —•— BKZp (p=50)

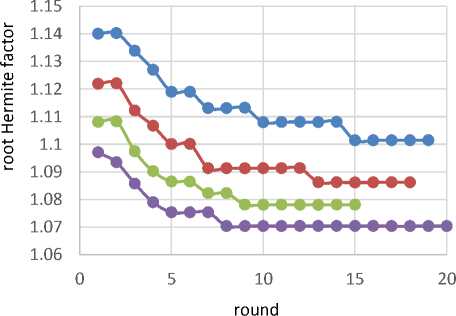
Fig.8. Average root Hermite Factor of Local Bases at each Round of Schnorr-Euchner’s BKZ on Darmstadt Lattice Challenge 500

—•— BKZp (P=35)  —•—BKZp (p=40)

1.017

—•— BKZp (p=45)  —•—BKZp (p=50)

1.016

1.015

1.014

1.013

1.012

1.011

1.01

1.009

1.008

1.007

0         5         10        15        20

round

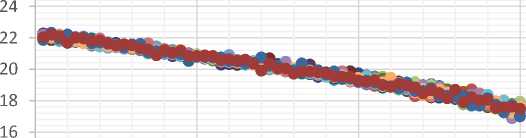
Fig.9. Average q-factor of Local Bases at each Round of Schnorr-Euchner’s BKZ on Darmstadt Lattice Challenge 500

Also it seems that, the data type precision in implementation of computing Gram-Schmidt coefficients lead to some small difference between expected solution of GNR enumeration and practical implementation of it (so it should be investigated in further studies).

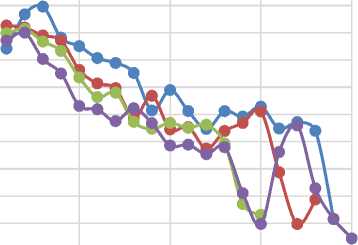
Test 3 : We run NTL BKZ? with block sizes of / = 35, / = 40, / = 45 and / = 50 on the Darmstadt lattice challenge 500 [35,38], and measure the average quality of local bases (q factor & root Hermite factor) at each round (which be shown in Fig. 8 and Fig. 9). Also the Fig. 10 shows the average running time of Schnorr-Euchner-Horner pruned enumerations at each round. It should be noted that this measuring just be applied on the local block with size of / (i.e., we ignore the HKZ-blocks with size of < / in this test). This test verify the Claim 4.

—•— BKZp (p=35)   —•— BKZp (p=40)

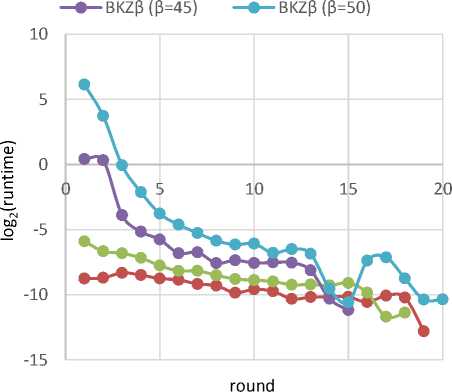
Fig.10. Average Running Time of Enumerations at each Round of

Schnorr-Euchner’s BKZ on Darmstadt Lattice Challenge 500

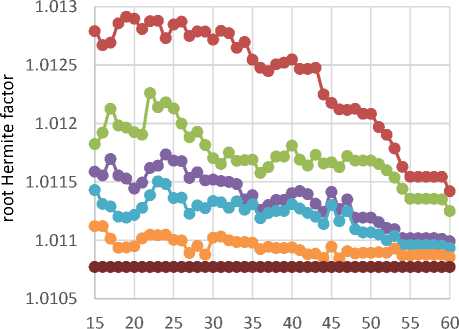
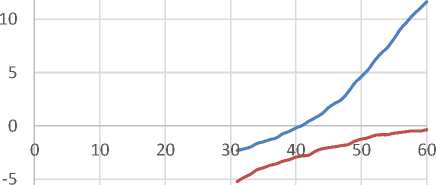
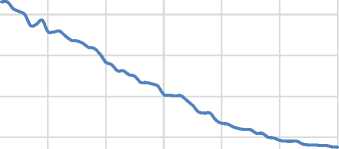
Test 4 : We choose two cumulative BKZ P reduction notions on 20 randomized bases in Test 1, with last block sizes of 10 and 30 (degrees of cumulative BKZP) as two different reduction strength. We run one round of NTL BKZP as the early-aborted BKZP (one round abortion of BKZP be chosen for simplicity) from block size 31 to 60 (as the preprocess reduction stronger than reduction shape of input local bases). The Fig. 11 and Fig. 12 show the average quality of bases after performing one round of BKZP on these two reduction notions (cumulative BKZP with last block sizes of 10 and 30 for 20 randomized bases in Test 1), and Fig. 13 shows the corresponding average running time of one round of BKZP on these 20 randomized bases. This test verify the Claim 5.

aborted BKZβ on comulative BKZ10 reduced basis aborted BKZβ on comulative BKZ30 reduced basis

-10

Block Size (β)

1.024

aborted BKZβ on comulative BKZ10 reduced basis aborted BKZβ on comulative BKZ30 reduced basis

1.022

1.02

1.018

1.016

E

1.014

1.012

0     10    20    30    40    50    60

round

Fig.11. Average root Hermite Factor of Bases after performing one Round of BKZ P on the two Different Cumulative BKZ P Reduction Notions of 20 Randomized Bases

1.055

aborted BKZβ on comulative BKZ10 reduced basis aborted BKZβ on comulative BKZ30 reduced basis

1.05

1.045

1.04

1.035

1.03

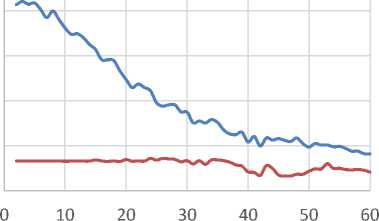
round

Fig.12. Average q-factor of Bases after performing one Round of BKZ P on the two Different Cumulative BKZ P Reduction Notions of 20 Randomized Bases

Fig.13. Average Runtime of one Round of BKZ P on the two Different Cumulative BKZ P Reduction Notions of 20 Randomized Bases

• VII.    Exprimental Results for Implementation of BKZ-ProgressPsucc

Although excessive experimental tests required to have best comparison with other variants of BKZ, but we pass these comparison tests to further studies. In reminder of this section, we just show some results on performance and functionality of our algorithm. In fact, to have better sense on settings of this algorithm, we provided two scenarios of input parameter sets for our tests (which be introduced in the next).

The considerations of software implementation for BKZ-ProgressPsucc be discussed in section V. The experimental tests in this section only use the hard lattice instance of Darmstadt Lattice Challenge 200 [35,38]. The use of lattices with the small dimension (~200), make the opportunity of finishing the BKZ-ProgressPsucc algorithm fully with a sufficiently big main block (such as P = 70) in a reasonable time upper bound, even in presence of not-efficient basic data types! The runtimes of BKZ-ProgressPsucc in all the tests are provided only for a single real core and will be given in the units of seconds. The enumeration radii in these experimental tests uses the Gaussian Heuristic with factor of у = 1.1, also the size of main block is P = 70 and the size of preprocess block is a = 40. The LLL reduction in all of these tests was applied by parameter of 5 ~ 1.

In scenario 1, we use the basic data types of ZZ (for big integer numbers) and RR (for big real numbers). In this scenario, we don’t use the increment of main/preprocess success probability (by zeroing the parameters of mainenumP_ste, p , preprocP_step , mainenumP _£ and preprocP_£ ) which force the BKZ-ProgressPsucc to be fully finished in a reasonable runtime (by lowering the count of rounds). All the instances of BKZ-ProgressPsucc in this scenario fully finished with upper time bound of 500000 s (seconds). The results of experimental tests in this scenario can be seen in Table 2 and 3. In Table 2, the position state which BKZ-

ProgressPsucc be finished, determined by “End State= [Main Round, Main Step, Preprocess Round, Preprocess Step]”. Noting that the main/preprocess steps and rounds start from 0. Also the quality of output basis measured by Hadamard ratio 4 [17] and root-Hermite factor. In fact, here the Hadamard ratio have the role of a simple fingerprint for output basis (besides the role of basis quality measurement).

^ matn. . p succ	Running time	Average time of one round
0.01	15667.4	4491.1
0.02	26579.5	5901.6
0.03	36877.1	8188.0
0.05	74652.4	16575.4
0.065	129866.3	28834.7
0.075	168797.6	37994.0
0.08	188717.2	54096.2
0.09	180782.4	71548.3
0.1	234620.3	92855.8
0.11	418361.3	121789.6

Noting that, since in this scenario, we use RR data type in GNR enumerations, running times in Table 3 increased by a constant factor over the high performance implementations of big value data types (such as gmp or C++ double data type). Also, the low number of rounds in fully finishing of BKZ-ProgressPsucc in these tests caused by: not sufficiently high success probability of main enumerations, using the Gaussian Heuristic as enumeration radii with factor of 1.1, rapidly bettering of the basis shape in BKZ-ProgressPsucc (by pre-reduction of main blocks), and not using the increment of success probabilities.

In scenario 2, we use the basic data types of ZZ (for big integer numbers) and C++ double (for big real of lattice Z.

numbers). Here we use the increment of main/preprocess success probabilities by using the parameter sets which be specified in Table 4.

Table 4. Parameter sets for BKZ-ProgressPsucc in scenario 2

Parameter	Value
p	70
a	40
^■matn * P succ	0.001
R prep . p succ	0.45
mainenumPstep (Initial value)	0.001
preprocPstep (Initial value)	0.05
mainenumP£	0.001
preprocP£	0.05
SafeNonDesiredAreama i n	[0.....0.015)
SafeDesiredAreamatn	[0.015.....0.04)
CriticalAreamatn	[0.04.....0.13)
SafeNonD esiredAreaprep	[0.....0.015)
SafeDesiredAreaprep	[0.015.....0.04)
CriticalAreaprep	[0.04.....0.13)

Since the best trade-off for preprocess time together with subsequent main enumeration time can be observed when these two running times is equal, therefore we use the same time area bound for main enumeration and preprocess in Table 4 (such as S afeDesiredArea ). All the instances of BKZ-ProgressPsucc in this scenario aborted after specified main rounds. Also, the preprocess of main blocks in this scenario used just one round of BKZ₄₀ (corresponds with parameter sets in Table 4). The results of experimental tests in this scenario can be seen in Table 5, 6 and 7.

Table 5. States of BKZ-ProgressPsucc with Parameter sets in scenario 2

Round	^ matn . p succ	^■prep . p succ	mainenumPstep	preprocP step
0	-	-	0.001	0.05
1	0.001	0.45	0	0
2	0.001	0.45	0	0
3	0.001	0.45	0	0
4	0.001	0.5	0	0.05
5	0.001	0.6	0	0.1
6	0.001	0.75	0	0.15
7	0.001	0.95	0	0.2
8	0.001	0.95	0	0.15
9	0.001	0.95	0	0.15
10	0.001	0.95	0	0.15
11	0.002	0.95	0.001	0.15
12	0.004	0.95	0.002	0.15
13	0.007	0.95	0.003	0.15
14	0.011	0.95	0.004	0.15
15	0.011	0.95	0.004	0.15
16	0.011	0.95	0.004	0.15

Table 6. Time results for BKZ-ProgressPsucc with Parameter sets in scenario 2

Round	Round Time	AVG Time of Main Enum.	AVG Time of Prep.
0	-	-	-
1	28.559	0.091	0.126
2	19.027	0.065	0.079
3	11.709	0.041	0.048
4	5.261	0.028	0.011
5	4.664	0.025	0.009
6	3.428	0.015	0.010
7	3.787	0.015	0.013
8	9.878	0.023	0.050
9	4.368	0.015	0.017
10	4.365	0.015	0.017
11	4.314	0.015	0.017
12	3.336	0.007	0.017
13	3.594	0.009	0.017
14	4.06	0.013	0.017
15	4.911	0.019	0.017
16	5.097	0.020	0.018

As be seen in Table 5 and 6, we can control round time of BKZ-ProgressPsucc in our desired running time bound (see Table 4). Unfortunately, since we didn’t use higher success probabilities for main enumerations, the quality of basis in these two scenarios didn’t improve considerably after each round. So, similar to results in Table 2, we can see too smooth improvements of basis quality for scenario 2 in Table 7.

Table 7. Quality of basis after each round of BKZ-ProgressPsucc with Parameter sets in scenario 2

Round	q-factor	root-Hermite factor
0	1.017439181	1.012395383
1	1.016056646	1.011717654
2	1.016134764	1.011717654
3	1.016103012	1.011717654
4	1.01612699	1.011717654
5	1.016116836	1.011717654
6	1.016116836	1.011717654
7	1.016116836	1.011717654
8	1.016116836	1.011717654
9	1.016116836	1.011717654
10	1.016116836	1.011717654
11	1.016116836	1.011717654
12	1.016116836	1.011717654
13	1.016116836	1.011717654
14	1.016116836	1.011717654
15	1.016116836	1.011717654
16	1.016116836	1.011717654

• VIII.    Conclusions

In this research we introduce a new idea for block reduction of bases with high block sizes. BKZ-

ProgressPsucc (our proposed algorithm) is a revised variant of Schnorr-Euchner’s BKZ, which nearly incorporated four improvements of BKZ 2.0 (including: sound pruning, preprocessing of local blocks, shorter enumeration radius and early-abortion) [4]. Since extreme pruning technique not to be used in BKZ-ProgressPsucc, so this algorithm is not a BKZ 2.0 variant. BKZ-ProgressPsucc algorithm is designed based on five claims which be strongly verified in experimental results (as be shown in section VI). These claims declared the basic concepts behind the BKZ-ProgressPsucc algorithm and focus on the primary challenges which our technique faced with. The main idea in this algorithm (BKZ-ProgressPsucc) is that, when the cost of enumerations decreased asymptotically after each round, we can augment the success probability of main/preprocess enumerations in which that, total cost of rounds be maintained in a pre-determined range. It should be noted that use of average enumerations runtime as an effective parameter in work flows of BKZ-ProgressPsucc, shows the dependency of this algorithm to computation power and performance of parallelization techniques which be used. Also we introduce two approaches in parallelizing of extreme and not-extreme pruned enumerations. Table 8 shows a simple comparison between BKZ 2.0 and BKZ-ProgressPsucc.

Table 8. Comparison of BKZ 2.0 Algorithm with BKZ-ProgressPsucc

BKZ 2.0

The power of BKZ 2.0 relies on extreme pruning technique in enumeration of not strong reduced local blocks;

At now, BKZ 2.0 implementation achieved better solutions for real world lattice challenges [4,25];

BKZ-ProgressPsucc

The power of BKZ-ProgressPsucc relies on incremental success probabilities in sound pruned main/preprocess enumeration of strong reduced local blocks;

Currently, we don’t introduced some successfulness of BKZ-ProgressPsucc in practical lattice challenges;

BKZ 2.0 allowed to use nonstrong preprocess reduction on each re-randomized local blocks for an extreme pruning enumeration;	Preprocess notion in BKZ-ProgressPsucc includes: LLL reduction, BKZ a reduction (with incremental success probabilities), BKZ/? reduction (with incremenal success probabilities);
BKZ 2.0 not to be designed with parallelization considerations and also workflow of this algorithm is independent of processing hardware;	Parallelization is a primary concept in design of BKZ-ProgressPsucc which affects the workflow of this algorithm;
By using a high performance parallelization, the efficiency ratio for extreme pruned enumeration reached to 100%;	The efficiency ratio for nonextreme sound pruning enumeration is less than 100%;