Using Wavelet-Based Contourlet Transform Illumination Normalization for Face Recognition

Published Online January 2015 in MECS DOI: 10.5815/ijmecs.2015.01.03

In practice, a face recognition system performs on different conditions of a face image, namely face posture and lighting; however, this paper focuses on illumination conditions only. Our choice is made in consideration of the fact that lighting variations can result in changes in face appearance and that “the variations between the images of the same face due to illumination are almost always larger than image variations due to changes in face identity” [1]. To handle image variations, image representations are commonly used, but they have proven [1] ineffective in dealing with this problem.

To resolve the problem of illumination variations, many approaches, such as the Illumination Cone method of Georghiades et al. [2] and the Quotient Image method of Shashua et al. [3]. Those approaches work on the assumption that faces are aligned. In other words, the images are similar in posture, but different in lighting conditions. To form the three-dimensional shape of an object, there is the shape-from-shading (SFS) approach [4]. This approach works on the image gray-level information and considers either the shape, or the reflectance properties, or the lighting of a face image. The approach using face Eigen-subspace domain by

Belhumeur et al. suggests eliminating some leading principle components which are assumed to get lighting variations only. There exists, however, few methods performing automatic alignment under variable illuminations.

Current alignment methods, such as Active Shape Models (ASM) [6] and Active Appearance Models (AAM) [7], aim at creating models of essential features in a face image, but those models are not reliable enough to be used for searching features as they still suffer the disadvantage of slight variation that might cover delicate features as well as present deceptive features. Using wavelet-based illumination normalization [8] dramatically improves a large spectrum of brightening conditions, so the image edges can be seen. However, the image edges do not have smooth contours and directions.

The coexistence of the face pose and the image illumination variations is the focus of our work. For this problem, pose alignment is not considered as in Illumination Cone method [2]. When pose and illumination variations exist at the same time, contrast enhancement is resulted. Contrast enhancement is usually obtained by utilizing a complete lighting range in a given image. To do it, gray scale transformation is determined, using histogram equalization (HEQ), a practical contrast adjustment method. This method changes pixel values of an image into uniformly-distributed pixel values. However, using histogram equalization just increases the contrast of global images in the spatial domain; it does not bring about a large amount of image details needed for face recognition tasks.

In this paper, the face image illumination normalizing system using wavelet-based contourlet transform is recommended [9]. The recommended system consists of two stages. In stage 1, an image is disintegrated into components of low frequency and high frequency, creating coefficients of various bands, which are later handled individually. Histogram equalization is applied to the approximation of the coefficients of low frequency. In stage 2, coefficients of high frequency are handled with a directional filter bank for smoothing the image edge. The image is normalized thanks to the coefficients modified by an inverse wavelet-based contourlet transform. The normalized image is enhanced its contrast, its edges as well as its details, all of which are necessary to the further face recognition.

The rest of the paper includes these contents: an introduction of the applied wavelet-based contourlet transform in part 2, a detailed description of the recommended approach in part 3 and of the proposed face recognition system with Zernike Moments in part 4, a report and discussion of the experimental results in part 5, and the conclusions in the last part.

• II.    Wavelet-Based Contourlet Transform

WBCT includes two stages. In the first stage, subband decomposition is carried out, which is different from the Laplacian pyramid generated by using only contourlets. In the second stage, angular decomposition is performed with a directional filter bank (DFB), particularly iterated tree-structured filter banks with fan filters [10]. Separable filter banks are used in the first stage and non-separable filter banks, in the second stage. With 2D discrete wavelet transform (DWT), an image is described by the translation and dilation of scaling and wavelet functions. Scaling and wavelet coefficients can be estimated by a 2D filter bank with low-pass and high-pass filters. After one level of 2D decomposition, an image is separated into four sub-bands: LL (Low-Low) produced by approximation coefficients; LH (Low-High), HL (High-Low), and HH (High-High) produced by detail coefficients. At each level ( j ) in the wavelet transform, the traditional three high pass bands matching the LH, HL, and HH bands are acquired, and also DFB with a similar amount of directions is applied to each band. At directions N_D =2 ^L on the finest level of wavelet transform J , the number of directions at every dyadic scale is decreased through the coarser levels (j < J) , resulting in the anisotropy scaling law, width ® length²

In a two-band wavelet transform, signal can be recognized by wavelet and scaling basis functions at various scales.

• f(x) =∑ а , ϕ , (x)+∑∑ ԁ , ψ , (x) (1)

_, are the scaling functions at scale j and _, are the wavelet functions at scale j. _, , _, are scaling coefficients and wavelet coefficients.

Figure 1 demonstrates the diagram of the WBCT with 3 wavelet levels and L = 3 directional levels. Since most of directions are vertical in HL image and are horizontal in LH image, using partly-disintegrated DFB with vertical and horizontal directions in HL and LH bands individually is quite reasonable. However, as wavelet filters cannot split the frequency space into the low-pass and high-pass components perfectly, fully-decomposed DFB needs to be used on each band.

Like the procedure presented in [11], at an l -level DFB there are 2 ^l directional sub-bands with ,0≤ ≤ 2 corresponding synthesis filters and extensive down sampling matrices of ^{( )},0≤ ≤2 defined as:

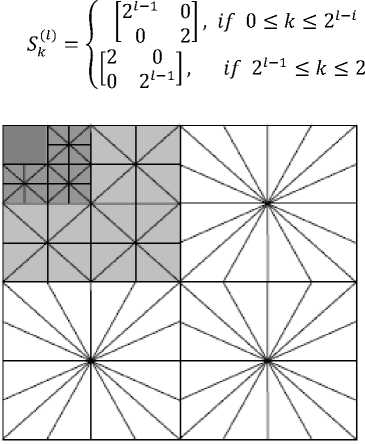
Fig. 1: A scheme of the WBCT with 8 directions at the finest level (ND=8)

Then, { [ - () ]}, 0≤ ≤2, ℤ , is a directional basis for (ℤ); in which ( ) is the impulse response of the synthesis filter ( ). With the normalized divisible wavelet transforms, we obtain a divisible 2-D multi-resolution [7]:

V² = Vj ® Vj ,  and   V²__г = V, ² ® V²

where is the detail space and the perpendicular component of . { _, , _, , _, } _{∈ ℤ} is a normal basis of . If directional level is applied to the detail multi-resolution space , 2 directional subbands of is obtained (Figure 2):

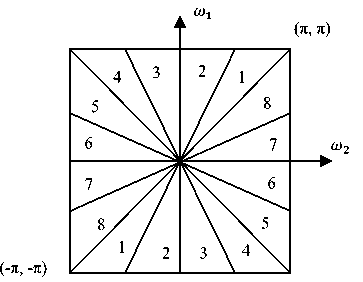
Fig 2: Directional subbands

2 -⨁ k=0

1       ,(  )

,

Defining

^,_,⁽_,⁾ =∑ ∈ ℤ      [   -  ^{( )} ]   _,   ,   =1,2,3,  (3)

w, ^

.

,T] ^^ >^ j’k‘n } nez ² is a basis for the sub-space

• III.    Description Of The Proposed Method

An image is decomposed into both approximation and detail coefficients by wavelet. The image contrast is enhanced by equalizing the histogram of approximation coefficients while the enhancement of image edges is obtained by using a directional filter bank. A given image is normalized by the modified coefficients of inverse wavelet-based contourlet transform. The proposed approach to normalize image lighting conditions is illustrated by Figure 3.

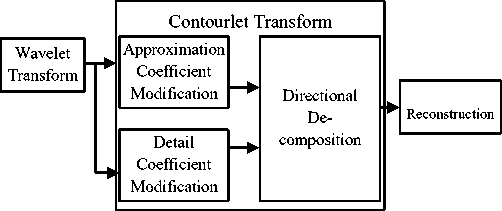
Fig. 3: The chart of the proposed method.

• A.    Histogram Equalization

When both original images and transformed coefficients do not use the whole available dynamic range, the coefficient value range where the histogram equalization is done will be widened for an effective image contrast enhancement.

The image contrast can be enhanced by equalizing the image pixel gray levels in the spatial domain for their ununiform redistribution. Particularly, the histogram equalization organizes the gray levels. A mapping function is implemented on the original gray-level values.

The accumulated density function of the histogram for the processed image is almost equivalent to a straight line. When the uniform distribution is approximated by redistributing pixel brightness, the contrast of the image is enhanced.

Fig. 4: The number of directional subbands in finest wavelet scale

In our paper, the lighting conditions of the approximated image (the LL sub-band in Figure 5) is standardized by using histogram equalization for the contrast enhancement of approximation coefficients.

• B.    Image Contours Sharpening

Obviously, many signal-processing tasks, such as compression, noise reduction, feature extraction and enhancement, take a tremendous advantage of the economical representation of signals available. Contourlet Transform (CT)[12] conceived by Do and Vetterli, one of the recently-developed transforms, aims at increasing the representation scantiness of images over Wavelet Transform (WT). Contourlet transforms are different from wavelet transforms in their feasibility of efficiently handling 2-D unique qualities, i.e. edges, resulted from their two main characteristics: First, it is their directionality, i.e. Contourlet acquires basis functions at different directions in comparison to 3 directions only in the case of wavelets. Second, it is their anisotropy, i.e. the basis functions of contourlet appear at different aspect ratios (according to the scale) while those of wavelets are separable functions, causing their aspect ratio to be equal to 1. CT is considered superior to other geometrically-driven representations, e.g. curvelets [13] in that it is comparatively effective wavelet. Since CT is similar to wavelet transform in structure, a number of image processing tasks performed on wavelets are accommodated to contourlets. Due to the similarities of the WBCT to the contourlet transform, for each LH, HL, and HH subband we can assume the same parent-child relationships as illustrated in Figure 4.

To smooth the image edges and accentuate their directions, 3 wavelet levels and 8 directions at the finest level are used. Noticeably, most coefficients in HL subbands are in vertical sub-bands while those in LH subbands are in horizontal subbands. Figure 5 shows some samples of WBCT coefficients of face images.

Fig. 5: Decomposition of a face image with wavelet-based contourlet

By using wavelet transform, the given image can be separated into frequency components in different bands. With various wavelet filter sets and/or different number of transform levels, different decomposition results can be obtained. A random choice of 1-level db10 wavelets was made for our proposed system. In fact, for the proposed method, any wavelet-filters can be used.

• C.    Image Reconstruction

A normalized image can be restructured from the equalized approximation coefficients and the enlarged detail coefficients generated by the wavelet-based contourlet transform in different directions, as illustrated in Figure.9.

• IV.    Face Recognition System With Zernike Moments

Zernike moments are a series of complex polynomials {V nm (x,y)} that create a complete orthogonal set over the unit disk of x²+y² ≤1 in polar coordinates [14](figure 6). Polynomials are formed as follows

Fig. 6: Example of ZM for feature extraction with face.

Vnm(x,y) = Vnm(r, θ ) = Rnm(r)exp(jm θ )    (4)

In this formula, n is a positive integer or zero; m is integ ers; the subject to constraint n-|m| is even, and |m|≤ n; x=√x² +y² is the length of the vector from the origin to the pixel (x, y); θ = arctan(y/x) is the angle between vector r and x axis in counterclockwise direction; R_nm(r) is Radial polynomial clarified as:

n ₍ )=∑ (  | |)/2

П71771 ( f )=∑s=0

(-1) ()!

^s ![ - |   | "^s_]![    |   | "^s ]!

The two dimensional Zernike moments of order n and with the repetition m for function f(x,y) are as below:

^nm =    ∬ mitdisk (X,У)К∗ (X,У) dxdy)(6)

Where V ^∗ (x,y)=V ,   (x, y).

For the estimation of the Zernike moment of a digital image, modify the integrals using the following function:

2^?i?n =    ∑x∑yf(X,У)К∗ (x,У )(7)

in which x2+y2≤1.

To achieve the scale invariance, each shape is enlarged or reduced in such a way that the image’s 0th regular moment m 00 is equal to the value β set in advance. In the case of a binary image, m 00 matches all the shape pixels in the image. For a scaled image f( α x, α y), regular moments m pq =αp+q+2 m PQ,mpq is the moments of f(x, y).

To make m00 =β , let α=√β/m00 by substituting α = √β/m 00 with m ^′ ₀₀ ; as a result, m00 =α² with m₀₀= β is obtained.

The basic characteristic of Zernike moments is their rotational invariance. If f(x, y) is revolved by an angle α , we will have Zernike moment Z nm of the revolved image defined as

Z =Z e(-jmα)

A face recognition system is a one-to-one matching process in which a person’s identity is matched with an enrolled pattern. Regarding this, our proposed system consists of two main phases: enrollment and verification. In both phases, there are the face image preprocess and the extraction of feature vectors invariant with ZMI feature extraction; however, in the verification phase, there is one more module that is the computation of the matching similarity.

In the enrollment phase, the template images described by ZMI features are classified and then stored in the database. In the verification phase, the input image is first changed into ZMI features and then matched with the claimant’s face image in the database to measure their resemblance. To estimate the resemblance between the two feature vectors, Euclidean distance metric is employed. The obtained distance score is finally compared with a threshold value to determine whether the user should be accepted.

• V.    Experimental Results and Discussion

A. Experimental database

• 1)    Yale Face Database B

  Yale Face Database B [15] produced by Computational Vision and Control Center of Yale University was used to estimate the effectiveness of our proposed illumination nominalization method. This database includes 5760 individual images belonging to 10 persons. Each person has 9 postures and each posture has 64 lighting conditions. Each image is sized 640(w) x 480 (h). Figure 7 displays the sample images of 10 persons from the mentioned database.

Fig. 7: Subjects of the Yale Face Database B.

As dealing with image illumination conditions is the focus of our work, only 64 frontal pose images with 64 lighting conditions from each of 10 persons were chosen for our experiments. Examples of the chosen images are presented in Figure 8.

ИВИН group 5

Fig. 8: 64 lightening conditions of one person’s frontal pose images, extracted from Yale Face Database B

The chosen images are put into 5 groups according to the light-source directions (azimuth and elevation): group 1 (angle < 12 degrees from optical axis), group 2 (20 < angle < 25 degrees), group 3 (35 < angle < 50 degrees), group 4 (60 < angle < 77 degrees), and group 5 (others).

• 2)    Experimental Results

Some significant results have been obtained from the application of wavelet-based contourlet transform on two images from two persons (Figure 9). Particularly, although, the images with equalized histogram are still vague in some way, they become sharper and display more traits. Instinctively, the proposed method can enhance the contrast and sharpen the edges of the images, enabling better face recognition outcomes.

In our experiments, group 1 (7 images for each person) was used as the enrollment database in which each image is matched with each in the other 4 groups for the best match.

(a)                    (b)                   (c)

Fig. 9: (a) Original image; (b) Histogram equalized image; and (c) Enhanced image using proposed method.

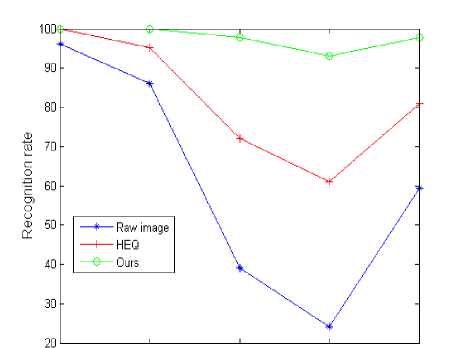
The recognition rates achieved on every single group of images with the use of Euclidean distance nearestneighbor classifier are shown in Table 1 and Figure 10. Obviously, the performance of the proposed method can exceed any other methods that use histogram equalization. Averagely, the recognition rate is improved from 81.03% (achieved by using the HEQ method) up to 97.74%, which is equivalent to 16.71% of improvement in face recognition.

Table 1. Compared recognition rates on Yale Face Database B between the proposed method with that using histogram equalization

Methods	Subset 2	Subset 3	Subset 4	Subset 5	Average
Raw image	96.23	86.15	39.11	24.03	61.38
HEQ	100	95.1	70	59.02	81.03
Our method	100	100	97.82	93.12	97.74

Subset 2 Subset 3 Subset 4 Subset 5 Average

Fig. 10: Compared recognition rates on Yale Face Database B between the proposed method with that using Histogram Equalization

Also, the accuracy rate in verification of the proposed method was compared with that of the wavelet-based and the contourlet-based face recognition systems. ZM with first 10 orders and 36 feature elements were chosen for the experiments. The comparative results in Table 2 and Figure 11 prove that our multimodal system can perform better than other recognition in terms of recognition rate.

Table 2. Compared recognition rates on Yale Face Database B between the proposed method with that using other method

Methods	Subset 2	Subset 3	Subset 4	Subset 5	Average
Waveletbased	97.83	97.35	95.31	92.13	95.66
Contourlet-based	98.2	97.8	95.93	92.5	96.11
Our method	100	100	97.82	93.12	97.74

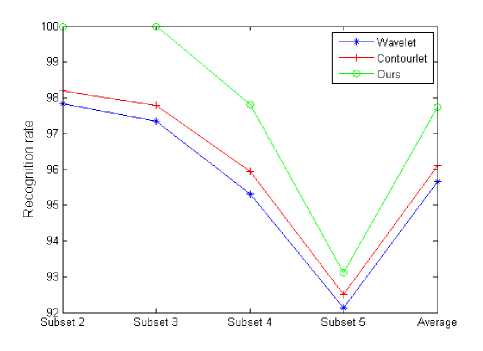
Fig. 11: Compared recognition rates on Yale Face Database B between the proposed method with other methods

• B.    Discussion

From the experimental results, some significant features of the proposed system using wavelet-based contourlet transform normalization (WBCT), ZM descriptor can be seen as below.

WBCT has many properties and among them the most important ones are the following:

• ❖    Wavelet transform can represent face images with smooth areas separated by edges, and it is also powerful in a number of signal and image processing applications, such as compression, noise removal, image edge enhancement, and feature extraction.

• ❖    Contourlet transform is efficient in reconstructing images. Particularly, it can smoothen the contours and sharpen the textures of an image.

• ❖    Histogram equalization can result in effective image contrast enhancement.

• ❖    WBCT combined with HE brings about better face recognition results.

ZM algorithm brings us these benefits:

• ❖    ZM algorithm enables a face-fingerprint recognition system to work on images of various

shapes as its performance is based on the identified center of the image. Also, this algorithm can provide feature sets with similar coefficients for easy computation.

• ❖    ZM is invariant to rotation, scale and translation.

• VI. Conclusion

Currently, wavelet-based methods have been used widely in many face recognition algorithms. In our paper, wavelet-based contourlet normalization is presented as a method specially used to normalize the illumination variations of face images before recognition. In comparison to the methods using histogram equalization, the proposed method has shown to be more advantageous in that it enables a simultaneous enhancement of both the contrast and the edge of an image. Thus, it can facilitate face recognition tasks, particularly in the extraction of features and the recognition steps. Moreover, our face recognition system using wavelet- based contourlet normalization can work more efficiently in a diversified amount of lightening conditions, which is demonstrated by the improvement in the recognition rate achieved from the experiments.