Ускорение факторизации в методе Ферма

Алгоритм факторизации был получен П. Ферма в 1643 г. Основная его идея состоит в том, что составное число С является разностью квадратов, то есть C = p ∙ q = a ² – b ² = ( a – b )( a – b ),

p + q p - q где a = -—-; b = .

Поэтому значение a находится последовательным перебором чисел из множества { E (V C ) + 1, E (V C ) + 2, E (V C ) + 3,... } ⁴ до тех пор, пока не встретится такое a , что значение a ² – C будет являться точным квадратом, то есть b ².

Метод Ферма относится к способу факторизации с экспоненциальной сложностью. Р. Леман усовершенствовал алгоритм факторизации Ферма таким образом, что в худшем случае для его вы- полнения требуется о(C3) операций [1].

В 1982 году Х. Уильямс предложил метод факторизации с помощью последовательностей чисел Люка. В том же году Д. Поллард предложил свой метод факторизации с о(B log B log2 N) действий (B – максимальный простой делитель). В те же годы А. Ленстра предложил метод факториза- ции с помощью эллиптических кривых, появились и другие подходы [2].

В связи со сказанным, сложность проблемы факторизации до некоторого времени делала алгоритм шифрования RSA, основанный на произведении двух простых чисел, весьма надежным. Однако после успешного окончания ряда проектов по взлому RSA стало ясно, что разложение на множители не является невыполнимой задачей, и взлом очередного ключа большей длины – вопрос времени.

Таким образом, создание и разработка новых методов факторизации требует пристального внимания тех, кто использует RSA, так как именно этот алгоритм является самым распространенным способом шифрования, используется во множестве отраслей, применяется в защищенных телефонных сетях.

Важно отметить, что знание закона образования простых чисел [3] дает возможность создавать новые методы факторизации, не прибегая к помощи достаточно трудоемких тестов на проверку простоты чисел. Это существенно ускорит разработку новых алгоритмов факторизации.

Именно на знании закона образования простых чисел и основан изложенный в настоящей статье алгоритм факторизации, улучшающий метод Ферма.

Согласно работе [4], в которой описывается закономерность образования простых чисел, множество натуральных чисел образовано единицей, подмножеством из двух простых чисел 1P = {2, 3}, подмножеством простых чисел вида –P{5, 11, 17, …}, полученных путем вычитания единицы от чисел, кратных 6 {6n – 1}, n = 1, 2, 3, …; (назовем их минус-простыми числами –p – МПЧ), подмно- жеством +P простых чисел {7, 13, 19, ...}, образованном при помощи прибавления единицы к числам, кратным 6,{6n - 1}, n = 1, 2, 3, .„; (назовем их плюс-простыми числами +p - ППЧ), подмножествами четных 2C и нечетных чисел 3 С и подмножествами -С и +С составных чисел, также получаемых вычитанием либо прибавлением единицы к числам, кратным 6. По аналогии назовем их минус-составными числами (МСЧ) и плюс-составными числами (ПСЧ).

Числа, к которым может быть эффективно применим метод Ферма, - это элементы множеств МСЧ и ПСЧ . По определению [4], ПСЧ ⁺С может быть получено как произведение двух ППЧ ⁺ C = ⁺ p • ⁺ q , так и двух МПЧ ⁺ C = p • ^- q , а МСЧ ^-С образуется произведением МПЧ на ППЧ ^- C = ^- p • + q = ⁺ p • - q [3].

Новый алгоритм факторизации

Разложение на множители МСЧ

Если имеется МСЧ -C =p • + q = + p • -q, то метод факторизации Ферма можно улучшить не менее чем в 6 раз, руководствуясь следующей процедурой.

• 1.    Вычислить значение g =

  
  

  C + 1

  и, если оно 6

  
  

• 2.    Среди чисел вида:

• 3.    Среди чисел вида:

четно, перейти к указанию 2, а если нечетно, то -к указанию 3.

E ( -^C ) + 1, E ( >R ) + 2, E (/ C ) + 3,... исследовать на полный квадрат только числа, делящиеся нацело на 6.

E ( ^C ) + 1, E ( J^C ) + 2, E ( J^C ) + 3,... исследовать на полный квадрат только числа, имеющие в остатке 3 при делении на 6.

В общем виде это утверждение выглядит так:

Утверждение 1. Если составное число - число вида -C =p • + q = + p • -q, то среднее арифме-+p+ - q                     с тическое a = —-— нацело делится на 6 при четном значении g или имеет в о статке 3 при нечетном значении g.

Доказательство

Для произведения ППЧ и МПЧ, например при ⁺ p = 6 x + 1, - q = 6 y - 1, где x , y - натуральные, а и g примут вид:

• ⁺ p +^- q 6 x + 1 + 6 y - 1

a = —---- =----------= 3 x + 3 y;

• 2           2

(6 x + 1)(6 y - 1) + 1 _r

g _ у--------L = 6 xy - x + y.

В зависимости от значений x и y возможны следующие случаи:

• 1)    x и y - четные числа: x = 2 m и y = 2 n , имеем: a = 3 x + 3 y = 6 m + 6 n , следовательно, a делится на 6 нацело; а число g = 6 • 2 m • 2 n - 2 m + 2 n = = 2(12 mn - m + n ) - четное;

• 2)    x и y - нечетные числа вида x = 2 m - 1 и y = 2 n - 1, a = 3 x + 3 y = 3 • (2 m - 1) + 3 • (2 n - 1) = = 6( m + n - 1), то есть а нацело делится на 6 .

Так как g = 6 • (2 m - 1)(2 n - 1) - 2 m + 1 + 2 n -- 1 = 2(12 mn - 7 m - 5 n + 3), то оно, так же как и в случае 1, четное;

• 3)    х - четное, а y - нечетное (или наоборот, что равносильно) числа вида x = 2 m и y = 2 n - 1, тогда a = 3 • 2 m + 3 • (2 n - 1) = 6 m + 6 n - 3 имеет при делении на 6 в остатке 3, g = 6 • 2 m (2 n - 1) - 2 m + + 2 n - 1 = 24 mn - 14 m + 2 n - 1.

Пример 1

Рассмотрим составное число С = 70098131. Выяснить, составное оно или простое, можно легко с помощью линейного генератора простых чисел подряд [5].

Поскольку g = 11683022 - число целое и четное, значит, исходя из выше приведенного доказательства, C является МСЧ.

Согласно доказанному выше алгоритму, если число g - четное, то на полный квадрат необходимо исследовать только числа, делящиеся нацело на 6.

Найдем значения a вида:

E ( ^FC ) + 1, E ( ^FC ) + 2, E ( 4^C ) + 3,...:

E (V^ C ) = 8372.

Множество значений a равно множеству {8373, 8374, 8375, _}.

По полученным значениям составим таблицу 1.

Таблица 1

a	8 373	8 374	8 375	8 376	8 377	8 378	8 379
a 2 - - C	8 998	25 745	42 494	59 245	75 998	92 753	109 510
a	8 380	8 381	8 382	8 383	8 384	8 385	8 386
a 2 - - C	126 269	143 030	159 793	176 558	193 325	210 094	226 865
a	8 387	8 388	8 389		8 464	8 465	8 466
a 2 - - C	243 638	260 413	277 190		1 541 165	1 558 094	1 575 025

Остатки от деления значений a на 6 имеют вид:

8373 ≡ 3 (mod 6)

8374 ≡ 4 (mod 6)

8375 ≡ 5 (mod 6)

8376 ≡ 0 (mod 6)

8466…≡ 0 (mod 6)

Среди всех значений a ² – ^– C полным квадратом является число 1575025, то есть b = V a ² - - C = = V8466 2 - 70098131 = 1255.

Таблица 2

a				8 376
a 2 – – C				59 245
a			8 382
a 2 – – C			159 793
a		8 388					8 466
a 2 – – C		260 413					1 575 025

Вывод: решая задачу факторизации методом Ферма, необходимо вычислить 93 значения a2 – –C и проверить, является ли каждое из них полным квадратом. Используя предложенное улучшение метода, достаточно вычислить и проверить лишь 15 значений a2 – –C.

Пример 2

Для разложения на простые сомножители МСЧ –С = 58420049 методом Ферма, необходимо вычислить 213 значений a2 – –C и проверить, является ли каждое из них полным квадратом. Исполь- зуя предложенное улучшение метода, достаточно вычислить и проверить лишь 35 значений a2 – –C.

Разложение на множители ПСЧ

В случае если раскладывать на множители методом Ферма составное число вида +С, возможных остатков от деления a на 6 будет больше. Это связано с тем, что оно может быть образовано двумя способами: + C =p •-q и + C =+ p •' q. В таком случае улучшить скорость работы факториза- ции Ферма можно в 3 раза. Соответствующее описание алгоритма выглядит следующим образом.

~ p + " q 2

Теперь, зная a и b , определим сомножители составного числа ^– С , простоту которых можно проверить при помощи линейного генератора простых чисел подряд [5]:

p = 8466 – 1255 = 7211; q = 8466 + 1255 = 9721.

Таким образом, ^– С = 7211∙9721.

Зная, что полный квадрат находится среди чисел, кратных 6, не надо высчитывать подряд все значения a ² – ^– C.

Предложенный в настоящей работе алгоритм позволяет сократить таблицу 1 до таблицы 2.

для нахождения значения, являющегося полным квадратом, необходимо рассматривать только числа, имеющие при делении на 6 в остатке 2 или 4.

Утверждение 2. Если ⁺ C = p • ~q , то остаток от деления среднего арифметического a = p + q на 6 равен 5 при четном значении f и 2 при нечетном f .

Доказательство

Для произведения МПЧ на МПЧ -p = 6x -1 и q = 6y -1, где x, y - натуральные,

~ p + -q a =------

⁶ x - ¹ + ⁶ y - ¹ = 3 x + 3 y -1; J =

• = 6 xy – x – y .

В зависимости от значений x и y возможны следующие случаи:

• 1)    x и y – четные числа: x = 2 m , y = 2 n , имеем: а = 6 m + 6 n – 1.

Таким образом, остаток от деления a на 6 равен 5. При этом:

f = 6 ∙ 2 m ∙ 2 n – 2 m – 2 n = 2(12 mn – m – n ), то есть f – четное число;

• 2)    когда x и y – нечетные числа вида 2 m – 1 и 2 n – 1, соответственно:

а = 6 m + 6 n – 7, и остаток от деления a на 6 равен 5. При этом:

f = 6(2 m – 1)(2 n – 1) – 2 m + 1 – 2 n + 1 = = 2(12 mn – 7 m – 7 n + 4) – четное число;

• 3)    для сочетания, когда х – четное, а y – нечетное, или наоборот:

а = 6 m + 6 n – 4. При делении a на 6 остаток равен 2. При этом:

f = 6 ∙ 2 m (2 n – 1) – 2 m – 2 n + 1 = 24 mn – 14 m – – 2 n + 1 – нечетное число, так как при делении на 2 имеет в остатке единицу.

Утверждение 3. Если ⁺ C = ⁺ p • ⁺ q , то сред-

.                  +p++q нее арифметическое a = —-— имеет в остат- ке 1 при делении на 6, если значение f четно, или остаток равен 4 при нечетном значении f.

Доказательство утверждения аналогично двум предыдущим.

Пример 3

Для разложения на простые сомножители ПСЧ ⁺ С = 71396707 методом Ферма необходимо вычислить 116 значений a ² – ^– C и проверить, является ли каждое из них полным квадратом. Используя предложенное улучшение метода, достаточно вычислить и проверить лишь 39 значений a ² – ^– C.

Стоит отметить, что в алгоритме RSA простые p и q рекомендуется выбирать таким образом, чтобы задача разложения числа С была достаточно сложна в вычислительном плане. Одним из требований, предъявляемым к используемым в RSA простым числам, является небольшая величина наибольшего общего делителя чисел p – 1 и q – 1; желательно, чтобы НОД( p – 1, q – 1) = 2 [10].

Легко показать, используя закон формирования простых чисел [3], что НОД( p – 1, q – 1) = 2 только в двух случаях: когда p представимо в виде 6 n + 1 и q в виде 6 m – 1 или при p = 6 n – 1 и q = = 6 m – 1, то есть составное число может быть как ПСЧ, так и МСЧ, но ПСЧ в этом случае формируется только как произведение МПЧ на МПЧ.

Таким образом, из рассмотренных выше утверждений практическое приложение для алгоритма факторизации применительно к RSA могут быть только первые два. Их можно объединить в следующую систему указаний:

• 1)    выяснить, элементом какого множества число является С : ПСЧ или МСЧ;

• 2)    если С – МСЧ, нужно воспользоваться утверждением 1 , иначе – утверждением 2 .

Итак, в связи с тем, что в шифровании методом RSA не участвуют одновременно два ППЧ, предложенный в работе алгоритм, применимый к криптосистеме RSA, эффективнее метода факторизации Ферма не менее чем в 6 раз.

Отметим, что при последовательном вычислении скорость работы предложенного алгоритма не может конкурировать со способами факторизации с субэкспоненциальной сложностью. Наиболее эффективным из них на данный момент считается алгоритм решета числового поля, эври- стическая оценка сложности которого составляет 12

e(к+о(DXlogC)3(loglogC)3 арифметических операций при некоторой постоянной k [2].

Построим модель вычислений, чтобы провести анализ и оценить возможность параллелизма улучшенного алгоритма. Модель нашего алгоритма представлена в виде графа «операции – операнд» на рис. 1.

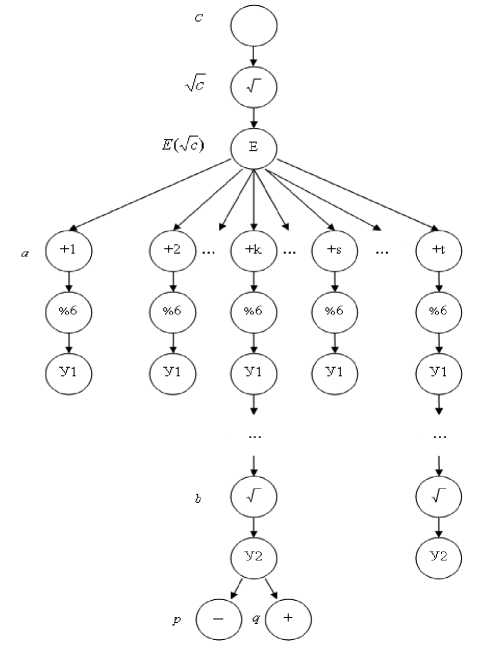
Рис. 1. Модель алгоритма факторизации в виде графа «операции – операнд»

Арифметические операции, записанные в вершинах графа, соответствуют арифметическим операциям языка программирования С .

У1 (условие 1) – равенство остатка от деления на 6 (остаток получен на предыдущем шаге операцией %6) в зависимости от того, каким числом является С : МСЧ или ПСЧ.

У2 (условие 2) - значение V a ² - C должно быть целым.

Очевидно, что в модели (рис. 1) существуют операции, между которыми нет пути, а значит, они могут выполняться параллельно.

Соответственно предложенный нами алгоритм может быть легко распараллелен, что дает возможность существенно увеличить его эффективность по мере подключения вычислительных мощностей при осуществлении факторизации.