Ускорение обучения нейронной сети с отбором обучающих примеров

Начиная со второй половины 80-х годов, теория искусственных нейронных сетей пользуется большой популярностью в области научных исследований, и, судя по публикациям, в различных областях становится обычным исследовательским инструментом. Нейронные сети все чаще применяются для решения разных прикладных задач. Во многом это происходит благодаря большому скачку в развитии вычислительной техники. Так же немаловажную роль играет существование простого алгоритма обучения популярных многослойных нейронных сетей прямого распространения, не требующего предварительного анализа данных и имеющего приемлемую скорость работы – алгоритма обратного распространения ошибки.

Постоянно растущая сложность прикладных задач, нелинейное увеличение объемов данных и их размерности оставляет актуальной задачу повышения эффективности алгоритмов, используемых для обучения нейронных сетей. Основной задачей становится уже не просто обучение, а нахождение нейронной сети, наилучшим образом решающей поставленную прикладную задачу. При этом обучение становится операцией в решении задачи оптимизации структуры сети. В этом случае потребность в быстром обучении еще больше возрастает.

В данной работе рассматривается изменение общего метода обучения нейронной сети по алгоритму обратного распространения ошибки. Нейронная сеть используется для распознавания изображений рукописных цифр. Рассматривается возможность эффективного распараллеливания модифицированного алгоритма обучения.

Исходные данные для обучения нейронной сети

Нейронная сеть предназначена для распознавания изображений рукописных цифр, используемых при написании индекса в зоне кодового штампа почтовых отправлений письменной корреспонденции. Особенностью написания цифр является то, что в кодовом штампе допускается как стилизованное написание цифр в виде определенного набора штрихов, так и обычное написание в виде арабских цифр, что увеличивает разнообразие распознаваемых знаков и затрудняет использование классификаторов, использующих предположения о группировке дан- ных в выпуклых областях. В данном случае чаще используют структурный анализ, скрытые марковские модели, нейронные сети. В случае использования нейронных сетей есть возможность производить распознавание изображений непосредственно как набора чисел – значений интенсивностей пикселов, не производя выбор признакового пространства и отображения в него исходных изображений.

Для распознавания цифр в качестве признаков используются значения интенсивностей пикселов изображения, получаемого из исходного путем следующих преобразований. Во-первых, все изображения вписываются в прямоугольник заданного размера для того, чтобы количество признаков у любого изображения было одинаковым. Во-вторых, нормализуется динамический диапазон значений интенсивностей элементов сжатого изображения. В результате получаются изображения размера 8х6 пикселов, интенсивность которых находится в диапазоне 0,255, причем значение интенсивности самого светлого пиксела – 255, а самого темного – 0. Примеры изображений, распознаваемых нейронной сетью, показаны на рис. 1.

Рис. 1. Изображения, распознаваемые нейронной сетью

С точки зрения задачи обучения можно отметить две особенности. Количество признаков распознаваемых объектов является довольно большим, в нашем случае с учетом унификации параметров нейронов число признаков равно 49. Количество данных для обучения может превосходить на несколько порядков размерность признакового пространства, так как получение различных изображений рукописных цифр не представляет собой большую техническую сложность.

Модифицированный алгоритм обучения

Обучение нейронной сети производится с помощью алгоритма обратного распространения ошибки. Для обучения используются обучающие примеры, представляющие собой пары (X, D). Каждая пара включает в себя вектор известных входных сигналов сети X (признаки изображения) и соответствующий вектор желаемых выходных дан- ных D (значения нейронов выходного слоя сети). Обучение представляет собой минимизацию некоторой оценки работы нейронной сети, зависящей от параметров нейронов и множества обучающих примеров. В качестве оценки обычно используется функция [2-5]

H ( w ) = ¹ Z ( У, q - d i,q ) 2 ,                   (1)

2i,q где yi,q - реальное состояние нейрона i выходного слоя нейронной сети при подаче на ее входы q-го обучающего примера; di,q - требуемое выходное состояние нейрона i выходного слоя нейронной сети при подаче на ее входы q-го обучающего примера; w – вектор настраиваемых параметров нейронной сети. Данная функция, как правило, минимизируется методом градиентного спуска. Описание алгоритма хорошо известно [1-5], поэтому приведем только основные этапы обучения:

• 1.    Инициализация параметров нейронной сети случайными малыми значениями.

• 2.    Предъявление нового входного вектора X и вычисление реального выходного вектора Y (прямой проход).

• 3.    По соответствующему вектору желаемого выходного вектора D и полученному на предыдущем шаге вектору Y корректировка параметров нейронной сети w (обратный проход).

• 4.    Если ошибка сети существенна, переход к шагу 2. Иначе – конец.

Сети на шаге 2 предъявляются все обучающие примеры, чтобы сеть не забывала одни по мере запоминания других. В качестве активационной используется дифференцируемая функция, например, сигмоид с экспонентой f (5) = -1 + 1 .                        (2)

• 2 i + e-к

При распознавании образов нейроны выходного слоя, как правило, соответствуют классам образов (позиционный способ кодирования классов). Для того чтобы интерпретировать результаты работы нейронной сети, часто используют решающее правило «победитель забирает всё», при котором образ считается принадлежащим тому классу, чей нейрон имеет максимальный выход.

По функции (2) видно, что научить сеть в точности воспроизводить желаемый выходной вектор (в данном случае это +0,5 для выхода нейрона, соответствующего классу входного вектора, и –0,5 для выхода остальных нейронов) невозможно из-за того, что желаемые значения являются пределами функции. С учетом необходимости получения от нейронной сети отказов от распознавания или распознавания с некоторой точностью допускается отклонение e выходов нейронной сети от желаемого значения. Правило интерпретации выходов сети принимает следующий вид класс i, если (0.5-yi < e) здесь e – малая положительная величина, y – уровень нейрона выходного слоя.

Опыт показывает, что при большом количестве обучающих примеров минимизация критерия (1) не всегда приводит к получению обученной распознаванию всех заданных примеров нейронной сети, даже если она распознает все тестовые примеры. Объяснить такое явление можно тем, что количество тестовых примеров по сравнению с обучающими мало, а среди обучающей выборки может попасться небольшое число особенных примеров. Если расстояние от таких примеров до ближайших соседей из того же класса в признаковом пространстве не позволяет их обобщить, то нейронная сеть «жертвует» правильной классификацией таких примеров ради уменьшения части суммы, входящей в (1) и соответствующей большому числу обобщенных примеров. В то же время, увеличив допустимый отрыв выходов нейронной сети от желаемых значений по отношению к большинству выходных векторов, можно добиться правильной классификации всех обучающих примеров. При этом минимизируемая оценка (1) значительно увеличится.

Для преодоления описанных сложностей используется несколько другая схема обучения, отличие которой от вышеприведенной заключается в том, что корректировка параметров нейронной сети в пункте 3 происходит только при неправильной классификации или отказе от распознавания. В качестве оценки работы нейронной сети используется количество ошибок на обучающей выборке

E (w, e) = Z I (Dq, Yq), (4) q где q = 0..Q-1 – индекс по обучающим примерам; I – функция ошибки, определяющая несоответствие желаемого выхода нейронной сети D и реального выхода Y для обучающего примера q по правилу (3).

С точки зрения количества ошибок (4) полностью обученная сеть будет удовлетворять равномерной оценке с точностью e :

H ⁽ w ) = ( ^max| d iq ^- y, q | ) <  e . (5) i q

Модифицированный алгоритм обучения использующий процедуру обратного распространения ошибки для обучения нейронной сети позволяет минимизировать равномерную оценку (5) путем использования процедуры. Далее в тексте такой алгоритм обучения будет называться выборочным а первоначальный – исходным.

Результаты экспериментов

Для сравнения характеристик обучения по двум алгоритмам были проведены эксперименты по обучению нейронной сети распознаванию изображений цифр. Характеристики изображений и способ распознавания описаны в пункте 1.

Так как обучение начинается с определения случайных величин в качестве начальных значений параметров, оно носит стохастический характер. Для получения результатов процедура обучения для каждого алгоритма выполнялась 47 раз при различных начальных условиях. Количество обучающих примеров было различным: данные приводятся для обучения 50, 150, 500, 1500 и 5000 изображениям. В силу ограниченности системных ресурсов обучение большему числу изображений для экспериментов не использовалось. На практике в такой ситуации использовалось дообучение по выборочному алгоритму сети, натренированной на небольшом (несколько тысяч) количестве изображений.

Первый эксперимент заключался в сравнении возможности обучения нейронной сети при различных начальных условиях. Если обучение останавливалось на длительный период, то считалось, что сеть не может обучиться. На рис. 2 показана диаграмма частоты полного обучения для обучающих выборок различного объема. Во всех случаях чаще полное обучение происходит при использовании выборочной схемы.

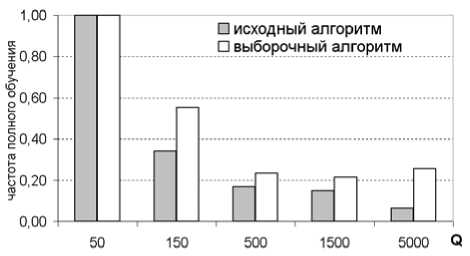
Рис. 2. Частота обучения нейронной сети. Q – количество обучающих примеров

Вторым показателем, по которому сравнивались алгоритмы обучения, было среднее время до полного обучения. Для его расчета использовалось время только при тех начальных условиях, которые заканчивались полным обучением. Результаты приведены на рис. 3 в виде диаграммы для обучающих выборок различного объема. Для времени используется логарифмическая шкала. Во всех случаях полное обучение происходит быстрее при использовании выборочного алгоритма.

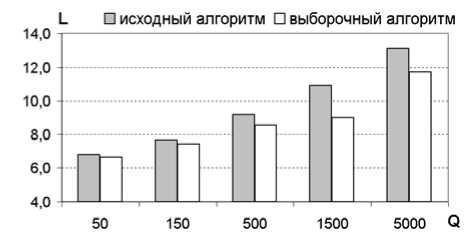
Рис. 3. Среднее время обучения нейронной сети.

Q – количество обучающих примеров; L = log 2 T, где T – время обучения в секундах

Обоснование эффективного распараллеливания алгоритма обучения на кластере

Считается, что нейронные сети обладают большим потенциалом для распараллеливания. Это справедливо для многопроцессорных вычислительных машин с общей памятью. Для высокопроизводительных вычислительных систем, построенных по кластерному типу, дело обстоит по-другому. Большое время доступа к данным, находящимся в распределенной памяти, и операций обмена между процессорами по сравнению со временем вычислений результата работы нейронной сети при использовании локальной памяти приводит к нецелесообразности реализации нейронных сетей на кластерах.

Обучение нейронной сети – процесс более продолжительный по сравнению с её прямым функционированием. Если удастся выделить в алгоритме обучения некоторый большой объем вычислений, при котором не требуется обмена данными, то станет возможным распараллеливание обучения нейронных сетей на недорогих по сравнению с многопроцессорными ЭВМ кластерах.

В данной работе для обучения использовался алгоритм обратного распространения ошибки, который является итеративным. На каждом шаге происходит корректировка параметров нейронной сети и перейти к следующему шагу невозможно, пока не закончится текущий. Корректировка параметров приводит к необходимости обновления данных, а, следовательно, к операциям обмена между задачами параллельного алгоритма (по модели канал/задача [6]). Время, затрачиваемое на обмен, определяется количеством корректировок, т.к. остальные данные (обучающие примеры) во время обучения не меняются и могут быть доступны всем процессам без использования коммуникационной среды.

В исходном алгоритме обучения количество корректировок равно количеству обучающих примеров, а в выборочном оно равно количеству неправильно распознаваемых примеров. По мере обучения число неправильных распознаваний снижается, что приводит к уменьшению корректировок нейронной сети и может служить основанием для эффективного распараллеливания алгоритма обучения обратным распространением ошибки.

На рис. 4 представлена диаграмма среднего количества корректировок параметров нейронной сети (шкала C в логарифмическом масштабе) при обучении на выборках различного объема. При использовании выборочного алгоритма всегда требуется меньшее число корректировок. Из диаграммы так же видно, что рост количества корректировок у выборочного алгоритма с ростом числа обучающих примеров происходит медленней: зависимость линейная, в то время как у исходного алгоритма зависимость носит степенной характер. Это говорит о возможности эффективного распараллеливания при большом объеме обучающей выборки, что существенно для решаемой задачи.

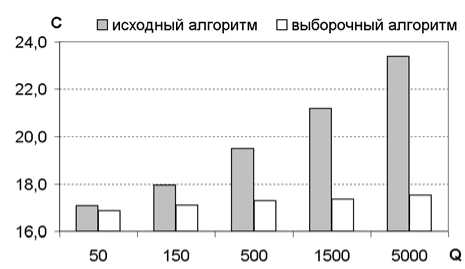
Рис. 4. Среднее число корректировок при обучении нейронной сети. Q – количество обучающих примеров; C = log2K, где K – количество корректировок за все время обучения

Заключение

Обучение нейронной сети по алгоритму обратного распространения ошибки только на неправильно распознаваемых примерах, несмотря на опасность «забывания» ранее обученным образам, выгодно со многих сторон. Уменьшается вероятность того, что сеть застрянет в локальном минимуме поверхности функции оценки. Снижается время обучения нейронной сети. Количество корректировок параметров сети во время обучения так же умень- шается, что при распараллеливании алгоритма для вычислительных систем типа кластеров приведет к снижению необходимых операций обмена. Этот эффект особенно заметен при большом количестве обучающих примеров, т.е. там, где наиболее важна возможность распараллеливания.