Условия исправления сферической аберрации третьего порядка в шарообразной линзе со сферическим распределением показателя преломления
Автор: Ильинский Р.Е.
Журнал: Компьютерная оптика @computer-optics
Рубрика: Дифракционная оптика, оптические технологии
Статья в выпуске: 6 т.46, 2022 года.
Бесплатный доступ
Рассмотрена шарообразная линза. Показатель преломления этой линзы является функцией расстояния от центра шара. Получены условия, при которых такая линза свободна от сферической аберрации третьего порядка, если на линзу падает параллельный пучок лучей.
Градиентная оптика, линза люнебурга, аберрации третьего порядка, численное интегрирование
Короткий адрес: https://sciup.org/140296235
IDR: 140296235 | DOI: 10.18287/2412-6179-CO-1104
Текст научной статьи Условия исправления сферической аберрации третьего порядка в шарообразной линзе со сферическим распределением показателя преломления
Среди сред с неоднородным распределением показателя преломления особое место занимают среды, показатель преломления которых зависит только от расстояния до фиксированной точки. Так как эквирефракционные поверхности в такой среде являются сферами, то такие среды носят название сред со сферическим распределением показателя преломления.
Изучение оптических свойств сред со сферическим распределением показателя преломления имеет давнюю историю [1]. Это связано с тем, что распределение показателя преломления в земной атмосфере и ряда биологических объектов близко к сферическому [2, 3]. При исследовании оптических свойств сред со сферическим распределением показателя преломления очень важные результаты были получены Максвеллом [4, 5] и Люнебургом [6]. Результаты работы [6] позднее были обобщены в статье [7] и стали известны как уравнения, описывающие обобщенную линзу Люнебурга [8, 9, 10, 11]. Линза Люнебурга имеет форму шара, центр которого совпадает с центром симметрии распределения показателя преломления. Закон изменения показателя преломления обеспечивает полное устранение сферической аберрации для падающего на линзу пучка лучей. Хотя в менискообразной линзе Ильинского [12] также обеспечивается полное устранение сферической аберрации, но в работе [13] указаны преимущества линзы Люнебурга перед другими линзами из материала со сферическим распределением показателя преломления.
В настоящее время линза Люнебурга используется во многих устройствах микроволновой техники [14, 15, 16, 17, 18, 19, 20]. Это обусловлено тем, что в микроволновой технике возможно изготовление деталей из материалов, показатель преломления которых меняется в достаточно широком интервале. Оптические системы, которые преобразуют излучение видимого и ближнего инфракрасного диапазонов, также могут быть построены на основе шарообразных линз со сферическим распределением показателя преломления [21, 22, 23]. Но при проектировании подобных линз необходимо учитывать ограничения, которые накладывает технология получения соответствующих материалов [24, 25, 26, 27, 28, 29, 30, 31, 32]. А использование формул, по которым рассчитывается показатель преломления в обобщенной линзе Люнебурга, часто приводит к нереализуемым или очень трудно реализуемым в видимом и ближнем инфракрасном диапазонах распределениям показателя преломления [33, 34]. Поэтому в настоящей статье для исследования оптических характеристик шарообразной линзы со сферическим распределением показателя преломления используется параксиальное приближение и теория аберраций третьего порядка [1]. Хотя такой подход не обеспечивает полного устранения аберраций, но позволяет достаточно просто найти примерный вид распределения показателя преломления и оценить его технологичность. Полученное распределение показателя преломления может быть использовано в качестве первого приближения при поиске оптимального (как с точки зрения остаточных аберраций, так и с точки зрения технологии) решения методами компьютерной оптимизации [35].
В данной статье будет рассмотрен представляющий наибольший интерес случай, когда на линзу падает параллельный пучок лучей. Однако представленные в статье методы можно обобщить на случай, когда на линзу падает сходящийся или расходящийся пучок лучей.
Основные оптические характеристики среды со сферическим градиентом показателя преломления
Пусть в системе координат XYZ показатель преломления описывает функция
n ( x , у , z ) = n 0 д/1 + g ( x 2 + y 2 + z 2) + f ( x 2 + y 2 + z 2)2, (1)
где n 0 , g , f - параметры распределения показателя преломления. При малых значениях x , у функцию (1) можно аппроксимировать выражением
n ( x , у , z ) * П о ( z ) + П 1 ( z )( x 2 + у 2) + П 2 ( z )( x 2 + у 2)2, (2)
где
П о ( z ) = n (0,0, z ) = n о ^/ 1 + g z 2 + f
, a 1
n 1 ( z ) = 2
" ■ ( z ) = 4i
d 2 n ( x , у , z )
ау2 x d4 n (x, у, z) dу4
z4, n o(g + 2 f z2)
2^1 + g z 2 + f z 4
= n о (4 f - g 2)
8(1 + g z 2 + f z 4)32
В параксиальном приближении траекторию луча у = h ( z ), x = 0 в среде с распределением показателя преломления (2) описывает система дифференциальных уравнений [1]
-d h ( z ) = -a ( z ), (6)
d z
Т-[ П о ( z ) a ( z )] = - 2 П 1 ( z ) h ( z ). (7)
d z
Решение системы дифференциальных уравнений (6), (7) представим в виде:
h ( z ) = П с ( z )( h 0 +« 0 z 0 )
----+ 2 z 3 . По ( z )
a ( z ) = « 0 - 2 П 0 ( z )( h 0 + « 0 z 0 ) 3 ,
где « 0 = a ( z 0 ), h 0 = h ( z 0 ),
-« 0 z ,
g z + f z 3 - g z 0 + f z 0 3 - f r z Z 2d Z 2 П 0 ( z ) 2 П 0 ( z ) 2 J z = 0 П о ( £ )'
Шарообразная линза со сферическим распределением показателя преломления
На рис. 1 показана линза, которая представляет ограниченную сферической поверхностью с радиусом r среду с показателем преломления (1). Обе преломляющие поверхности такой шарообразной линзы являются эквирефракционными.
По [36] радиус кривизны первой преломляющей поверхности линзы равен r 1 = r , радиус кривизны второй преломляющей поверхности линзы равен r 2 = r . На первой преломляющей поверхности луч преломляется из среды с показателем преломления 1 в среду с показателем преломления (1). На второй преломля-
ющей поверхности луч преломляется из среды с показателем преломления (1) в среду с показателем преломления 1.
Траектория луча в параксиальном приближении
Пусть входной участок траектории луча лежит на прямой у = h о , x = 0.
В параксиальном приближении направление траектории луча после преломления на первой поверхности линзы характеризует значение [1]
a ( - r ) = « о = h П—1, r n r
где
п r = n 0 1 + g r 2 + f r 4.
При подстановке z 0 = - r , z = r в выражения (8), (9) получим
h2 = h(r) = h0f 2 ^ -1 - rf Гr Z2dZ n02 n0 J-r ^ 1 + g Z2 + f Z4 у
2 Пr + f rr Z2dZ rn02 n0 J-r 1 + g Z2 + f Z4 у
\
1 f 1 , 1 a(r) = h - +--- r r П r
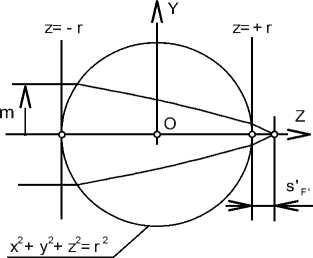
Рис. 1. Шарообразная линза со сферическим распределением показателем преломления
)
,(12)
Эти значения соответствуют конечной точке участка траектории луча в градиентной среде.
В параксиальном приближении выходной участок траектории луча (т. е. после преломления на второй поверхности линзы) лежит на прямой у = h 2 - a"(z - r), x = 0, где [1]
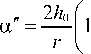
_ ^L fl + r z 2d Z
+ h 0 .
n 0 2 У n 0 J- r 1 1 + g Z 2 + f Z 4
Заднее фокусное расстояние f ' и задний фокальный отрезок 5 F 1 линзы равны [1]
h о , h '2
, 5 F' = a" a"
Представим величину g в виде
g = -
- n 2 + П 0 2 f + n 2 n 0 2 r 2
Д . „=- fm 2 , (21)
2 h 0 4
где f = f r 4.
Пусть h 2 = hok ,
где к - безразмерный коэффициент. Тогда из формулы (12) следует
f = [ 2 П о^- 1 -к| n , I n о 2 J O ( f )
где
~ p + 1
O(f)= J - 1
___________ Z 2 dZ ___________ v к 4 - ( f - n 2/ n 0 + 1) Z 2 + 1
Из равенств (18), (17) и формул (15) следует
r
1 -k ’
, к
5 ‘- = Г ------.
F 1 -к
где m - высота падения луча на первую поверхность,
S Σ = S 1 + S ∗ + S 2 ,
, (23)
Из равенства (18), выражения (16) и формул (22– 26), (A.2) следует
Сферическая аберрация третьего порядка
Продольная сферическая аберрация третьего пo-рядка рассматриваемой линзы равна [1]
S , = h^ P ( n 0 , n r ) ,
где
- f c+ 1 4 r+ 1 3
P ( n 0 , n r ) = —Ш - d z n o n r f J ------------------------ z^T d Z ] +
3 n о - 1 ^f Z 4 - ( f - n 2 / n о + 1 ) z 2 + 1 -[ f Z 4 - ( f - n 2 / n 0 2 + 1 ) z 2 + 1 ]
+—-— ( + 8 f K n 0 2 n r + 8 f n 0 n r - 8 к п 3 - 8 n r + 8 n 2 - к 3 n 04 n r + 3 k 2 n 0 n r - З к п 0 n r - n 0 n r + 8 K n 0 n r + 8 n 0 2 n r - 6 n 0 2). 3 n 04 n r
Значение f в формуле (28) является корнем уравнения (18).
Аппроксимация значений интегралов
Для приближенного вычисления значений интегралов в формулах (18), (28) используем выражения [37]:
Г1 Z 2 d Z . 2 ( 2 n r + 3 n 0) , (29)
-
L1 fZ4-(f - n 2/ n 02 + 1)z2 +1 15n r’
t+1
J /d
-
1 f 4 - ( f - n 2 / n о + 1 ) z 2 + 1
+ 1
-
-J-1--------------------------------- dz..(30)
[ f Z 4 - ( f - n 2 / n о + 1 ) z 2 + 1 ] 2
-
2 ( 2 n 3 + 4 n 0 n 2 - 3 n 0 )
®
3 n r 3
Из формул (29), (18) следует, что первое приближение для ~ f можно принять равным f = 15n r
2 n 0
2 n r - ( k + 1 ) n 0
2 n r + 3 n 0
При подстановке формул (31, 30) в выражение (28) получим
P ( n 0, n r )® Pappr ( n 0, n r ),(32)
где
, ( 6 n 0 - 24 п Г п o - 8 n 2 n 0 - 4 n 3 ) f
Pappr (n 0,n r ) = ~ 3 3
9 n 3 r n 0 3
-
3 n r n 0 4 - 24 n r n 0 2 + 18 n 0 2 + 24 n r - 24 n 2
9 n r n 04
8 n0 f - 3 n4 + 8 n0 - 8 n 2 к3,
-к+к2. 3n043
Специальный случай
Распределение показателя преломления при f =0 является наиболее технологичным. Если f =0, то из формулы (18) следует k= 2nr n0 . (34)
n 0 2
После подстановки выражения (34) в формулы (20), (27) получим
|
f ' = n 0 2 r |
(35) |
|
2 ( n r - n2 ) , ( 2 nr - n 2 2 ) r |
|
|
5 = -^ 2 ( n r - n 0 ) ’ |
(36) |
|
P ( n 0 , n r ) = P 0 ( n 0 , n r ) , |
(37) |
где
P o ( n 0 , n r ) = ——[4 n 4 - 4 n 2 n r + 4 n 4 n 2 - ....
n 0 6 n r (38)
- 4 n 0 2 n 2 - n 06 n r + n 4 ].
Из формулы (36) следует, что задний фокальный отрезок равен нулю при n r = n 2 /2 и становится бесконечно большим при n r = n 2 . Если выполняется условие
2 n 0 2
< n r < n 0 ,
то задний фокальный отрезок будет положительным. Из формулы (37) следует, что сферическая аберрация будет исправлена в случае, когда P 0 ( n 0 , n r ) =0. График функции P 0 ( n 0 , n r ) показан на рис. 2. График построен для диапазона значений n 0 [1,4; 2] и n r [1,4; 2], что соответствует реально достижимым значениям показателей преломления градиентных сред, используемых в видимом и ближнем инфракрасном диапазонах. Однако реальные значения перепада показателя преломления | n r – n 0 | обычно не превышают 0,2 (чаще 0,05). На рис. 3 показана линия нулевых значений функции P 0 ( n 0 , n r ), парабола n r = n 2 /2 и линия n ? = n 0 .
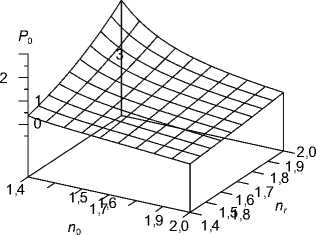
Рис. 2. График функции P 0 (n 0 , n r )
Условия исправления сферической аберрации третьего порядка
На рис. 4 в системе координат ( n 0 ; n r ) показаны пунктиром линии нулевых значений функции P appr ( n 0 , n r ) при к = 0 ( 5'F■ = 0) и при к =0 , 2 ( 5'F' = r/ 4). Для этих же двух значений κ сплошными линиями соединены точки, где функция P ( n 0 , n r ) принимает нулевые значения. Точки 1, 2, 3, 4, 5, 6 лежат на линии нулевых значений функции P ( n 0 , n r ) при к = 0. Точки 7, 8, 9, 10, 11 лежат на линии нулевых значений функции P ( n 0 , n r ) при к = 0 , 2.
Расчет значений функции P (n0, nr) производился следующим методом. Первое приближение для f находилось по формуле (31). Для уточнения f из уравнения (18) была получена рекуррентная формула
/V f k+1
2 n" - 1 -к] n , n 2 J Q ( f k )
где k = 1 , 2 , 3 , . . . , а ~ f 1 соответствует первому приближению. Для вычисления Q ( ~ f k ) использовался метод Симпсона [37] с шагом 0,002. Условие окончания уточнения значения ~f имеет вид || f k- f k + 1 1| < 0 , 001. Полученное значение f используется при вычислении интегралов в формуле (28) методом Симпсона с шагом 0,002.
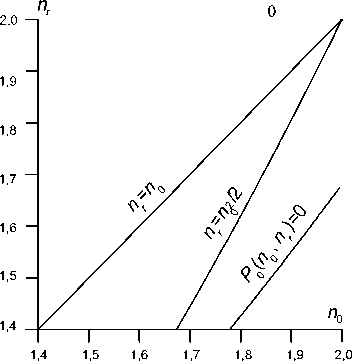
Рис. 3. Линия нулевых значений функции P 0 (n 0 , n r ), парабола n r = n 2 /2 и линия n r = n 0
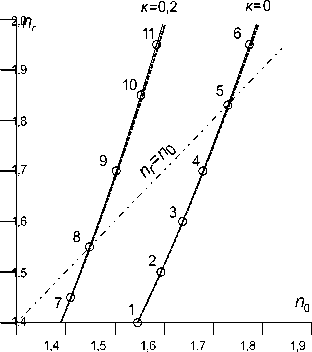
Рис. 4. Линии нулевых значений функций P(n 0 , n r )
[сплошные линии] и P « (n c , n r ) [пунктир] при к = 0 и к = 0,2
На рис. 5 показаны графики функций распределений показателей преломления, которые соответствуют точкам 1, 2, 3, 4, 5, 6 на рис. 4.
На графике, который отмечен цифрой 3, точка экстремума функции распределения показателя преломления находится на поверхности шара. На рис. 6 показаны графики функций распределений показате- лей преломления, которые соответствуют точкам 7, 8, 9, 10, 11 на рис. 4.
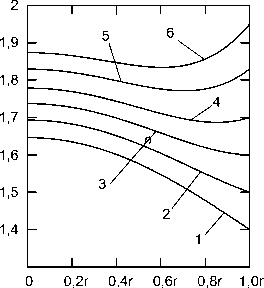
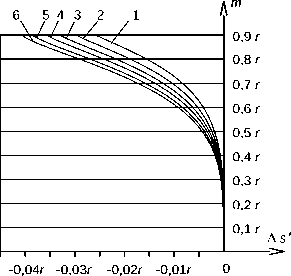
Рис. 7. Продольная сферическая аберрация шарообразных линз с исправленной сферической аберрацией третьего порядка и sF ’ = 0
z
Рис. 5. Распределения показателя преломления, которые обеспечивают устранение сферической аберрации третьего порядка при s f ' = 0
Продольная сферическая аберрация реальных лучей
На рис. 7 показаны графики продольной сферической аберрации для шарообразных линз с распределениями показателей преломления, которые соответствуют точкам 1, 2, 3, 4, 5, 6 на рис. 4. На рис. 8 показаны графики продольной сферической аберрации для шарообразных линз с распределениями показателей преломления, которые соответствуют точкам 7, 8, 9, 10, 11 на рис. 4. Графики на рис. 7, 8 построены на основе расчета траекторий реальных лучей в программе ZEMAX [38]. Все графики на рис. 7, 8 имеют вид, который характерен для случая, когда отсутствует расфокусировка, полностью исправлена сферическая аберрация третьего порядка, но имеют место значительные аберрации высших порядков [39]. Поэтому, как уже было отмечено выше, распределение показателя преломления, которое получено из условия полного устранения сферической аберрации третьего порядка, должно рассматриваться не как окончательный вариант, а только как исходный вариант для компьютерной оптимизации.
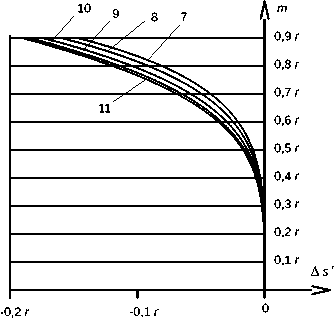
Рис. 8. Продольная сферическая аберрация шарообразных линз с исправленной сферической аберрацией третьего порядка и s ' f ' = r/4
Демонстрация использования методов компьютерной оптимизации
С целью демонстрации возможности исправления продольной сферической аберрации методом компьютерной оптимизации на рис. 9 представлены графики продольной сферической аберрации трех шарообразных линз. Показатель преломления первой и второй линзы описывается функцией (1). Показатель преломления третьей линзы описывается функцией
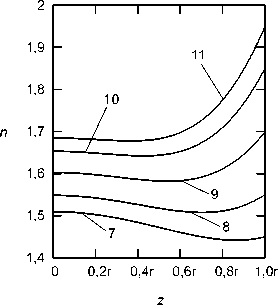
Рис. 6. Распределения показателя преломления, которые обеспечивают устранение сферической аберрации третьего порядка при s ' f = r/4
n ( x, y, z ) =
= n 0 [1 + g ( x 2 + y 2 + z 2 ) + f ( x 2 + y 2 + z 2 ) 2 +
+ b 1 ( x 2 + y 2 + z 2 ) 3 + b 2 ( x 2 + y 2 + z 2 ) 4 +
+ b з ( x 2 + y 2 + z 2) 5 ]1/2,
где n 0 , g , f , b 2 , b 3 – параметры распределения показателя преломления. Распределение показателя преломления первой линзы соответствует графику, который отмечен цифрой 2 на рис. 4. Параметры g , f распределения показателя преломления второй линзы и параметры g , f , b 2 , b 3 распределения показателя преломления третьей линзы определены при помощи процедуры оптимизации программы Zemax [38]. Целью оптимизации было выбрано достижение минимальных значений продольной сферической аберра-
ции при максимально допустимом значении показателя преломления на поверхности шара 1,7. Исходным вариантом распределения показателя преломления для процедур оптимизации было задано распределение показателя преломления, которое соответствует отмеченному цифрой 2 графику на рис. 4 (т. е. распределение показателя преломления первой линзы). Параметры распределения показателя преломления в линзах приведены в табл. 1.
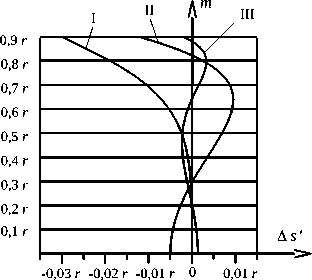
Рис. 9. Продольная сферическая аберрация первой (I), второй (II) и третьей (III) шарообразных линз
Табл. 1. Параметры распределения показателя преломления в линзах
|
Первая линза |
Вторая линза |
Третья линза |
|
|
n 0 |
1,6932827 |
1,6932827 |
1,6932827 |
|
g / r 2 |
– 0,92813181 |
– 1,1000961 |
–0,97593872 |
|
f / r 4 |
0,31092542 |
0,72611026 |
–0,63606382 |
|
b 1 / r 6 |
1,6694156 |
||
|
b 2 / r 8 |
0,94822734 |
||
|
b 3 / r 10 |
–0,98284441 |
Заключение
Исследуется проблема исправления сферической аберрации третьего порядка в шарообразной линзе со сферическим распределением показателя преломления. Получены выражения для расчета сферической аберрации третьего порядка в данной линзе. На основе этих выражений рассчитано несколько распределений показателя преломления, которые обеспечивают полное исправление сферической аберрации третьего порядка при условии, что значение показателя преломления в любой точке линзы больше или равно 1,4 и меньше или равно 2. Исправление сферической аберрации третьего порядка подтверждено расчетом реальных лучей через шарообразные линзы.
Рассмотрен случай, когда показатель преломления описывается функцией n (x, y, z) = n 0 ^ 1 + g (x2 + y2 + z2), где g = (n2 / n0 -1) / r2.
Доказано, что в этом случае при n о е [1 , 4; 2] и n r е [1 , 4; 2] невозможно одновременно исправить сферическую аберрацию и получить положительное значение заднего фокального отрезка (см. рис. 3).
Список литературы Условия исправления сферической аберрации третьего порядка в шарообразной линзе со сферическим распределением показателя преломления
- Marchand EW. Gradient index optics. New York, San Francisco, London: Academic Press; 1978.
- Lehn WH. Isaac Newton and the astronomical refraction. Appl Opt 2008; 47(34): H95-H105. DOI: 10.1364/AO.47.000H95.
- Matthiessen L. Ueber die Beziehungen, welche zwischen dem Brechungsindex des Kerncentrums der Kry stalllinse und den Dimensionen des Auges bestehen. Pfüger's Archiv für die gesamte Physiologie des Menschen und der Tiere 1882; 27: 510-523.
- Maxwell JC. Problems 3. Cambr Dublin Math J 1854; 8: 188.
- Maxwell JC. On the general laws of optical instruments. The Quarterly Journal of Pure and Applied Mathematics 1858; 2: 233-246.
- Luneburg RK. Mathematical theory of optics. Providence, Rhode Island: Brown University; 1944.
- Fletcher A, Murphy T, Young A. Solution of two optical problems. Proc R Soc London Ser A 1954; 223(13): 216-225.
- Doric S, Munro E. General solution of the nonfull-aperture Luneburg lens problem. J Opt Soc Am 1983; 73(8): 10831086.
- Gordon JM. Spherical gradient-index lenses as perfect imaging and maximum power transfer devices. Appl Opt 2000; 39(22): 3825-3832.
- Colombini E. Index-profile computation for the generalized Luneburg lens. J Opt Soc Am 1981; 71(11): 14031405. DOI: 10.1364/JOSA.71.001403.
- Kotlyar VV, Melekhin AS. Abel transform to calculate the gradient of optical elements with spherically symmetric distribution of the refractive index. Computer Optics 2002; 24: 48-52.
- Ilinsky R. Gradient-index meniscus lens free of spherical aberration. J Opt A-Pure Appl Opt 2000; 2(5): 449-451. DOI: 10.1088/1464-4258/2/5/316.
- Demetriadou A, Hao Y. Slim Luneburg lens for antenna applications. Opt Express 2011; 19(21): 19925-19934. DOI: 10.1364ЮЕ.19.019925.
- Leng LY, Yang Y, Wang N, Ma YG, Ong CK. Broadband microwave Luneburg lens made of gradient index metamaterials. J Opt Soc Am A 2012; 29(4): 426-430. DOI: 10.1364/JOSAA.29.000426.
- Ruiz-Garcia J, Martini E, Giovampaola CD, González-Ovejero D, Maci S. Reflecting Luneburg lenses. IEEE Trans Antennas Propag 2021; 69(7): 3924-3935. DOI: 10.1109/TAP.2020.3044668.
- Bahr RA, Adeyeye AO, Van Rijs S, Tentzeris MM. 3D-Printed omnidirectional Luneburg lens retroreflectors for low-cost mm-wave positioning. 2020 IEEE Int Conf on RFID (RFID) 2020: 1-7. DOI: 10.1109/RFID49298.2020.9244891.
- Ansari M, Jones B, Guo YJ. Spherical Luneburg lens of layered structure with low anisotropy and low cost. IEEE Trans Antennas Propag 2022: 1-1. DOI: 10.1109/TAP.2022.3140509.
- Biswas S, Lu A, Larimore Z, Parsons P, Good Au, Hudak N, Garrett B, Suarez J, Mirotznik MS. Realization of modified Luneburg lens antenna using quasi-conformal transformation optics and additive manufacturing. Microw Opt Technol Lett 2019; 61(4): 1022-1029. DOI: 10.1002/mop.31696.
- Lu H, Liu Z, Liu Y, Ni H, Lv X. Compact air-filled Luneburg lens antennas based on almost-parallel plate waveguide loaded with equal-sized metallic posts. IEEE Trans Antennas Propag 2019; 67(11): 6829-6838. DOI: 10.1109/TAP.2019.2927862.
- Kadéra P, Sánchez-Pastor J, Eskandari H, Tyc T, Sakaki M, Schüßler M, Jakoby R, Benson N, Jiménez-Sáez A, Lácík J. Wide-angle ceramic retroreflective Luneburg lens based on quasi-conformal transformation optics for mm-wave indoor localization. IEEE Access 2022; 10: 4109741111. DOI: 10.1109/ACCESS.2022.3166509.
- Suzuki M, Hattori J. Gradient index lens. US Patent 4848882 of July 18, 1989.
- Liang R, Kessler D. Monocentric autostereoscopic optical apparatus with a spherical gradient index ball lens. US Patent 6940645B2 of September 06, 2005.
- Handerek VA, Laycock LC. Retroreflective device comprising gradient index lenses. US Patent 7170688B2 of January 30, 2007.
- Koike Y, Kanemitsu A, Shioda Y, Nihei E, Ohtsuka Y. Spherical gradient-index polymer lens with low spherical aberration. Appl Opt 1994; 33(16): 3394-3400. DOI: 10.1364/A0.33.003394.
- Singer W, Testorf M, Brenner K-H. Gradient-index micro-lenses: numerical investigation of different spherical index profiles with the wave propagation method. Appl Opt 1995; 34(13): 2165-2171. DOI: 10.1364/AO.34.002165
- Yi Y, Zhang Y, Ru X, Dong L. The manufacture of polymer gradient refractive index spherical microlens. Acta Photonica Sinica 2003; 32(4): 425-428. DOI: 10.1023/A:1022289509702.
- Bukhbinder TL, Dremina EA, Kosyakov VI, Moryganov AN, Tukhvatulin ASh. Basic rules for the formation of a refractive index profile in planar polymer structures. Tech Phys 1997; 42(4): 399-402.
- Ji S, Yin K, Mackey M, Brister A, Ponting M, Baer E. Polymeric nanolayered gradient refractive index lenses: technology review and introduction of spherical gradient refractive index ball lenses. Opt Eng 2013; 52(11): 112105. DOI: 10.1117/1 .OE.52.11.112105.
- Sasan K, Lange A, Yee TD, Dudukovic N, Nguyen DT, Johnson MA, Herrera OD, Yoo JH, Sawvel AM, Ellis ME, Mah CM, Ryerson R, Wong LL, Suratwala T, Destino JF, Dylla-Spears R. Additive manufacturing of optical quality germania-silica glasses. ACS Appl Mater Interfaces 2020; 12(5): 6736-6741. DOI: 10.1021/acsami.9b21136.
- Cooperstein I, Shukrun E, Press O, Kamyshny A, Magdassi S. Additive manufacturing of transparent silica glass from solutions. ACS Appl Mater Interfaces 2018; 10(22): 18879-18885. DOI: 10.1021/acsami.8b03766.
- Assefa BG, Pekkarinen M, Partanen H, Biskop J, Turunen J, Saarinen J. Imaging-quality 3D-printed centimeter-scale lens. Opt Express 2019; 27(9): 12630-12637. DOI: 10.1364/0E.27.012630.
- Dylla-Spears R, Yee TD, Sasan K, Nguyen DT, Dudukovic NA., Ortega JM, Johnson MA, Herrera OD, Ryerson FJ, Wong LL. 3D printed gradient index glass optics. Sci Adv 2020; 6(47): eabc7429. DOI: 10.1126/sciadv.abc7429.
- Kotsidas P, Modi V, Gordon JM. Gradient- index lenses for near-ideal imaging and concentration with realistic materials. Opt Express 2011; 19(16): 15584-15595. DOI: 10.1364/OE.19.015584.
- Kotsidas P, Modi V, Gordon JM. Gradient-index lenses for near-ideal imaging and concentration with realistic materials: errata. Opt Express 2012; 20(1): 338-338. DOI: 10.1364/OE.20.000338
- Gross H (ed.), Zügge H, Peschka M, Blechinger F. Handbook of optical systems. Vol 3: Aberration theory and correction of optical systems. Weinheim: WILEY-VCH Verlag GmbH & Co KGaA; 2007.
- GOST 7427-76. Geometrical optics. Terms, definitions and letter symbols [In Russian]. Moscow: USSR State Committee on Standards; 1988.
- Krylov VI. Approximate calculation of integrals. Dover Publications Inc; 2005.
- ZEMAX optical design program: Users guide. Zemax Development Corporation; 2010.
- Smith W. Modern optical engineering. 4th ed. McGraw-Hill; 2007.


