Условия синхронизации численности двух взаимосвязанных сообществ (на основе модели Лотки-Вольтерра)

С начала XX в. активно развивается динамическая теория биологических популяций, в рамках которой исследуются закономерности изменения численности особей взаимодействующих биологических видов, в частности, условия возникновения устойчивых колебаний. Биологическая популяция понимается как совокупность особей одного вида, проживающих на некоторой ограниченной территории. Для описания динамики таких популяций необходимо использовать нелинейные модели, учитывающие основные факторы их развития (рождаемость, смертность, межвидовые взаимодействия, миграция).

Первое глубокое математическое исследование моделей биологических сообществ, включающих в себя несколько популяций различных видов, и изучение закономерностей динамики их взаимодействия дано в книге В. Вольтерра «Математическая теория борьбы за суще-ствование»(1931) [3].

В дальнейшем такие работы стали развиваться по двум направлениям. Представители первого направления для описания функций, входящих в модель, задавали лишь их качественные особенности, такие как положительность, монотонность отношения типа больше меньше [4, 16]. Примером служит работа АН. Колмогорова, который рассмотрел обобщенную модель взаимодействия биологических видов типа «хищник-жертва» или «паразит-хозяин» [4]. Исследование этой модели и ее частных случаев привело к выводу о том, что, если численность хищника ограничивается наличием жертвы, в системе имеют место регулярные колебания. Если численность жертвы ограничивается количеством необходимых ей ресурсов, или численность хищника ограничивается не количеством жертвы, а другим фактором, это приводит к затухающим колебаниям.

В рамках второго направления рассматривались различные модификации системы Вольтерра, полученные посредством включения в исходную систему различных дополнительных факторов и закономерностей, описываемых явными функциями. Использование компьютер ной техники позволило применить полученные результаты к конкретным популяциям, в частности, в задачах оптимального промысла [2, 9,11,15].

К настоящему времени в разных странах и в разных изданиях опубликовано большое количество работ, авторы которых рассматривают те или иные конкретные задачи теории биологических популяций ирешают их различными методами [5-7,10,12-14]. Широкое распространение получили методы, основанные на теории дифференциальных и разностных уравнений [5, 6,12-14].

Особый интерес представляет выявление условий синхронизации [12, 14] изменений численностей двух или многих сообществ, заселяющих соседние регионы и взаимодействующих между собой за счет миграции особей [6,12,14].

В настоящей работе исследование данного вопроса будет основываться на методах математического моделирования и теории дифференциальных уравнений, позволяющих определить основной характер траекторий системы, расположение особых точек, их устойчивость, характер поведения траекторий вблизи особых точек [1,8].

Основное внимание в работе уделяется определению условий синхронизации колебаний численности рассматриваемых сообществ, связанных с влиянием миграционного взаимодействия между сообществами на динамику каждой популяции.

Построение модели миграционно-свжанных сообществ

Одной из важнейших характеристик популяции при изучении динамики ее развития является общая численность особей. Построим и исследуем модификацию модели Лотки-Вольтерра, являющуюся автоколебательной. Рассмотрим два сообщества «хищник-жертва», заселяющих соседние регионы и взаимодействующие между собой за счет локальной миграции хищника. Обозначим через хр у: и хр у2 соответственно общую численность популяции жертвы и хищника в первом и во втором регионе в момент времени t. Предположим, что все особи, составляющие каждое сообщество, заселяют два полностью идентичных местообитания таким образом, что демографические параметры и параметры взаимодействия оказываются также идентичными. Буцем считать, что количество мигрантов из одной территории в другую составляет постоянную долю от численности (плотности) хищника для того местообитания, откуда идут мигранты. При этом буцем пренебрегать возможной смертностью особей в процессе миграции либо буцем считать, что она неявно включена в общую смертность. Следовательно, доли мигрантов также оказываются равными. Тогда уравнения динамики численности двух миграционно-связанных сообществ можно записать в виде:

Ё = ^ - АЛ

Т1 = -Ж + Р^\У\ + ^тУг - ту_х

Д = гхг-ухгуг

>2 = -/^2 + РЧУг + ^тУг ~ ^тУг

О)

где г- скорость размножения популяции жертвы в отсут-ствиихищника, у-удельная скорость потребления популяцией хищника популяции жертвы при единичной плотности обеих популяций, //- естественная смертность хищника, р! у- коэффициент переработки потребленной хищником биомассы жертвы в собственную биомассу, т - коэффициент миграции хищника (доля).

В исходной записи система (1) содержит пять независимых параметров. Заменой переменных:

^xi (О ^—         , У г    ^— К (^г), t = — i= 12

р            Уг приходим к системе уравнений:

Mi = Mi - МТТ1 иmm

Vi = - — Vi + Mi Vi + — v₂ - — Vi r r

Z/ 2 — ^2^2^2

Umm v2 =--v2 + M2v2 + — VT--v2 r              r r

Введя обозначения a = —, b = —, получаем систему г г с двумя параметрами:

Mi = Mi - МТТ1

Vi = -«Vi +M1V1 + bv2 -6vi m2 = m2 -M2v2             .        (2)

v₂ = —av₂ + m₂v₂ + bv_x - bv₂

Коэффициенты модели в каждом случае имеют конкретный биологический смысл: а - относительная скорость роста численности хищника, равная отношению скорости гибели хищника и скорости прироста жертвы, Ъ - относительная доля миграции хищника, равная отношению доли мигрантов хищника и скорости прироста жертвы.

Исследуемая система (2) имеет четыре особые точки. Первая особая точка (0,0,0,0), соответствующая нулевым численностям особей в обоих сообществах, является седлом при любых значениях коэффициентов. Вторая особая точка (а, 1,^,1) соответствует одновременному существованию двух видов в обеих популяциях с ненулевой численностью. Две последние особые точки являются седлом и соответствуют нулевой численности жертвы u=Q на первой территории (или м2=0 во втором регионе соответственно).

Из аналитического выражения собственных чисел якобиана системы (2) в окрестности особых точек следует, что если выполняется условие Ь²<а, то численности популяций имеют затухающие колебания во времени, соответствующие ненулевой особой точке (а, 1, а, 1) типа устойчивый фокус. При выполнении условия Ъ²=а особая точка буцет лежать на границе между областями устойчивых фокусов иузлов.

При Ъ²>а особая точка становится устойчивым узлом. При этом численности популяций совершают во времени незатухающие периодические колебания, а в фазовом пространстве вокруг ненулевой особой точки образуются замкнутые концентрические кривые - центры.

Как уже сказано, колебания численности в рассматриваемой модели (2), состоящей из двух связанных систем типа хищник-жертва, носят автоколебательный характер. Если их изолировать друг от друга (при b=Q\ то они буцут продолжать генерировать колебания в собственном ритме, который полностью определяется свойствами (значением параметров) самой системы. За счет миграции хищника эти сообщества подстраивают свои ритмы, например, если численность одной из популяций рассматриваемых сообществ медленно изменяется, то численность популяций второго сообщества следует за этим изменением.

В связи с этим, далее исследуются условия синхронизации колебаний двух соседних миграционно-связанных сообществ, сформулированные в терминах теории синхронизации связанных нелинейных осцилляторов [1,8]. В данной работе под синхронизацией понимается максимально широкое ее значение - подстройка ритмов (совпадение частот колебаний), которая может сопровождаться совпадением фаз и амплитуц колебаний.

Исследование синхронизации колебаний численности

На начальном этапе исследования рассмотрим две идентичные подсистемы, следовательно, частоты коле-банийу них изначально буцут совпадать. В случае, когда отсутствует миграционная связь (параметр связи b=Q\ получаем систему вида:

Mi = Mi - МТТ1

Vi = —avy + м^

м₂ = m₂ -m₂v₂ (3)

v₂ = —av₂ + m₂v₂

Приходим к системе Вольтера «хищник-жертва», в которой две популяции существуют вне зависимости друг от друга. Такая система имеет четыре особые точки: три из них (0,0,0,0), (а, 1,0,0), (0,0,а, 1) являются седлом с равными собственными числами ДаД^аДХ четвертая (a, l,a, 1) - центром с собственным числом

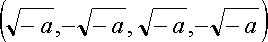
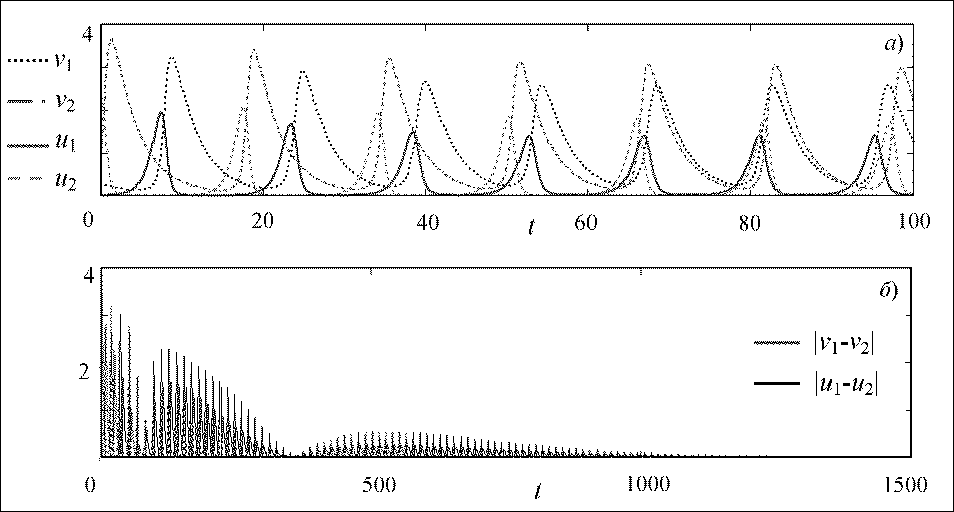
Рис. 1. Динамика системы (2) при b = 0,005 (а), разности моментальных амплитуд двух сообществ (б)

Полученная система состоит из двух автономных консервативных подсистем, каждая из которых генерирует свои собственные колебания. Ввиду отсутствия параметра связи, фазовые переменные этой системы оказываются независимыми и как следствие не могут подстроить свои ритмы.

Рассмотрим особую точку (а, 1 ,а, 1), которая соответствует одновременному существованию двух сообществ, особи которых связаны отношениями типа «хищник-жертва», заселяющих соседние регионы. Выберем фиксированное значение относительной скорости роста хищника а =0,3 численности хищника.

Рассмотрим следующие начальные условия: w₁(0)=0,02635, v₁(0)=0,98918, н₂(0)=0,19907, v₂(0)=0,46408, соответствующие максимальным и минимальным значениям численности жертвы и на фазовой кривой системы (3) типа центр.

При существовании двух соседних не связанных друг с другом сообществ (относительная доля миграции Ь=0), синхронизация их колебаний не наблюдается, это подтверждается тем, что динамики численности особей рассматриваемых сообществ не совпадают с течением времени. Графики разности моментальных амплитуц колеблются в полосе от 0 до 4 (не падают до нуля), следовательно, развитие рассматриваемых сообществ происходит асинхронно. Фазовые портреты системы (3) представляют собой концентрические замкнутые кривые (центры), по которым точка движется против часовой стрелки. Полный период колебаний решения системы (3) при а=0,3 составляет Г=18.

В случае, когда рассматриваемые сообщества слабо связаны друг с другом (относительная доля миграции 6=0,005 системы (2)), синхронизация колебаний (рис. 1а) наступает через 1125 периодов для первого сообщества и 900 периодов для второго. На языке нелинейной динамики говорят о различной длине переходного процесса к устойчивому синхронному состоянию. С течением времени моментальные значения численности и фазы колебаний сближаются и разность фаз стремится к нулю, при этом разность моментальных амплитуц через указанный промежуток времени падает до нуля (рис. 16). Возникает полная взаимная синхронизация колебаний, то есть рас сматриваемые сообщества в равной степени воздействуют друг на друга и взаимно подстраивают свои ритмы.

При указанном значении параметра связи (Ь =0,005), после некоторого переходного процесса, в системе устанавливаются стационарные колебания численности, соответствующие движению фазовой точки вдоль предельного цикла (рис. 2а). Форма фазовой кривой а, следовательно, и вид колебаний полностью определяется внутренними параметрами системы. Эта кривая притягивает фазовые траектории: значения системы на двумерных проекциях фазового портрета обоих сообществ, начиная с указанного момента времени совпадают, что также указывает на полную синхронизацию. Крестиками на рис. 2а обозначены начальное состояние системы, жирными точками - состояния в рассматриваемый момент времени. Стрелками указано направление движения по фазовой кривой.

Из рис. 26 видно, что из асинхронного режима развитие сообществ переходит в квазипериодический, затем колебания через указанный промежуток времени начинают синхронизироваться. Графики приближаются и сливаются с прямой, которая является биссектрисой угла и соответствует полной синхронизации колебаний.

С увеличением значения параметра связи (относительной доли миграции 6) синхронизация наступает на-

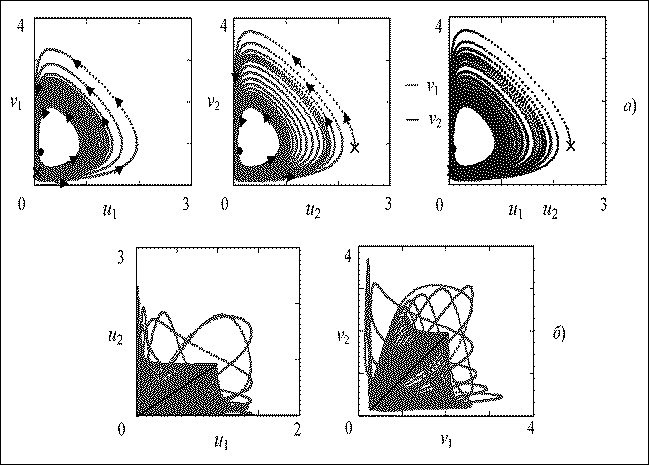
Рис. 2. Двумерные проекции траекторий системы (2) при Ь=0,005

много раньше. Так приа=0,3 и/>=0,05 полная взаимная синхронизация колебаний наблюдается через десять периодов для обоих сообществ (моментальные значения численности совпадают, разность моментальных ампли-туц падает до нуля).

Очень сильная миграционная связь стремится сделать состояния обоих осцилляторов идентичными максимально быстро. Численно установлено, что в процессе увеличения относительной доли миграции выделяется предельное значение Ъ«Ю,2, при переходе через которое количество периодов до достижения полной синхронизации не увеличивается. В этом случае полная взаимная синхронизация колебаний наблюдается уже на третьем периоде колебаний, и рост параметра связи не сокращает и не увеличивает это время.

Заключение

Представленная в работе простейшая модель динамики взаимосвязанных сообществ описывает изменение во времени общей численности видов при условии, что все особи считаются идентичными, а величина численности является основной характеристикой популяции. Такое сравнительно простое описание, в котором разнообразие свойств особей не учитывается, позволяет построить и исследовать модель, отражающую динамику взаимодействия соседних сообществ, провести качественное описание поведения модели, определить условия синхронизации колебаний численности рассматриваемых сообществ, изучить влияние миграционного взаимодействия между сообществами на динамику каждой популяции.

В результате исследования показано, что введение коэффициента миграции в классическую модель Лотки-Вольтерра или «хищник-жертва», приводит к синхронизации колебаний рассматриваемых систем. При этом происходит как захват периода колебаний, так амплитуды и фазы. Величина коэффициента миграции непосредственно влияет на скорость достижения полной синхронизации. Показано, что при малой интенсивности миграций для достижения полной синхронизации каждому сообществу может потребоваться разное число популяционных циклов, что связано с первоначальным различием в периодах колебаний изолированных систем.

Рассмотренная модель может быть использована далее для решения прикладных задач, связанных с управлением численностью эксплуатируемых популяций.

Исследование проведено при частичной финансовой поддержке комплексной программы фундаментальных исследований Дальневосточного отделения РАН(42П).