Условное среднее значение очередей в системах массового обслуживания, с пакетными потоками заявок

Любой пакетный трафик мультисервисных сетей связи является продуктом компьютерной обработки, выполняемой процессором при решении задач приложений. Решение каждой такой задачи состоит из трех последовательных этапов: получение исходных данных, процесс обработки и процесс выдачи результатов, причем трафик образуется именно на третьем этапе. Это и обусловливает его пачечный характер. Пакеты группируются в «пачки» в одних промежутках времени и практически отсутствуют в других промежутках [1].

Случайный процесс поступления заявок (пакетов) в систему характеризуется законом распределения, устанавливающим связь между значениями случайной величины и вероятностями появления указанных значений. В большинстве случаев такой поток характеризуется функцией распределения временных интервалов между соседними заявками. Имеется также множество работ, в которых потоки заявок характеризуются функцией распределения числа заявок за условную единицу времени.

В предыдущих работах [3-6] в качестве указанной единицы времени рассматривался по стоянный интервал времени т обработки одной заявки. Было показано, что дисперсия и корреляционные свойства числа заявок, поступающих за интервал обработки, оказывают определяющее влияние на средний размер очереди. Для одноприборной системы массового обслуживания (СМО) на основании рекуррентного соотношения (1), где HL (г) и qA^ – числа заявок, поступивших в течение i-го интервала т , и размер очереди, образовавшейся на указанном интервале, соответственно,

Qi (^г) - Qi-\ (^г) + ^mi (^т) ^- ^/ (^т\      (1)

ВД =

О, если q_i-x (г) = тДг) = 0;

1 в противном случае.

Была установлена связь между средними размерами очередей q{p) и параметром загрузки р вида q^ = ^\. (2) 2(1-/?)

где Е_т<Р^ = D_m<р^ + lCo_VqMllli (р) - р(1 - р);

D_m {р} – дисперсия чисел заявок на интервалах обслужив ания т , а также

^C°^V_qi__xm, <Р^ = [^,-1 (^) * ^(/^)] ' ["^г, (Р) * РА – второй взаимный центральный момент указанных последовательностей, называемый корреляционным моментом, или ковариацией. Он определяется как математическое ожидание произведений центрированных значений элементов q_i-x (г) и m_i (т). Соотношение (2) обобщает формулу Хинчина-Поллячека [2; 7-10] и справедливо для любых стационарных и ординарных потоков заявок при по стоянном времени обслуживания т . Для пуассоновского потока ^Е,М = р , и формула (2) приобретает обычный вид: q(p) = p /2(1-/?).

Применение указанной формулы для расчета очередей пачечных потоков приводит к по-грешно стям, превышающим сотни процентов. На рис. 1 представлены числа пакетов, по ступающих в течение интервала т (черные линии) и пуассоновского потока (серые линии), при одинаковой загрузке Р-^Х.

Видеотрафик по сравнению с пуассоновским обладает существенной неравномерностью и носит пачечный характер, что приводит к возникновению больших очередей.

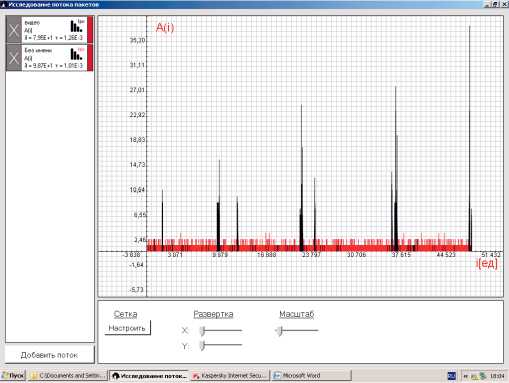
Рис. 1. Числа пакетов видеотрафика, поступающих в течение интервала т (черные линии) и пуассоновского потока (серые линии)

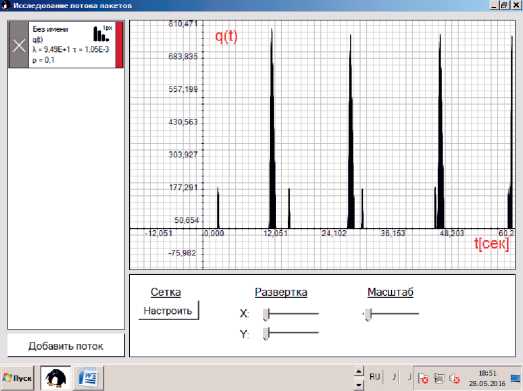
Рис. 2. График изменения мгновенных значений размеров очередей для видеотрафика

На рис. 2 показан график изменения размеров очередей для рассмотренного выше видеотрафика. Пиковые значения размеров очередей достигают 800 заявок (пакетов), в то время как для пуассоновского потока они не превышают пяти заявок.

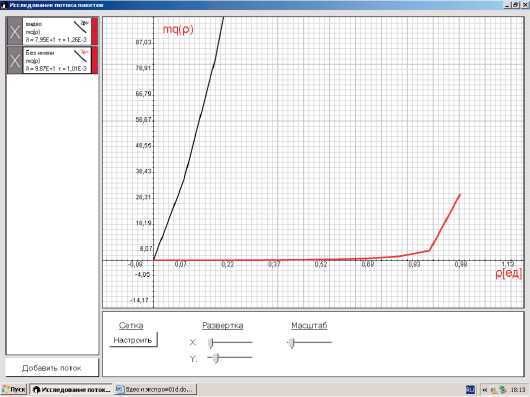
Рис. 3. Зависимости средних значений размеров очередей от изменения коэффициента загрузки р

На рис. 3 показаны зави сим ости средних значений размеров очередей qlp) от изменения коэффициента загрузки р для рассматриваемого видеотрафика и пуассоновского потока. Размеры очередей для пуассоновского потока несравнимо меньше, чем для потока видеотрафика. Поэтому для анализа видеотрафика следует применять обобщенную формулу (2).

Очереди при малых загрузках

Размеры очередей в коммутаторах мульти-сервисных сетей определяют объемы буферной памяти, требуемой для их хранения, и размеры задержек пакетов в процессе их обработки. Для обеспечения допустимых значений указанных параметров необходимо соответствующим образом уменьшать загрузку. Поэтому особый интерес представляет анализ характеристик трафика при малых значениях коэффициента загрузки р .

На рис. 4 для рассмотренного выше потока ви деот рафика показан график изменения функции qVp^ при значениях коэффициента загрузки, не превышающих Р = од. Из графика видно, что при малых загрузках можно выделить три интервала изменения характеристики. На начальном участке, до некоторого значения р ₀, значения q

равны нулю. На промежуточном участке происходит нелинейное возрастание характеристики.

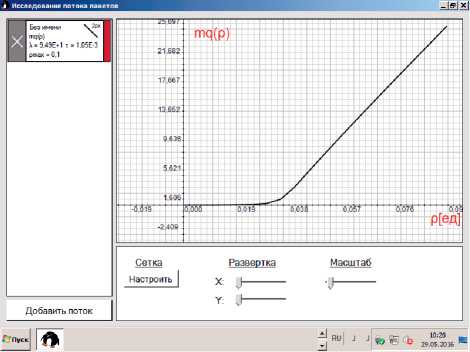
Рис. 4. График изменения q^p^ для потока видеотрафика при р <0,1

Далее характеристика изменяется почти линейно. Появление начального участка характеристики объясняется тем, что на этом интервале изменения коэффициента загрузки интервал времени обработки всегда остается меньше, чем минимальный промежуток времени ^min между двумя соседними заявками, и в интервал т не мо- жет попасть более одной заявки. Дисперсия при этом определяется как D,M = P^-P\Под-ставляя это значение в (2), получим q(p) = 0, что и следовало ожидать.

Введем поняти е усл ов ного среднего значения размера очереди Q(p) = q(pPp, которое представляет среднее значение очереди на каждом из интервалов г , при условии активной загрузки процессора, и не учитывает наличия интервалов простоя. Из графика рис. 4 следует, что коэффициент загрузки р = 0,03 приблизитель но с оответствует средн ему значению очереди q

= 1 • При этом №) = 33 заявки, что в 33 раза превышает среднее значение очереди qlpv Таким образом, среднее значение qVp^ не отражает реальное состояние очередей и для характеристики размеров очередей следует ориентирова ться на условные средние значения чисел заявок Q(p) •

Аппроксимация

Для получения значений коэффициента загрузки р , обеспечивающих допустимые размеры очередей, особый интерес представляет функция p^qY обратная представленной на рис. 4. Пр ед лагается аппроксимировать зависимость pVq^ функцией

P p₀ > 0 , (3)

где q – максимально допустимое значение среднего размера очереди; P^ = P – максимально допустимое значение коэффициента загрузки; р_й, а и b – постоянные коэффициенты, определяемые в процессе аппроксимации.

Зависимость P^- показанная на рис. 4, представляет обратную функцию i Г I-------------------------12

^ = L ^T^ -l при p > _Po;

4(/-            b- q{p} = b при p

Предлагается следующий алгоритм аппроксимации.

• 1.    Устанавливается предельное значение изменения коэффициента загрузки Pmax '

• 2.    Определяется шаг дискретизации по p, равный ^p = 0,05p_inax.

• 3.    Путем перебора находится значение минимального интервала между двумя соседними заявками ^min "

  4. Определяется значение

  
  

  2^^ kp

  
  

  где

  
  

  Np

  
  

  – округление до ближайшего цело-

• го числа начиная с нуля.

• 5.    По имеющейся характеристике опреде-

• ляется предельное значение размера очереди q

• 6.    Определяется предельное значение коэффициента ^max ,    , *

• 7.    Определяется предельное значение коэф-

• 1              — Ртах Po

• 8.    Определяется шаг дискретизации по (2 и по b, равные ^{Ati = 0},⁰Kax и Nb = O£\b_, соответственно.

• 9.    Начальное состояние: p = p₀, a = 0, b = 0 .

• 10.    Производится приращение p = p₀+Np.

• 11.    Производится приращение a = a + Na .

• 12.    По формуле (2) определяется значение qkp-pY и сравнивается с текущим значением q(p) ■

• 13.    Если q то приращение Na вычитается из a.

• 14.    Производится приращение b = b + Nb.

• 15.    По формуле (2) определяется значение q^p-p^ и сравнивается с текущим значением q(p) •                   ____

• 16.    Если q(p-p₀)^q то приращение Nb вычитается из b.

• 17.    Если в обоих пунктах 13 и 16 вычитания не произошло, то пункты 11-16 повторяются, пока хотя бы в одном из пунктов 13 или 16 произойдет вычитание.

• 18.    Пункты 10-17 повторяются, пока значение p достигнет значения Pmax *

• 19.    Окончательные значения коэффициентов a, b и p₀ являются искомыми для уравнения аппроксимации (3).

^Amax)

фициента ^max -------2 '

Коэффициент b может иметь отрицательное значение, в то время как коэффициент а всегда положителен. Следует заметить, что коэффициент Po определяется сразу и не меняется, в процессе аппроксимации Po ^ ^min '

Для рассмотренного выше видеотрафика были получены следующие значения параметров аппроксимации: p₀= 0,025; a =0,0024; b = 0,0019. Интенсивность трафика 2 = 79,5 пак/с .

Задержки в очередях

Учитывая, что q = Ж, где W – допустимое среднее время задержки в очереди, получим

p(AW) = p₀+ aAW + Ьл[ж , где Р = Р(ЛЮ – максимально допустимое значение коэффициента загрузки, обеспечивающее допустимое среднее время задержки в очереди W.

Полагая допустимое среднее время задержки в очередях коммутаторов fF = 30 мс, для рассмотренного выше видеотрафика получим максимально допустимое значение коэффициента загрузки p, = 0,033. Максимально допустимое значение среднего размера очереди q = 79,5 пак/с-0,03с = 2,38 пак. При этом условное среднее значение размера очереди g = -^ = ^^- = 72,12 пакета, а среднепиковое

P; 0,033

значение, превышающее его в два раза, составляет 39,6 пакета.

Следовательно, при выборе размеров буферной памяти, как мы уже показали, необходимо ориентироваться на условные средние значения размеров очередей Q- При этом размер памяти, требуемой для буферизации очереди, следует выбирать с двойным запасом, поскольку среднепиковые значения очередей почти вдвое превышают условные средние значения.

Для каждого конкретного кодека типа i полоса пропускания определяется соотношением fki = ^i^Ls, ’ ^{ГДе L}xi – длина полезной части информации для кадра трафика. В результате получим

w

Pi = Po. + ^ai — fk. + b, • (4)

Полагая длину полезной части информации для кадра трафика Zs; = 1 Кбайт = 8000 бит, определим полосу пропускания для рассматриваемого видеокодека:

f_ki = 79,5 пак/с • 8000 бит/пак = 640 Кбит/с .

В этом случае пропускная способность Fj порта коммутатора, к которому подключается пользователь услуги, должна быть не менее

F.-

640 Кбит/с .. .       ,

-----------= 19,4 Мбит/с •

0,033

Заключение

Предлагаемые интервальные методы позволяют обобщить формулу Хинчина-Поллячека и при заданном коэффициенте загрузки охарактеризовать трафик любого приложения с помощью двух параметров, непосредственно связанных с размерами очередей и задержек, которые возникают в СМО с заданной пропускной способ- ностью. Показано, что средние значения q(p) не отражают реальное состояние очередей и при выборе размеров буферной памяти следует ориентироваться на условные средние значения чисел заявок Q(p) • Именно условные средние значения определяют пропускную способность порта коммутатора. Несмотря на то что полоса пропускания для рассматриваемого кодека составляла 640 Кбит/с, пропускную способность порта коммутатора, к которому подключается пользователь услуги, следует выбирать не менее 19 Мбит/с. В противном случае будут наблюдаться временные задержки, превышающие допустимые значения.