Условные морфологические меры сложности и информативности изображений

В морфологии Пытьева [1] понятие «морфологической сложности» мозаичной формы изображения традиционно вводится следующим образом.

Пусть изображение представляет собой непрерывно определенную двумерную функцию распределения яркости на кадре

f ( x , y ): О > R , fie R 2 ,                         (1)

где О - область кадра ограниченного размера, R -множество действительных чисел, R ² – плоскость кадра. Кадр будем считать прямоугольным, хотя в общем случае форма кадра может быть произвольной. Такие изображения являются элементами гильбертова пространства L ²( О ) со скалярным произведением ( f , g ), нормой || f || и евклидовым расстоянием d E ( f , g )=|| f –g||.

Пусть теперь мозаичное изображение представляет собой кусочно-постоянную функцию вида

f ⁽ x,У ⁾ = £ _{i — 1 n} f X _F ⁽ x, У ⁾ ,                       (2)

где n - число областей разбиения F кадра О на связные непересекающиеся области постоянной яркости, F = { F 1 , ..., F n }, f =( f 1 , ..., f n ) – вектор действительных значений яркости, соответствующих каждой области разбиения; х _Fi ( x , у ) е {0,1} - характеристическая функция i -й области яркости:

[ 1,( x , у ) е F ,

X _п ( x , У ) = L,                               (3)

[ 0,( x , у ) g F i .

Множество изображений одной формы разбиения кадра F в таком случае образовывает выпуклое и замкнутое подпространство F ^ L2(0):

F = { f ( x , У ) = L-! n-fi X Fil x , У ), f е R ⁿ }. (4) — 1... n

В рамках данной работы мы будем говорить о пыть-евских разбиениях кадра как о мозаичных формах. Легко убедиться, что пытьевские формы образуют алгебраическую структуру типа «решетка», в которой для любых двух форм F и G можно указать форму более сложную F л G и менее сложную F v G . Более сложные формы получаются из менее сложных разбиением, а менее сложные из более сложных – слиянием областей. Форма F л G содержит набор областей, образующихся попарным пересечением исходных форм F и G . Форма F v G - это такая форма, которая является наиболее сложной среди всех форм, являющихся более простыми как по отношению к F , так и по отношению к G . При этом образуется множество монотонно вложенных друг в друга пытьевских форм (классов изображений), получаемых последовательным разбиением исходной формы (или, напротив, последовательным слиянием областей базовой формы).

Как видно, введенное таким образом отношение «более сложный по форме» (записывается F> G о F=Fл G о F ^ G) является отношением не полного, а частичного порядка – большинство форм являются несравнимыми по сложности. В связи с этим в работе [10] был предложен способ распространения морфологического отношения «более сложный по форме» на множество всех пытьевских форм, причем формируется не только бинарное отношение, но и мера сложности. Мерой сложности образа было предложено называть любую такую неотрицательную функцию от некоторого дескриптора формы образа, которая монотонно увеличивается при таких последовательных трансформациях образа, при которых число его элементов увеличивается. В частности, ранее было показано, что для мозаичных форм изображений, описываемых разбиением F кадра Q площади S на непересекающиеся связные области Fi с соответствующими площадями Si, подобной мерой сложности является:

n цн (F) = S Pi' (1 - Pi) = i =1

n

Е 2 S

Pi, Pi = —, I = 1... n .

= 1               S

нее рассматривавшийся лишь в рамках математических морфологий типа Серра [2]. Карты толщин ранее были рассмотрены, в частности, в работе [3], где они использовались в качестве вспомогательного инструмента для построения морфологических спектров, впервые предложенных Марагосом [4] и затем обобщенных в работе [5].

Заметим, что количество информации по Шеннону (информативность)

I ⁽ F ) =- E Pi' log Pi

также является мерой сложности мозаичной формы в указанном смысле.

Такое определение мер сложности и информативности полностью согласовано с морфологией Пытьева, однако не вполне согласовано с интуитивным представлением о сложности мозаичных форм, поскольку эти функции зависят лишь от площадей областей мозаичной формы, но не от формы областей, которая также может быть более или менее сложной. Рассмотрим простые примеры мозаичных форм на дискретном кадре размера 6×6, показанные на рис. 1. Дискретные изображения будем рассматривать как частный случай непрерывных, таких, что каждому пикселу дискретного изображения соответствует квадратная область единичного размера на непрерывном изображении. Заметим, что интуитивно кажется, что форма A , содержащая 2 области равной площади, существенно проще не только по сравнению с формой В , содержащей больше областей меньшей площади, но и по сравнению с формой Б , содержащей такое же количество областей той же площади, что и A (2 области площадью полкадра). При этом впечатление большей сложности формы Б возникает, очевидно, не за счет изменения количества или различий в размерах (площади) областей, а за счет их сложной формы: визуально форма Б , состоящая из узких полос, ближе по сложности к форме В , также состоящей из узких полос, чем к форме A , состоящей из широких полос. Этот простой пример показывает, что учет только распределения площадей областей разбиения недоста-

1. Условные меры сложности и информативности

Пусть задан некий набор структурирующих элементов (связных бинарных фигур, СЭ) B , упорядоченных по размеру (площади), которые называются множеством элементов покрытия. Тогда картой толщин бинарной фигуры H относительно B называется такая функция т H , B ( x , у ), которая каждой точке фигуры ставит в соответствие площадь максимального покрывающего ее элемента из B , целиком вписанного в фигуру H . Соответственно, картой толщин мозаичной формы F = { F 1 ... F n } относительно B называется такая функция т _F , B ( x , у ), которая каждой точке кадра ( x , у ) ставит в соответствие площадь максимального покрывающего ее элемента из B , целиком вписанного в ее область принадлежности:

т F , B ( X , У ) = Т F i , B ( x , у ): ( x , у ) € F i .

Используя мозаичную модель формы, карту толщин можно описать как т fb (x, У) = S    т fb(x, У) X F (x, У).             (7)

,                               = 1.. n ,

Введем понятие аморфных СЭ. Пусть аморфный СЭ с центром в некоторой точке кадра целиком заполняет связную область F_i мозаичной формы F , которой принадлежит эта точка (т.е. принимает форму и размер этой области F_i ). Легко убедиться, что в случае, когда B представляет собой множество A аморфных СЭ, т _F , A ( x , у ) = S i , если ( x, у ) е F i . Отсюда:

JJ_fi ^T f , a ^{( x} , у ^)d x ^d у = S n = 1 Si² = S 2 ' ^{(1 -}Ц н ^{( F} )) ^

^ ц _H ( F ) = 1 - mean _n

^mean _fi ⁽ f ^{( x} , у ))

( ^т fa ^{( x} , у ) )

I S J,

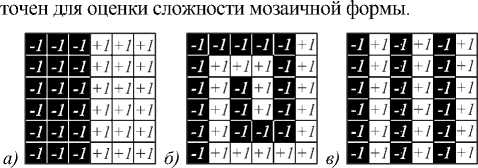
Рис. 1. Примеры мозаичных форм различной сложности: 2 области простой формы (а); 2 области сложной формы («спираль») (б); 6 простых областей, схожих с формой «спираль» (в)

Чтобы преодолеть этот недостаток, в данной работе предлагается объединить аппарат мозаичных моделей формы Пытьева с аппаратом карт толщин, ра-

JJ_fi f ^{( x} , у ^)d x ^d у [f , ^{1d x d у}

т.е. введенная ранее мера сложности ц _н ( F ) может интерпретироваться как средняя нормированная площадь максимальной покрывающей фигуры из множества A аморфных СЭ. Обобщая эту идею, условной морфологической сложностью ц _н , B ( F ) мозаичной формы F относительно заданного набора структурирующих элементов B , предлагается называть функцию

Ц н , B ^{( F} )

1 - mean _n

( ^т f , b ^{( x} , у ) )

.

I S )

Для того, чтобы качественно оценить свойства введенной функции морфологической сложности, рассмотрим формы с рис. 1. Соответствующие им

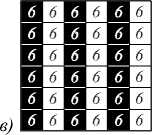
прямоугольные карты толщин (здесь B – множество всех прямоугольников) показаны на рис. 2. Как видно, карта прямоугольных толщин для формы B оказалась строго меньше не только карты толщин для формы A , но и даже карты толщин для формы В , а значит, ц H, _в ( Б) >  ц H, _в ( В )> ц H, _в ( A ). Интуитивно это понятно – в форме B есть не только вертикальные, но и горизонтальные области, а также углы, отрезки разной длины, т.е. она разнообразнее, а значит, сложнее. Таким образом, мы убедились, что на качественном уровне введенное понятие морфологической сложности форм вполне соответствует интуитивным представлениям человека.

а)

18	18	18	18	18	18
18	18	18	18	18	18
18	18	18	18	18	18
18	18	18	18	18	18
18	18	18	18	18	18
18	18	18	18	18	18

б)

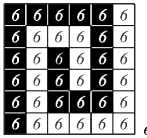
Рис. 2. Карты толщин, соответствующие формам с рис. 1

Важным частным случаем такой условной меры сложности является случай, когда B = D – множество дисковых структурирующих элементов произвольного размера. В этом случае мера сложности мозаичной формы будет инвариантна к повороту и масштабированию изображения. Кроме того, такая карта толщин, а значит, и мера сложности может быть быстро вычислена при помощи непрерывного скелета [3]. В других случаях могут применяться другие наборы СЭ, например, эллиптические, прямоугольные и т.п. При этом будут получаться различные меры условной сложности, характеризующие не только распределение размеров, но и распределение локальных форм мозаичных областей.

Аналогично легко заметить, что:

I ⁽ F ) = ^- Е Р.' log Р - =

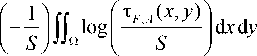
Откуда

I A ⁽ F ) = ^- mean n

log

Г ^T F , A ⁽ x , У ) ) l ^ J

Соответственно, условной морфологической информативностью I B ( F ) мозаичной формы F относительно заданного набора структурирующих элементов B предлагается называть минус средний логарифм нормированной площади максимального покрывающего СЭ из данного множества:

I B ^{( F} ) = - mean n

log

( ^T F , B ⁽ x , У ) ) l ^ j

Такая условная информативность характеризует распределение информации не только по размерам, но и по формам локальных областей мозаичной формы.

Необходимо отметить, что предложенные обобщения мер сложности и информативности будут являться полностью корректными лишь в тех случаях, когда они удовлетворяют введенному ранее условию: они должны монотонно увеличиваться при таких последовательных трансформациях образа, при которых число его элементов увеличивается. Для мозаичных форм это означает, что при любом разбиении любой области мозаичной формы на две подобласти введенные функции ц H, _B(F) и I_b( F) должны увеличиваться (отсюда автоматически следует, что при любом слиянии двух соседних областей формы в одну эти функции должны уменьшаться). В исходных выражениях (т.е. при B = A , для множества аморфных СЭ) выполнение этого условия очевидно, т.к. при разбиении любой области мозаичного покрытия на две части средний размер области строго уменьшается. Однако обобщенные выражения монотонно зависят от, вообще говоря, произвольной функции т _F , _в(x,у ), и, следовательно, их свойства зависят от свойств данной функции, а именно: функции ц H, _в ( F) и I B ( F) увеличиваются, если τ F , B ( x , y ) убывает, и убывают, если τ F , B ( x , y ) возрастает. В связи с этим исследуем поведение карты толщин при разбиении областей мозаичной формы.

Докажем сначала более слабое свойство.

Утверждение 1. При любом заданном множестве структурирующих элементов B , карта толщин мозаичной формы F не возрастает при разбиении областей формы: F > G ^ т f , в ( x,у ) <  т g ,в ( x,у ).

Доказательство. Фиксируем некоторую точку ( x , y ) и рассмотрим множества всех покрывающих ее элементов из B , целиком вписанных в ее область принадлежности в формах F и G соответственно. Поскольку область принадлежности любой точки в более сложной (по Пытьеву) форме F всегда целиком принадлежит области принадлежности в менее сложной форме G , то, соответственно, и множество вписанных СЭ такой области из F целиком принадлежит множеству вписанных СЭ содержащей ее области из G . Отсюда следует, что ни одного нового вписанного СЭ, покрывающего рассматриваемую точку в F по сравнению с G, появиться не может. А, значит, при переходе от G к F максимальный размер покрывающего СЭ в данной точке не может увеличиться, поскольку в F не появится новый максимальный покрывающий вписанный СЭ, больший, чем в G . Поскольку такое рассуждение справедливо для всех точек карты толщин, можно заключить, что при любых последовательных разбиениях мозаичной формы значения карты толщин монотонно не возрастают.

Отсюда следует, что справедливо следующее утверждение:

Следствие 1. При любом заданном множестве структурирующих элементов B, функции ц H, _в ( F ) и I B ( F ) не убывают при разбиении областей мозаичной формы: F > G ^ ц н,в ( F ) >  ц н , в ( G ), I b ( F) > I b ( G ).

Однако для точного соответствия ранее введенным определениям этого недостаточно. Необходимо, чтобы эти функции строго возрастали при разбиениях областей формы, а для этого необходимо, чтобы и карты толщин удовлетворяли следующему более сильному свойству - они должны строго убывать при разбиениях кадра:

( F >  G : F >  G , F * G ) ^

>^т F , в ⁽ x , У ) <^т G , в ⁽ x , У ) °

° ^{V (} x , y ): ^т F , в ⁽ x , У ) < ^т G , в ⁽ x , У );

^{3 (} x , У ^{): т} F , в ⁽ x , У ) <^т G , в ⁽ x , У ).

К сожалению, для СЭ произвольной формы это условие не выполняется. Рис. 1 демонстрирует пример разбиения фигуры (области) прямоугольной формы, при котором размер максимального покрывающего элемента квадратной формы остается неизменным. Как показано на рис. 3 вверху, можно указать такие точки исходной области (фигуры), для которых разрез пересекает максимальные покрывающие СЭ. Однако, как показано на рис. 3 ниже, при этом все равно можно найти другие покрывающие СЭ того же размера, что и прежний максимальный СЭ, не затронутые разрезом. Нижний рисунок на рис. 3 показывает, что в данном случае вся карта толщин после разреза останется неизменной, поскольку вновь образовавшиеся области можно целиком покрыть объединением оставшихся прежних максимальных СЭ, не затронутых разрезом (не пересекающихся с линией разреза).

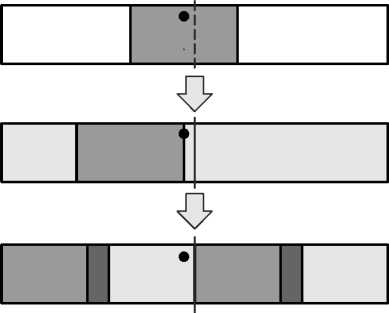
Рис. 3. Пример разбиения фигуры (области) прямоугольной формы, при котором размер максимального покрывающего элемента квадратной формы остается неизменным во всех точках кадра

Однако, как показано на рис. 4, в случае строго выпуклых, в частности, дисковых СЭ, ситуация меняется (строго выпуклые фигуры - это такие выпуклые фигуры, границы которых не содержат прямолинейных отрезков). Теперь можно указать точки, в которых после разреза более не существует ни одного покрывающего СЭ прежнего размера. На рис. 4 снизу темным показано объединение всех исходных максимальных СЭ, не затронутых разрезом - в этих точках значение карты толщин после разреза не меняется. Во всех остальных точках (помечены белым цветом) значение карты толщин после размера строго уменьшается, т.е. вся карта толщин как единая функция на кадре в данном примере строго убывает вследствие произведенного разреза.

Естественно, одного примера и общего качественного рассуждения недостаточно для доказательства желательного свойства дисковой карты толщин. Ниже приведено строгое доказательство этого утверждения.

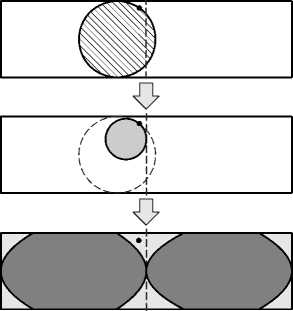
Рис. 4. Пример разбиения фигуры (области) прямоугольной формы, при котором размер максимального покрывающего элемента дисковой формы уменьшается (во всех точках, помеченных светлой областью на нижнем рисунке)

Утверждение 2. При использовании множества структурирующих элементов D дисковой формы дисковая карта толщин мозаичной формы F убывает при разбиении областей формы:

( F >  G : F >  G , F * G ) ^

>^Т F , D ⁽ x , У ) <^т G , D ⁽ x , У ) °

° ^{V (} x , У )^{: т} F , D ⁽ x , У ) < ^т G , D ⁽ x , У );

• ^{3    (} x , У ^{): т} f , d ⁽ x , У ) <^т g , d ⁽ x , У ).

Доказательство. Первая часть данного утверждения непосредственно следует из Утверждения 1:

F>G⇒F≥G⇒

^ ^{V (} x , У ) ^{: т} f , d ⁽ x , У ) < ^т g , d ⁽ x , У ) .

Для доказательства второй части утверждения необходимо показать, что существует хотя бы одна точка фигуры (области), в которой после разреза значение карты толщин уменьшится. Рассмотрим максимальный покрывающий диск, касающийся границы фигуры в некоторой точке контура P (рис. 3). Для любой невырожденной точки контура, где существует касательная к контуру, существует единственный максимальный вписанный круг, покрывающий данную точку контура. Это связано с тем, что множество всех вписанных дисков, покрывающих данную точку, представляет собой множество дисков, касающихся контура в данной точке, т.е. имеющих радиус, исходящий из этой точки и перпендикулярный касательной к контуру в этой точке. Назовем это семейство дисков касательными дисками для точки P. Все они упорядочены по размеру, и не существует двух касательных дисков одинакового размера. Максимальный из этих дисков касается границы фигуры как минимум еще в одной точке. Это единственный макси- мальный покрывающий диск для данной точки, поскольку все остальные касательные диски для этой точки меньше его по размеру.

Предположим, что произведен разрез фигуры, разделяющий ее на части и при этом разрезающий (пересекающий) максимальный касательный диск для точки P . В этом случае такой диск больше не может быть максимальным касательным диском для P , т.к. он не вписывается целиком в уменьшившуюся часть области (фигуры), содержащую P . Новым максимальным касательным диском для P станет такой касательный диск, который целиком содержится в новой области принадлежности точки P и при этом касается также линии разреза. Поскольку исключенный (разрезанный) диск был максимальным, а все остальные касательные диски были меньшего размера, то после разреза значение карты толщин в точке P уменьшится (рис. 5).

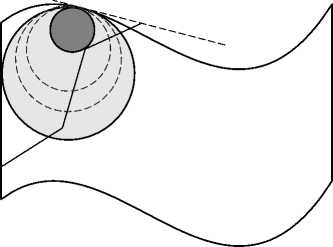
Рис. 5. Максимальный покрывающий диск (заливка), касающийся границы фигуры в заданной точке; касательная к контуру фигуры в данной точке; семейство покрывающих дисков, касающихся границы фигуры в заданной точке (пунктирные окружности); линия разреза фигуры, пересекающая максимальный покрывающий диск;

новый (меньший) максимальный покрывающий диск, касающийся границы фигуры в данной точке, а также касающийся линии разреза (темная заливка)

Но всегда ли можно утверждать, что при любом разрезе фигуры любой произвольной формы на ее контуре обнаружится такая точка P, максимальный касательный диск которой окажется разрезан? Да, это можно утверждать, поскольку существует конструктивный способ отыскать такую точку. Идея этого способа показана на рис. 6. Как известно, дисковым скелетом двумерной фигуры называется множество центров всех максимальных вписанных дисков. Доказано, что такой скелет всегда представляет собой плоский планарный граф, и существуют эффективные алгоритмы построения таких скелетов, в частности, для полигональных фигур произвольной формы [6]. После разреза скелет изменится. Теперь он будет состоять из объединения скелетов двух получившихся после разреза фигур. При этом часть прежних максимальных вписанных дисков в любом случае окажется разрезан, а их центры будут исключены из совокупного скелета разрезанной фигуры. Таким образом, достаточно построить дисковые скелеты фигуры (области) до и после разреза, а затем определить, какие точки скелета оказались из него исключены - так мы узнаем, какие мак- симальные вписанные диски перестали быть таковыми. Выберем любую такую исключенную точку исходного скелета и определим точки касания соответствующего максимального диска на контуре исходной фигуры. Это и есть искомая точка, в которой карта толщин после разреза строго уменьшается.

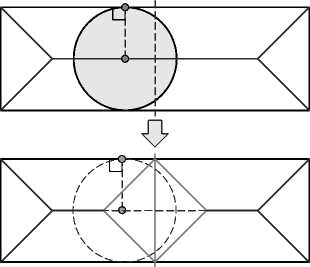
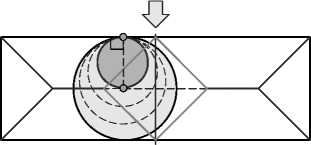
Рис. 6. Исходный дисковый скелет; измененный скелет после разреза; точка на удаленной после разреза части исходного скелета; проекция этой точки на контур исходной фигуры; семейство касательных дисков к точке-проекции; новый (уменьшенный) максимальный касательный диск

Таким образом, Утверждение 2 можно считать полностью доказанным.

Следствие 2. При использовании множества структурирующих элементов D дисковой формы функции ц H , D ( F) и I_D ( F ) возрастают при разбиении областей мозаичной формы:

F > G ^ ц н , d ( F ) >  ц н , d ( G ), I d ( F ) > I d ( G ).

На самом деле изложенное выше доказательство справедливо не только для дисковых, но и для любых строго выпуклых СЭ, для которых существуют касательные семейства вписанных СЭ и скелеты обладают схожими свойствами (обобщенным скелетом двумерной фигуры по множеству СЭ заданной формы называется множество центров всех максимальных вписанных СЭ этой формы). Выпуклые СЭ многоугольной формы не являются строго выпуклыми, т.к. допускают наличие нескольких различных максимальных вписанных касательных СЭ в точке контура фигуры. Именно этим объясняется сохранение неизменной карты толщин квадратных СЭ при разрезе прямоугольника (рис. 1). Однако на практике любой полигональный СЭ легко преобразуется в близкий по форме строго выпуклый СЭ путем замены всех линейных отрезков контура дугами окружностей малой положительной кривизны с теми же конечными точками. Поэтому в дальнейшем мы будем считать, что B является семейством (набором) строго выпуклых СЭ. Для таких наборов СЭ предложенные обобщения мер сложности и информативности полностью корректны.

• 2.    Эксперименты с условными мерами сложности и информативности

Для проведения численных экспериментов с предложенными мерами сложности и информативности были использованы карты толщин на основе дискового структурирующего элемента. Были рассчитаны условные меры сложности и информативности для бинарных объектов, входящих в базу изображений Kimia99 [11].

База Kimia99. Размеры изображения – 275×275 пикселей. Объекты крупные, занимают не менее 50 % изображения, располагаются в центре изображения. Изображения бинарные, то есть состоят из двух областей, которые условно можно назвать объектом и фоном. Мера сложности изображения представляет собой набор мер сложности для каждой из областей изображения. Следовательно, каждому изображению базы ставится в соответствие двумерный вектор признаков («вектор информативности»), включающий условную меру сложности (информативности) области объекта и области фона (в дальнейшем просто «объекта» и «фона»).

Условные меры сложности

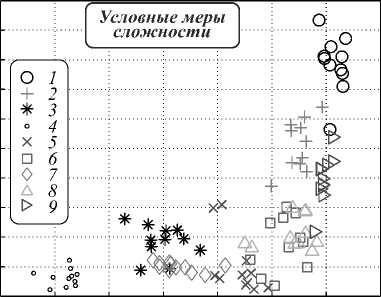
График распределения условных мер сложности по классам набора изображений приведён на рис. 7.

Условная мера сложности фона 0,85 0,80 0,75 0,70 0,65 0,60 0,55 0,50 0,45 0,40 0,35

0.4    0,5    0.6    0.7    0,8    0,9 1,0

Условная мера сложности объекта

Рис. 7. Распределение условных мер сложности изображений базы Kimia99 по классам. По горизонтальной оси отложена условная мера сложности объекта, а по вертикальной – фона

На рис. 7 видно, что объекты одного класса имеют схожие показатели мер сложности как для объекта, так и для фона. Отклонения объектов класса от центра класса в данном двумерном пространстве признаков представлены в табл. 1.

В табл. 2 более подробно представлены изображения двух классов из этой базы, расположенных по мере увеличения их сложности. Для каждого класса в таблице приведены изображение и длина собственного вектора данного изображения.

Как видно из приведенных выше таблиц и рис. 7, мера сложности объекта растет в связи с увеличением детализации объекта и уменьшается с уменьшением детализации соответственно. Также видно, что объекты класса «Животные», имеющие одинаковый биологический вид, обладают и близкими мерами сложности.

Табл. 1. Примеры отклонений объектов от центра класса

Эталонное изображение				1-е отклонение				2-е отклонение
			0,929 0,81				0,897 0,818				0,931 0,832
			0,856 0,845		^ц.		0,799 0,864				0,86 0,869
			0,603 0,865		ЧВ		0,529 0,864				0,668 0,852
	ф		0,426 0,841		ф		0,361 0,84		ф—		0,441 0,841
			0,753 0,871		тф		0,695 0,871		^		0,793 0,872
	к		0,827 0,882		>		0,76 0,88		X		0,858 0,901
	г		0,611 0,862		ф		0,581 0,864		г		0,714 0,861
			0,849 0,89				0,75 0,884				0,883 0,912
	к		0,893 0,895				0,878 0,876		X		0,912 0,904

Табл. 2. Примеры изображений объектов двух классов, отсортированных по мере увеличения их меры сложности

8-й класс «Животные»			6-й класс «Самолёт»
	^ 1	1,16	>	1,163
	^R	1,17	X УТ	1,179
	>	1,21	>^	1,189
		1,22	^у	1,194
		1,22		1,203
		1,23		1,209
	*fl 1	1,23		1,224
	и 1	1,24		1,226
		1,24	1 V 1	1,236
	>5?	1,26		1,244
	X 1	1,27		1,244

Аналогично мерам сложности приведены график и таблицы с результатами для мер информативности. График распределения условных мер сложности по классам набора изображений приведён на рис. 8.

Условная мера информативности фона

Условные меры информативности

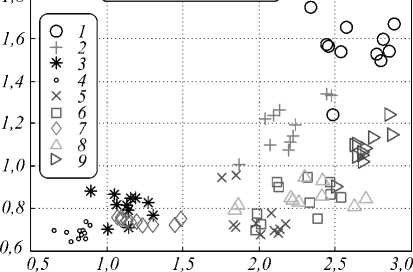
Условная мера информативности объекта

Рис. 8. Распределение условных мер информативности изображений базы Kimia99 по классам. По горизонтальной оси отложена условная мера информативности объекта, а по вертикальной – фона

Условные меры информативности

В табл. 3 приведены изображения двух классов из этой базы, расположенных по мере увеличения их информативности.

Табл. 3. Примеры условных мер информативности объектов

Наибольшая информативность				Наименьшая информативность
	У **		2,335 1,978		***х^		2,889 1,955
			1,869 2,109				2,475 2,227
	я®		0,891 2,042		4®		1,271 2,119
	ф		0,65 1,936		ф—		0,864 1,955
			1,757 2,178				2,174 2,19
	X		1,988 2,233				2,54 2,438
	f		1,091 2,037		г		1,486 2,056
			1,845 2,232				2,701 2,535
	л		2,501 2,236				2,87 2,442

В табл. 4 приведены примеры изображений с наибольшими и наименьшими показателями условной меры информативности. В качестве показателя условной меры считалась длина условного вектора, проведённого из начала координат в точку пространства, характеризуемую координатами – составляющими вектора информативности.

Табл. 4. Примеры изображений объектов двух классов, отсортированных по мере увеличения их меры сложности

6-й класс «Самолёт»		8-й класс «Животные»
X	2,990	1 ^ 1	2,896
1 * 1	3,022	1 ^ 1	2,938
	3,053	>	3,156
-Л?	3,084	1^1	3,185
	3,106	г*	3,221
^1^	3,267		3,248
х'	3,347	1 *” 1	3,305
Л^	3,367	1^1	3,360
	3,415	I'nl	3,363
	3,443		3,626
1	3,521	*	3,704

Как видно из приведенных выше таблиц и рис. 8, мера информативности объекта растет в связи с увеличением детализации объекта и уменьшается с уменьшением детализации соответственно. В отличие от меры сложности самолёты, хвост которых перекрыт прямоугольником, в большинстве случаев имеют меньшую информативность, чем их неперекрытые изображения. Также видно, что объекты класса «Животные», имеющие одинаковый биологический вид, обладают и близкими мерами информативности.

По рис. 8 можно определить, что объекты одного класса, то есть имеющие схожую форму, могут иметь разные меры информативности, и объекты разной формы могу иметь схожие значения информативности.

Также на меру информативности влияет искривление деталей на объекте, повышение детализации объекта или же, наоборот, отсутствие каких-нибудь частей объекта. Как видно из табл. 2, именно такие объекты обладают наибольшими и наименьшими показателями информативности в своём классе.

Заключение

В данной статье были введены понятия условной морфологической сложности и условной морфологи- ческой информативности определяемых относительно заданных наборов структурирующих элементов некоторой формы и вычисляемых с использованием соответствующих морфологических карт толщин. Исследованы математические свойства морфологических карт толщин и соответствующих им оценок морфологической сложности и информативности в зависимости от свойств используемых наборов структурирующих элементов.

Проведенные на открытой базе изображений Kimia99 эксперименты подтвердили, что предложенные оценки морфологической информативности действительно характеризуют степень детализации объекта: чем выше детализация, тем больше значение информативности. Как правило, изображения объектов одного типа имеют схожие показатели сложности и информативности. При этом, естественно, объекты различной формы могут иметь схожие показатели – мера информативности не является дескриптором формы, а лишь оценкой ее сложности.

Исследование выполнено за счёт гранта Российского научного фонда (проект № 16-11-00082).