Усовершенствование модели дистанционного контроля роста новопосаженных растительных плантаций

С точки зрения медицины исследование свойств воды необходимо проводить, опираясь не только на результаты стандартного анализа физико-химических параметров, но и с учетом биологических свойств воды и водных растворов. Последние достижения в области теоретической и экспериментальной физики подтверждают важность исследования свойств воды с точки зрения влияния ее структурных особенностей на биологические процессы в живых организмах.

При этом ключевую роль в процессе формирования тех или иных биологических свойств воды играют процессы, которые не могут быть описаны известными классическими физико-химическими моделями, а тре- буют привлечения новых подходов и методов. Большое значение в этом контексте уделяется изучению свойств воды с точки зрения квантовой электродинамики, поскольку было установлено, что биологические свойства воды в макро- и нано- масштабах имеют принципиальное отличие.

Изучение биологических свойств воды в рамках теории квантовой электродинамики привело к формированию новых моделей строения структуры воды как совокупности когерентных доменов. В аспекте эффективности протекания химических реакций и обмена веществ в биологических системах важную роль играют процессы взаимодействия между когерентными доменами межклеточной жидкости. В связи с этим особую актуальность приобретает разработка новых экспериментальных методов исследования квантовых свойств воды. Одним из таких методов является регистрация на сенсорном материале (рентгеновской фотопленке) изображений газоразрядного излучения жидкофазных объектов в электромагнитном поле – эффект Кирлиан.

При размещении исследуемого образца жидкости между двумя пластинами-электродами, на которые подается короткий импульс высокого напряжения, возникает электрический ток. Для протекания электрического тока необходимо наличие свободных носителей заряда, например, электронов. Получение части электронов происходит за счет процессов ионизации газового промежутка между образцом и электродом, друга часть электронов, участвующих в протекании электрического тока, индуцируется из жидкости.

Для воды с высокой степенью когерентности характерно присутствие большого количества квазисвободных электронов, которые при небольшом внешнем воздействии, легко покидают жидкость и участвуют в упорядоченном движении заряженных частиц. Благодаря этому эффекту зарегистрированные на сенсорном материале картины излучения для исследуемых образцов воды с большей или меньшей степенью когерентности отличаются. В ходе активного измерительного эксперимента образец исследуемого жидкофазного вещества выступает как источник излучения, мощность которого усиливается благодаря наведению внешнего электромагнитного поля. Анализ картины распространения лавинного и поверхностного разрядов проводится по интегральным и отдельным детализирующим показате-

Интегральным показателем степени когерентности образца может служить площадь засветки. Наименьшая площадь засветки характерна для дистиллированной воды. С точки зрения квантовой электродинамики, дистиллированная вода содержит в своем составе когерентные домены, но они не создают взаимной когерентности друг другом. Возрастание площади засветки по сравнению с дистиллированной наблюдается у образцов природной и воды из монастырских источников.

Для детализации анализа картины свечения используются также методы цифровой обработки изображений: спектральный и вейвлет анализ, фликкер-шумовая спектроскопия.

УСОВЕРШЕНСТВОВАНИЕ МОДЕЛИ

ДИСТАНЦИОННОГО КОНТРОЛЯ РОСТА НОВОПОСАЖЕННЫХ РАСТИТЕЛЬНЫХ ПЛАНТАЦИЙ

З.Г. Сафаралиев, Т.И. Сулейманов, Н.Г. Джавадов

Национальное аэрокосмическое агентство, г. Баку, Азербайджан

Как отмечается в работе [1], наиболее распро- страненными изменениями в земельном покрытии лесов после опустошающих пожаров являются: (а) зарастание кустарниками или молодыми стеблями; (б) насаждение лесных плантаций или использование в целях сельского хозяйства.

Для обнаружения изменений возникших в лесных массивах после пожаров в работе [1], предлагается использовать дифференцирование вегетационных индексов. При этом в качестве вегетационного индекса используется Атмосферно Защищенный Вегетационный Индекс ( ARVI ), определяемый как

ARVI =

NIR - RB

NIR + RB

где RB = R — у(B — R); NIR - сигнал на выходе ближ- него инфракрасного канала; R - красного канала; B -синего канала LANDSAT TM; у - коэффициент атмо- сферной коррекции, зависящий от оптической толщины атмосферы.

лям.

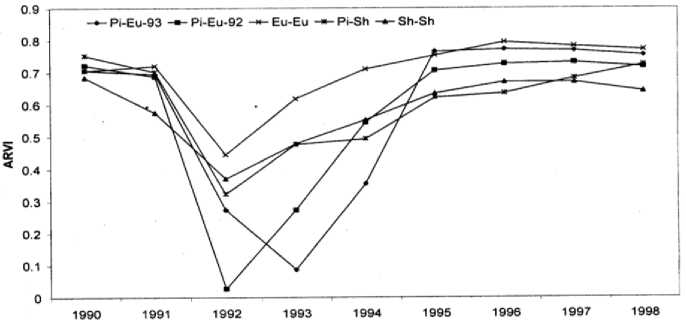
Рис. 1. Кривые временного изменения значений ARVI применительно к пяти тестовым участкам. Принятые обозначения:

Sh — Sh - кустарники; Eu — Eu - эвкалипты; ( Pi — Sh ) - Бук и кустарник; ( Pi — Eu ) - Бук и эвкалипт.

На рис. 1 приведено временное изменение величины ARVI применительно к тестовым участкам, где были организованы пожары в течение конца 1991 и начала 1992 г. Как видно из графиков представленных на рис. 1 вегетационный индекс ARVI в целом может быть использован для оценки общего состояния роста вегетации в зонах прошедших лесных пожаров. Одним из основных показателей роста и состояния лесонасаждений является его фракционный показатель. В общем случае фракционный показатель определяет степень заполнения фиксированного участка вегетацией.

Для контроля состояния роста равномерно посаженных вегетационных участков могут быть использованы однопараметрические и двухпараметрические методы. К однопараметрическим методам можно отнести нахождение фракционного показателя f при известном значении NDVI для заданного типа вегетации. В качестве примера на рис. 2 приведена зависимость NDVI от фракционного показателя покрытия участка растительностью [2].

К двухпараметрическим методам определения фракционного показателя вегетации в качестве примера можно привести способ определения f по разности величин NDVI и ARVI .

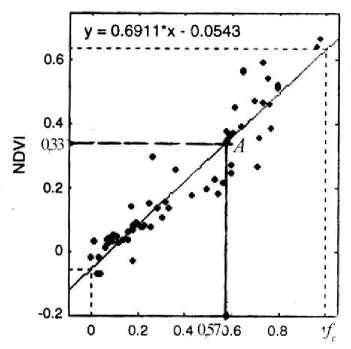
Рис. 2. Использование линейной регрессионной зависимости NDVI от f для определения f при заданной величине NDVI (при NDVI =0,33 определяется точка A и ее абсцисса определяет f = 0,57 ).

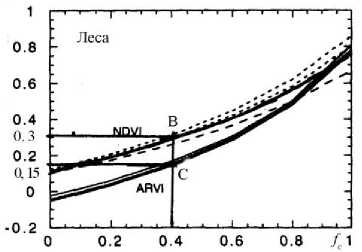
Рис. 3. Использование заданных графиков зависимости NDVI и ARVI [3], для вычисления f по разности NDVI – ARVI .

На рис. 3 показаны графики зависимости NDVI и

ARVI от фракционного показателя f . Как видно из рис. 3 имеет место однозначная зависимость разности NDVI–ARVI от фракционного показателя f . Следовательно, определив разность этих индексов можно определить f по заданным кривым.

Покажем, что степень фракционности равномерно посаженных полей растительности также может быть проконтролирован с использованием модели Гутмана. Хорошо известно, что [4] согласно модели Гутмана изображение получаемое с помощью бортовой аппаратуры содержит мозаичные пиксели. Каждый пиксель имеет мозаичную структуру. Спектральная информация, получаемая с пикселя составлен из вегетационной и почвенной спектральной информации. Одно и то же значение NDVI может быть получен при различных суб-пиксельных структурах.

Согласно модели, Гутмана, для участка с полностью однородной вегетацией верно модифицированный закон Бер

NDVI = NDVI - ( NDVI„ - NDVI₀ ) exp ( - kL_g ) ,(1) где L - индекс листовой площади; k - коэффициент экстинкции; NDVI и NDVI - сигналы, получаемые от голой почвы и полностью плотной вегетации.

Следует отметить, что модель (1) в целом пригодна для оценки однородно посаженных лесных плантаций. Однако, прямое использование модели (1) для однозначного определения фракционности для различных типов растительности затруднительно, так как показатель k оказывается зависимым не только от показателя фракционности, но и от типа рассматриваемой растительности. В качестве примера на рис. 4 приведены графики экспоненциальной зависимости NDVI от LAI для шести типов растительности. Как видно из приведенных на рис. 4 кривых кривизна линии зависимости NDVI от LAI зависит как от типа растительности, так и от предыстории развития растительности (то есть от исходной величины LAI ).

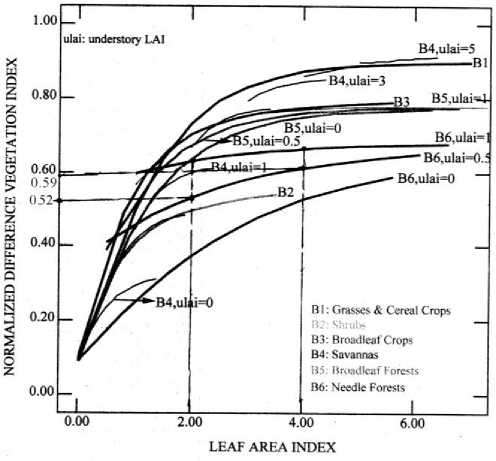
Рис. 4. Кривые экспоненциальной зависимости NDVI от LAI для разных типов растительности при различных исходных значениях LAI .

Очевидно, что данный факт вносит неоднозначность в определения величины k в формуле (1). С учетом вышесказанного далее, в настоящей статье мы предложим некоторую модификацию модели (1) путем введения коэффициента обобщенной калибровки и (2) покажем путь вычисления этого коэффициента.

Выражение (1) запишем в следующем виде

( VDVI — NDVI ) = С - ( NDVI„ — NDVI ₀) exp ( kL ) (2)

где С – коэффициент обобщенной калибровки.

Общеизвестно     [5],     что     теоретически

NDVI, = 1; NDVIq = — 1 . Следовательно, выражение (2) принимает следующий вид

1 — NDVI = C - 2 - exp ( — kL ) . (3)

В целях обобщенной калибровки проводимых дистанционных измерений следует определить коэффициент C , который будет верна для случаев равенства индекса LAI к L и p _- L . Возведение (3) в степень p дает

( 1 — NDVI_l ) ^p = C p - 2 ^p - exp ( — pkL ) (4) где NDVI_L - измеренное значение NDVI при LAI = L .

Далее, запишем уравнение (4) для случая LAI = p - L . Имеем равенство коэффициента

( 1 — NDVI _{p £}) = C - 2 - exp ( — pkL ) ,  (5)

где NDVI - измеренное значение NDVI при

LAI -pL'1

Поделив выражение (4) на выражении (5) получим

( 1 — NDVI_l ) ^p = C p — 1 2 p — 1 .      (6)

( 1 — NDVI pL )

Из выражения (6) окончательно находим

_  1     I ( 1 — NDVIl ) ^p

L .

C = — - ^{p 1} 7------------ v

2   \ ( 1 — NDVI pL )

Например, при p = 2 имеем

Функциональное предназначение дополнительно вводимого параметра заключается в возможности некоторой разгрузки показателя k , в том понимании, что показатель C не зависящая от k может характеризовать степень фракционности растительности, в то время как показатель k будет характеризировать растительности.

В заключение сформулируем основные выводы и положения проведенного исследования:

• 1.    Приведен краткий обзор методов дистанционного контроля роста равномерно посаженных растительных плантаций.

• 2.    Показана возможность модификации известной модели Гутмана, определяющего взаимосвязь между LAI и NDVI для равномерно посаженных растительностей.

• 3.    Предложено введение в модель Гутмана дополнительного мультипликативного показателя независящего от крутизны экспоненциальной зависимости NDVI и LAI .