Усталостная чувствительность стеклопластиков в условиях пропорционального циклического растяжения с кручением

ВЕСТНИК ПНИПУ. МЕХАНИКА № 6, 2023PNRPU MECHANICS BULLETIN

Использование современных полимерных композиционных материалов вместо традиционных металлов и сплавов в ответственных деталях и узлах конструкций позволяет решать проблему снижения массы при сохранении высокого уровня физико-механических характеристик, что наиболее актуально для гражданской авиации, судостроения, строительства, автомобилестроения, а также нефтегазохимической промышленности [1–10]. При этом важно учитывать, что каждое динамическое, циклическое либо вибрационное воздействие, даже малой интенсивности и продолжительности, может привести к существенному изменению механических характеристик материала, что, в свою очередь, вызывает значительное снижение ресурса изделий из композитов. Данные особенности должны быть учтены при проектировании конструкций.

Большое число работ посвящено изучению закономерностей изменения прочностных и жесткостных характеристик полимерных композиционных материалов, подверженных одноосным циклическим воздействиям [11– 15]. Однако в подверженных циклическим воздействиям конструкциях чаще всего реализуется сложное напряженно-деформированное состояние, характеризующееся различными соотношениями амплитуд компонент тензора напряжений [16–20], углами сдвига фаз между модами нагружения [21], соотношениями частот [21], средними напряжениями в цикле [22–25]. Следовательно, необходимо исследовать влияние поврежденности, накопленной вследствие многоосной усталости, на изменение механических характеристик материала.

Современные испытательные системы позволяют реализовывать многоосное циклическое воздействие путем нагружения крестообразных образцов по двум ортогональным осям, растяжения трубчатых образцов при наличии внутреннего давления, совместного кручения с изгибом трубчатых образцов, а также совместного растяжения – сжатия с кручением [26–37]. Результаты исследований, посвященных изучению деградации механических характеристик конструкционных полимерных композитов в условиях двухосных циклических воздействий, представлены в работах [38–40]. Отмечена проблема надежного крепления трубчатых образцов в захватах испытательных систем [41].

Полученные экспериментально зависимости остаточных прочностных и жесткостных характеристик материала от продолжительности предварительного циклического воздействия представимы в виде так называемых диаграмм усталостной чувствительности [42–45]. В некоторых случаях кривая усталостной чувствительности представляется в виде зависимости динамического модуля упругости от числа циклов воздействия в относительных координатах [42; 45]. Как правило, получаемые диаграммы имеют три характерные стадии: I – стадия инициации, характеризующаяся быстрым снижением остаточной прочности и жесткости при малой продолжительности циклического воздействия; II – протяженная

(≈60–85 % от долговечности) стадия стабилизации, соответствующая медленному снижению остаточных механических характеристик; III – стадия обострения, на которой происходит резкое снижение механических характеристик, приводящее к макроразрушению образца. Границы перехода между данными стадиями могут быть определены по точкам, в которых угол наклона касательной к кривой усталостной чувствительности достигает значения, характерного для данного класса материала [44].

Существуют различные модели, позволяющие аппроксимировать полученные экспериментально диаграммы усталостной чувствительности. В частности, одна из широко используемых моделей была предложена Мао и Махадеваном [46]; в ней аппроксимация проводится двумя степенными функциями. Авторами данной работы было отмечено, что вид кривых усталостной чувствительности напоминает интегральные функции распределения вероятности. На основе этого были разработаны две модели, основанные на использовании закона распределения Вейбулла и бета-распределения [42]. Верификация перечисленных трех моделей была проведена в работах [45; 47], наилучшей описательной способностью обладала аппроксимация, соответствующая интегральной функции распределения вероятности Вейбулла.

Данная работа посвящена исследованию закономерностей деградации жесткостных характеристик композитных трубок, полученных методом непрерывной продольно-поперечной намотки, по мере накопления повреждений вследствие двухосного пропорционального циклического растяжения с кручением. Целью работы является получение новых экспериментальных данных и верификация ранее разработанной модели усталостной чувствительности с выявлением связи между параметрами аппроксимации и видом сложного напряженного состояния в цикле нагружения.

1.    Методика проведения испытаний

Для проведения экспериментальных исследований были подготовлены тонкостенные стеклопластиковые трубчатые образцы, полученные методом непрерывной продольно-поперечной намотки, на основе стекловолокна ЕС 1200 текс и эпоксидной смолы KER 828 холодного отверждения. Рассмотрены два варианта угла намотки: 80° и 85°. Длина образцов составляла 140 мм при длине рабочей части L ≈ 60 мм, внутренний диаметр d = 25,0 мм для образцов с углом намотки 80° и d = 25,4 мм – с углом 85°, наружный диаметр D ≈ 30 мм.

Испытания образцов проведены с использованием сервогидравлической системы Instron 8802 (максимальная нагрузка 100 кН, максимальный крутящий момент 1000 Н^м), оснащенной контроллером FastTrack и программным обеспечением WaveMatrix. Образцы устанавливались в цанговые захваты, для предотвращения смятия торцов на всю длину захватных частей были установлены цилиндрические стальные заглушки. Изображения испытательной системы, цанговых захватов и стальной заглушки приведены на рис. 1. При установке образца давление в контуре сервогидравлических захватов постепенно повышалось с 50 до 200 бар. С целью предотвращения деформирования образцов в процессе закрепления значения осевой нагрузки и крутящего момента удерживались на нулевом уровне.

Рис. 1. Фотографии (слева направо): испытательной системы Instron 8802, цангового захвата, стальной заглушки

Fig. 1. Photos of (from left to right): Instron 8802 testing system, collet grip, cylindrical steel plug

Рассмотрены методические аспекты крепления образцов в цанговых захватах для предотвращения проскальзывания. Отработаны три варианта подготовки захватных частей: 1 – без специальной подготовки; 2 – установка прокладки в виде наждачной бумаги; 3 – вклеивание в алюминиевые тонкостенные гильзы. Использовался эпоксидный клей марки ЦМК-5, после вклеивания образцы с гильзами выдерживались в печи при температуре 80 °С в течение 3 ч.

Проведены испытания образцов на квазистатические растяжение и кручение. Скорость перемещения траверсы испытательной системы в процессе растяжения составляла 2 мм/мин, скорость вращения при кручении – 20 °/мин. Выявлено, что отсутствие подготовки захватной части приводило к проскальзыванию и разрушению образца под захватом испытательной системы. Наждачная бумага позволила избежать проскальзывания при кручении, разрушение происходило в рабочей части, однако при растяжении происходило проскальзывание и разрушение образца на границе цанги. Вклеивание образцов в алюминиевые гильзы позволило избежать проскальзывания образцов во время испытаний. Отмечено, что при использовании гильз с толщиной стенки менее 1 мм разрушение происходило на границе цанги, с толщиной стенки 1,5 мм – в рабочей части образца. В связи с этим рекомендуется при проведении испытаний композитных трубок вклеивать их в металлические гильзы с толщиной стенки не менее 1,5 мм. Фотографии разрушенных образцов с различными вариантами подготовки захватных частей представлены на рис. 2.

Скорость перемещения подвижного захвата испытательной системы при квазистатическом испытании на одноосное растяжение (Р) составляла 2 мм/мин. Режиму нагружения «Пропорциональный 1» (ПЦ1) соответствовала скорость перемещения траверсы 1 мм/мин, режиму

«Пропорциональный 2» (ПЦ2) – 2 мм/мин, режиму «Пропорциональный 3» (ПЦ3) – 4 мм/мин. В испытании на кручение (К), а также во всех режимах пропорционального нагружения скорость вращения захвата составляла 20 °/мин. В процессе квазистатических испытаний проводилась запись перемещения u , осевой нагрузки P , угла закручивания φ и крутящего момента M . С их помощью проводилось построение диаграмм деформирования в виде зависимости нормальных напряжений σ от осевой деформации ε и касательных напряжений τ от угла сдвига γ, которые рассчитывались по формулам:

4 P       u 16 DM ф D

ст =               ; e = ; т =               ; y =            . (1)

n(D2 -d2)     L     n(D4 -d4)     2L(1 + e) 1 ’

Рис. 2. Фотографии разрушенных образцов (слева направо): без предварительной подготовки захватной части; с наждачной бумагой; с алюминиевыми гильзами, толщина стенки менее

1 мм; с алюминиевыми гильзами, толщина стенки ≈1,5 мм

Fig. 2. Photos of fractured samples, which gripping parts were (from left to right): without a preliminary preparation; wrapped in sandpaper; glued into aluminum sleeves less than 1 mm thick; glued into aluminum sleeves ≈1.5 mm thick

Для каждого режима нагружения определялись средние значения максимальных нормальных напряжений σ max и касательных напряжений τ max . Амплитуды и средние значения нормальных и касательных напряжений подбирались таким образом, чтобы максимальные значения напряжений в цикле соответствовали половине σ max и τ max , а коэффициент асимметрии был равен 0,1. Частота нагружения во всех случаях составляла 1 Гц. Для каждого из режимов нагружения было испытано по 2–3 образца. В процессе циклического нагружения записывались пиковые значения нагрузки, перемещения, угла закручивания и крутящего момента каждый первый, десятый и сотый цикл. Полученные данные были использованы для вычисления динамических модулей упругости E ′ и G ′ в N -м цикле:

E '_ max min .

u max - u min п ( D 2 - d 2 )’

M max - M min     32 L

G =-- 7----------\.

^ф max ^-ф min " ( D 4 - d 4 )

Если обозначить динамический модуль Юнга за первый цикл как E0, динамический модуль сдвига за первый цикл как G0, то можно рассчитать коэффициенты усталостной чувствительности KE и KG, отражающие падение жесткости материала по мере накопления усталостных повреждений, а также соответствующее им относительное значение предварительного циклического воздействия n:

'_E = E ; k_g

EG E 0

G ' N

—; n = —. G 0 N 0

Получены экспериментально зависимости K E ( n ) и K G ( n ) аппроксимируются разработанной авторами ранее моделью, в которой используется интегральная функция распределения вероятности Вейбулла. Границы стадий накопления повреждений определяются по точкам, где скорость роста поврежденности ω′ E превышает пороговое значение (0,3 для графиков снижения динамического модуля Юнга и 0,5 для графиков снижения динамического модуля сдвига). Зависимости K E ( n ) и ω′ E ( n ) имеют вид

K_E _ 1 -X _E ( -In ( 1 - n ) ) k E ;

to '_E = — (-ln ( 1 - n ) )^K E ¹       .

E КE (          )!     1 - n

Параметры модели κ E и λ E определяют форму и масштаб кривой усталостной чувствительности соответственно и определяются численно методом наименьших квадратов.

Представленная методика проведения испытаний, подготовки захватных частей стеклопластиковых тонкостенных трубчатых образцов и интерпретации получаемых экспериментальных данных позволяют исследовать закономерности изменения остаточных механических характеристик полимерных композитов в условиях двухосных циклических воздействий.

2.    Результаты статических испытаний

В результате проведения квазистатических испытаний на одноосное растяжение, кручение и пропорциональное растяжение с кручением стеклопластиковых трубчатых образцов с углами намотки 80° и 85° получены зависимости нагрузки от перемещения и крутящего момента от угла закручивания. На их основе с использованием формулы (1) построены диаграммы деформирования при растяжении и при сдвиге для различных режимов нагружения (рис. 3).

При одноосном растяжении образцов с углом намотки 85° поведение материала является практически упругохрупким. Со снижением угла намотки до 80° происходит качественное изменение характера деформирования при растяжении, появляется протяженная стадия неупругого упрочнения. При пропорциональном нагружении на диаграммах деформирования при растяжении можно отметить наличие закритической стадии деформирования [48], для образцов с углом намотки 80° она является более протяженной. При одноосном кручении для обеих групп образцов также выявлено наличие ниспадающего участка диаграммы деформирования. Обнаружено увеличение максимального значения нормальных напряжений σmax и снижение максимального значения касательных напряжений τmax с ростом скорости перемещения траверсы. Можно сделать вывод о значительной чувствительности материала к сложному напряженному состоянию для обоих углов намотки.

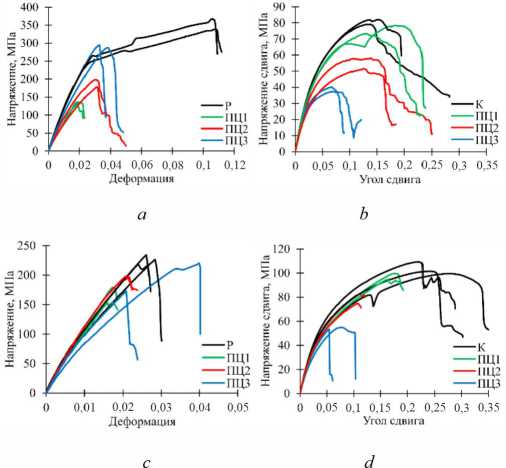
Рис. 3. Диаграммы деформирования: a , b – для образцов с углом намотки 80°, c , d – для образцов с углом намотки 85°, a , c – при растяжении, b , d – при сдвиге

Fig. 3. Stress–strain curves: a , b – for the samples with winding angle of 80°, c , d – for the samples with winding angle of 85°, a , c – during tension, b , d during torsion

Полученные экспериментально максимальные значения касательных и нормальных напряжений могут быть аппроксимированы выражением, задающим критерий разрушения, аналогичный критерию Хашина для разрушения матрицы при растяжении:

□       I     I T I max । max

CT,         j                      J

^ 0max ) V ^T 0max )

= 1.

Здесь σ 0max и τ 0max соответствуют случаям разрушения при одноосном растяжении и при чистом сдвиге. Данные параметры были подобраны численно методом наименьших квадратов и составили: σ 0max =342,5 МПа и τ 0max =79,3 МПа для угла намотки 80° и σ 0max =242,0 МПа и τ 0max =113,8 МПа для угла намотки 85°. На рис. 4 приведены полученные экспериментально максимальные значения нормальных и касательных напряжений, их средние значения для различных режимов нагружения, а также аппроксимация по формуле (5).

Отмечено, что используемая аппроксимация хорошо соответствует экспериментальным данным. Выявлено, что рост угла намотки с 80° до 85° приводит к существенному изменению параметров σ 0max (уменьшение на 29 %)

и τ 0max (увеличение на 44 %). Сделан вывод о значительном влиянии схемы на прочность рассматриваемых композитов. Кроме этого, представляется целесообразной модификация выражения (5) для учета угла намотки [49] и улучшения соответствия получаемых поверхностей прочности экспериментальным данным.

c

2 200

I 150

50 0

■%<

о

Эксперимент ^

Среднее          '

- Аппроксимация xt

--1----1----1----1----1----1----1—^—I

0 10 20 30 40 50 60 70 80 90

Tmax, МПа

C3

5 150

i wo b

x Эксперимент '

о Среднее             ,

---Аппроксимация      I -------1---------1--------- 1--------- 1-------- *e-x^-

0   20 40 60 80 100 120

Tmax, МПа

b

Рис. 4. Максимальные значения напряжений при пропорциональном двухосном нагружении и их аппроксимация: a – для образцов с углом намотки 80°; b – с углом намотки 85°

Fig. 4. Maximum stress values under proportional biaxial loading and data approximation: a – for the samples with winding angle of 80°; b – with winding angle of 85°

3.    Результаты усталостных испытаний

В результате проведения усталостных испытаний получены значения долговечности стеклопластиковых трубчатых образцов с различными схемами армирования при различных вариантах пропорционального циклического воздействия. Данные приведены в таблице.

Результаты усталостных испытаний (средние значения долговечности)

Fatigue tests results (average durability values)

Угол намотки	Усталостная долговечность N , циклов
	Режим нагружения
	Р	К	ПЦ1	ПЦ2	ПЦ3
80°	7598 ± 1270	97133 ± 27930	2325 ± 552	12502 ± 1116	4347 ± 1652
85°	29519 ±	21456 ±	2466 ±	13429 ±	17650 ±
	20848	14765	1374	6360	1481

Во всех случаях наблюдались значительные коэффициенты вариации значений долговечности. Выявлено, что при угле намотки 85° долговечность при одноосном циклическом растяжении и циклическом кручении является схожей, однако при снижении угла намотки до 80° происходит значительное снижение долговечности при циклическом растяжении и повышение долговечности при кручении. Отмечено существенное влияние вида напряженного состояния в цикле нагружения на долговечность. Выявлено, что наиболее опасным вариантом циклического нагружения для обеих групп образцов являлся режим «Пропорциональный 1», при этом изменение угла намотки слабо повлияло на значение долговечности. Обнаружено, что связь долговечности с величиной соотношения между амплитудами касательной и нормальной составляющих тензора напряжений является немонотонной. Требуется проведение дальнейших испытаний для уточнения характера данной зависимости.

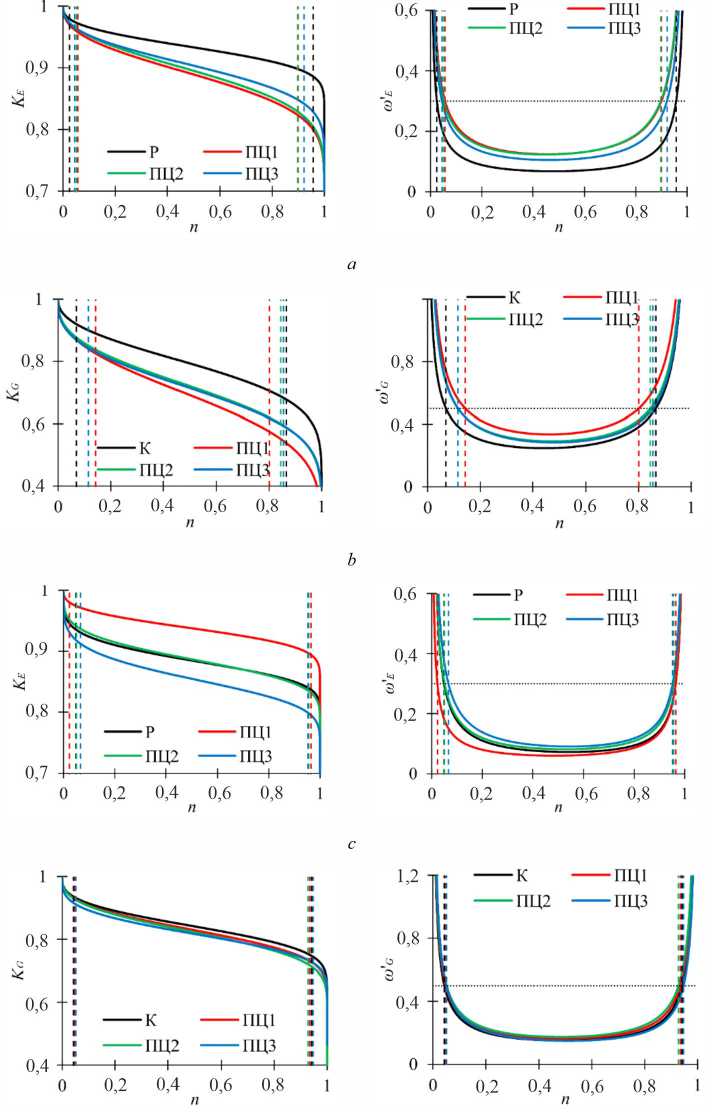
Для каждого циклического испытания проведена обработка полученных экспериментально в соответствии с формулами (2)–(4) зависимостей коэффициентов усталостной чувствительности от относительного значения предварительного циклического воздействия. Пример полученных кривых усталостной чувствительности для образца с углом намотки 80° при циклическом нагружении в режиме «Пропорциональный 2», а также соответствующих им графиков скорости роста поврежденности представлен на рис. 5. На рисунке вертикальные пунктирные линии соответствуют границам стадий накопления повреждений, горизонтальная пунктирная линия – величине скорости роста поврежденности, при которой происходит смена стадии.

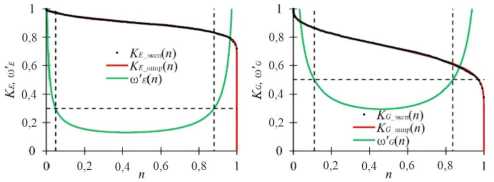
a                                 b

Рис. 5. Пример кривых усталостной чувствительности и соответствующих функций скорости роста поврежденности: a – для динамического модуля Юнга; b – для модуля сдвига

Fig. 5. Example of fatigue sensitivity curves and corresponding damage function growth rate: a – for the dynamic Young’s modulus; b – for the shear modulus

Во всех случаях аппроксимации обладали высокой описательной способностью несмотря на наличие только двух параметров, коэффициент детерминации R ² был не ниже 0,955. В связи с этим сделан вывод о рациональности использования предложенной модели для анализа характера изменения жесткостных характеристик композитов по мере накопления усталостных повреждений.

Связь между определяемыми параметрами аппроксимации и видом сложного напряженного состояния может быть выражена в виде зависимостей параметров κ E и λ E от величины η, рассчитываемой по формуле:

П = arctan

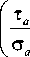
^ Оти

Tn„

0max

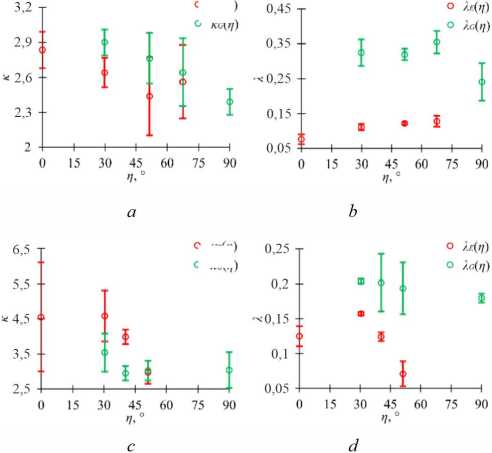
где σ a и τ a – амплитуды нормальных и касательных напряжений в цикле. На рис. 6 продемонстрированы полученные зависимости κ E (η) и λ E (η).

° К^)

0 кад>

0 Мч)

Рис. 6. Зависимости параметров аппроксимации от вида напряженного состояния: a , c – κ(η); b , d – λ(η); a , b – угол намотки 80°; c , d – угол намотки 85°

Fig. 6. Dependences of approximation parameters of stress state: a , c – κ(η); b , d – λ(η); a , b winding angle of 80°; c , d winding angle of 85°

Выявлено, что коэффициент вариации значений параметров аппроксимации для одного режима нагружения и одного угла намотки находится в диапазоне 3–26 % и лишь в одном случае достигает 34 %. Это подтверждает, что параметры κ и λ достаточно точно отражают чувствительность композитов к усталости, следовательно, могут быть использованы для определения механического поведения материала в условиях циклического нагружения.

Отмечено, что в некоторых случаях параметры аппроксимации кривых усталостной чувствительности слабо зависят от вида сложного напряженного состояния (например, κ G (η) и λ G (η) для образцов с углом намотки 85°). В других случаях полученные зависимости являются монотонно убывающими (для образцов с углом намотки 80°) либо возрастающими (κ G (η) и λ E (η) для образцов с углом намотки 85° соответственно). Также присутствуют немонотонные зависимости (λ E (η) для образцов с углом намотки 85°). На основе этого можно сделать вывод о различном характере влияния вида напряженного состояния при пропорциональных циклических воздействиях на параметры аппроксимаций кривых усталостной чувствительности. Необходимо проведение дальнейших исследований для уточнения полученных зависимостей от вида сложного напряженного состояния в цикле нагружения.

На рис. 7 представлены построенные для средних значений параметров аппроксимации в каждом режиме нагружения кривые усталостной чувствительности и соответствующие графики скорости роста поврежденности с границами стадий накопления повреждений.

Для сравнения различных режимов циклического воздействия целесообразно ввести такой параметр, как среднюю скорость снижения коэффициента усталостной чувствительности на стадии стабилизации:

KE ( n1 )- KE ( n 2 )V E = —--—.

n 2 - n

Здесь n 1 и n 2 – левая и правая граница стадии стабилизации, соответственно.

d

Рис. 7. Осредненные кривые усталостной чувствительности (слева) и соответствующие графики скорости роста поврежденности (справа): a – K E ( n ), угол намотки 80°; b – K G ( n ), угол намотки 80°; c – K E ( n ), угол намотки 85°; d – K G ( n ), угол намотки 85°

Fig. 7. Average fatigue sensitivity curves (left side) and corresponding damage growth rate function (right side): a – K E ( n ), winding angle of 80°; b – K G ( n ), winding angle of 80°; c – K E ( n ), winding angle of 85°; d – K G ( n ), winding angle of 85°

Выявлено, что для образцов с углом намотки 80° по мере роста касательной составляющей тензора напряжений наблюдается постепенное повышение скорости снижения динамического модуля Юнга (параметр ψ E вырос с 0,10 до 0,16 для режимов одноосного растяжения и «Пропорциональный 1»), сопровождающееся уменьшением продолжительности стадии стабилизации (на ≈10 %). Иные результаты наблюдались для динамического модуля сдвига: наименьшая скорость снижения коэффициента усталостной чувствительности выявлена для чистого сдвига (ψ G =0,305), наибольшая – для режима нагружения «Пропорциональный 1» (ψ G =0,380), протяженность стадии стабилизации снизилась на ≈17 %. Кривые усталостной чувствительности для режимов нагружения «Пропорциональный 2» и «Пропорциональный 3» заняли промежуточное положение. Данная особенность может быть связана с более низкой долговечностью образцов в режиме «Пропорциональный 1» и иным характером накопления усталостных повреждений.

Повышение угла намотки с 80° до 85° привело к изменению характера влияния вида сложного напряженного состояния на вид кривых усталостной чувствительности. Так, наибольшая скорость снижения динамического модуля Юнга соответствовала режиму нагружения «Пропорциональный 3», наименьшая – режиму «Пропорциональный 1» (параметр ψ E составил 0,127 до 0,091 соответственно). Протяженность стадии стабилизации изменилась при этом на ≈6 %. Кривые усталостной чувствительности при одноосном растяжении и режиме нагружения «Пропорциональный 2» заняли промежуточное положение. Кривые усталостной чувствительности, отражающие изменение динамического модуля сдвига, во всех случаях оказались близкими: параметр ψ G составил 0,204–0,234, протяженность стадии стабилизации – около 0,88. Отмечено, что изменение угла намотки привело к снижению скорости изменения динамического модуля сдвига для всех режимов нагружения, при этом характер снижения динамического модуля Юнга остался схожим.

На основе вышеизложенного можно сделать вывод о значительном влиянии соотношения между нормаль- ными и касательными составляющими тензора напряжений при пропорциональном нагружении, а также угла намотки на усталостную чувствительность рассматриваемых композитных трубчатых образцов. Целесообразным является проведение дальнейших исследований для уточнения характера выявленных закономерностей.